Финансовые соглашения предусматривают разные способы начисления процентов. При этом обычно оговаривается номинальная годовая процентная ставка. Но эта ставка не отражает эффективности сделки и не может быть использована для сопоставлений. Для обеспечения сравнительного анализа эффективности таких соглашений выбирается показатель универсальный для любой схемы начисления процентов, который называется – эффективная годовая процентная ставка (ref).
Пусть задан исходный капитал PV, годовая (номинальная) процентная ставка r и число начислений сложных процентов - m. Наращенный капитал при таких исходных данных обозначим FV. Требуется найти такую годовую ставку ref которая обеспечит такое же наращение, как и исходная схема, но при однократном начислении процентов за базовый временной период.
Математически это приводит к уравнению
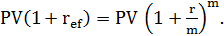 (3.8)
(3.8)
Откуда следует
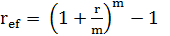 (3.9)
(3.9)
В финансовых соглашениях можно указывать эффективную и номинальную ставки, так как обе дают один и тот же результат наращения. В США применяют номинальную ставку, а в европейских странах применяют эффективную ставку и расчет ведут по формуле
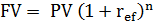 (3.10)
(3.10)
где n-срок начисления процентов.
Из формулы (3.9) следует выражение для вычисления номинальной ставки r при известной эффективной ставки ref и числе m начислений процентов в год
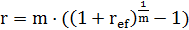 (3.11)
(3.11)
Если две номинальные ставки определяют одну и ту же эффективную ставку, то они называются эквивалентными.
Рассмотренный подход не единственный для определения эффективной ставки. Например, при изменении условий начисления процентов (целые года – сложный процент, внутригодовые начисления – простой процент), можно предложить схему определения ref не использующую явным образом номинальную ставку. Если известен первоначальный капитал PV и наращенный капитал FV за время n.Тогда из уравнения (10), следует
 (3.12)
(3.12)
! Пример. Эффективная и номинальная ставки
Предприниматель может получить ссуду а) либо на условиях ежемесячного начисления процентов из расчета 26% годовых, б) либо на условиях полугодового начисления процентов из расчета 27% годовых. Какой вариант более предпочтительнее.
Решение.
Воспользуемся формулой (3.9) и определим ref для вариантов а) и б):
a)
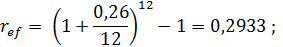
б)
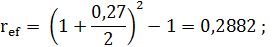
Вариант б), для предпринимателя, более выгоден.
Пример.
Определить номинальную ставку r, если эффективная ставка равна 18% и сложные проценты начисляются ежемесячно
Решение.
Из формулы (11) следует
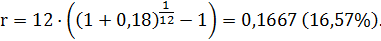
Пример.
Каковы будут эквивалентные номинальные годовые процентные ставки с начислениями по полугодиям и ежеквартально, если ref = 20%.
Решение.
Из формулы (3.11) следует, что рассчитанные ниже номинальные ставки эквивалентны при ref = 20%:
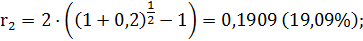
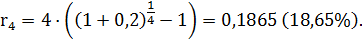
Дата: 2019-04-22, просмотров: 689.