Основой математической модели процесса охлаждения потока перегретого расплава в каналах литниковой системы и в полости формы во время ее заливки являются дифференциальное уравнение теплопереноса и дифференциальные уравнения гидродинамики (уравнение сплошности потока и уравнение движения Навье-Стокса).

В большинстве случаев поток расплава в форме турбулентный, течение в горизонтальном канале в первом приближении стационарно. Следовательно, cкорость (W) потока допустимо рассматривать распределенной однородно по сечению и принять постоянной по длине канала, определяемой гидростатическим напором, в тех случаях, когда режим течения расплава ламинарный, будем иметь в виду среднюю скорость (w) по сечению. Поэтому необходимость в дифференциальном уравнении движения жидкости Навье-Стокса отпадает.

Пусть расплав течет в положительном направлении координатной оси Y в плоскости щели, толщина которой S=2Lk (Lk-половина толщины канала) теплота от потока расплава отводится только в форму в направлении оси X. Скорость w течения расплава постоянна. Тогда время течения расплава до рассматриваемого сечения, отстоящего от начала канала на расстоянии можно выразить через скорость потока.

На основании, что поток охлаждается симметрично интегральная величина теплового потока при течении по каналу запишется через плотность теплового потока, уходящего в форму в соответствии с законом теплопроводности Фурье.

Так как форма в сечении канала прогревается столько времени, сколько течет расплав мимо этого сечения, то распределение температуры в форме в сечении канала можно определить в соответствии с классическим решением:

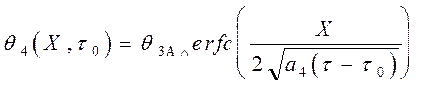         (3.28)      -время течения расплава в канале формы;

-время течения расплава до рассматриваемого сечения канала.  

Здесь в качестве постоянной температуры поверхности формы  принята температура 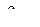 заливки металла. Учитывая малую интенсивность охлаждения и затвердевания металла имеем возможность пренебречь величиной температурного перепада по сечению потока т.е. принять  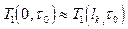  .Тогда интеграл в левой части примет форму:

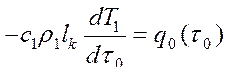                                    (3.29.)

Таким образом , упрощенная математическая модель процесса охлаждения стационарного потока расплава в песчаной форме представляется обыкновенным дифференциальным уравнением с соответствующими начальными условиями.

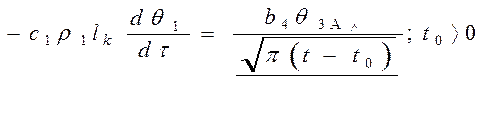                                                     (3.30)

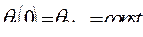
  Если размер канала заменить приведенной толщиной , то температура на носике потока запишется выражением:

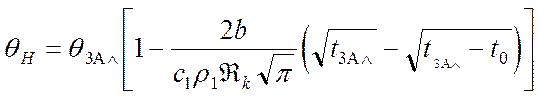              (3.31)  

program lesha; {Программа процесса остывания металла во время заливки }

var Tau1,Tn:Array [1..50] OF Real;

Bf,dTau,Tau,Tauz,Tz,F,L,dV,V0,V,dL,Q,W,R,c:Real;

I,Imax:integer;

F2:Text;

begin { Начало программы }

assign (F2,'e:\TP7\G3661\lesha.rez ');rewrite (F2);

 Bf:=0.16; { Тепловая активность формы Вт**с**0.5/см**2*К }

 Tz:=1550; {Температура заливки }

 {Tn:=           Температура текущего i-того объема}

 Tau:=0;  { Начальное время сек.}

 dTau:=0.04; { Приращение времени сек }

 Q:=50;       { Поступление жидкого металла по канала см*3*сек }

 I:=0;      { Индексное значение }

 F:=1;         { Площадь поперечного сечения канала см*2 }

 L:=30;      {Длина канала см }

 V0:=20;     {Начальный объем канала см*3 }

 V:=0;             {Объем заполненный к текущему моменту времени }

 R:=0.25;    { Приведенная толщина см }

 c:=7.3;        {Объемная теплоемкость металла Дж/см*3*К}

writeln;

writeln(f2,' Н А Ч А Л О С Ч Е Т А ');

WRITELN(f2);

repeat

Tau:=Tau+dTau; I:=I+1; Tau1[I]:=Tau; { Время заполнения текущего объема }

        { Расчет длины заполнения канала }

dL:=(Q*dTau)/F; { Длина заполненная за время dTau }

dV:=dL*F;

w:=Q/F;

V:=V+dV;

     { Расчет температуры на носике потока, времени заполнения

             и числа участков }

Tn[I]:=Tz*(1-((2*Bf)/(sqrt(3.14)*c*R)*(sqrt(Tau)-sqrt(Tau-Tau1[I]))));

writeln (f2,'Tau1[I]=',Tau1[I]:5:2,' Tau=', Tau:3:2,' I=', I:2,' Tn[I]=',Tn[I]:8:3 );

until (V>=V0);

writeln(f2,'конец заполнения канала ');

Tauz:=Tau; { Время заполнения канала }

Imax:=I; {Число участков при последовательном заполнении}

{                                                      }

writeln (f2,'Tauz=',Tauz:6:2,' Imax=',Imax:6);

I:=0;

writeln(f2);

writeln(f2,' Распределение температуры в момент заполнения канала ');

repeat

I:=I+1;

        {Распределение температуры на момент конца

            заполнения формы}

Tn[I]:=Tz*(1-((2*Bf)/(sqrt(3.14)*c*R)*(sqrt(Tauz)-sqrt(Tauz-Tau1[I]))));

write (f2,Tn[i]:5:0);

UNTIL(I>=Imax);

writeln(f2);

close(f2);

end.

Таким образом, интересующая нас температура на носике потока легко расчивается для любого сечения канала, если известно время заливки и температура заливки.