В основе расчета важного технологического параметра, времени заполнения формы жидким металлом лежат основные уравнения гидравлики (см. формулы (3.5) и (3.6)). Линейная скорость металла в наиболее узком сечении литниковой системы определяется по формуле:

V = μ  (2 g h )^1/2 ,                                   (3.16)

где μ   - коэффициент скорости, зависящий от потерь напора; h - высота столба жидкого металла, создающего напор.

Для определения объемного расхода в любом сечении литниковой системы используется следующая зависимость:

                 Q = V f _л =μ f _л (2 gh )^1/2 ,                                      (3.17)

где f _л – площадь наиболее узкого сечения литниковой системы;μкоэффициент расхода.

Для протяженных каналов μ = μ

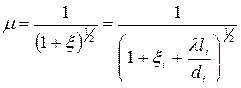 ,                                              (3.18)

где μ - суммарный коэффициент сопротивления литниковой системы; ξ_i - местные потери напора в i – м элементе литниковой системы в результате расширения (сжатия), поворота потока и т.д.; λ - коэффициент потерь на трение о стенки канала (в среднем λ = 0,04); l _i - длина канала; d_i - гидравлический диаметр канала.

Расчет продолжительности заполнения формы при подводе металла сверху

При подводе металла сверху высота напора жидкого металла, создающего напор, в узком сечении остается постоянной в процессе заливки (h = const = h _ст , где h _ст - высота стояка ). Поэтому линейная скорость V и расход не изменяются во времени. Из условий неразрывности потока ( V f _л = h S) можно вычислить скорость подъема металла в форме, имеющей поперечное сечение S:

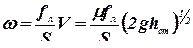 .                             (3.19)

Продолжительность заливки можно определить, вычислив отношение объема формы, равной S * H _ф (S = const), к объему металла, протекающему через сечение f _л :

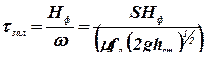 .                                  (3.20)

Скорость подъема металла в форме для отливки сложного сечения (S = const) целесообразно определить с помощью ЭВМ.

Уравнение расхода металла, вытекающего из питателя сечением f _л , запишем в дифференциальной форме:

dQ = μ f _л (2 gH _ст )^1/2 dτ .                                    (3.21)

Соответствующее повышение уровня металла в форме определяется из уравнения баланса в дифференциальной форме:

μf _л (2 gH _ст )^1/2 dτ = Sdf _ф ,                                        (3.22)

где S – горизонтальное сечение формы на уровне h _ф зеркала жидкого металла.

Сечение формы S (h _ф) может быть задано неизменным по высоте S = const ;

- изменяющимся по высоте ступенчатым образом:

S₁ O< h_a< H₁ ;

                                           (3.23)

S ₂ H₁< h_a< H_a ;

- изменяющимся по высоте в соответствии с аналитическим выражением типа  S = S ₀ (1 + K ₁ h_a + K ₂ h_aa ² ...) или другого произвольного вида;

- изменяющимся по высоте в соответствии с таблично заданной функцией.

Расчет продолжительности заполнения формы

При подводе металла сифоном

При подводе металла сифоном высота столба жидкого металла, создающего напор h, меняется во времени и зависит от уровня металла в форме          h_ф( t ): h( t ) = H_ст-h_ф( t ).

По мере заполнения формы, расход Q и скорость поступления металла U уменьшаются.

При постоянном напоре в стояке H_ст количество металла, вытекающего из питателя сечением f, определяется выражением:

                     dQ = m f(2g(H_ст-h_ф))^1/2 d t                              (3.24)

и зависит от противонапора h_ф столба жидкого металла в форме.

Соответствующее повышение уровня металла в форме определяется из уравнения баланса:

Sdh_ф = m f(2g(H_ст-h_ф))^1/2 d t ,                                       (3.25)

где S - горизонтальное сечение формы на уровне h_ф зеркала жидкого металла.

Сечение формы S(h_ф) задается различным образом.