ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ – вид статистического наблюдения, организованный на основе выборки, при котором отбирается часть единиц изучаемой совокупности, по определённым правилам, из общей совокупности единиц. Совокупность единиц, из которых осуществляется отбор, называется ген. совокупностью.

Виды: Простая случайная выборка есть отбор единиц из генеральной совокупности путем случайного отбора, но при условии вероятности выбора любой единицы из генеральной совокупности. Отбор проводится методом жеребьевки или по таблице случайных чисел. Типическая выборка предполагает разделение неоднородной генеральной совокупности на типологические или районированные группы по какому-либо существенному признаку, после чего из каждой группы производится случайный отбор единиц. Для серийной  выборки характерно то, что генеральная совокупность первоначально разбивается на определенные равновеликие или неравновеликие серии, из которых путем случайного отбора отбираются серии и затем внутри отобранных серий проводится сплошное наблюдение. Механическая выборка представляет собой отбор единиц через равные промежутки .При проведении механического отбора генеральная совокупность разбивается на равные по численности группы, из которых затем отбирается по одной единице. Комбинированная выборка основана на сочетании нескольких способов выборки. Многоступенчатая выборка есть образование внутри генеральной совокупности вначале крупных групп единиц, из которых образуются группы, меньшие по объему, и так до тех пор, пока не будут отобраны те группы или отдельные единицы, которые необходимо исследовать.

Выборочный отбор может быть повторным и бесповторным. При повторном отборе вероятность выбора любой единицы не ограничена. При бесповторном отборе выбранная единица в исходную совокупность не возвращается.

Для отобранных единиц рассчитываются обобщенные показатели (средние или относительные) и в дальнейшем результаты выборочного исследования распространяются на всю генеральную совокупность.

Основной задачей при выборочном исследовании является определение ошибок выборки. Принято различать среднюю и предельную ошибки выборки. Для иллюстрации можно предложить расчет ошибки выборки на примере простого случайного отбора.

Следует обратить внимание на то, что под знаком радикала в формулах при бесповторном отборе появляется множитель, где N - численность генеральной совокупности.

Что касается расчета ошибки выборки в других видах выборочного отбора (например, типической и серийной), то необходимо отметить следующее.

Для типической выборки величина стандартной ошибки зависит от точности определения групповых средних. Так, в формуле предельной ошибки типической выборки учитывается средняя из групповых дисперсий,

При серийной выборке величина ошибки выборки зависит не от числа исследуемых единиц, а от числа обследованных серий (s) и от величины межгрупповой дисперсии:

Серийная выборка, как правило, проводится как бесповторная,

Все вышеприведенные формулы применимы для большой выборки. Кроме большой выборки используются так называемые малые выборки (n < 30), которые могут иметь место в случаях нецелесообразности использования больших выборок.

2) при определении доверительных интервалов исследуемого показателя в генеральной совокупности или при нахождении вероятности допуска той или иной ошибки необходимо использовать таблицы вероятности Стьюдента, где Р = S (t, n), при этом Р определяется в зависимости от объема выборки и t.

34.  Расчет коэффициентов роста (падения), опережения (отставания), ускорения (замедления) экономических процессов, их экономический смысл. Темп роста является самым распространенным статистическим показателем, который характеризует отношение данного уровня статистического процесса к предыдущему или начальному, выраженное в процентах. Темпы роста, вычисленные как отношение данного уровня к предыдущему, называются цепными а к начальному – базисными.

Коэффициент опережения – это отношение базисных темпов роста двух динамических рядов за одинаковые отрезки времени Обозначив коэффициент опережения K_оп, базисные коэффициенты роста первого ряда динамики – через К¹ , второго – К¹¹ , Тогда:

К_оп = К¹ / К¹¹ .

Данный коэффициент показывает, во сколько раз будет быстрее расти уровень одного ряда динамики по сравнению с другим .Чтобы знать, что скрывается за каждым процентом прироста, рассчитывается абсолютное значение 1% прироста как отношение абсолютного прироста уровня за интервал времени к темпу прироста за тот же промежуток времени:

Абсолютные приросты показывают скорость изменения уровней ряда в единицу времени. Если они систематически возрастают, то ряд развивается с ускорением

35. Сводка материалов статистического наблюдения как метод агрегирования и представления статистической информации. Задачи и роль сводки и группировки в статистическом исследовании. . Статистическая сводка – комплекс последовательных операций по первичной обработке данных с целью выявления типичных черт и закономерностей, присущих изучаемому явлению . Целью сводки является получение на основе сведенных материалов обобщающих статистических показателей, отражающих сущность социально-экономических явлений и определенные статистические закономерности. Статистическая сводка предполагает:

1-систематизацию и группировку цифровых данных,

2-подсчет соответствующих итогов

3-представление результатов в виде таблиц, графиков.

Группировка – это метод, при котором вся исследуемая совокупность разделяется на группы по какому-то существенному признаку.Принято выделять следующие основные задачи:

- образование социально-экономических типов явлений;

- изучение строения и структуры изучаемых явлений.

Для решения этих задач применяют типологические, структурные и аналитические группировки.

36. Средние величины используются на этапе обработки и обобщения полученных первичных статистических данных. Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности. Средняя арифметическая - самый распространенный вид средней. Она используется, когда расчет осуществляется по несгруппированным статистическим данным, где нужно получить среднее слагаемое. Средняя арифметическая - это такое среднее значение признака, при получении которого сохраняется неизменным общий объем признака в совокупности.

При расчете средних величин отдельные значения признака, который осредняется, могут повторяться, поэтому расчет средней величины производится по сгруппированным данным. В этом случае речь идет об использовании средней арифметической взвешенной. Средняя гармоническая. Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1.Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1:

 гармоническая взвешенная.  Средняя геометрическая. Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста, когда индивидуальные значения признака представлены в виде относительных величин. Средняя квадратическая величина. Основной сферой ее применения является измерение вариации признака. Модой называется значение признака, которое соответствует максимальной точке теоретической кривой распределений.

Медиана (Ме) - это величина, которая соответствует варианту, находящемуся в середине ранжированного ряда.

37. Средний индекс – это индекс, вычисленный как средняя величина из индивидуальных индексов. Средний индекс должен быть тождественен агрегатному индексу. При исчислении средних индексов используются две формы средних: арифметическая и гармоническая.Арифметическая форма индекса используется сводных индексов

количественных показателей, а гармоническая форма индекса – для расчета сводных индексов качественных показателей.

- средний арифметический индекс физического объема находится из предположения, что имеются данные о товарообороте базисного периода (р₀g₀), а также известен индивидуальный индекс физического объема для каждого вида продукции

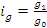, тогда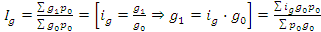

- средний гармонический индекс цен находится из соответствующего агрегатного индекса цен в предположении, что известен товарооборот отчетного периода (р₁g₁), а также индивидуальные индексы цен 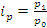, тогда 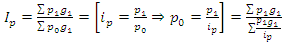- средний гармонический индекс себестоимости продукции определяется если известны затраты на производство продукции в отчетном периоде, а также индивидуальные индексы себестоимости произведенной продукции 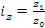, тогда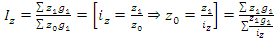

- средний арифметический индекс физического объема определяется из предположения, что известны затраты на производство продукции в базисном периоде и индивидуальные индексы физического объема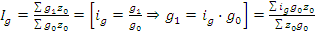

38.Для обобщающей характеристики динамики используются:

средние уровни ряда; средние показатели изменения уровней ряда: Средний абсолютный прирост; Средний коэффициент роста; Средний темп прироста.

Средний уровень интервального ряда рассчитывается по формуле .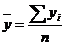
Для нахождения среднего уровня моментного ряда используют среднюю хронологическую: .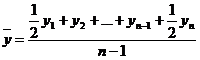
Средний абсолютный прирост рассчитывается в зависимости от исходных данных следующими способами:
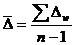или
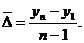
Средний коэффициент роста (снижения):
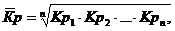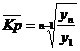или , . Средний темп прироста (снижения): .

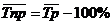39. Статистика как общественная экономическая наука и отрасль практической деятельности. Предмет и метод статистики его особенности. Статистические приемы и методы обработки информации.Статистика – самостоятельная общественная экономическая наука, имеющая свой предмет исследования и специфические предметы анализа.Статистика изучает однородные совокупности. Признаки статистики разделяет на 2 класса:- качественные (атрибутивные)- количественные (в виде цифр) Общим методом познания статистики является диалектический метод, при котором все явления, процессы должны рассматриваться во взаимосвязи и взаимообусловленности. Статистические методы используются комплексно (системно). Это обусловлено сложностью процесса экономико-статистического исследования, состоящего из трёх основных стадий:1. Сбор первичной статистической информации. 2. Статистическая сводка и обработка первичной информации. 3.Обобщение и интерпретация статистической информации.