Выборочная совокупность - часть единиц генеральной совокупности, отобранная в случайном порядке, ее численность обозначается n. Выборочное наблюдение - не сплошное наблюдение, при котором обследованию подвергается оп­ределенная часть единиц изучаемой совокупности, отобранная в случайном порядке.

Основные способы формирования выборочной совокупности : 1)Простая случайная выборка - отбор, при котором единицы отбираются из генеральной совокупности наудачу. 2)Механическая выборка - вид отбора, при котором наблюдению подвергаются единицы, равно отстоящие друг от друга . Если единицы генеральной совокупности располагаются в случайном порядке, не зависящем от изучаемого признака, механическая выборка называется несистематической. Если единицы генеральной совокупности расположены в порядке увеличения или уменьшения изучаемого признака, механическая выборка называется систематической. При механической выборке учитывается шаг отсчета и начало отсчета. Он определяется делением численности генеральной совокупности на объем выборки h = N / n . Начало отсчета - номер единицы, которая должна быть отобрана первой.

3)Типическая выборка применятся для совокупности, не являющейся однородной по изучаемому признаку. При этом генеральную совокупность раз­бивают на однородные группы  по изучаемому признаку. Затем из каждой группы отбирается определенное число единиц.

При пропорциональной выборке из каждой группы отбирают число единиц, пропорциональное удельному весу данной группы в генеральной совокупности. Стандартная ошибка непропорциональной выборки зависит от величины средней из групповых дисперсий .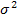

4)Серийная выборка - из генеральной совокупности отбираются не единицы, подлежащие обследованию, а группы единиц. Стандартные ошибки выборки при серийном отборе зависят от величины межсерийной дисперсии, которая оп­ределяется по формуле:

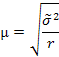
где 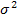^~ - межсерийная дисперсия выборочной совокупности;

r - число отобранных серий. Предельная ошибка серийной выборки:

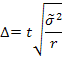
5)Комбинированная выборка - комплексное использование нескольких видов выборки. Величина стандартной ошибки состоит из ошибок на каждой ее ступени и может быть определена как корень квадратный из суммы квадратов ошибок соответствующих выборок. Так, если при комбинированной выборке в сочетании использовались механическая и типическая выборки, то стандартную ошибку можно определить по формуле:

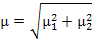
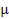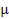Где ₁ и ₂ - стандартные ошибки соответственно механической и типической выборок.