По расходным характеристикам КЭС определим ХОП
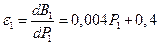 ;
; 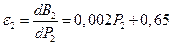 ;
; 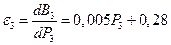 .
.
Составим систему уравнений
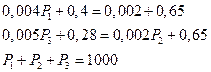
и преобразуем ее к матричному виду
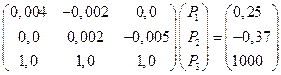 .
.
Решение системы дает следующий результат
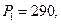
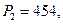
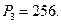
При этом выполняется условие 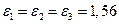 .
.
Оптимальный расход топлива равен 1021,4.
Метод покоординатного спуска
Запишем целевую функцию суммарного расхода топлива системы:
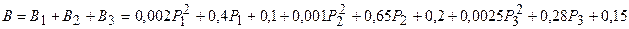 Баланс мощности определяется уравнением
Баланс мощности определяется уравнением 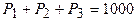 .
.
Мощность 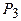 примем в качестве зависимой переменной, выразим её через независимые
примем в качестве зависимой переменной, выразим её через независимые 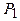 и
и 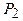 и подставим в уравнение для целевой функции
и подставим в уравнение для целевой функции
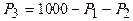 ,
,
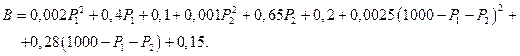
После раскрытия скобок и приведения подобных слагаемых получим целевую функцию суммарного расхода топлива
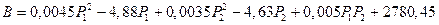 .
.
Найдем минимум данной функции методом покоординатного спуска путем последовательного решения уравнения 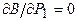 при фиксированном значении
при фиксированном значении 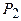 , затем уравнения
, затем уравнения 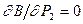 при фиксированном значении Р1.
при фиксированном значении Р1.
Итак, из уравнения 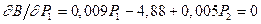 получим
получим
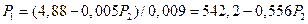 .
.
Аналогично из уравнения 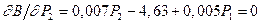 найдем
найдем
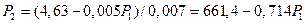
В качестве нулевого приближения примем
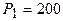 ;
; 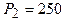 ;
; 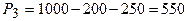 .
.
Значение целевой функции для нулевой итерации 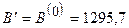 .
.
Результаты расчета приводятся в таблице.
| № | Р1 | Р2 | Р3 | В |
| 0 | 200,0 | 250,0 | 550,0 | 1295,7 |
| 1 | 403,2 | 518,6 | 78,2 | 1130,1 |
| 2 | 253,9 | 373,5 | 372,6 | 1064,6 |
| 3 | 334,5 | 480,2 | 185,3 | 1038,5 |
| 4 | 275,2 | 422,5 | 302,3 | 1028,2 |
| … | ||||
| 13 | 290,4 | 455,5 | 254,1 | 1021,4 |
Ход итерационного процесса показан на рисунке 1.16.
Градиентный метод с оптимальным шагом
Градиент целевой функции B равен
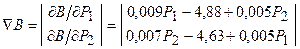 .
.
Примем в качестве нулевого приближения 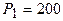 ;
; 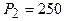 и подставим данные значения в формулы для вектора градиента
и подставим данные значения в формулы для вектора градиента
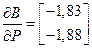 .
.
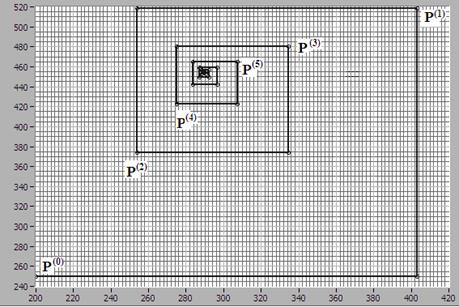
Рисунок 1.16.
Оптимальный шаг в рамках градиентного метода может определяться по результатам одного пробного шага. Выполним пробный шаг длиной t0=100 в направлении антиградиента
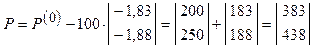 ;
;
Определим градиент в конце пробного шага
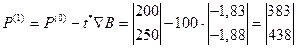 .
.
Определим шаг, близкий к оптимальному, на направлении антиградиента в исходной точке
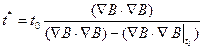 .
.
Скалярные произведения, входящие в выражение, соответственно, равны
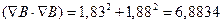 ,
,
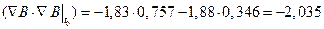 .
.
Оптимальный шаг
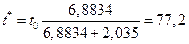 .
.
Рабочий шаг в направлении антиградиента приводит в точку
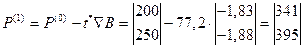
Значение суммарного расхода топлива 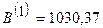 .
.
Аналогично выполняется расчет на следующей итерации.
Обобщенный метод Ньютона (ОМН)
Определим элементы матрицы Гессе для целевой функции B
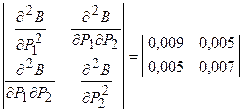 .
.
Определим градиента в точке нулевого приближения 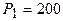 ;
; 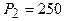 :
:
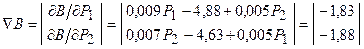 .
.
Решив систему линейных уравнений
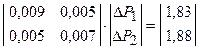 ,
,
получим следующий результат 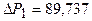 ;
; 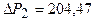 .
.
Новые значения переменных после первой итерации
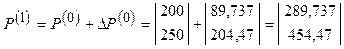 .
.
Суммарный расход топлива составит 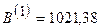 .
.
Значение 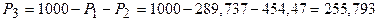 .
.
Как видно, обобщенный метод Ньютона за одну итерацию дает решение, совпадающее с решением, полученным на основе принципа равенства ОПРТ, т.е. ОМН сходится к минимуму за одну итерацию. Оптимальный расход топлива составляет 1021,38.
Метод случайного поиска
В этом методе в текущей точке Р1,Р2, начиная с исходной, рассматривается квадрат с центром в этой точке, и определяется расход топлива в ней B ( P1,P2). Внутри квадрата выбирается новая точка, определяемая следующим образом
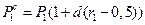 ;
; 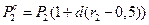 ,
,
где d – сторона квадрата,
r - случайное число с равномерным распределением в диапазоне 0….1.
В новой точке также считается расход топлив и сравнивается с исходным.
Если в новой точке расход оказался меньше расхода в текущей точке, то текущая точка переносится в новую и расчет повторяется.
Результаты расчета приведены в таблице 2.
Таблица 2
| № | Р1 | Р2 | В |
| 0 | 200,0 | 250,0 | 1295,7 |
| 1 | 191,0 | 268,0 | 1284,3 |
| 2 | 198,0 | 305,5 | 1205,6 |
| 3 | 173,5 | 343,2 | 1189,5 |
| 4 | 201,2 | 392,5 | 1090,2 |
| … | |||
| 29 | 289,4 | 454,5 | 1021,4 |
Начальная часть траектории спуска показана на рисунке 1.17
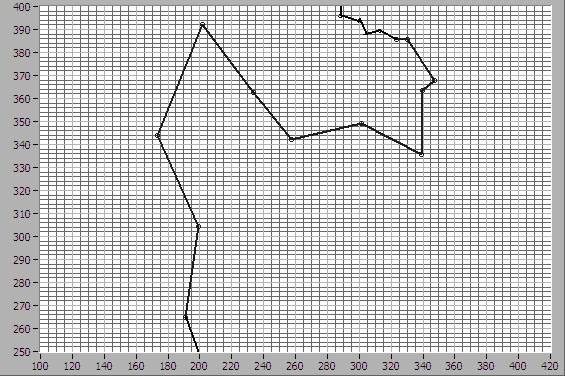
Рисунок 1.17.
Метод прост в реализации алгоритма, но сходится при большом числе итераций.
Дата: 2019-04-23, просмотров: 415.