Сегодня для поиска оптимальных режимов существует много программ, разработанных в свое время в отраслевых НИИ, учебных институтах и службах РЭУ. Они предназначались для  оптимизации путем  решения частные задачи, а также задачи комплексной оптимизации. Рассмотрим алгоритм оптимального  распределения активной мощности для суточного графика по методу относительных приростов.

Математическая модель уже рассматривалась и приведена ниже:

;

;        ;

;     ;

; ; .

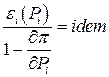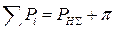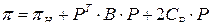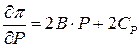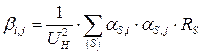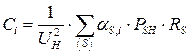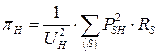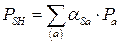Блок- схема алгоритма приведена на рисунке 1.48.

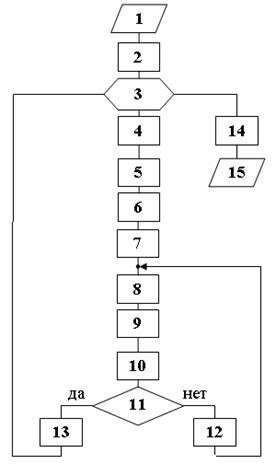
Рисунок 1.48

Блоки выполняют следующие функции:

1. Ввод информации (исходные данные).

2. Определение b _{i , j} матрицы B.

3. Цикл по ступеням суточного графика.

4. Определение P_a ( t ) по графикам нагрузок.

5. Определение P_{SH .}

6. Расчет p _Н и C_i.

7. Исходное приближение мощностей станций P ₀.

8. Определение 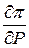 и p.

9. Суммарная нагрузка ЭС .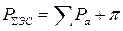

10. Определение оптимальных мощностей станций  P ₁ при фиксированных 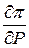 и .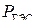

11. Проверка условия для всех станций .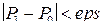

12. Замена P ₀ = P ₁ .

13. Печать и запоминание результата для ступени графика.

14. Представление обобщенных результатов за сутки.

15. Останов.

Оптимизация надежности

Надежность определяется техническим состоянием оборудования и случайными аварийными событиями и изменением нагрузки потребителей.

Уровень надежности является экономической категорией, так как связан с затратами на повышение надежности и сокращением при этом затрат у потребителя при потере питания, называемых ущербом от недоотпуска электроэнергии. Оптимальный уровень надежности должен

определяться по минимуму общих затрат (см. рисунок 1.49).

Минимум затрат и определяет оптимальный уровень надежности. При этом приращение затрат на повышение надежности равно той экономии, которая получена за счет снижения ущерба.

При оценке надежности используется статистический материал, позволяющий определить вероятности нерабочего q и рабочего p состояния генерирующих блоков, для которых характерно условие q + p = 1. Вероятность нерабочего состояния определяется статистическими показателями потоков отказов и плановых ремонтов, которые зависят от типа оборудования.

Рассмотри простой пример по оценке целесообразности повышения  надежности питания нагрузки по одноцепной ЛЭП путем сооружения второй цепи. Оценим ущерб для существующей схемы при n = 1, который равен: 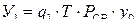       ,                                    (1.68)

где у₀ – удельный ущерб руб/кВт×ч,

P_CP – средняя нагрузка,

T – расчетный срок.

При питании по двум цепям при q ₂ = q₁ ущерб равен .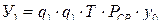

Очевидно, сооружение дополнительной цепи выгодно, если разность ущербов больше приведенных затрат З на сооружение второй цепи, т. е.

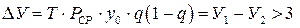.                     (1.69)

Выбор оптимального резерва

Аварийный резерв определяется как разность между располагаемой мощностью и спросом

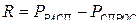,                                        (1.70)

где 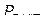 – учитывает фактическую рабочую мощность, а  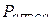– мощность потребителей.

Оба показателя меняются случайно, причем 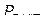 – дискретно, пропорционально мощности блоков, а  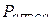– непрерывно. При выборе резерва спрос изменяется дискретно на величину ступени 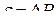, определяемой мощностью минимального блока.

Рассмотрим два дискретных ряда. Первый – ряд вероятностей аварийного выхода разной мощности:

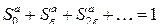,                                         (1.71)

где нижний индекс определяет величину аварийного выхода числом ступеней.

Второй – ряд вероятностей снижения нагрузки относительно максимальной, приведенный к дискретному виду, представим в виде

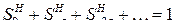.                                     (1.72)

Перемножим оба ряда

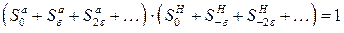           (1.73)

и рассмотрим одно из слагаемых произведения, например, 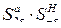, которое определяет вероятность совместного аварийного выхода 2 e при снижении нагрузки на e. Если в часы максимума нагрузки нет резерва, то сумма нижних индексов определяет дефицит мощности, поэтому можно определить вероятность любого дефицита в k e при R =0

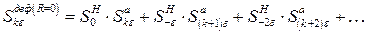                (1.74)

Если в часы максимума нагрузки есть резерв R = r e, то

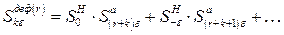                          (1.75)

Ущерб у потребителя за счет недоотпуска электроэнергии за время T:

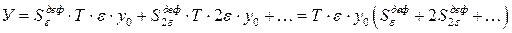(1.76)

Если ввести понятие интегральной вероятности дефицита, определяемой как вероятность некоторого по величине и большего, т.е.

,

,

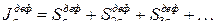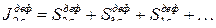то выражение для ущерба (1.76) при любом резерве R = r e  примет вид

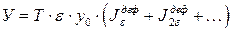.                          (1.77)

Определим целесообразность повышения резерва на величину e МВт до значения 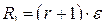, требующего дополнительных затрат .

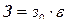При этом ущерб снижается на величину, равную

.

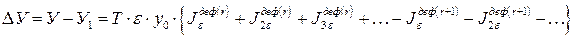Так как 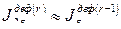, , 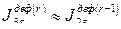…, то они компенсируют друг друга и .

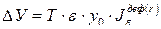Увеличение резерва будет выгодно, когда 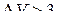, т.е.

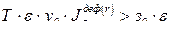, или .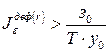

1.24.2. Алгоритм выбора резерва

Блок-схема алгоритма выбора оптимального   резерва приведена на рисунке 1.50. Назначение блоков:

1. Ввод исходной информации;

2. R _ДОП = 0;

3. У⁽⁰⁾ = 0;

4. Определяется ряд снижения нагрузок;

5. Определение членов ряда ….;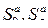

6. 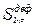,   k = 1,2…;

7. ;

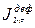8. ;

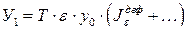9. ;

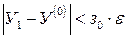10. Печать R _ДОП ;

11. ;

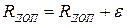12.

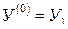
 Рисунок 1.50