Пусть задана только целевая функция без ограничений 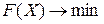, где .

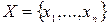Если F (Х) задана аналитически, то, как известно, условие экстремума

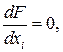                где  i= 1,…,n.                (1.6)

При этом условие минимума определяется знаком .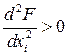

В дальнейшем будут рассматриваться численные методы решения, которые удобны для реализации на ЭВМ. На сегодняшний день большинство таких методов относятся к методам возможных направлений (см. рисунок 1.4).

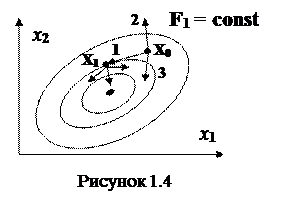Расчет начинается с исходного приближения x ₀. В точке x ₀ наметим несколько направлений 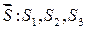. Направления, ведущие к снижению F (здесь 1 и 3) называют возможными направлениями (ВН).

По любому из этих направлений осуществляется переход в следующую точку: 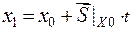,     где t – шаг.

Общее уравнение метода:

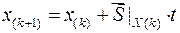,                                            (1.7)

где k – номер итерации (шага).

Величина шага t определяет сходимость процесса: при малом шаге t ® 0 сходимость медленная, но надежная; при  большом t  итерационный процесс может расходиться.

Наилучшая сходимость обеспечивается выбором t _ОПТ по критерию F (Х) ® min на выбранном направлении 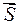. Оптимальный шаг можно выбрать, если учесть, что F (Х) на этом направлении зависит только от величины шага  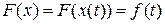и, если удается найти  аналитическую зависимость, то по условию минимума  f ( t ) определяется и 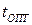. Однако чаще  f ( t ) аппроксимируют кривой второго порядка

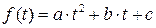.                      (1.8)

Для определения коэффициентов a , b и c необходимо знать f в трех точках:  при t = 0,  когда 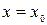 и 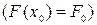;  при t = 1, когда  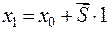и 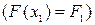 и  при t = 2, когда  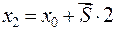и .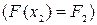

После этого составляют систему уравнений,

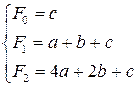                                                (1.9)

решением которой находят a и b , равные

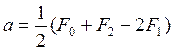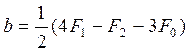 , .                        (1.10)

Из условия минимума функции (1.8)

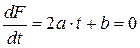
определяется оптимальный шаг

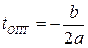
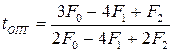              .     (1.11)

Методы, в которых определяется t _ОПТ, называют методами скорейшего поиска. Эти методы широко используются при решении оптимизационных задач. В зависимости от выбора возможных направлений различают несколько методов.

Метод покоординатного спуска

Здесь возможные направления определяются по ортам e_i (единичным векторам) осей координат. Каждая переменная x_i оптимизируется последовательно (см. рисунок 1.5), начиная с x ₁ при фиксированных значениях остальных составляющих

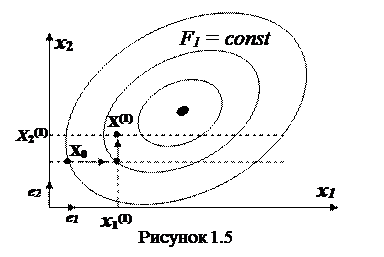
Поиск минимума может проводиться различными методами одномерной оптимизация.

После нахождения 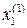 оптимизацию проводят по второй переменной и т.д. до последней, завершающей 1-й цикл. Аналогично проводятся последующие циклы и весь процесс.

Достоинства метода: простота алгоритма. Недостатки: плохая сходимость для функций типа “овраг”.

Градиентный метод

В этом методе возможное направление выбирают противоположным направлению градиента:

                                          .                     

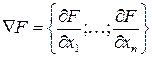Таким образом, основное уравнение градиентного метода:

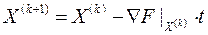                          . (1.12)

Составляющие градиента 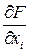 можно найти через конечные приращения (см. рисунок 1.6):

.

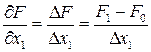Так как 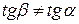, то этот метод имеет погрешность в определении градиента, которая зависит от величины приращения аргумента.

Для снижения погрешности используют метод центриро-ванных приращений 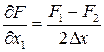, по которому секущая становится почти параллельной касательной, определяющей величину производной.

Градиентный метод часто сочетается с выбором оптимального шага. Для определения величины его используется пробный шаг t ₀, в конце которого определяются координаты Х₁ и составляющие градиента. По значениям градиента в точках Х и Х₁  определяется шаг близкий к оптимальному. Алгоритм метода приведен на рисунке 1.7:

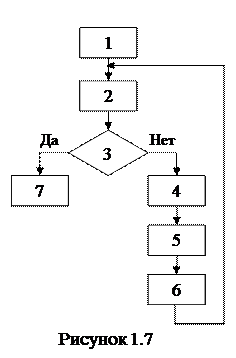
1. Исходное приближение Х = Х ⁽⁰⁾ ;

2. Определение градиента Ñ F |_X;

3. Сравнение | Ñ F| < eps;

4. t₀ и определение ;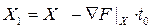

5. Определение градиента в конце пробного шага Ñ F | _{X 1}

6. Определение t _0ПТ и выполнение рабочего шага

             ;

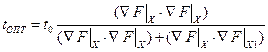
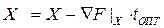7. Выход.

Метод широко используется в  программах оптимизации режимов.

Метод случайного поиска

В данном методе возможные направления определяются с помощью генератора псевдослучайных чисел с равномерным распределением в диапазоне -1,…,1.

Для этого в исходной точке Х⁽⁰⁾ рассматривается n-мерный куб с гранью 2 × d x (см. рисунок 1.8) и считается значение функции F ₀. Случайным образом выбирается точка в кубе 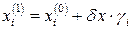, где g_i – псевдослучайное число 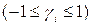. В точке Х⁽¹⁾ считается значение функции F ₁.

Если 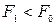, то исходная точка Х^(0)­­­ переносится в точку Х⁽¹⁾ и процедура повторяется. Если 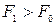, то выбранная точка Х⁽¹⁾ считается неудачной, и вместо нее отыскивается новая точка. Вдали от минимума вероятность попадания в область возможных направлений близка к 50%. По мере приближения к решению величина d x уменьшается.

Достоинства метода: простота алгоритма, не требующего вычисления производных. Недостаток - большое число итераций.