Рассмотрим систему, в которой ГЭС работает на нагрузку параллельно с обобщенной ТЭС.

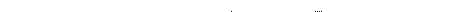
Нагрузка ГЭС однозначно определяется расходом воды из водохранилища, что приводит к изменению уровня ГВБ. Поэтому в качестве оптимизируемой переменной принимаем отметку ГВБ – x ( t ).

Полагаем, что известен цикл t = 24 часа, заданы  отметки ГВБ в начале и в конце цикла регулирования x ₀ и x _К. Известны также прогнозируемый суточный график нагрузки P_H ( t ) (см. рисунок 1.39),  зависимость объема воды в водохранилище от уровня V ( x ) (см. рисунок 1.40):

Задаются также зависимость отметки ГНБ от расхода воды Q (см. рисунок 1.41) и расходная характеристика ТЭС (рисунок 1.42):

Нагрузка ГЭС определяется прогнозом приточности, называемым гидрографом Q _ПР ( t ) (см. рисунок 1.43).

Как известно, метод динамического программирования предназначен для оптимизации многоэтапных процессов. Поэтому суточный цикл разбивается на шаги по времени. Основное уравнение динамического программирования при развитии условной оптимизации с начального состояния

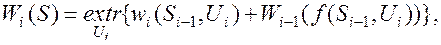               (1.53)

где S– состояние в конце i-го шага,

U_i – управление на i-м шаге,

W_i(S) – условно оптимальная эффективность на всех шагах до  i-го, при условии, что система находится в состоянии S.

U_i(S) – условно оптимальное управление на i-м шаге, совместно с U₁,..,U _{i -1} формирующее вектор оптимального управления.

 Cвойства системы определяют характер зависимости эффекта на шаге w_i(S,U_i) и состояния в начале шага S’=f(S,U_i) как функции только S и управления U_i.

В конце 1-го шага намечается несколько возможных состояний отметки ГВБ, и для каждого определяется расход топлива на ТЭС расчетом по следующему алгоритму:

1) При x ₀ и x_i находим объемы водохранилища V ( x ₀ ), V ( x_i ) и ∆ V ;

2) Считается средний расход воды ;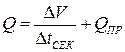

3) По расходу находим отметку x _ГНБ;

4) Определяем средний напор: ;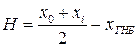

5) Находим мощность ;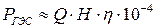

6) Определяем нагрузку ТЭС 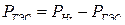 и расход топлива.

На втором шаге в конце его аналогично намечаются возможные состояния, и для каждого состояния рассматривается все переходы из возможных состояний в конце первого. Для каждого перехода по отметкам в начале и в конце по рассмотренному алгоритму считаются расходы топлива на шаге. Условно оптимальное  управление на шаге для рассматриваемого состояния выбирается по минимуму общего расхода на 1-ом и 2-ом шагах, определяющего условно оптимальную эффективность для этого состояния. Это условно-оптимальное управление запоминается. Такая условная оптимизация проводится последовательно для всех этапов, включая и последний.

Оптимальный график находится обратным ходом от x _К к x₀, используя запомненные условно оптимальные управления.

Недостаток метода – большой объем вычислений, который зависит от принятой точности.