Для сложения двух многоразрядных чисел на каждый разряд необходим один полный сумматор.
49 Сумматоры: определение, УГО, сумматор последовательного действия – принцип работы, обобщенная структурная схема, достоинства и недостатки. 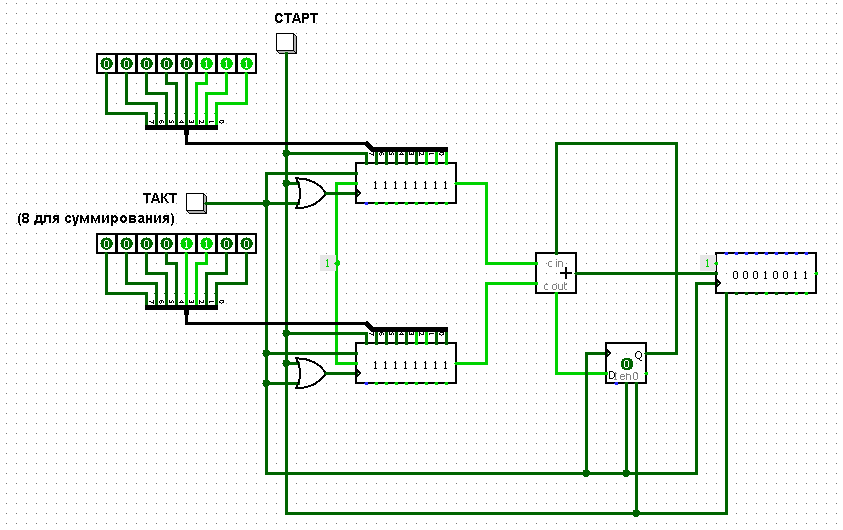

Сумматор последовательного действия состоит из состоит из одноразрядного сумматора, выход переноса которого соединен с его же входом переноса через элемент задержки (D-триггер). Опереция суммирования во всех разрядах слагаемых осуществляется с помощью одного и того же одноразрядного сумматора, но последовательно во времени, начиная с младших разрядов. Сумма накапливается постепенно. Обычно подобный сумматор используется в комбинации со сдвиговыми регистрами.
Достоинство – минимум оборудования.
Недостаток – большое время работы.
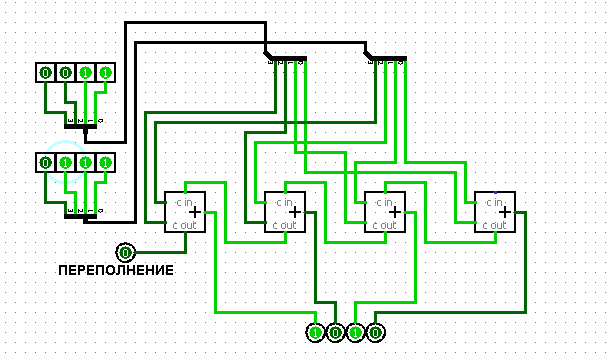
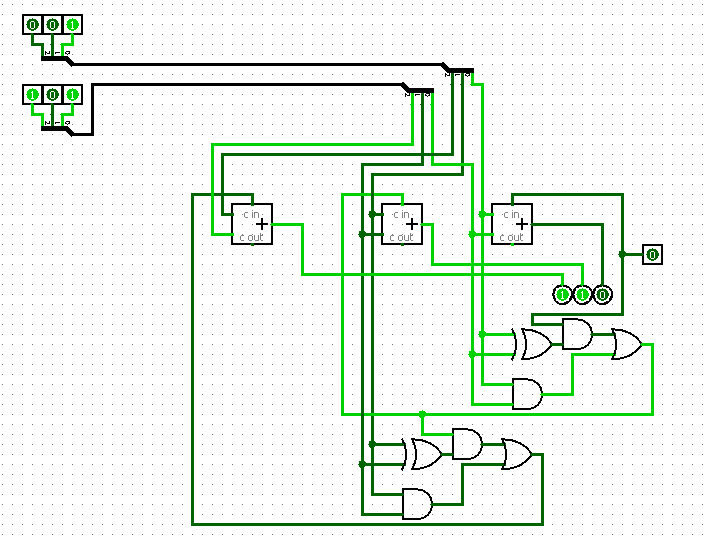
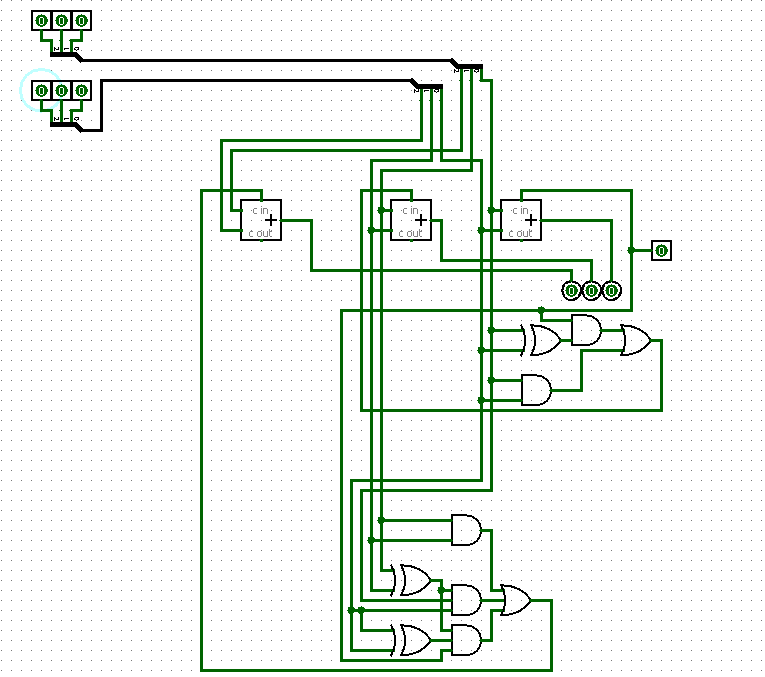
50 Сумматоры: определение, УГО, сумматоры с параллельным переносом – рекуррентная формула для вычисления переносов, пример схемы для 2х разрядного сумматора, достоинства и недостатки.
см. 49,50.
Чтобы уменьшить время операции сложения многоразрядных чисел, можно использовать схемы параллельного переноса. При этом все сигналы переноса вычисляются непосредственно по значениям входных переменных.
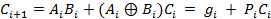
где
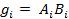
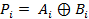
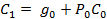
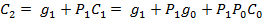
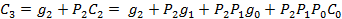
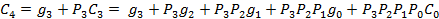
51 Компараторы: определение, таблица истинности, выражения для вычисления отношений «равно» и «больше» на примере компаратора двухразрядных чисел.
Компараторы выполняют операцию определения отношения между числами. Основными отношениями можно считать «равно» и «больше». Все прочие отношения при желании можно выразить как комбинацию основных. Например, «меньше» это отрицание «больше» и отрицание «равно».
| A | B | F1(A>B) | F2(A=B) | F3(A<B) |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
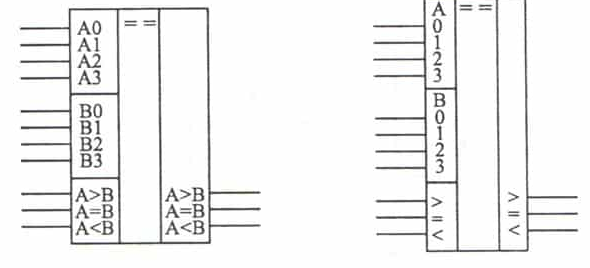
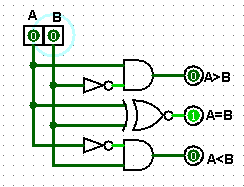
Таблица истинности одноразрядного компаратора с учетом входящих результатов сравнения старших разрядов старших разрядов.
| Ai+1=Bi+1 | Ai+1>Bi+1 | Ai+1<Bi+1 | Ai | Bi | A>B | A=B | A<B |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | * | * | 1 | 0 | 0 |
| 0 | 0 | 1 | * | * | 0 | 0 | 1 |
Признак равенства для одноразрядных чисел:
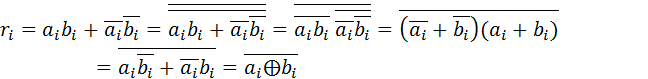
Признак равенства для многоразрядных чисел:
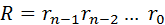
Признак «больше» для двухразрядных чисел:
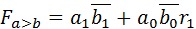
Признак больше для многоразрядных чисел:
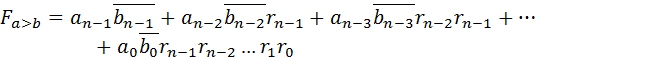
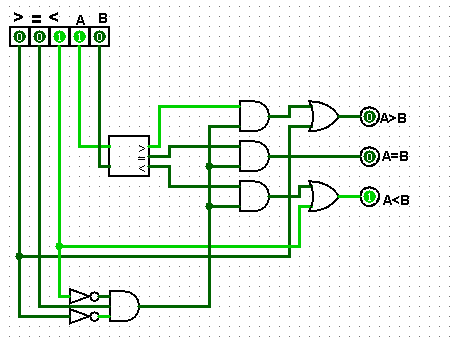
Одноразрядный компаратор с входящими переносами от старшего разряда
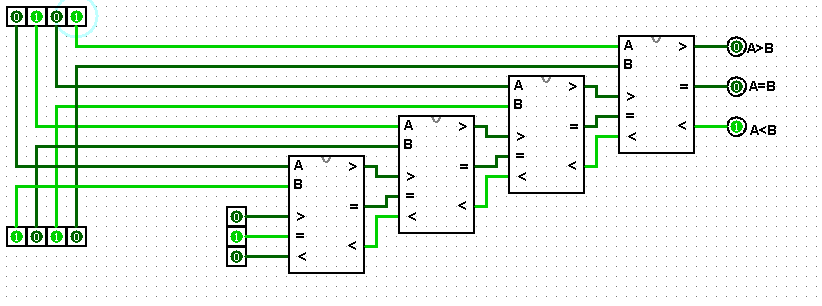
Последовательное наращивание одноразрядных компараторов.
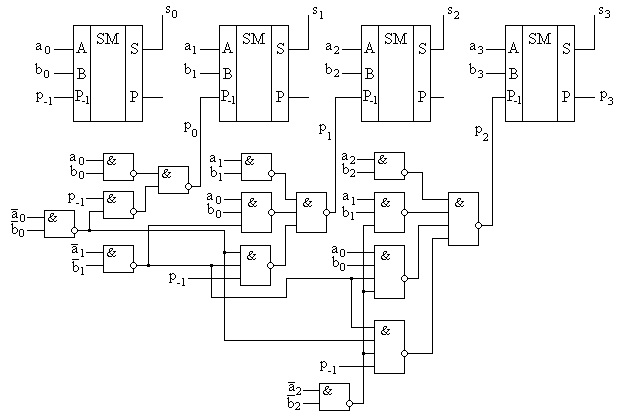
Параллельный четырехразрядный компаратор. 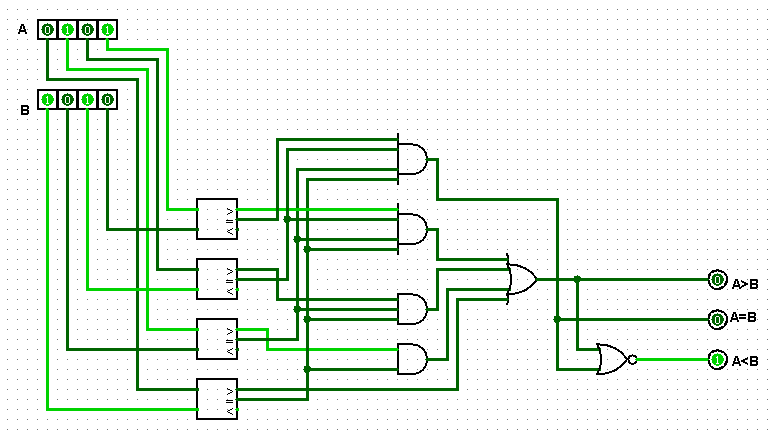
Дата: 2019-04-23, просмотров: 995.