Комбинационные схемы – состояние на выходе в данный момент времени однозначно определяется состояниями на входах в тот же момент времени.

элементы «И», «ИЛИ», «НЕ», «И-НЕ», «ИЛИ-НЕ» (исключение - «ИЛИ»)

· мультипликаторы и демультипликаторы

· шифраторы и дешифраторы

· компараторы

· комбинационные сумматоры

· составные из вышеназванных

Простые цифровые автоматы – состояние на выходе определяется не только состояниями на входах в данный момент времени, но и предыдущим состоянием системы.

· триггеры

· регистры

· счетчики

· составные из вышеназванных

25  Основы алгебры логики: логическая переменная и логическая функция, способы задания логической функции.

Логическая переменная – булева переменная (TRUE/FALSE, 1/0)

Логическая функция – функция от логических переменных/функций. Тоже может быть T/F.

Благодаря тому, что каждая логическая переменная имеет только два значения, множество различных комбинаций входных значений переменных дискретно, конечно и перечеслимо.

Для k логических переменных существует 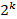 комбинаций и 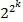уникальных логических функций.

Способы задания:

· Словесный:

описывается фразой на естественном языке.

· Табличный: таблица истинности.

· Аналитический: формулой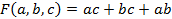

· Векторный: функция задается только перечислением значений на различных наборах. Сами наборы и их кол-во однозначно востанавливаются по кол-ву значений функции.

· Графический: временная диаграмма, осцилограмма, фиклограмма.

· Схемотехнический: комбинационная схема, к-я реализует функцию.

Логические функции от двух переменных: названия, таблицы истинности, УГО.

ФУНКЦИЯ	X1	0	0	1	1
	X2	0	1	0	1
константа – 0	F0	0	0	0	0
конъюнкция	F1	0	0	0	1
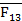
	F2	0	0	1	0
повторение X1	F3	0	0	1	1
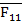
	F4	0	1	0	0
повторение X2	F5	0	1	0	1
сложение по модулю 2 (исключающее «ИЛИ») (либо …, либо…)	F6	0	1	1	0
дизъюнкция	F7	0	1	1	1
элемент Вебба (стрелка Пирса) «ИЛИ-НЕ»	F8	1	0	0	0
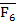
	F9	1	0	0	1
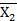
	F10	1	0	1	0
обратная импликация ( 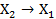)	F11	1	0	1	1
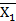
	F12	1	1	0	0
импликация (следование) ( 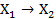)	F13	1	1	0	1
функция Шеффера (штрих Шеффера) «И-НЕ»	F14	1	1	1	0
константа – 1	F15	1	1	1	1

Основные понятия алгебры логики: конъюнкт, дизъюнкт, совершенный конъюнкт, совершенный дизъюнкт, минтерм, макстерм, дизъюнктивная форма, конъюнктивная форма.

Конъюнкт – конъюнкция некоторого кол-ва переменных или их отрицаний.

Дизъюнкт – дизъюнкция некоторого кол-ва переменных или их отрицаний.

Если конъюнкт или дизъюнкт состоит из всех переменных функции, где каждая переменная участвуюет единожды, то он совершенный.

Минтерм (совершенный конъюнкт, конституента единицы) – конъюнкция всех переменных, которые входят в прямом виде, если значение данной переменной в точке определения равно 1, либо в инверсном виде, если значение переменной равно 0. Принимает значение 1 лишь на одном наборе значений переменных (например: 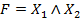). В форму записи минтерма аргумены равные нулю входят с отрицанием. Всего для функции от  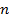переменных можно сформировать  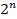минтермов.

Макстерм (совершенный дизъюнкт, конституента нуля) – это дизъюнкция всех переменных, которые входят в прямом виде, если значение данной переменной в точке области определения равно 0, либо в инверсном виде, если значение переменной равно 1. Принимает значение 0 лишь на одном наборе своих аргументов.

ДНФ – дизъюнкция конечного числа конъюнктов.

КНФ – конъюнкция конечного числа дизъюнктов.