Прямой код предназначен для отображения целых и дробных чисел со знаком.
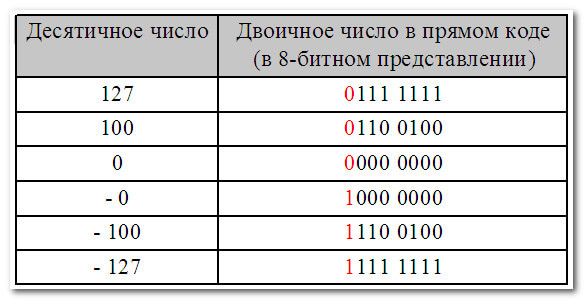
Обратный код. Положительные такие же, как в прямом коде, а отрицательные инвертируются.
Обратный код позволяет вычесть одно число из другого, используя операцию сложения. 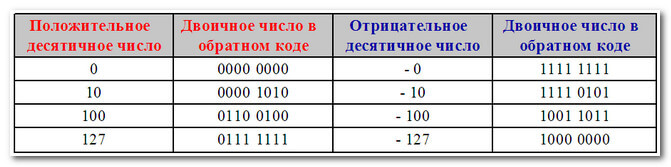
| 1 | 4 | 10 | + | 8 | 10 | = | 2 | 2 | 10 | ||||||||||||||||
| 1 | 4 | 10 | = | 0 | . | 1 | 1 | 1 | 0 | пр | = | 0 | . | 1 | 1 | 1 | 0 | об | |||||||
| 8 | 10 | = | 0 | . | 1 | 0 | 0 | 0 | пр | = | 0 | . | 1 | 0 | 0 | 0 | об | ||||||||
| + | 0 | . | 1 | 1 | 1 | 0 | |||||||||||||||||||
| 0 | . | 1 | 0 | 0 | 0 | ||||||||||||||||||||
| 1 | . | 0 | 1 | 1 | 0 | - переполнение (1. – отрицательное) | |||||||||||||||||||
| + | 0 | . | 0 | 1 | 1 | 1 | 0 | ||||||||||||||||||
| 0 | . | 0 | 1 | 0 | 0 | 0 | |||||||||||||||||||
| 0 | . | 1 | 0 | 1 | 1 | 0 | = | 2 | 2 | 10 | |||||||||||||||
| 1 | 4 | 10 | - | 8 | 10 | = | 2 | 2 | 10 | ||||||||||||||||
| 1 | 4 | 10 | = | 0 | . | 1 | 1 | 1 | 0 | пр | = | 0 | . | 1 | 1 | 1 | 0 | об | |||||||
| - | 8 | 10 | = | 1 | . | 1 | 0 | 0 | 0 | пр | = | 1 | . | 0 | 1 | 1 | 1 | об | |||||||
| + | 0 | . | 1 | 1 | 1 | 0 | |||||||||||||||||||
| 1 | . | 0 | 1 | 1 | 1 | ||||||||||||||||||||
| + | 1 | 0 | . | 0 | 1 | 0 | 1 | ||||||||||||||||||
| 1 | |||||||||||||||||||||||||
| 0 | . | 0 | 1 | 1 | 0 | = | 6 | 10 | |||||||||||||||||
| - | 1 | 4 | 10 | = | 1 | . | 1 | 1 | 1 | 0 | пр | = | 1 | . | 0 | 0 | 0 | 1 | об | ||||||
| - | 8 | 10 | = | 1 | . | 1 | 0 | 0 | 0 | пр | = | 1 | . | 0 | 1 | 1 | 1 | об | |||||||
| + | 1 | . | 0 | 0 | 0 | 1 | |||||||||||||||||||
| 1 | . | 0 | 1 | 1 | 1 | ||||||||||||||||||||
| + | 1 | 0 | . | 1 | 0 | 0 | 0 | ||||||||||||||||||
| 1 | |||||||||||||||||||||||||
| 0 | . | 1 | 0 | 0 | 1 | - переполнение | |||||||||||||||||||
| + | 1 | . | 1 | 0 | 0 | 0 | 1 | ||||||||||||||||||
| 1 | . | 1 | 0 | 1 | 1 | 1 | |||||||||||||||||||
| + | 1 | 1 | . | 0 | 1 | 0 | 0 | 0 | |||||||||||||||||
| 1 | |||||||||||||||||||||||||
| 1 | . | 0 | 1 | 0 | 0 | 1 | = | 1 | . | 1 | 0 | 1 | 1 | 0 | пр | = | - | 2 | 2 | 10 | |||||
Дополнительный код.
Положительные такие же как и в прямом и обратном кодах.
Отрицательные:
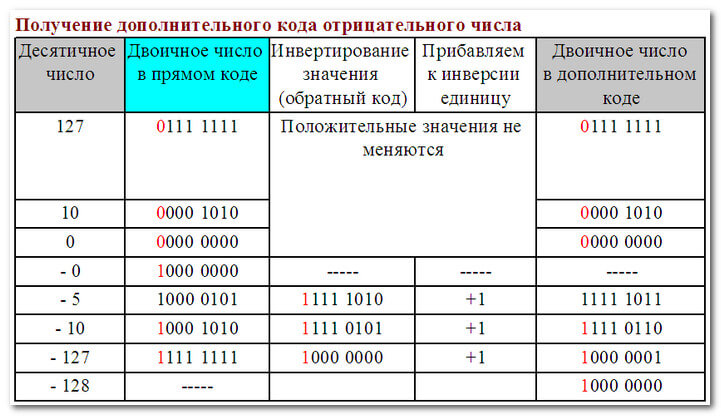
1 способ: к младшему разряду обратного кода прибавляется единица.
| - | 1 | 4 | 10 | = | 1 | . | 1 | 1 | 1 | 0 | пр | = | 1 | . | 0 | 0 | 0 | 1 | об | = | 1 | . | 0 | 0 | 1 | 0 | дп |
| - | 8 | 10 | = | 1 | . | 1 | 0 | 0 | 0 | пр | = | 1 | . | 0 | 1 | 1 | 1 | об | = | 1 | . | 1 | 0 | 0 | 0 | дп |
2 способ: переписываем прямой код справа налево до первой единицы включительно, остальные инвертируем.
| - | 1 | 4 | 10 | = | 1 | . | 1 | 1 | 1 | 0 | пр | = | 1 | . | 0 | 0 | 1 | 0 | дп |
| - | 8 | 10 | = | 1 | . | 1 | 0 | 0 | 0 | пр | = | 1 | . | 1 | 0 | 0 | 0 | дп |
3 способ: вычитаем из нуля двоичный код числа.
Сложение:
Вычеркиваем все символы справа от первого после точки.
| 6 | 10 | = | 0 | . | 1 | 1 | 0 | пр | = | 0 | . | 1 | 1 | 0 | дп | |||||||||||||||
| - | 6 | 10 | = | 1 | . | 1 | 1 | 0 | пр | = | 1 | . | 0 | 1 | 0 | дп | ||||||||||||||
| + | 0 | . | 1 | 1 | 0 | |||||||||||||||||||||||||
| 1 | . | 0 | 1 | 0 | ||||||||||||||||||||||||||
| 1 | 0 | . | 0 | 0 | 0 | = | 0 | 10 | ||||||||||||||||||||||
| - | 8 | 10 | = | 1 | . | 1 | 0 | 0 | 0 | пр | = | 1 | . | 1 | 0 | 0 | 0 | дп | ||||||||||||
| - | 1 | 4 | 10 | = | 1 | . | 1 | 1 | 1 | 0 | пр | = | 1 | . | 0 | 0 | 1 | 0 | дп | |||||||||||
| + | 1 | . | 1 | 0 | 0 | 0 | ||||||||||||||||||||||||
| 1 | . | 0 | 0 | 1 | 0 | |||||||||||||||||||||||||
| 1 | 0 | . | 1 | 0 | 1 | 0 | - переполнение (получили положительное знач.) | |||||||||||||||||||||||
| + | 1 | . | 1 | 1 | 0 | 0 | 0 | |||||||||||||||||||||||
| 1 | . | 1 | 0 | 0 | 1 | 0 | ||||||||||||||||||||||||
| 1 | 1 | . | 0 | 1 | 0 | 1 | 0 | = | 1 | . | 0 | 1 | 0 | 0 | 1 | = | 1 | . | 1 | 0 | 1 | 1 | 0 | пр | = | 2 | 2 | 10 | ||
Модифицированный код.
1.1011 – отрицательное число или положительное с переполнением?
Модификация – два разряда для знака.
00. – положительное.
11. – отрицательное.
01. – положительное с переполнением.
10. – отрицательное с переполнением.
В дополнительном коде сложение отрицательных и положительных чисел происходит по одному правилу. + меньше памяти занимает.
Понятие разрядной сетки. Понятие переполнения. Понятие машинного нуля.
Разрядная сетка – это кол-во двоичных разрядов, выделяемых в памяти для отображения чисел. Она напрямую зависит от разрядности процессора. Если число вышло за пределы разрядной сетки слева, то говорят о переполнении разрядной сетки. Если справа – то о возникновении машинного нуля.
Сложение и вычитание в обратном и дополнительном коде. Переполнение и его устранение.
см. 13.
Дата: 2019-04-23, просмотров: 552.