Свойства информации: объективность, точность, достоверность, полнота, актуальность, полезность, синтаксическая адекватность, связность, осмысленность, неисчерпаемость.
· объективность:
не зависит от методов ее фиксации, чьего-либо мнения.
· точность:
определяется степенью ее близости к реальному состоянию.
· достоверность:
общая точность и полнота информации. Объективная информация всегда достоверна, субъективная – не всегда.
· полнота:
информация может считаться полной, если достаточна для решения задачи.
· актуальность:
степень важности информации непосредственно в данных условиях/времени.
· полезность:
степень применимости пользователем.
· синтаксическая адекватность:
Характеризуется возможностью успешно получить информацию(интерпретировать данные):
o тип носителя
o скорость передачи
o способы кодировки
o точность предстваления
· связность:
привязанность к носителю.
· осмысленность:
смысл сохраняется независимо от формы предстваления информации.
· неисчерпаемость:
физически не стареет, тиражируется, копится, передается от поколения к поколению.
3 Информатика как междисциплинарное научное направление: основные взгляды на содержание информатики.
Информатика – междисциплинарное научное направление, изучающее вопросы производства, хранения, накопления, передачи, обработки и использования информации.
1 концепция – информатика без вычислительной техники существовать не может.
2 концепция – информатика, как методология работы с информацие, существовала в том или ином виде всегда. Информатика – информационная культура личности человека.
Информационное общество. Признаки перехода к информационному обществу.
1. Объектом и результатом труда большей части населения является информация.
2. Информация – това, определяющий основные экономические показатели.
3. Нет проблем с доступом к информации.
4. Существует необходимая техническая база для распространения и обработки информации.
5. Информация – оружие.
5 Системы счисления: определение, классификация, позиционные системы счисления и их основные понятия, сокращенная и полиномиальная запись чисел.
Система счисления(СС) — правила наименования и записи чисел, а также выполнения арифметических операций. В каждой СС есть свой набор базовых символов.
| СС |
| позиционные |
| не позиционные |
| традиционные k-ичные 2-ичная 10-ичная … |
| смешанные k-q-ичные 2-10-чная … |
| аддитивные факторианая фибоначчева … |
| прочие |
В позиционных СС значение цифры зависит от позиции (разряда).
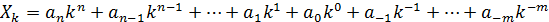
Перевод целых чисел из 10ой системы счисления в систему с основанием N по машинному алгоритму и методом подбора.
Машинный алгоритм.
12510
| 125 | 2 | |||||
| 124 | 62 | 2 | ||||
| 1 | 62 | 31 | 2 | |||
| 0 | 30 | 15 | 2 | |||
| 1 | 14 | 7 | 2 | |||
| 1 | 6 | 3 | 2 | |||
| 1 | 2 | 1 | ||||
| 1 |
12510=11111012
Метод подбора.
34210=256+(342-256)=28+86=28+64+(86-64)=28+26+22=28+26+16+4+2=28+26+24+22+21
34210=1*28+0*27+26+0*25+24+0*23+22+21+0*20
34210=101010110
Перевод вещественных чисел из 10ой системы счисления в систему с основанием N по машинному алгоритму.
0.62510
| * | 0.625 |
| 2 | |
| 1.250 |
|
|
| |||||||||||||||
| 1 | 0 | 1 | |||||||||||||||
|
| |||||||||||||||||
0.62510=0.1012
Понятие разрядной сетки. Понятие переполнения. Понятие машинного нуля.
Разрядная сетка – это кол-во двоичных разрядов, выделяемых в памяти для отображения чисел. Она напрямую зависит от разрядности процессора. Если число вышло за пределы разрядной сетки слева, то говорят о переполнении разрядной сетки. Если справа – то о возникновении машинного нуля.
Сложение и вычитание в обратном и дополнительном коде. Переполнение и его устранение.
см. 13.
Правила выполнения арифметических операций для чисел с плавающей точкой. Примеры.
Сложение/вычитание:
1. Выравниваем порядки.
2. Складываем/вычитаем.
3. Нормализуем.
Умножение:
1. Складываем порядки.
2. Перемножаем мантиссы.
3. Нормализуем.
Деление:
1. Вычитаем порядок делителя из порядка делимого.
2. Делим.
3. Нормализуем.
| 0 | . | 1 | * | 2 | ^ | 5 | и | 0 | . | 1 | * | 2 | ^ | 3 | ||||||||||||||||
| + | 0 | . | 1 | 0 | 0 | * | 2 | ^ | 5 | + | 0 | . | 1 | 0 | 0 | * | 2 | ^ | 5 | |||||||||||
| 0 | . | 0 | 0 | 1 | * | 2 | ^ | 5 | 0 | . | 0 | 0 | 1 | * | 2 | ^ | 5 | |||||||||||||
| 0 | . | 1 | 0 | 1 | * | 2 | ^ | 5 | 0 | . | 0 | 1 | 1 | * | 2 | ^ | 5 | = | 0 | . | 1 | 1 | * | 2 | ^ | 4 | ||||
| * | 0 | . | 1 | * | 2 | ^ | 5 | |||||||||||||||||||||||
| 0 | . | 1 | * | 2 | ^ | 3 | ||||||||||||||||||||||||
| 0 | . | 0 | 1 | * | 2 | ^ | 8 | = | 0 | . | 1 | * | 2 | ^ | 7 | |||||||||||||||
|
| 0 | . | 1 | * | 2 | ^ | 5 | |||||||||||||||||||||||
| 0 | . | 1 | * | 2 | ^ | 3 | ||||||||||||||||||||||||
| 1 | * | 2 | ^ | 2 | = | 0 | . | 1 | * | 2 | ^ | 3 |
Основные понятия алгебры логики: конъюнкт, дизъюнкт, совершенный конъюнкт, совершенный дизъюнкт, минтерм, макстерм, дизъюнктивная форма, конъюнктивная форма.
Конъюнкт – конъюнкция некоторого кол-ва переменных или их отрицаний.
Дизъюнкт – дизъюнкция некоторого кол-ва переменных или их отрицаний.
Если конъюнкт или дизъюнкт состоит из всех переменных функции, где каждая переменная участвуюет единожды, то он совершенный.
Минтерм (совершенный конъюнкт, конституента единицы) – конъюнкция всех переменных, которые входят в прямом виде, если значение данной переменной в точке определения равно 1, либо в инверсном виде, если значение переменной равно 0. Принимает значение 1 лишь на одном наборе значений переменных (например: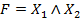 
). В форму записи минтерма аргумены равные нулю входят с отрицанием. Всего для функции от 
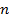переменных можно сформировать 
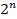минтермов.
Макстерм (совершенный дизъюнкт, конституента нуля) – это дизъюнкция всех переменных, которые входят в прямом виде, если значение данной переменной в точке области определения равно 0, либо в инверсном виде, если значение переменной равно 1. Принимает значение 0 лишь на одном наборе своих аргументов.
ДНФ – дизъюнкция конечного числа конъюнктов.
КНФ – конъюнкция конечного числа дизъюнктов.
Минимизация логических функций методом диаграмм Вейча: идея метода, понятие интервала логической функции, формы интервалов, правила выделения интервалов, правила построения диаграммы с целью получения МДНФ функции от 3-х переменных, алгоритм минимизации.
См. 32.
Минимизация логических функций методом диаграмм Вейча: идея метода, понятие интервала логической функции, формы интервалов, правила выделения интервалов, правила построения диаграммы с целью получения МДНФ функции от 4-х переменных, алгоритм минимизации.
Решение:
F=6EB9;
F2=0110111010111001
Таблица истинности:
| A | B | C | D | F(A,B,C,D) |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Построение МДНФ:
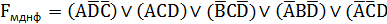
МДНФ в базисе «И-НЕ»:
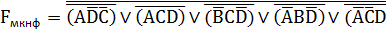
МДНФ в базисе «ИЛИ-НЕ»:
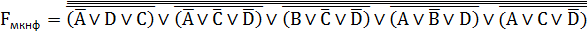
Построение МКНФ:
берем дизъюнкты с отрицанием каждого члена отдельно:
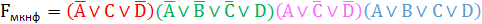
МКНФ в базисе «И-НЕ»:
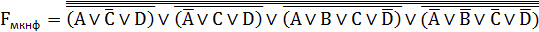
МКНФ в базисе «ИЛИ-НЕ»:
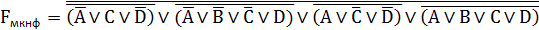
Минимизация логических функций методом диаграмм Вейча: идея метода, понятие интервала логической функции, формы интервалов, правила выделения интервалов, правила построения диаграммы с целью получения МКНФ функции от 3-х переменных, алгоритм минимизации.
См. 32.
Минимизация логических функций методом диаграмм Вейча: идея метода, понятие интервала логической функции, формы интервалов, правила выделения интервалов, правила построения диаграммы с целью получения МКНФ функции от 4-х переменных, алгоритм минимизации.
См. 32.
Таблица истинности.
| A | B | C | D | F(A,B,C,D) |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Реализация функции при помощи мультиплексора 16-1.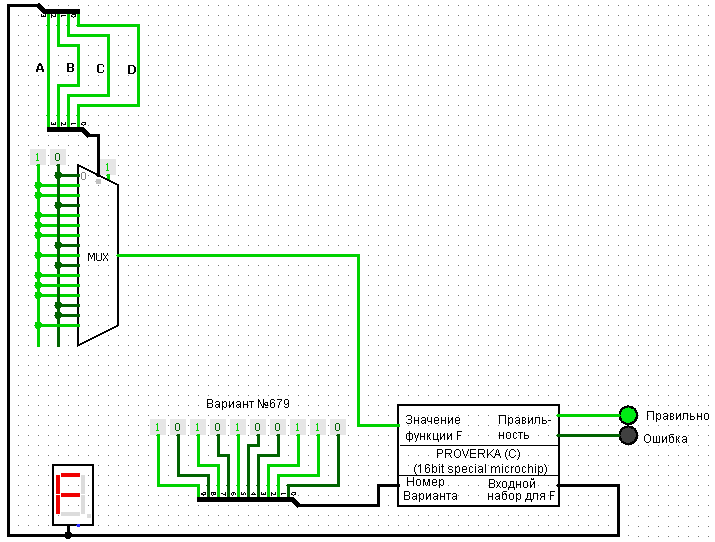 
Реализация функции при помощи мультиплексора 8-1. 
Реализация функции при помощи мультиплексоров 4-1.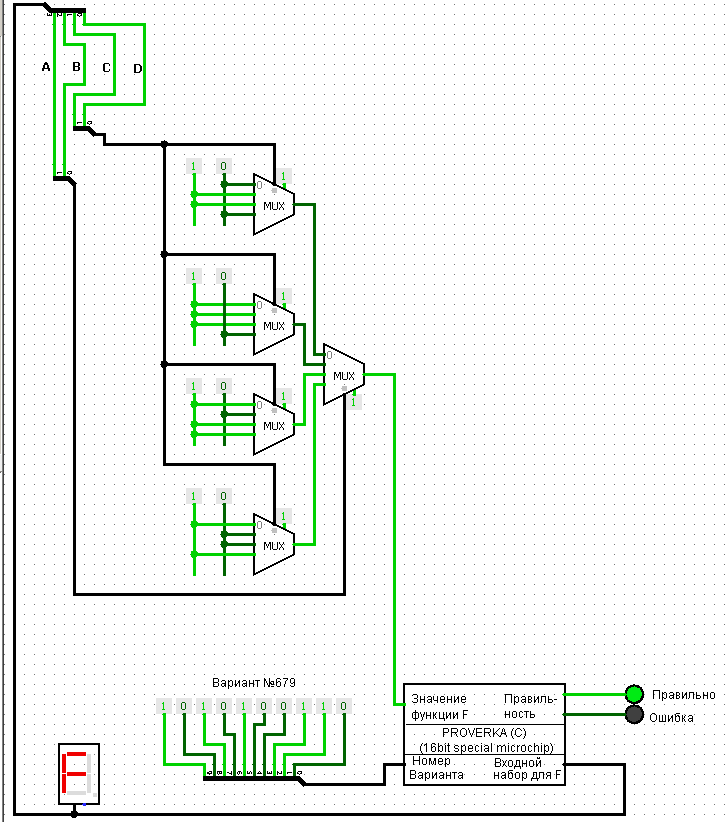 
Реализация функции при помощи мультиплексоров 2-1 и одного мультиплексора 4-1.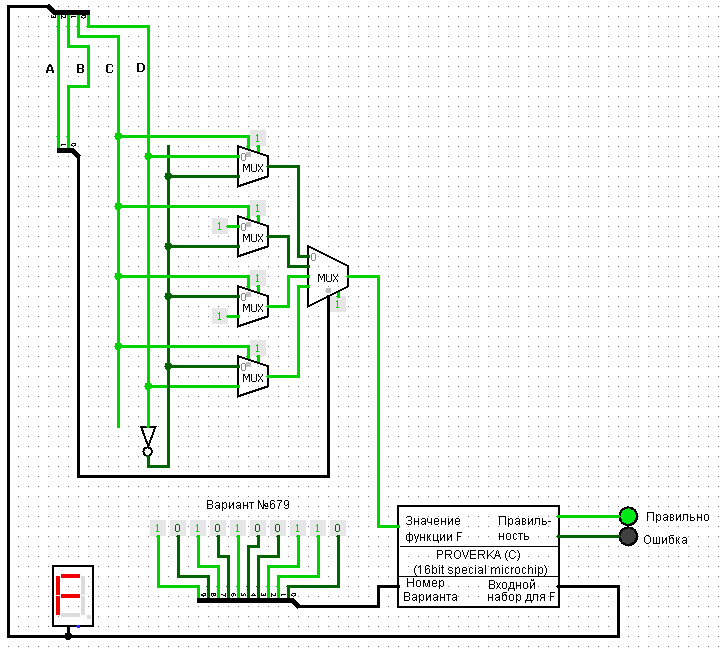 
Метод «сверху-вниз».
При разработке алгоритма или программы, первоначально реализуется основной управляющий алгоритм без детализации функциональных элементов, которые заменяются функциями-заглушками, возвращающими постоянное значение.
По мере разработки каждая функция-заглушка реализуется своим алгоритмом, вызывающим, при необходимости, другие функции-заглушки.
Разработка заканчивается когда все функции-заглушки реализованы в виде набора базовых конструкций.
Метод «снизу-вверх».
Предполагает обратный путь разработки: Сначала реализуются элементарные функции из которых собираются более сложные конструкции. В настоящее время активно используется, так как существует большое количество библиотек, содержащих готовые функции.
Операции с данными.
Все операнды функций, имеющих ограничения на область допустимых значений (ОДЗ), должны в обязательном порядке проверяться на соответствие ОДЗ.
Свойства информации: объективность, точность, достоверность, полнота, актуальность, полезность, синтаксическая адекватность, связность, осмысленность, неисчерпаемость.
· объективность:
не зависит от методов ее фиксации, чьего-либо мнения.
· точность:
определяется степенью ее близости к реальному состоянию.
· достоверность:
общая точность и полнота информации. Объективная информация всегда достоверна, субъективная – не всегда.
· полнота:
информация может считаться полной, если достаточна для решения задачи.
· актуальность:
степень важности информации непосредственно в данных условиях/времени.
· полезность:
степень применимости пользователем.
· синтаксическая адекватность:
Характеризуется возможностью успешно получить информацию(интерпретировать данные):
o тип носителя
o скорость передачи
o способы кодировки
o точность предстваления
· связность:
привязанность к носителю.
· осмысленность:
смысл сохраняется независимо от формы предстваления информации.
· неисчерпаемость:
физически не стареет, тиражируется, копится, передается от поколения к поколению.
3 Информатика как междисциплинарное научное направление: основные взгляды на содержание информатики.
Информатика – междисциплинарное научное направление, изучающее вопросы производства, хранения, накопления, передачи, обработки и использования информации.
1 концепция – информатика без вычислительной техники существовать не может.
2 концепция – информатика, как методология работы с информацие, существовала в том или ином виде всегда. Информатика – информационная культура личности человека.
Дата: 2019-04-23, просмотров: 698.
