Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

В реакторе конечных размеров имеет место утечка нейтронов из объема ре­актора. Характеристикой цепной реакции деления в конечном реакторе служит эффективный коэффициент размножения:

,

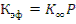где 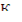 — коэффициент размножения нейтронов в бесконечной среде, опреде­ляемый только свойствами среды; Р — вероятность избежать утечки, слабо за­висящая от энергии нейтронов и значительно - от геометрических характери­стик реактора (формы и размеров) и его состава.

Уравнения диффузии

 

Для вывода уравнения реактора в диффузионно-возрастном приближении реакторные нейтроны условно разделяются на две группы:

1) замедляющиеся нейтроны с энергией от 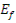- до  Е_гр;

2) тепловые нейтроны с энергией Е<Е_гр.

Предполагаем, что захват нейтронов в процессе замедления отсутствует, а всё резонансное поглощение сосредоточено на границе области замедления (Е_гр) и плотность замедления q ( r , τ_т) скачком уменьшается в φ раз (φ- вероят­ность избежать резонансного захвата).

Тогда для замедляющихся нейтронов справедливо уравнение возраста:

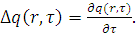                                                                                       (10.1)

Диффузию тепловых нейтронов будем описывать следующим уравнением:

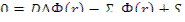                                                                     (10.2)

где Ф(r) - плотность полного потока тепловых нейтронов; D , Σ_a — константы, усредненные по энергии тепловой области; S — объемная скорость генерации тепловых нейтронов (источник). В этом случае S выражается через плотность замедления при τ=τ_т, т.е. S=φ q ( r , τ_т). Под пространственной переменной r по­нимается 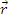, например, .

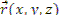Начальные условия для плотности замедления

 

На каждый поглощенный тепловой нейтрон генерируется 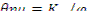  быстрых нейтронов. Полное число поглощений тепловых нейтронов в единице объема в единицу времени - Σ_аФ( r ). Тогда объемная скорость генерации быстрых нейтронов

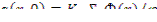
Граничные условия

q ( R _э , τ )=0; Ф(R_э)=0,

где R _э - экстраполированный размер реактора (активной зоны).

Уравнение реактора

Аналитические решения записанных уравнений в частных производных мо­гут быть получены методом разделения переменных, который приводит к не­скольким обыкновенным дифференциальным уравнениям с известными реше­ниями. Этот метод предполагает независимость каждого решения в функции одной переменной от всех остальных переменных. Такое требование выполня­ется только для ограниченного числа случаев физических задач.

В рассматриваемом случае разделение пространственных и энергетических переменных возможно только тогда, когда мощность источников быстрых ней­тронов в каждой точке объема пропорциональна числу замедляющихся нейтро­нов с любой энергией. При этом энергетический спектр замедляющихся ней­тронов, несмотря на диффузию при замедлении, одинаков во всем объеме. Та­кая картина наблюдается в однородной размножающей среде, граничащей только с пустотой, т.е. в гомогенном реакторе без отражателя нейтронов.

В случае гомогенного реактора переменные разделяются, т.е. q ( r , τ )= R ( r ) T ( τ ), где R , Т— некоторые функции. Тогда уравнение возраста (10.1) можно записать:

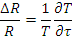
Приравняв обе части константе (— 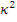 ), получим два уравнения:

                                                

 

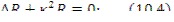
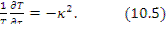
Решение уравнения (10.5):

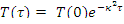 - спектр замедляющихся нейтронов в реакторе конечных раз­меров. Причиной убыли нейтронов при замедлении в отсутствие поглощения являются утечки из конечного объема.

Плотность замедления с учетом начального условия (10.3):

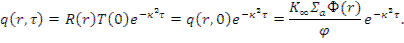
Функция пространственного распределения замедляющихся нейтронов R ( r ) пропорциональна плотности потока тепловых нейтронов Ф( r ):

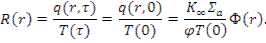
При этом уравнение (10.4) справедливо и для функции Ф( r ). В самом деле, под­ставив последнее выражение в уравнение (10.4), получим

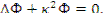
Таким образом, пространственные распределения замедляющихся и тепло­вых нейронов в гомогенном реакторе без отражателя одинаковы. Они опреде­ляются уравнениями (10.4) или (10.6) и размерами тела, в котором протекает цепная реакция. Через размеры тела выражается константа 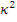 при выборе ре­шений, удовлетворяющих уравнению (10.6) и граничным условиям. Следовательно, константа  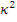в уравнении (10.6) в неявном виде представляет критиче­ские размеры реактора без отражателя.

Уравнение (10.6) называется уравнением реактора или волновым уравне­нием (в математике уравнением Гельмгольца).

Критическое уравнение

Если константу 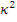 выразить через коэффициенты рассмотренных уравне­ний, то критические размеры окажутся связанными непосредственно с диффу­зионными константами и 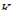, т.е. будет установлена зависимость между свой­ствами размножающей среды и критическими размерами.

Источниковый член, входящий в уравнение диффузии (10.2),

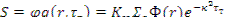
 Подставив его в уравнение диффузии (10.2), получим

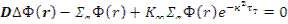
или (с учетом )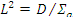

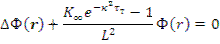
Сопоставив данное уравнение с уравнением (10.6), получим

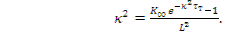                                           (10.7)

После преобразований уравнения (10.7) получается следующее:

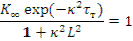
Это уравнение связывает материальные характеристики среды ( 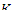, τ, 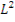) с критическими размерами реактора без отражателя, представленными неявно параметром 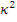, и называется критическим уравнением в диффузионно-возрастном приближении. Параметр  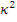как решение уравнения (10.8) называется материальным параметром размножающей среды .

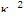В критическом реакторе 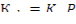 =1, поэтому вероятность избежать утечки

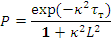
где 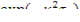 представляет собой вероятность для нейтронов, имеющих возраст τ_т, избежать утечки в процессе замедления, а  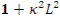  есть вероятность для тепловых нейтронов избежать утечки в процессе диффузии. В самом деле, доля поглощенных тепловых нейтронов в произвольном единичном объеме

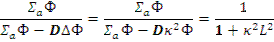
 (с учетом (10.6)), которая равна доле поглощений во всем объеме реактора, так как не зависит от пространственных координат.

В достаточно большом критическом реакторе, где утечка достаточно мала,

т.е. Р и 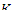 мало отличаются от единицы 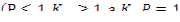), можно прибли­женно преобразовать уравнение (10.7) (либо (10.8)), используя разложение экспоненты в ряд и ограничившись линейным приближением, т.е. принять 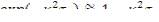. Тогда получим приближенное явное выражение для матери­ального параметра критического уравнения (одногрупповое приближение):

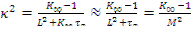                                           (10.9)

Тогда вероятность избежать утечки в таком реакторе

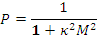
Геометрический параметр для реакторов различной формы

Параметр 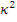 как решение уравнения (10.6), выраженный через геометрические размеры реактора, называется геометрическим параметром —  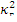. В данном случае критического состояния реактора материальный и геометрический параметры совпадают -  = .

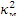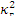В некритическом реакторе материальный параметр не равен геометриче­скому. В общем случае некритического состояния геометрический параметр — это наименьшее собственное число ортогональных собственных функций, со­ставляющих общее решение нестационарного уравнения реактора. Все собст­венные числа зависят от формы и размеров тела.

Рассмотрим ряд простейших форм реактора. Функция распределения плот­ности потока нейтронов, удовлетворяющая эллиптическому уравнению (10.6) и симметричным граничным условиям, будет обладать той же симметрией. Ре­шения данного уравнения могут быть получены в координатах, обладающих симметрией задачи.

1. Плоский реактор бесконечного размера

Пластина обладает симметрией относительно центральной плоскости, на которой выбирается начало координатной оси в перпендикулярном направле­нии (рис.10.1). Лапласиан - 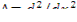, тогда уравнение (10.6) запишется как

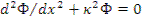
Решение находится при нулевых граничных условиях — Ф(x) должен обращаться в нуль на экстраполированных границах: ,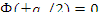

где а_э=а+2 d _э , a-ширина пластины; d _э - длина линейной экстраполяции. Решение находится в виде

Ф(х) = A cos κх + С sin κх,

где А и С- константы интегрирования. Константа С должна быть равна нулю, так как синус - функ­ция несимметричная. Константа 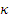 определяется из указанного ранее граничного условия - коси­нус обращается в нуль при равенстве аргумента

числу, кратному π/2, т.е. 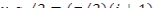, где i=0,1,2,3... Отсюда 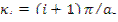. Следовательно, существует бесчисленное множество чисел  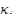и соответствую­щих им функций 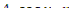, удовлетворяющих условиям задачи. В точно кри­тическом реакторе все коэффициенты 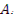, кроме А₀, обращаются в нуль. Квадрат соответствующего числа  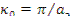есть геометрический параметр, т.е.  .

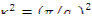 Решением является функция

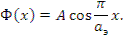
Константа А не определена, поскольку начальное условие по времени не ис­пользовалось. Константа А — плотность потока нейтронов в центральной плос­кости, т.е. A=Ф(0). Плотность потока нейтронов в каждой точке критического реактора может быть любой - такой, какой она была в начальный момент вре­мени, когда реактор достиг критичности.

Функция плотности потока нейтронов Ф(х) симметрична относительно цен­тральной плоскости. Важнейшей характеристикой распределения плотности потока нейтронов является коэффициент неравномерности:

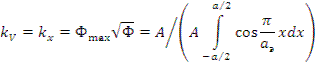
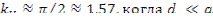
2. Реактор в форме параллелепипеда

Прямоугольный параллелепипед обладает симметрией относительно плос­костей, проходящих через центр параллельно граням. Симметрией параллеле­пипеда обладают декартовы координаты. На рис. 10.2 начало координат в цен­тре параллелепипеда.

Лапласиан -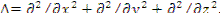

Граничные условия:

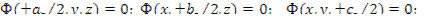
где a _э = a +2 d _э ; b _э = b +2 d _э ; c _э = c +2 d _э ; a , b , c — ширина сторон прямоугольника соответственно по осям х, у, z .

Решение находится методом разделения переменных. Функция плотности потока нейтронов Ф(х,у, z ) представляется в виде Ф(x,y,z)=X(x)Y(y)Z(z).

Подстановка ее в уравнение реактора дает

 

 

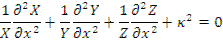
Поскольку функции X , Y и Z зависят каждая от своей независимой переменной и 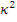   является константой, то каждое из слагаемых данного уравнения должно быть константой. Все координаты равноправны, значит кон­станты должны быть одного знака, а так как  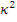больше нуля, константы отрицательны. После обозначения  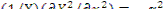и т.д. имеем

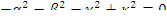
и три уравнения типа

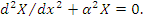
Решение записанного уравнения

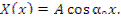
Квадрат числа 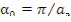 называется составляющей геометрического параметра

по оси х.

Решения по остальным координатам аналогичны и после их подстановки в выражение для Ф(х,у, z ) функция плотности потока нейтронов примет вид:

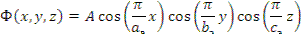
Геометрический параметр

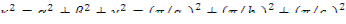
Константа А — плотность потока нейтронов в центре параллелепипеда, т.е. A=Ф(0,0,0).

Коэффициент неравномерности

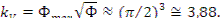
3. Сферический реактор

Шар обладает симметрией относительно центра. Той же симметрией обла­дают сферические координаты с началом координат в центре сферы (рис. 10.3). Сферическая симметрия приводит к независимости плотности потока нейтро­нов от угловых координат, т.е. к зависимости только от радиуса r .

Лапласиан - .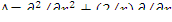

Граничное условие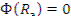

где R _э = R + d _э ; R - радиус шара.

Решение находится с помощью подстановки Ф( r )= u / r — уравнение приводится к виду

d ² u / dr ² + κ ² u = 0.

Решение находится в виде

u(r) = A sin κr + С cos κr,

где А и С— константы интегрирования. После пе­рехода к Ф( r ):

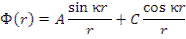
Константа С должна быть равна нулю, так как в центре реактора (в области оп­ределения) функция Ф( r ) обращается в бесконечность. Константа к определяет­ся из указанного ранее граничного условия — синус обращается в нуль при ра­венстве аргумента числу, кратному π, т.е. 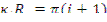, где i=0,1,2,3... Отсюда 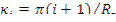. В критическом реакторе все коэффициенты A_i , кроме A ₀ , обраща­ются в нуль. Квадрат соответствующего числа  есть геометрический параметр, т.е. .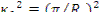

Решением является функция

 

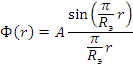
Константа А — плотность потока нейтронов в центре шара, т.е. A=Ф(0). Коэффициент неравномерности

 

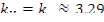
4. Реактор в форме бесконечного кругового цилиндра

Круговой цилиндр обладает осевой симметрией. Той же симметрией обла­дают цилиндрические координаты с началом ко­ординатной оси на центральной оси цилиндра (рис. 10.4). Осевая симметрия приводит к незави­симости плотности потока нейтронов от угловой координаты, а в бесконечном цилиндре плот­ность потока не зависит и от высотной координа­ты, т.е. зависит только от радиуса r .

Лапласиан - .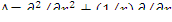

Граничное условие

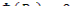
где R _э = R + d _э ; R - радиус цилиндр

Исходное уравнение с помощью замены х= κr приводится к виду

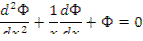
Решение находится в виде

Ф(х)=АJ₀ (х)+СY₀ (х),

 где J₀, Y₀ — функции Бесселя нулевого порядка первого и второго рода соответственно. Константа С должна быть равна нулю в соответствии с требованием конечности решений, так как при r=0 Y₀ (κr )—>oo. Константа κ  определяется из граничного условия. У функции J₀ корней бесчисленное множество, так что существует бесчисленное множество чисел κ_i - и соответствующих им функций Ai J₀(κ_ir), удовлетворяющих условиям задачи. В критическом реакторе все ко­эффициенты A_i , кроме А₀, обращаются в нуль. Первый корень функции Бесселя κ₀R_э=2,405. Квадрат соответствующего числа κ₀=2,405/R_Э есть геометрический параметр, т.е. 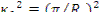. Решением является функция

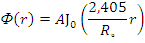
Константа А — плотность потока нейтронов в центре цилиндра, т.е. А=Ф(0). Коэффициент неравномерности

 

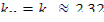
5. Реактор в форме конечного кругового цилиндра

В конечном круговом цилиндре плотность потока нейтронов не зависит от угловой координаты, т.е. зависит только от высотной координаты z и радиуса r. Начало цилиндрических координат выбирается в центре цилиндра (рис. 10.5).

Лапласиан - .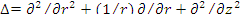

Граничные условия:

Ф(R_э,z)=0; Ф(r,±H_э/2)=0,

где R _э = R + d _э ; H _э = H +2 d _э ; R-радиус цилиндра; Н— высота цилиндра.

Решение находится методом разделения пере­менных. Функция плотности потока нейтронов Ф(r , z )  представляется в виде:

Ф(r , z )= P ( r ) Z ( z )

Подстановка ее в уравнение реактора приводит к двум уравнениям:

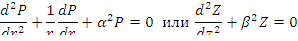
при условии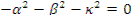

Первое уравнение с помощью замены х= κr приводится к уравнению Бесселя, решенному для бесконечного цилиндра, второе решено для параллелепипеда. Полным решением для конечного цилиндра является функция

 

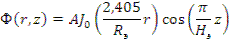
Геометрический параметр

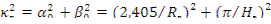
Константа А — плотность потока нейтронов в центре цилиндра, т.е. A=Ф(0,0). Коэффициент неравномерности

 

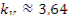
Минимальный критический объем

Минимальный критический объем из всех параллелепипедов, характери­зующихся разными соотношениями размеров а, b и с , имеет куб. Минималь­ный критический объем из всех цилиндров, характеризующихся разными соот­ношениями размеров H и R , имеет цилиндр с соотношением H / R ≈2.

В критическом состоянии геометрический параметр равен материальному,

т.е. 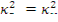 . Если состав среды задан, то, значит, задан  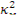. Материальный па­раметр определяется из решения критического уравнения (10.8) либо для доста­точно большого критического реактора рассчитывается по формуле (10.9). По­лученное значение материального параметра подставляется вместо геометриче­ского параметра в выражение его связи с размерами тела. Из этого выражения определяется минимальный критический размер и объем тела.

Минимальная критическая толщина бесконечного плоского реактора

а_э=π/κ_м.

Минимальный критический объем параллелепипеда

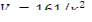
Минимальный критический радиус бесконечного кругового цилиндра

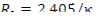
Минимальный критический объем конечного кругового цилиндра

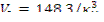
Минимальный критический объем шара

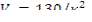
Наименьший критический объем из всех геометрических форм имеет шар.

 

11. КРИТИЧЕСКИЕ РАЗМЕРЫ ГОМОГЕННОГО РЕАКТОРА
С ОТРАЖАТЕЛЕМ

 

Влияние отражателя

 

       Добавление к поверхности активной зоны слоя материала (отражателя) при-
водит к тому, что часть нейтронов, выходящих из активной зоны, возвращается
обратно. Доля отражающихся нейтронов определяется величиной альбедо отражателя. При этом уменьшается утечка нейтронов из активной зоны. Если без
отражателя реактор - критический, то с отражателем он будет надкритическим.
Чтобы реактор с отражателем оставался критическим, надо уменьшить размеры
активной зоны. Поэтому критические размеры активной зоны реактора с отражателем всегда меньше, чем соответствующие размеры без отражателя.

       Распределение нейтронов у границы раздела формируется перетечками из
одной среды в другую. Вблизи границы нарушается пропорциональность потоков быстрых и тепловых нейтронов, поскольку отражателями служат, как правило, материалы с малым сечением поглощения нейтронов и иными, чем в активной зоне, диффузионными свойствами. При этом переменные r и Е в функции Ф(r,E) не разделяются.

       По мере удаления от границы в глубину активной зоны влияние отражателя
уменьшается и распределение нейтронов по пространству и энергии приближается к форме, зависящей только от параметров активной зоны. Такое распределение называется асимптотическим.

       Пространственно-энергетическое распределение нейтронов в реакторе с отражателем определяется приближенно: диапазон энергий нейтронов разбивается на несколько интервалов, рассматривается диффузия каждой группы ней-
тронов с неизменной энергией - средней энергией в пределах каждого интервала. При этом решается система уравнений, в которой плотность потока нейтронов зависит только от пространственной переменной.

       Для иллюстрации многих свойств реакторов с отражателем и оценки масштаба эффектов отражателя используются одногрупповое и двухгрупповое.