Нагрузкой
Пример 1. Раскрыть статическую неопределимость и построить эпюру изгибающих моментов для рамы, показанной на рис. 27.
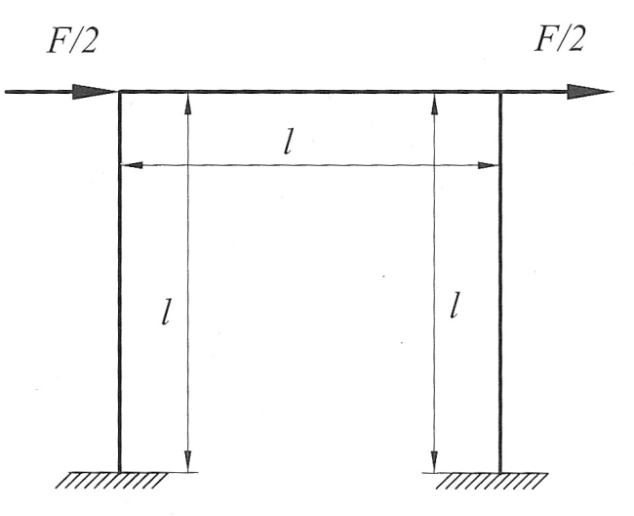
Рис. 27
Решение.
Определяем степень статической неопределимости.
Разрезаем раму по оси симметрии, получаем две половины рамы. Прикладываем внутренние силовые факторы к обеим половинам рамы. Их шесть: две продольные силы, две поперечные силы и два изгибающих момента (рис. 28, а, б). Данная рама три раза статически неопределимая, так как имеем 6 неизвестных и только три независимых уравнения статики:
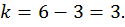
Рама симметричная и нагружена кососимметрично расположенными силами. При кососимметричной внешней нагрузке обращаются в нуль симметричные силовые факторы (рис. 28, в), т.е. продольные силы (  и изгибающие моменты
и изгибающие моменты 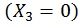 , а также коэффициенты
, а также коэффициенты 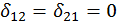 ,
, 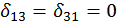 ,
, 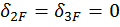 . Взамен трех уравнений получаем одно:
. Взамен трех уравнений получаем одно:
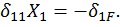
Вычисляем коэффициенты канонических уравнений по способу Верещагина.
Построим эпюры изгибающего момента  от внешней нагрузки для первой половины рамы (рис. 29, а).
от внешней нагрузки для первой половины рамы (рис. 29, а).
Составим выражения для изгибающих моментов на каждом участке.
Первый участок: 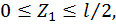
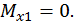
Второй участок: 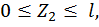
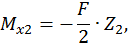
при 
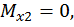
при 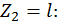
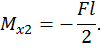
Построим эпюры изгибающего момента  от внешней нагрузки для второй половины рамы (рис. 29, б).
от внешней нагрузки для второй половины рамы (рис. 29, б).
Составим выражение для изгибающих моментов на каждом участке.
Первый участок: 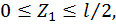
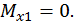
Второй участок: 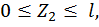
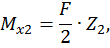
при 
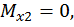
при 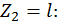
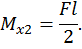
Построим эпюры изгибающего момента  от единичной нагрузки
от единичной нагрузки 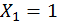 (единичную эпюру, рис. 29, в) для первой половины рамы.
(единичную эпюру, рис. 29, в) для первой половины рамы.
Составим выражения для изгибающих моментов на каждом участке.
Первый участок: 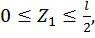
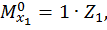
при 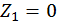 :
:
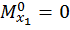 ,
,
при 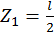 :
:
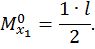
Второй участок: 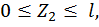
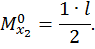
Построим эпюры изгибающего момента  от единичной нагрузки
от единичной нагрузки 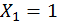 (единичную эпюру, рис. 29, г) для второй половины рамы.
(единичную эпюру, рис. 29, г) для второй половины рамы.
Составим выражение для изгибающих моментов на каждом участке.
Первый участок: 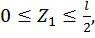
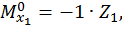
при 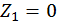 :
:
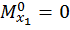 ,
,
при 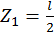 :
:
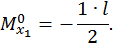
Второй участок: 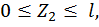
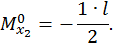
Коэффициент 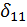 определяем «перемножением» эпюры
определяем «перемножением» эпюры 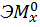 самой на себя (см. рис. 29 в, г).
самой на себя (см. рис. 29 в, г).
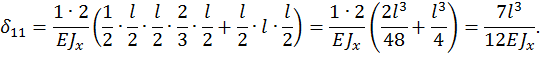
Грузовой коэффициент 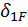 находим «перемножением» грузовой эпюры
находим «перемножением» грузовой эпюры 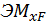 (рис. 29, а, б) на эпюру от единичной нагрузки
(рис. 29, а, б) на эпюру от единичной нагрузки 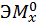 (рис. 29, в, г).
(рис. 29, в, г).
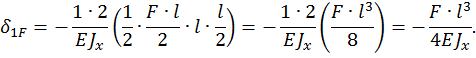
Определяем неизвестную 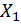 , решая каноническое уравнение
, решая каноническое уравнение
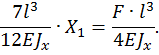
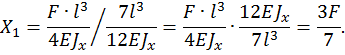
Таким образом, статическая неопределимость раскрыта.
Построим эпюры изгибающего момента для первой половины заданной рамы (рис. 30, а).
Составим выражение для изгибающих моментов на каждом участке:
Первый участок: 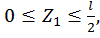
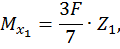
при 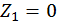 :
:
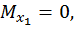
при 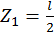 :
:
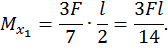
Второй участок: 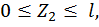
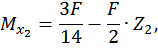
при 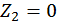 :
:
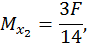
при 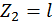 :
:
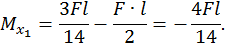
Построим эпюры изгибающего момента для второй половины заданной рамы (рис. 30, б).
Составим выражение для изгибающих моментов на каждом участке.
Первый участок: 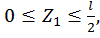
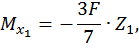
при 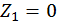 :
:
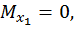
при 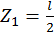 :
:
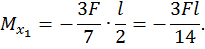
Второй участок: 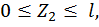
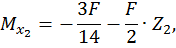
при 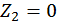 :
:
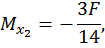
при 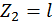 :
:
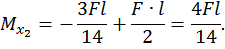
Объединяем обе эпюры, получившаяся эпюра является эпюрой изгибающих моментов для заданной рамы (рис. 30, в).
Максимальный изгибающий момент возникает в левой и правой опорах:
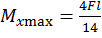 .
.
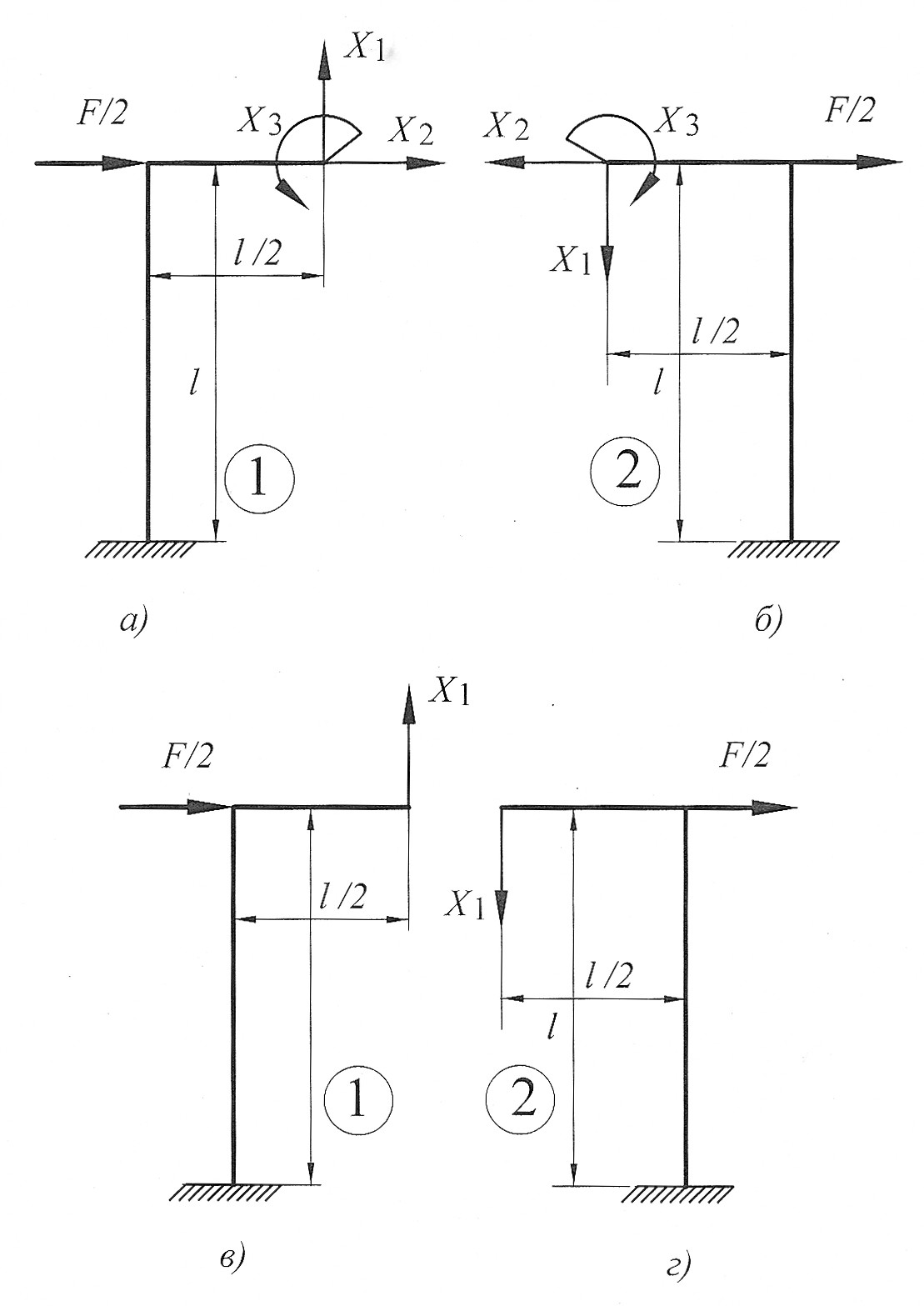 Рис. 28
Рис. 28
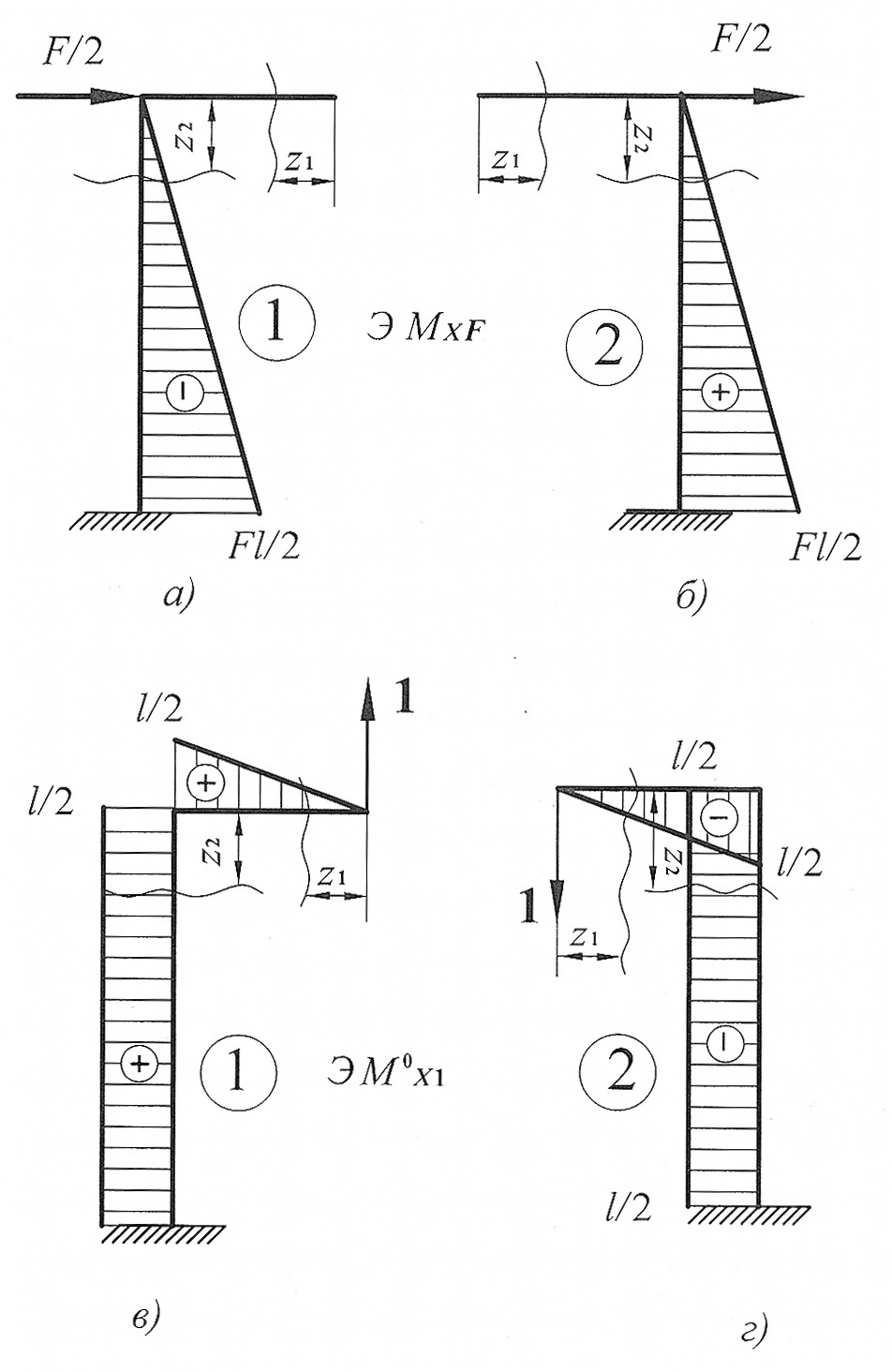
Рис. 29
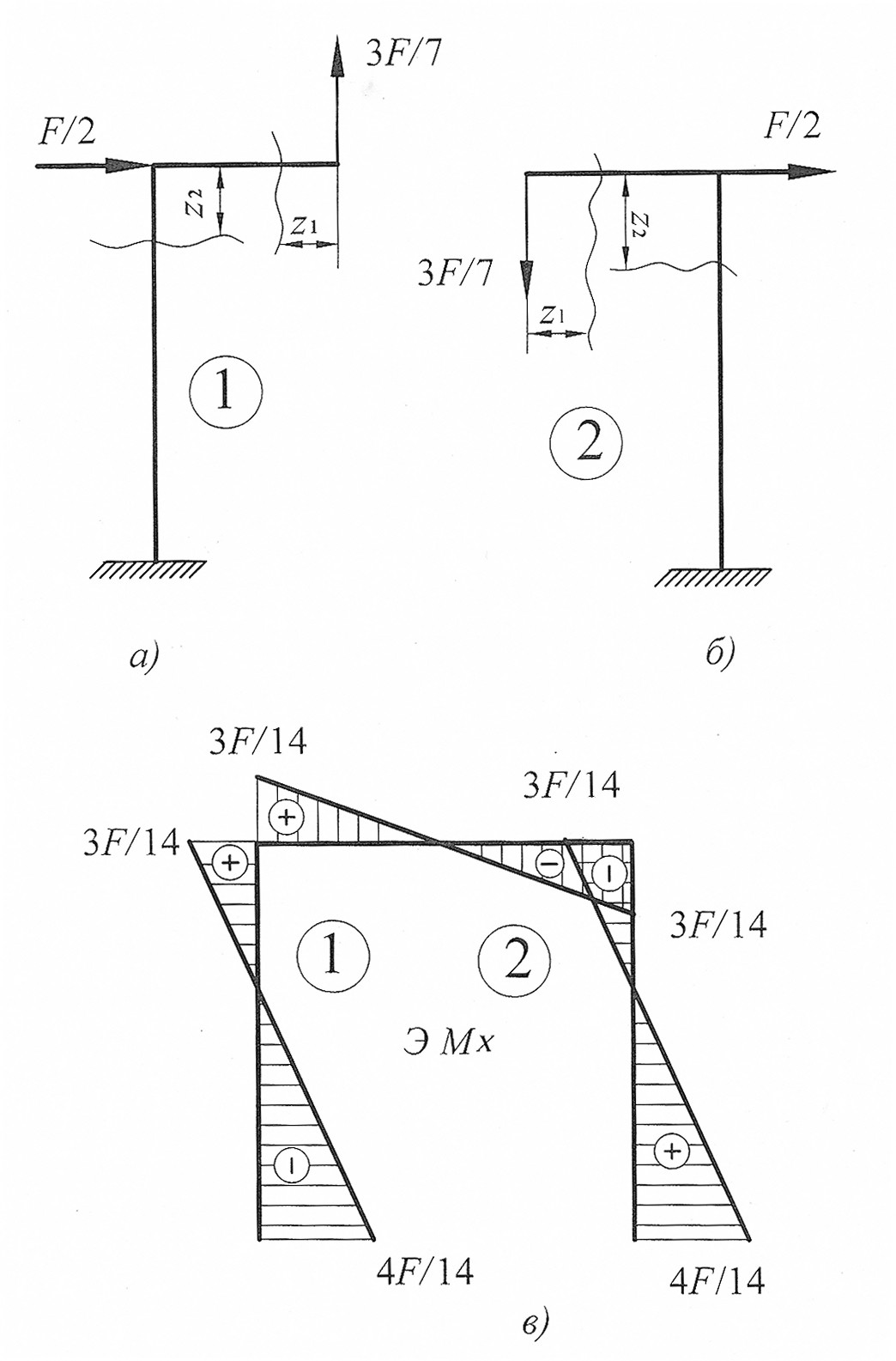 Рис. 30
Рис. 30
ЗАДАЧИ ДЛЯ ПРОВЕРКИ СТУДЕНТАМИ СТЕПЕНИ УСВОЕНИЯ МАТЕРИАЛА РАЗДЕЛА «СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ»
Задача 1
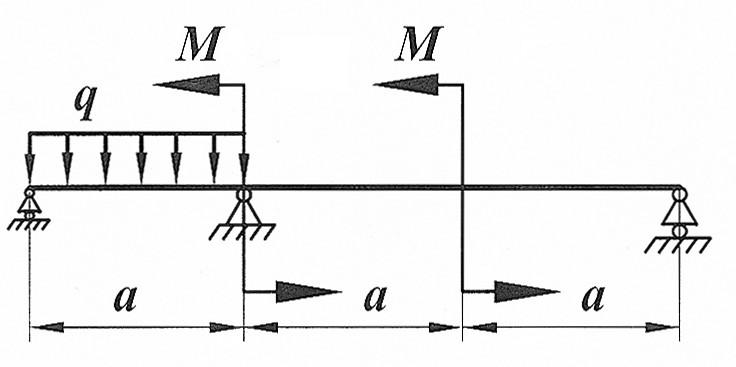
Раскрыть статическую неопределимость, построить эпюры 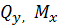 изображенной на рисунке балки. изображенной на рисунке балки.
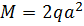 , ,

|
|
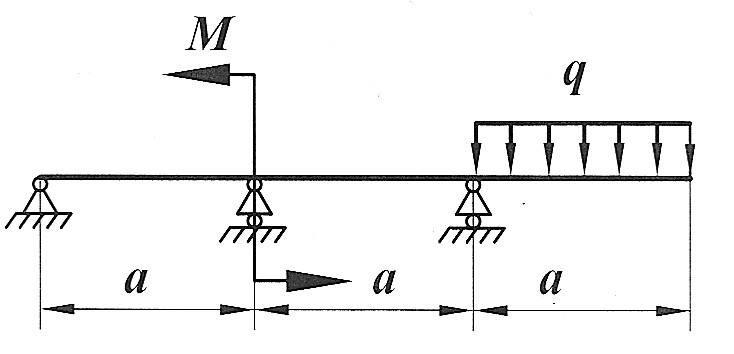
Задача 2
Раскрыть статическую неопределимость, построить эпюры 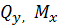 изображенной на рисунке балки. изображенной на рисунке балки.
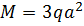 , ,

|
|
Задача 3
Раскрыть статическую неопределимость, построить эпюры 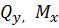 изображенной на рисунке балки. изображенной на рисунке балки.
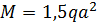 , ,

|
|
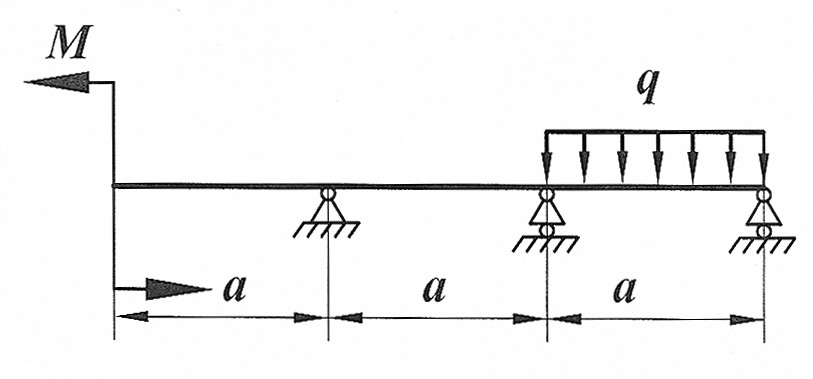
Задача 4
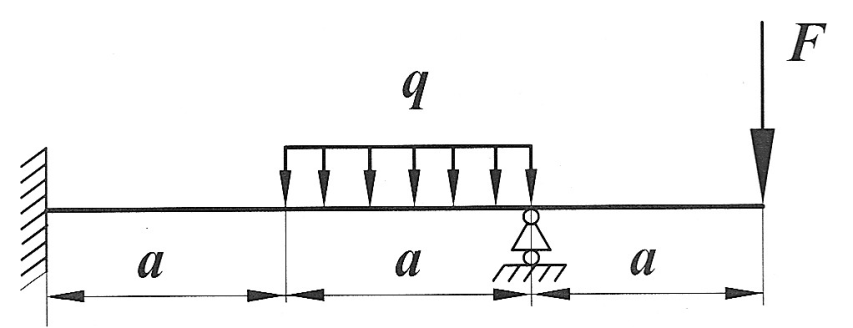
|
Раскрыть статическую неопределимость, построить эпюры 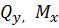 изображенной на рисунке балки. изображенной на рисунке балки.
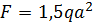 , ,

|
Задача 5
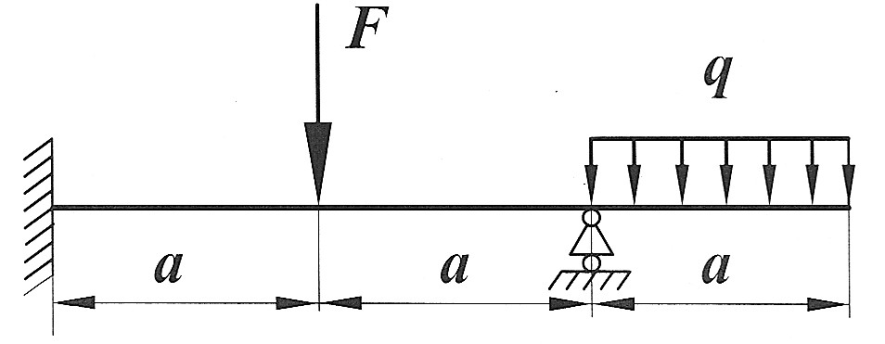
|
Раскрыть статическую неопределимость, построить эпюры 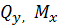 изображенной на рисунке балки. изображенной на рисунке балки.
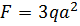 , ,

|
Задача 6
|
Раскрыть статическую неопределимость, построить эпюры 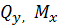 изображенной на рисунке балки. изображенной на рисунке балки.
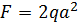 , ,

|
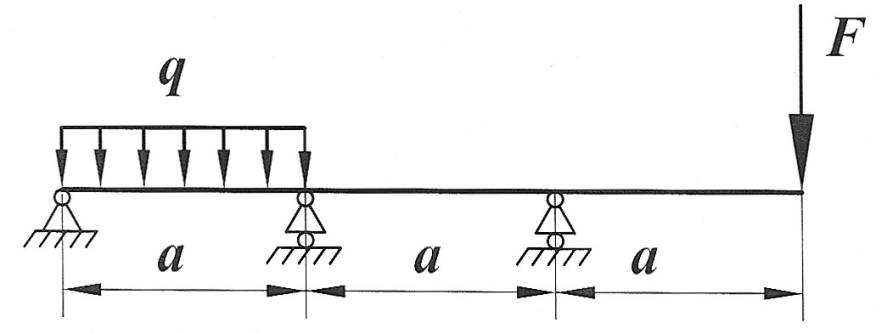
Задача 7
Раскрыть статическую неопределимость, построить эпюры 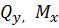 . Составить условие прочности. . Составить условие прочности.
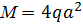 , ,

|
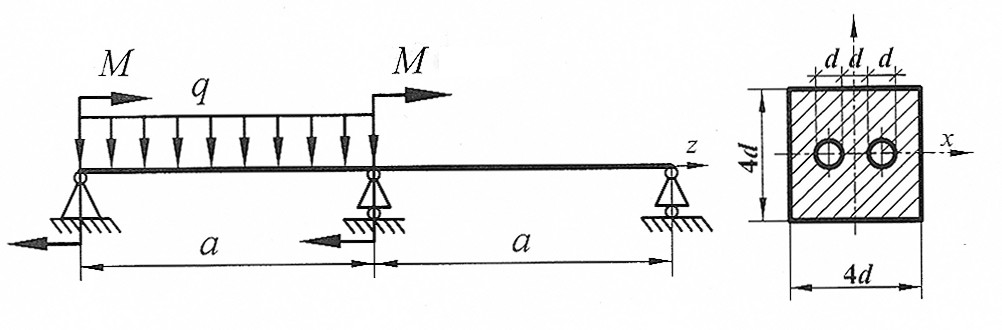
|
Задача 8
Раскрыть статическую неопределимость, построить эпюры 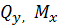 изображенной на рисунке балки. Составить условие прочности. изображенной на рисунке балки. Составить условие прочности.
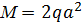 , ,

|
|
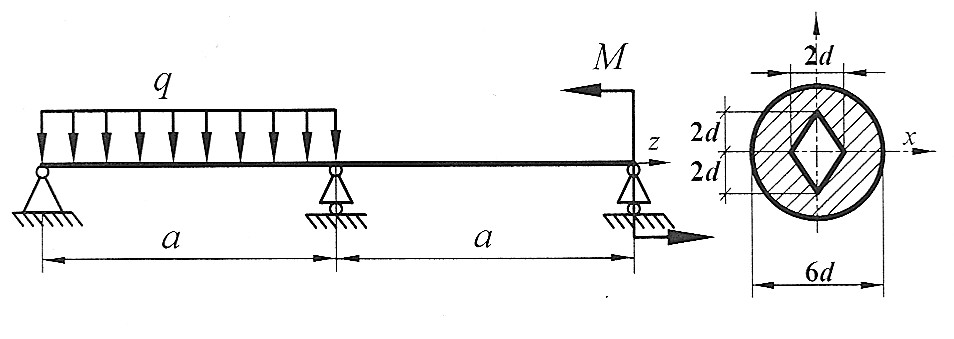
Задача 9
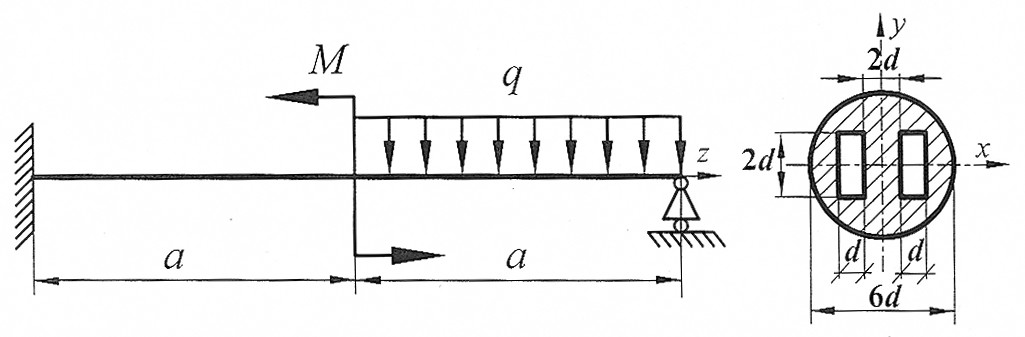
Раскрыть статическую неопределимость, построить эпюры 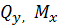 изображенной на рисунке балки. Составить условие прочности. изображенной на рисунке балки. Составить условие прочности.
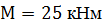 , ,
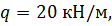
 , ,

|
|
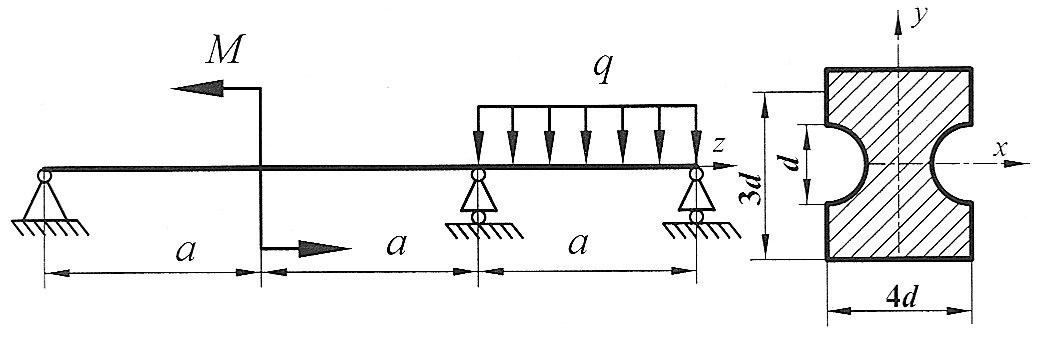
Задача 10
|
Раскрыть статическую неопределимость, построить эпюры 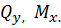 Составить условие прочности. Составить условие прочности.
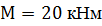 , ,
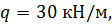
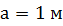 , , 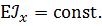
|
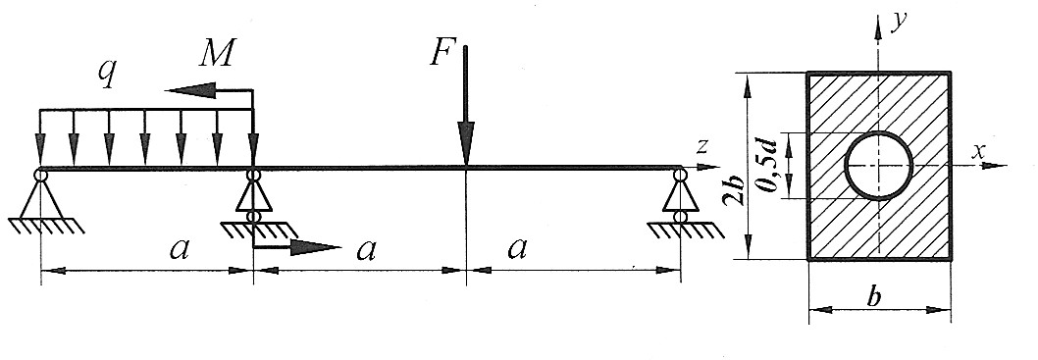
Задача 11
|
Раскрыть статическую неопределимость, построить эпюры 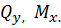 Составить условие прочности. Составить условие прочности.
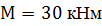 , ,
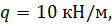
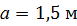 , , 
|
Задача 12

|
Раскрыть статическую неопределимость, построить эпюры 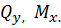 Составить условие прочности. Составить условие прочности.
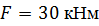 , ,
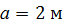 , ,

|
Задача 13
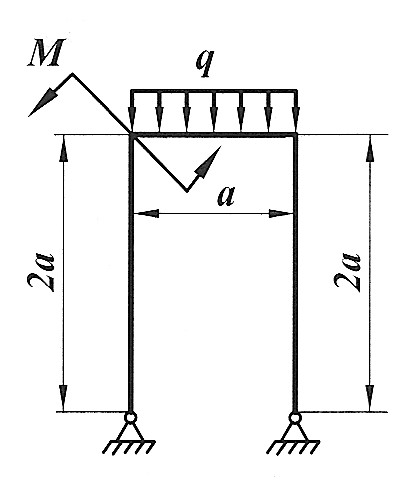
Раскрыть статическую неопределимость, построить эпюры 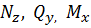 изображенной на рисунке рамы. изображенной на рисунке рамы.
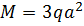 , ,

| 
|
Задача 14
Раскрыть статическую неопределимость, построить эпюры 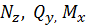 изображенной на рисунке рамы. изображенной на рисунке рамы.
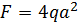 , ,

|
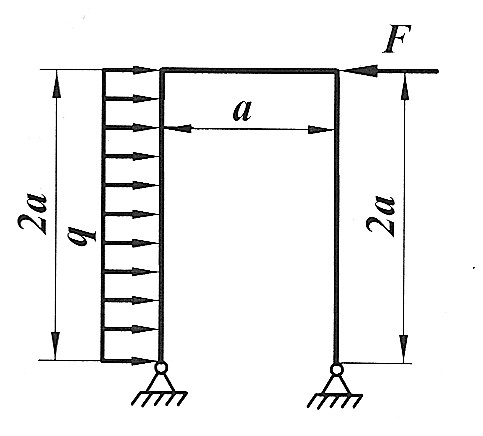
|
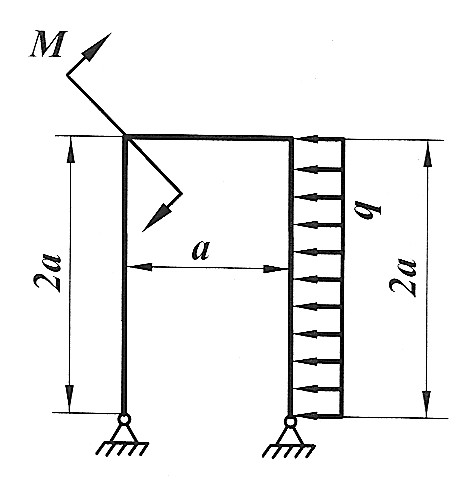
Задача 15
Раскрыть статическую неопределимость, построить эпюры 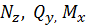 изображенной на рисунке рамы. изображенной на рисунке рамы.
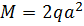 , ,

| 
|
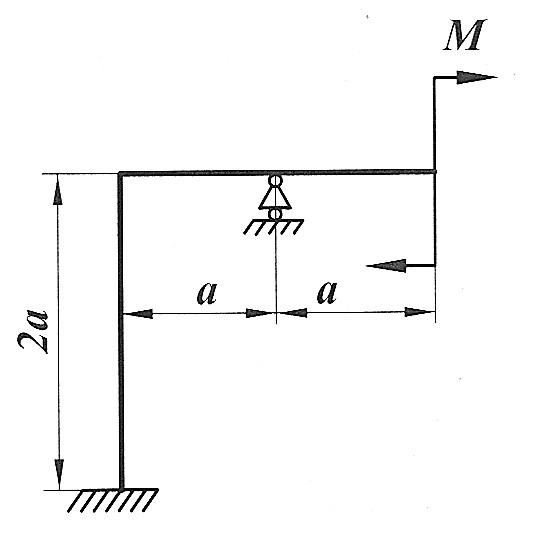
Задача 16
|
Раскрыть статическую неопределимость, построить эпюры 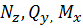 изображенной на рисунке рамы. изображенной на рисунке рамы.
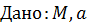 , ,

|
Задача 17
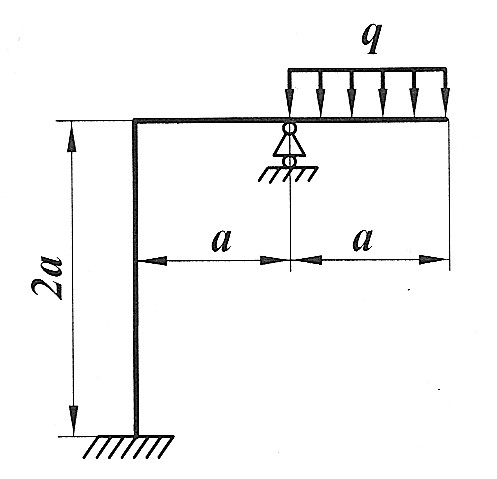
| Раскрыть статическую неопределимость, построить эпюры 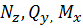 изображенной на рисунке рамы. изображенной на рисунке рамы.
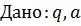 , ,

|
Задача 18
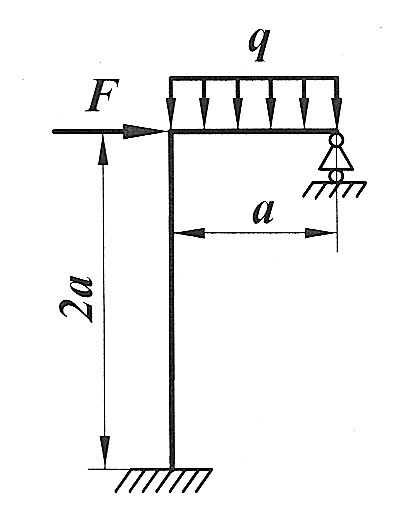
| Раскрыть статическую неопределимость, построить эпюры 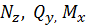 изображенной на рисунке рамы. изображенной на рисунке рамы.
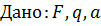 , ,

|
Задача 1 9
Раскрыть статическую неопределимость, построить эпюры 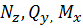 изображенной на рисунке рамы.
Из условия прочности определить размеры поперечного сечения. Найти горизонтальное перемещение сечения С и угол поворота сечения D изображенной на рисунке рамы.
Из условия прочности определить размеры поперечного сечения. Найти горизонтальное перемещение сечения С и угол поворота сечения D
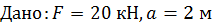 , , 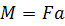 , , 

| 
|
Задача 20
Раскрыть статическую неопределимость, построить эпюры 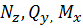 изображенной на рисунке рамы.
Составить условие прочности. изображенной на рисунке рамы.
Составить условие прочности.
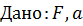 , , 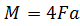 , d . , d .

| 
|
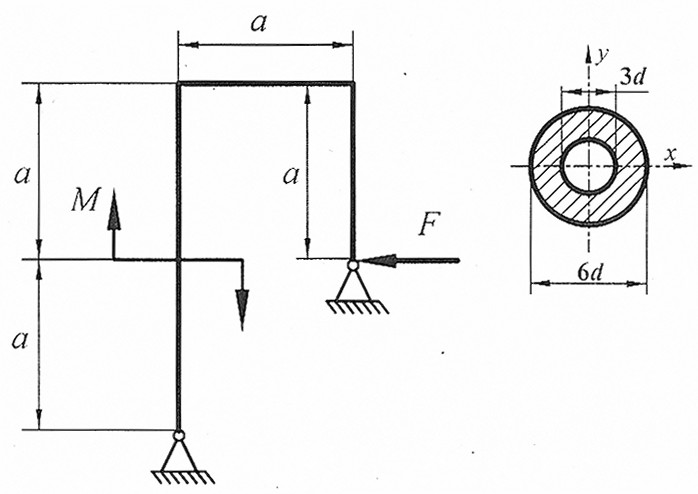
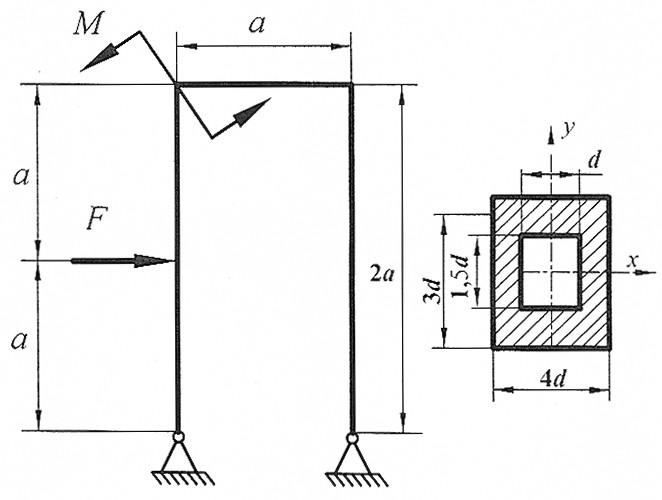
Задача 21
Раскрыть статическую неопределимость, построить эпюры 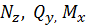 изображенной на рисунке рамы.
Составить условие прочности. изображенной на рисунке рамы.
Составить условие прочности.
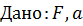 , , 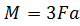 , d . , d .

| 
|
Задача 22
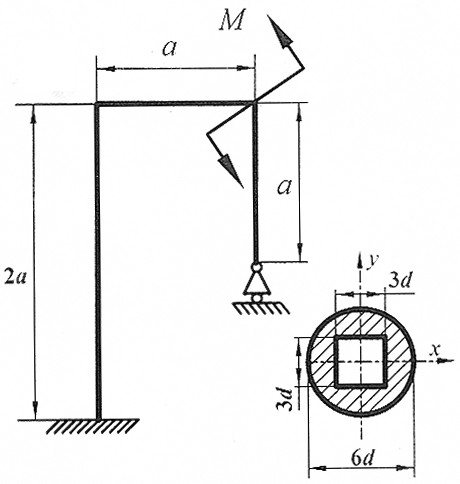
| Раскрыть статическую неопределимость, построить эпюры 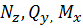 изображенной на рисунке рамы.
Составить условие прочности. изображенной на рисунке рамы.
Составить условие прочности.
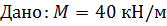 , ,
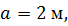 d = 2 см. d = 2 см.

|
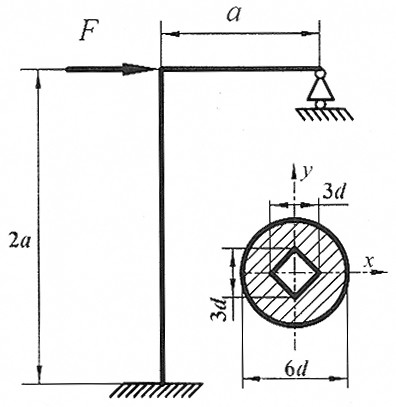
Задача 2 3
|
Раскрыть статическую неопределимость, построить эпюры 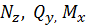 изображенной на рисунке рамы.
Составить условие прочности. изображенной на рисунке рамы.
Составить условие прочности.
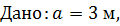 d = 3 см. d = 3 см.

|
Задача 2 4
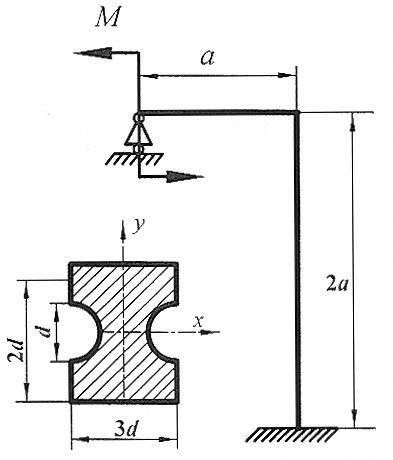
| Раскрыть статическую неопределимость, построить эпюры 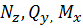 изображенной на рисунке рамы.
Составить условие прочности. изображенной на рисунке рамы.
Составить условие прочности.
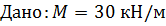 , , 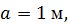 d = 3 см. d = 3 см.

|
Задача 25
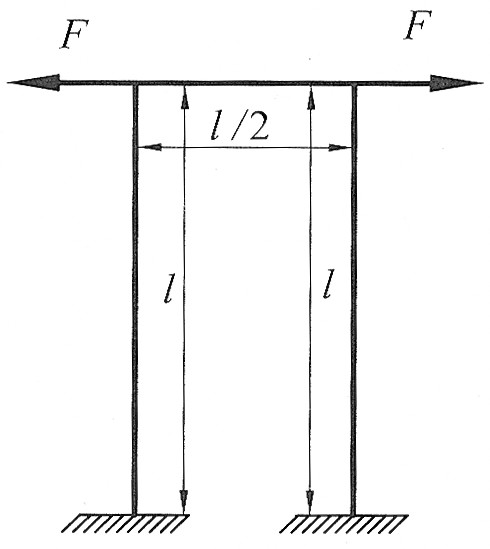
Раскрыть статическую неопределимость, построить эпюру изгибающих моментов изображенной на рисунке рамы.
Дано: 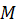 , , 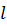 . .

| 
|
Задача 2 6
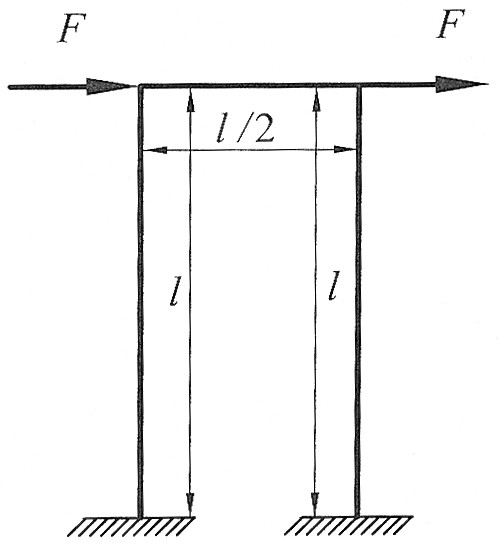
Раскрыть статическую неопределимость, построить эпюру изгибающих моментов изображенной на рисунке рамы.
Дано: 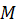 , , 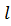 . .

| 
|
Задача 2 7
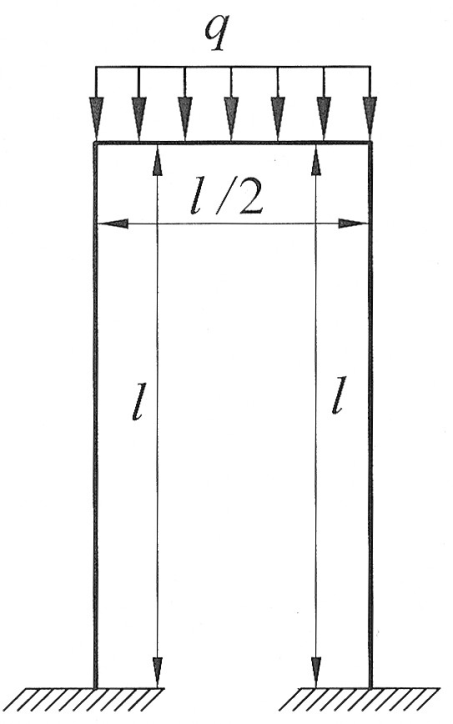
Раскрыть статическую неопределимость, построить эпюру изгибающих моментов изображенной на рисунке рамы.
Дано: 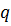 , , 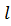 . .

| 
|
Задача 2 8
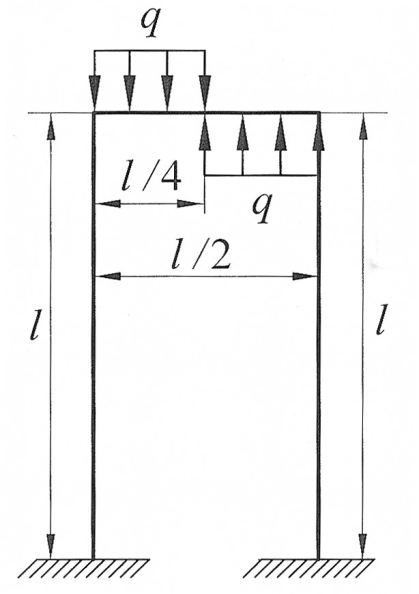
| Раскрыть статическую неопределимость, построить эпюру изгибающих моментов изображенной на рисунке рамы.
Дано: 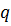 , , 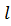 . .

|
Задача 29
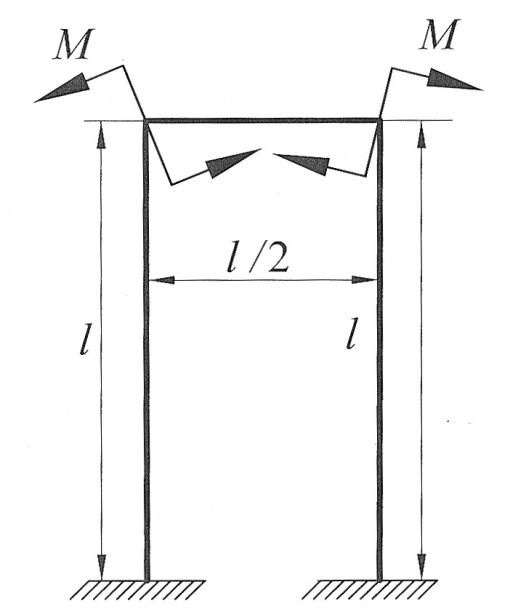
| Раскрыть статическую неопределимость, построить эпюру изгибающих моментов изображенной на рисунке рамы.
Дано: 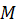 , , 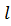 . .

|
Задача 30

| Раскрыть статическую неопределимость, построить эпюру изгибающих моментов изображенной на рисунке рамы.
Дано: 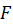 , , 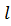 . .

|
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие деформации и перемещения возникают в балках, работающих на изгиб?
2. В чем состоит общая идея метода начальных параметров? Запишите универсальные уравнения для определения прогибов и углов поворота.
3. С помощью каких дифференциальных уравнений определяются перемещения при изгибе балок?
4. Какие методы используются для определения перемещений при изгибе балок?
5. Сколько неизвестных содержит выражение для прогибов при использовании метода начальных параметров
6. Какие типы опор применяются для соединения балок с основанием и какие реактивные усилия и моменты могут возникать в этих опорах?
7. Какие уравнения равновесия применяются для определения опорных реакций и как проверить правильность определения опорных реакций?
8. В каких случаях нельзя использовать универсальные уравнения метода начальных параметров для определения перемещений в балках?
9. Эпюры каких внутренних усилий используются при определении перемещений при изгибе методом Мора?
10. Какой физический смысл интегралов Мора?
11. Как выбираются направления действия единичных силы или момента при использовании метода Мора? Как определяется знак перемещений?
12. Укажите какие трудности можно отнести к недостаткам определения перемещений при помощи интеграла Мора?
13. Как можно вычислить интегралы Мора при определении перемещений в прямых стержнях с постоянной жёсткостью?
14. Для каких балок вместо непосредственного вычисления интеграла Мора можно использовать графоаналитический прием вычисления по правилу Верещагина?
15. В каком случае при вычислении интегралов Мора нельзя использовать правило А.К.Верещагина?
16. На какие простые фигуры можно разбить эпюры изгибающих моментов, построенных от внешней нагрузки, представляющих собой:
16.1.”однозначную” трапецию-трапецию, расположенную по одну сторону от нулевой оси;
16.2. “разнозначную” трапецию-трапецию, расположенную по обе стороны от нулевой оси;
16.3. “однозначную” трапецию, ограниченную сверху параболой;
16.4. “разнозначную” трапецию, ограниченную сверху параболой.
17. Какие системы называются статически неопределимыми?
18. Что называется степенью статической неопределимости?
19. Какая система называется геометрически неизменяемой?
20. Что представляет из себя основная и эквивалентная системы?
21. Что означают величины 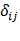 и
и 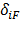 и как они определяются?
и как они определяются?
22. Напишите систему канонических уравнений?
23. Каким способом можно построить эпюры M, Q, N в заданной статически неопределимой системе после того, как определены неизвестные 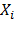 ?
?
24. На чем основана и как производится деформационная проверка суммарной эпюры изгибающих моментов?
25. Как производится определение перемещений в статически неопределимых системах?
ЗАКЛЮЧЕНИЕ
В методическом пособии кратко изложены теоретические основы определения перемещений, возникающих при изгибе балок и плоских стержневых систем по трем, наиболее широко используемым на практике, методам: методу начальных параметров, методу Мора, и способу Верещагина, а также их использование при раскрытии статической неопределимости методом сил. Для облегчения студентами применения правила «перемножения» эпюр по Верещагину приведены примеры разбиения сложных эпюр изгибающих моментов на простые фигуры с указанием положения центра их тяжести.
С целью лучшего усвоения студентами материала по каждому разделу разработан порядок решения задачи представлен подробный пример расчета.
Подробно рассмотрена задача по раскрытию статической неопределимости плоской стержневой системы (рамы) методом сил, а также особенности ее решения при использовании свойств симметрии.
В приложениях методического пособия приведены некоторые стандартные данные по определению геометрических характеристик плоских сечений (площади, осевых моментов инерции и сопротивления), а также таблицы прокатных профилей (двутавры, швеллеры) основных геометрических форм сечений стержней, используемых при проектировании инженерных конструкции.
По мнению авторов, данное методическое пособие может оказать студентам значительную помощь при изучении ими дисциплин «Сопротивление материалов» и «Техническая механика», а также при выполнении самостоятельных расчетных работ.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Феодосьев, В.И. Сопротивление материалов. – М.: Наука, 1999. – 560 с.
2. Беляев, Н.М. Сопротивление материалов. – М.: Наука, 1976. – 552 с.
3. Афанасьев, А.М. Лабораторный практикум по сопротивлению материалов / A.M. Афанасьев, В.А. Марьин. – М.: Наука, 1975. – 269 с.
4. Копнов, В.А. Сопротивление материалов: Руководство для решения задач и выполнения лабораторных и расчетно-графических работ / В.А. Копнов, С.Н. Кривошапко. – М.: Высш. шк., 2009. – 351 с.
5. Дарков, А.В. Сопротивление материалов / А.В. Дарков, Г.С. Шпиро. – М.: Высшая школа, 1984.
6. Макаров, Е.Г. Сопротивление материалов на базе Mathcad. – СПб.: БХВ-Петербург, 2004. – 512 с.
7. Александров А.В. Сопротивление материалов: / А.В. Александров, В.Д. Потапов, Б.П. Державин. – 2-е изд., испр. – М.: Высш. шк., 2000. – 560 с.
Приложение А. Двутавры стальные горячекатаные
Сортамент по ГОСТ 8239–89
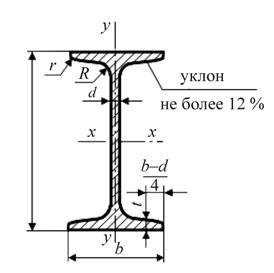
Номер балки
h
b
d
t
Площадь сечения, см2
Масса
1 м, кг
Дата: 2019-03-05, просмотров: 499.