Статической неопределимости

Положим, имеется некоторая симметричная, в геометрическом смысле, рама (рис. 24, а). Ее правую часть можно рассматривать как зеркальное отображение левой части относительно плоскости симметрии. При расчете таких рам оказывается возможным упростить решение задачи и уменьшить число искомых силовых факторов.

Рассмотрим случаи нагружения рамы симметричной (рис. 24, б) и кососимметричной (рис. 24, в) нагрузками. Под симметричной нагрузкой будем понимать такую нагрузку, при которой все внешние силы, приложенные к правой части рамы, являются зеркальным отображением сил, приложенных к ее левой части (см. рис. 24, б). Под кососимметричной, или антисимметричной, нагрузкой будем понимать такую нагрузку, при которой силы, приложенные к правой половине рамы, также являются зеркальным отображением сил, приложенных к ее левой половине, но противоположны им по знаку (см. рис. 24, в).

Рис. 24

Аналогично классифицируем и внутренние силовые факторы. Рассмотрим для этого некоторое произвольное сечение рамы, в котором возникает шесть силовых факторов. В правой и левой частях бруса (рис. 25) внутренние силы и моменты равны. Посмотрим, какие из шести силовых факторов образуют зеркальное отображение относительно плоскости сечения. Такими оказываются три фактора: два изгибающих момента и нормальная сила. Будем их называть симметричными внутренними факторами. Крутящий момент и обе поперечные силы в принятой терминологии должны быть названы кососимметричными факторами. Каждый из них противоположен по знаку зеркальному отображению взаимного фактора.

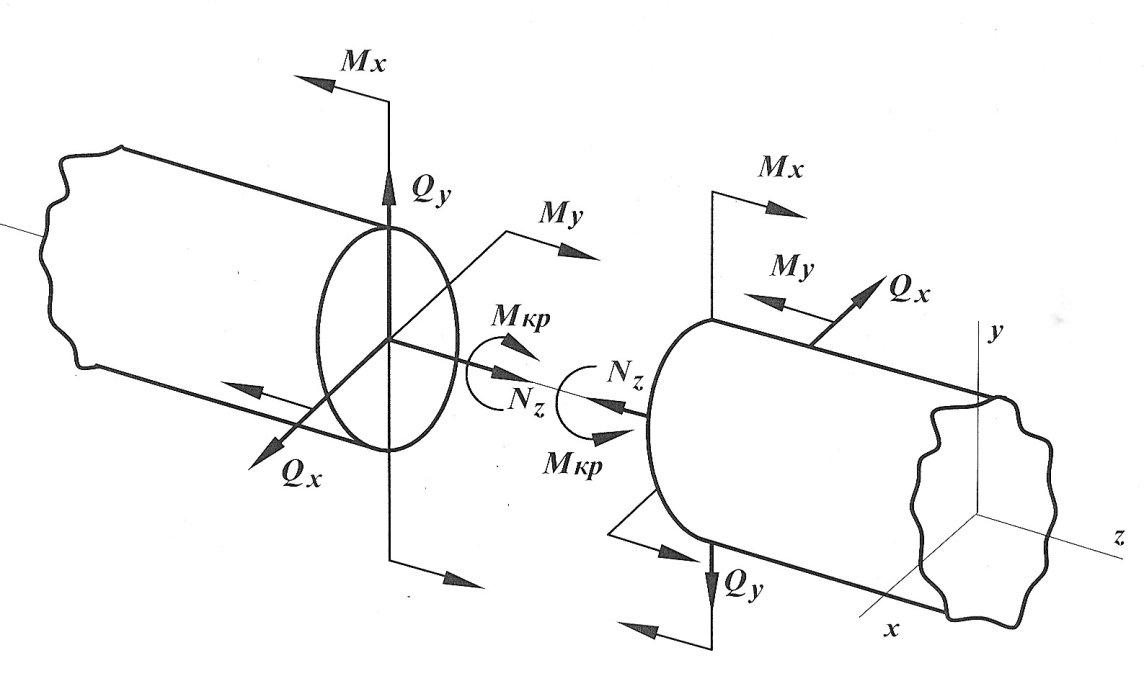
Рис. 25

Обратимся к симметричной раме, например, показанной на рис. 24, б, и выберем основную систему, разрезая раму по плоскости симметрии (рис. 26).

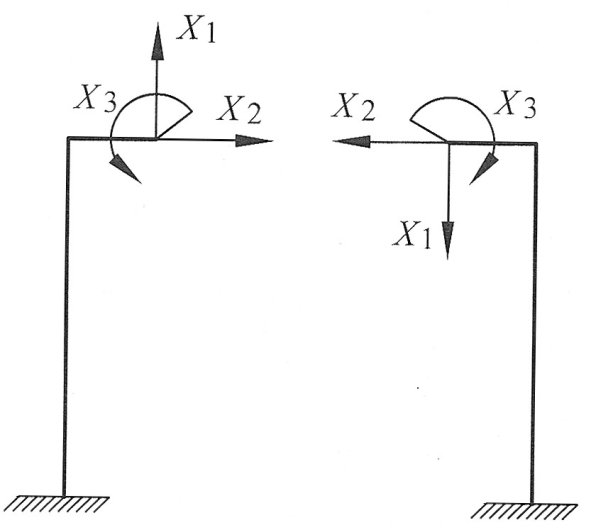
Рис. 26

Обозначим через 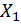 кососимметричный, а через  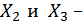симметричные силовые факторы и выпишем систему канонических уравнений. В данном случае их будет три:

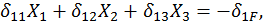
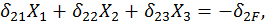                        (23)

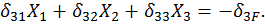
Прежде всего необходимо отметить, что независимо от характера внешней нагрузки все коэффициенты 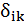, у которых один индекс принадлежит симметричному, а второй кососимметричному силовому фактору, равны нулю, то есть 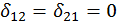,  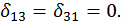Кроме того, если предположить, что внешняя нагрузка F симметричная, то дополнительно  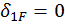и 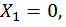тогда система уравнений (23) примет вид

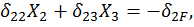
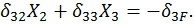                                   (24)

Если же внешняя нагрузка кососимметричная, то коэффициенты 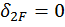 и 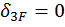, а также  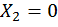и 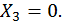 В этом случае система уравнений примет вид:

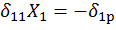.                                    (25)

Происходит это потому, что в симметричной раме не возникает взаимных кососимметричных перемещений под действием симметрич-ных нагрузок. Точно так же не возникает симметричных перемещений под действием кососимметричных факторов. Сказанное становится еще более очевидным, если учесть, что в рассматриваемой системе эпюра изгибающих моментов от кососимметричных факторов будет кососим-метричной, а от симметричных факторов - симметричной. При перемно-жении таких эпюр, естественно, получим нуль, в то время как перемно-жение кососимметричной эпюры на кососимметричную и симметричной на симметричную эпюру, дает результат, отличный от нуля.

Пример расчета симметричной статически