Основные положения

Стержневые системы, в том числе и рамы, можно разделить на статически определимые и статически неопределимые. Любая стержневая система становится статически неопределимой, если на нее наложено связей больше, чем это необходимо для ее равновесия как жесткого целого.

Свободное тело в плоскости имеет три степени свободы. Чтобы тело находилось в равновесии, на него должны быть наложены три связи, называемые необходимыми. Связи, наложенные на тело сверх необходимых, называются дополнительными или «лишними». Число «лишних» связей, наложенных на систему, определяет ее степень статической неопределимости. Различают внешние и внутренние связи. Внешние связи накладывают в опорах системы и обеспечивают равновесие системы в целом. Внутренние связи обеспечивают равновесие любой произвольно выделенной части системы, то есть препятствуют взаимным перемещениям смежных сечений. В плоской раме в каждом сечении имеются три внутренние связи, препятствующие трем взаимным перемещениям: продольному, поперечному, угловому.

Усилия, возникающие во внешних связях, называются опорными реакциями, а во внутренних связях – внутренними силовыми факторами.

В статически определимых системах все реакции и внутренние силовые факторы определяются с помощью уравнений равновесия статики. В статически неопределимых системах для определения указанных величин недостаточно уравнений статики, необходимы еще дополнительные уравнения.

Расчет статически неопределимой рамы или балки начинается с определения степени статической неопределимости. Степень статической неопределимости k – это разность между числом неизвестных n (опорных реакций или внутренних силовых факторов) и числом независимых уравнений статики для заданной системы m:

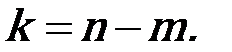
Для любой плоской системы число независимых уравнений статики равно 3.

Общим методом раскрытия статической неопределимости стержневых систем в машиностроении является метод сил. По методу сил расчет статически неопределимой системы заменяется расчетом основной системы, получаемой из заданной путем отбрасывания «лишних» связей. Реакции отброшенных связей заменяются неизвестными силами или моментами, обозначенными буквой Х. (Если связь препятствует линейному перемещению, она заменяется силой, угловому – моментом). Основная система – это статически определимая, кинематически неизменяемая система. Для статически неопределимой системы можно получить несколько основных систем в зависимости от удаленных связей.

В заданной системе перемещения по направлению отброшенных связей ограничены, в основной системе эти перемещения возможны. Для того чтобы основная система была эквивалентна заданной, необходимо, чтобы перемещения в основной системе по направлению отброшенных связей были соответственно равны перемещениям в заданной системе. Исходя из этого условия составляются дополнительные уравнения (уравнения перемещений). Если отбрасываемые связи жесткие, то перемещения по их направлению в заданной системе равны нулю, и дополнительные уравнения можно записать в таком виде:

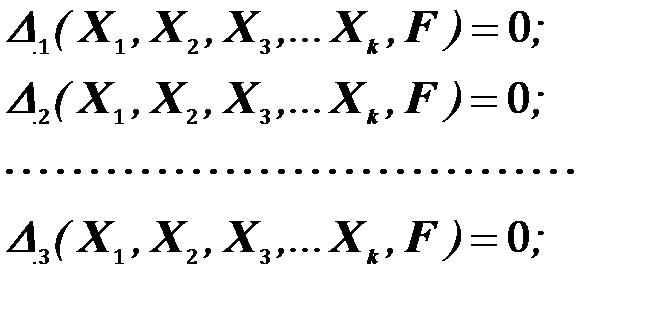                          (20)

где 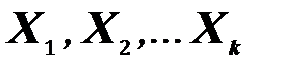  – реакции отброшенных связей;

    F – внешняя нагрузка в заданной системе;

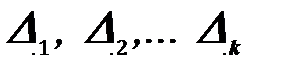    – перемещения в направлении отброшенных связей.

Пользуясь принципом независимости действия сил, перемещения 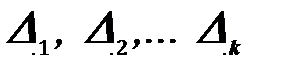 можно представить суммой перемещений от каждой нагрузки, и полученные выше уравнения принимают вид

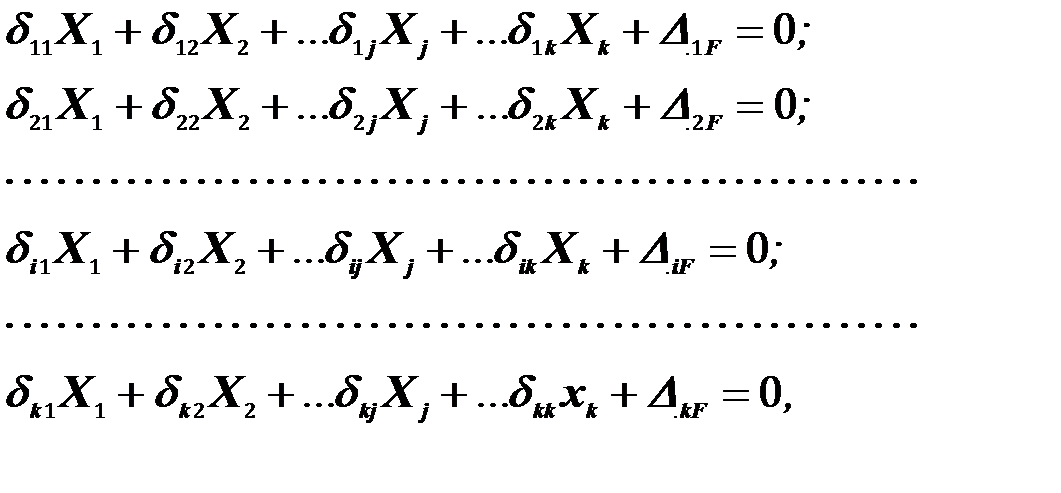  (21)

где 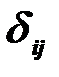 - перемещение точки приложения силы Х _i в направлении этой силы от силы Х _j=1;

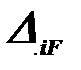- перемещение точки приложения силы Х _i в направлении этой силы от известной внешней нагрузки.

Приведенные уравнения (20) называются каноническими уравнениями метода сил. Количество их всегда равно степени статической неопределимости заданной системы. Для раскрытия статической неопределимости необходимо решить систему канонических уравнений, т.е. найти величины Х₁, Х_{2 …} Х _k . Для этого, очевидно, надо знать величину коэффициентов 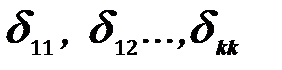   и свободных членов  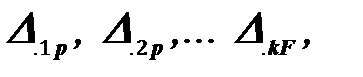входящих в канонические уравнения. Эти коэффициенты по физическому смыслу представляют собой перемещения, поэтому определить их можно в общем случае с помощью интегралов Максвелла-Мора.

Для плоской рамы, состоящей из прямолинейных стержней или балки, коэффициенты канонических уравнений можно вычислить по способу Верещагина.