Пример 1.
Для консольной балки (рис. 3) постоянной жесткости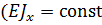 
) необходимо определить угол поворота 
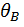и прогиб 
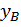на свободном конце.
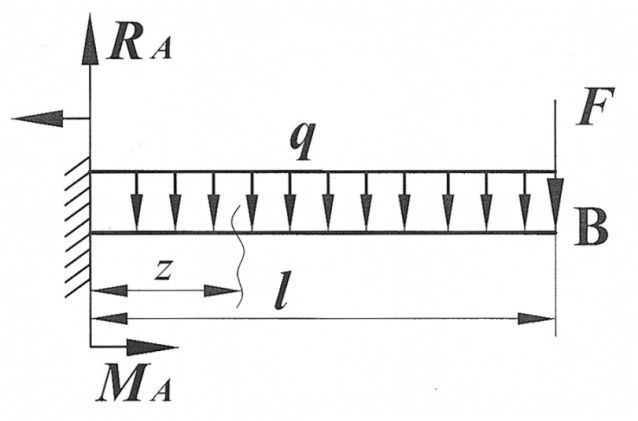
Рис. 3
Решение.
Для определения опорных реакций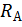 
и 
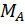составим два уравнения статики:
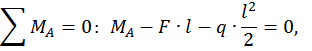
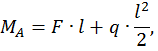
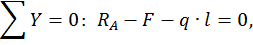
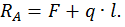
Запишем универсальное уравнение упругой линии балки для произвольного сечения с координатой z.
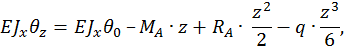
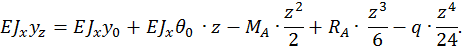
Учитывая, что 
и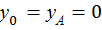 
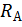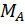и подставляя и в полученные уравнения, имеем:
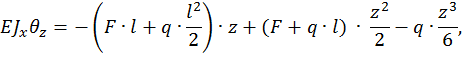
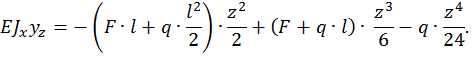
Для определения искомых перемещени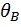й 
и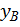 
в полученные уравнения необходимо подставить z=l , тогда:
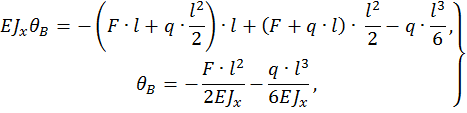
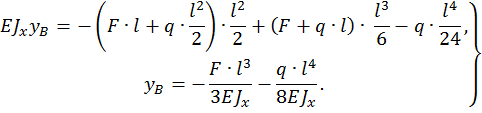
Пример 2.
Определить прогиб в сечении D, угол поворота на опоре B балки, изображенной на рис. 4, при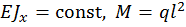 
.
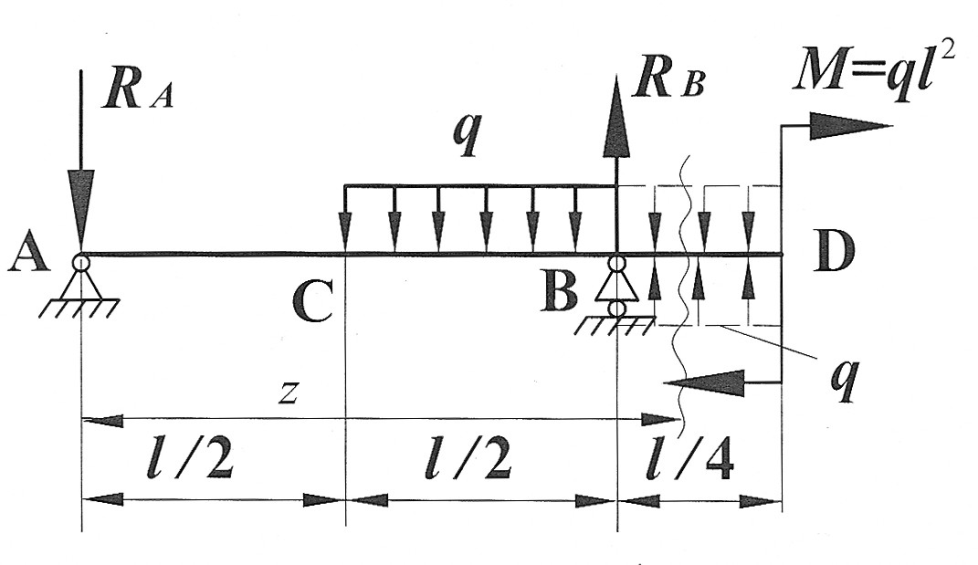
Рис. 4
Для определения реакций опор 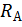и 
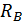составим два уравнения статики:
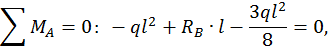
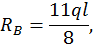
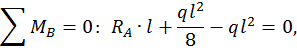
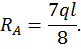
Для произвольного сечения с координатой z составим уравнение изогнутой оси балки. Поскольку распределенная нагрузка q прерывается, ее необходимо продолжить до конца балки, одновременно добавив такую же нагрузку по модулю, но противоположно направленную. Поскольку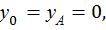 
имеем:
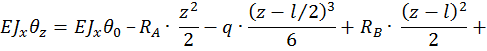
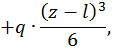
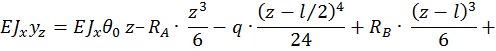
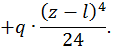
Для определения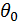 
используем условие, что при z = l , 
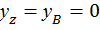, тогда угол поворота 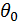равен
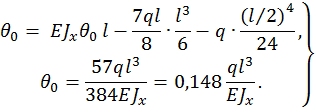
Угол поворота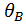 
находим, подставляя z = l , тогда:
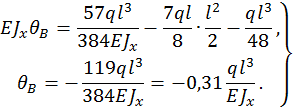
Находим прогиб в сечении D, для этого подставляем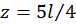 
:
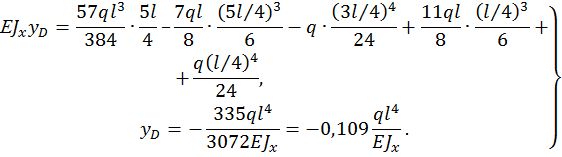
МЕТОД МОРА
Основные положения
В данном разделе рассмотрим общий метод определения перемещений (линейных и угловых), возникающих при прямом поперечном изгибе плоских стержневых систем, когда их оси могут быть не только прямыми, но и иметь некоторую малую кривизну и состоять из нескольких участков, имеющих непостоянную жесткость, то есть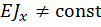 
.
Наиболее просто эти уравнения находятся с помощью энергетических соотношений, полученных на основе общего выражения потенциальной энергии и равенства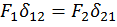 
, представляющего собой теорему о взаимности работ и перемещений (теорему Бетти). Работа первой силы 
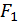на перемещении точки её приложения 
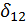под действием второй силы 
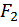равна работе второй силы 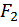на перемещении точки её приложения 
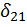под действием первой силы 
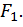В частном случае при 
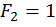можно записать 
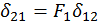. Но 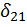– это перемещение сечения 2 под действием некоторой обобщенной силы .
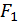Отсюда вытекает очень важный вывод, что если требуется определить перемещение в каком либо сечении, то в этом сечении по направлению перемещения необходимо приложить нагрузку, равную единице: 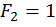. Выражая работу 
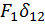через внутренние усилия в поперечном сечении стержня в единичном и грузовом состоянии, можно получить выражение для определения перемещения :
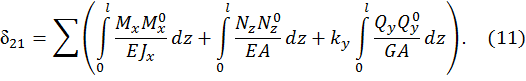
Данное выражение носит название формулы Максвелла – Мора (чаще используется одна фамилия Мора). В этой формуле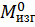 
, 
, 
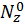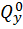– внутренние усилия, возникающие в поперечном сечении стержня, вызванные действием единичной силы 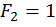или единичного момента 
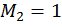, прикладываемых по направлению искомого перемещения. В первом случае перемещение 
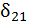является линейным, во втором – угловым.
Однако в большинстве случаев при изгибе влиянием продольных деформаций и деформаций сдвига от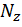 
и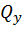 
соответственно можно пренебречь и учитывать лишь перемещения, вызванные изгибом. Тогда формула Мора для плоской системы может быть записана следующим образом:
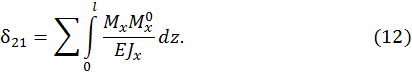
2.2. Порядок определения перемещений по методу Мора
1. Для каждого участка балки (плоской стержневой системы) составляется выражение изгибающего момента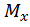 
в произвольном сечении от действия внешней нагрузки.
2. Строится вспомогательная балка (стержневая система) и нагружается единичной нагрузкой в точке, где требуется определить перемещение. При определении линейного перемещения в заданном направлении прикладывается единичная сила, при определении углового перемещения – единичный момент. Затем для каждого участка записывается выражение изгибающего момента 
от единичной нагрузки.
3. Записывается и вычисляется для каждого участка интеграл Мора. При этом если направление единичной нагрузки совпадает с направлением перемещения сечения, то получается положительный знак. Отрицательный знак свидетельствует, что направление перемещения сечения происходит в сторону, противоположную направлению единичной нагрузки.
2.3. Примеры определения перемещений по методу Мора
Пример 1. Определить способом Максвелла-Мора вертикальный прогиб и угол поворота сечения С (рис. 5) при известных F , a , E ,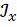 
.
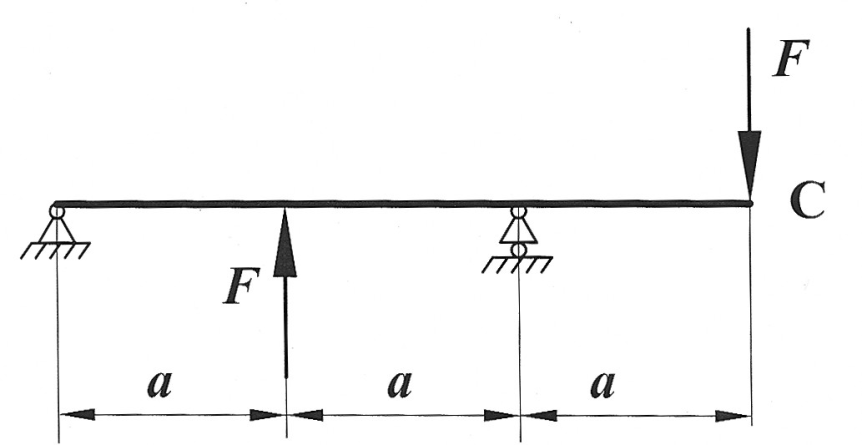
Рис. 5
Решение.
Перемещения сечений балки (прогиб и угол поворота) по методу Максвелла-Мора вычисляется по следующей формуле:
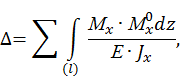
где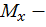 
изгибающий момент в текущем сечении балки от внешней нагрузки, 
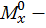изгибающий момент в том же сечении от единичной нагрузки.
Определим реакции опор RА и RВ, запишем выражения для определения изгибающего момента в сечении z на каждом участке от внешней нагрузки. Построим эпюры изгибающего момента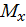 
от внешней нагрузки (грузовую эпюру, рис. 6, б):
= 
.
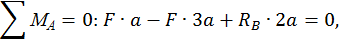
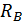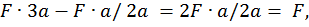
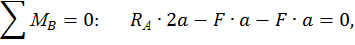
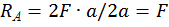Проверка:
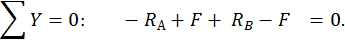
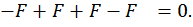
Строим эпюры :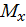
Первый участок: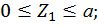 
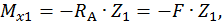
при 
:
,
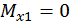при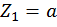 
:
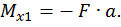
Второй участок: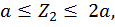 
,
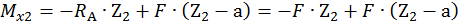при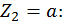 
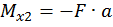
при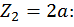 
.
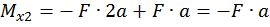Третий участок: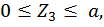 
,
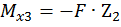при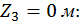 
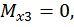
при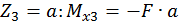 
.
При отыскании прогиба за единичную силу принимается груз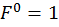 
, приложенный в том сечении, где отыскивается прогиб, то есть в сечении С (рис. 6, в).
Определим реакции опор RА и RВ, запишем выражения для определения изгибающего момента в сечении z на каждом участке от единичной силы 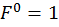. Построим эпюры изгибающего момента от единичной нагрузки (единичную эпюру, рис. 6, г):
= 
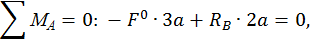
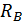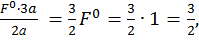
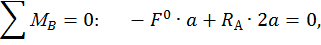
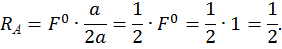
Проверка:
.
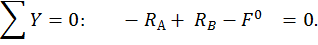
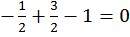Строим эпюры :
Первый участок: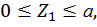 
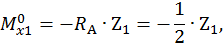
при :
,
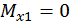при :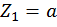
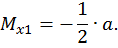
Второй участок: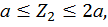 
,
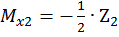при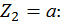 
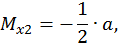
при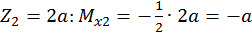 
.
Третий участок: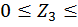 
а,
,
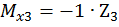при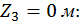
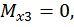
при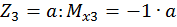 
.
По методу Максвелла-Мора вычисляем прогиб как сумму трех интегралов:
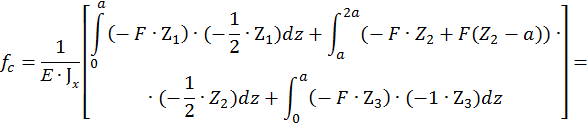
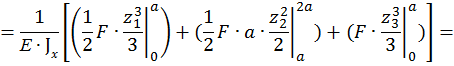
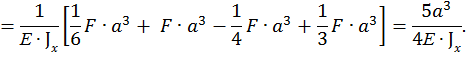
Знак «+» в ответе показывает, что прогиб направлен в ту же сторону, что и сила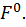 
При отыскании угла поворота в том сечении, где определяется угол поворота, то есть в сечении С, прикладывается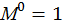 
(рис. 6, д).
Определим реакции опор RА и RВ, запишем выражения для определения изгибающего момента в сечении z на каждом участке от единичного момента 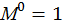. Построим эпюры изгибающего момента от единичного момента (рис. 6, е):
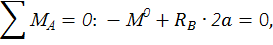
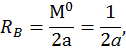
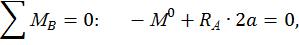
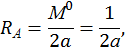
Проверка:
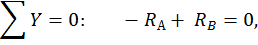
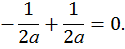
Строим эпюры :
Первый участок: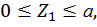
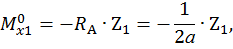
при :
,
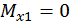при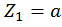 
:
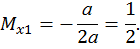
Второй участок: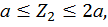
,
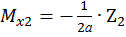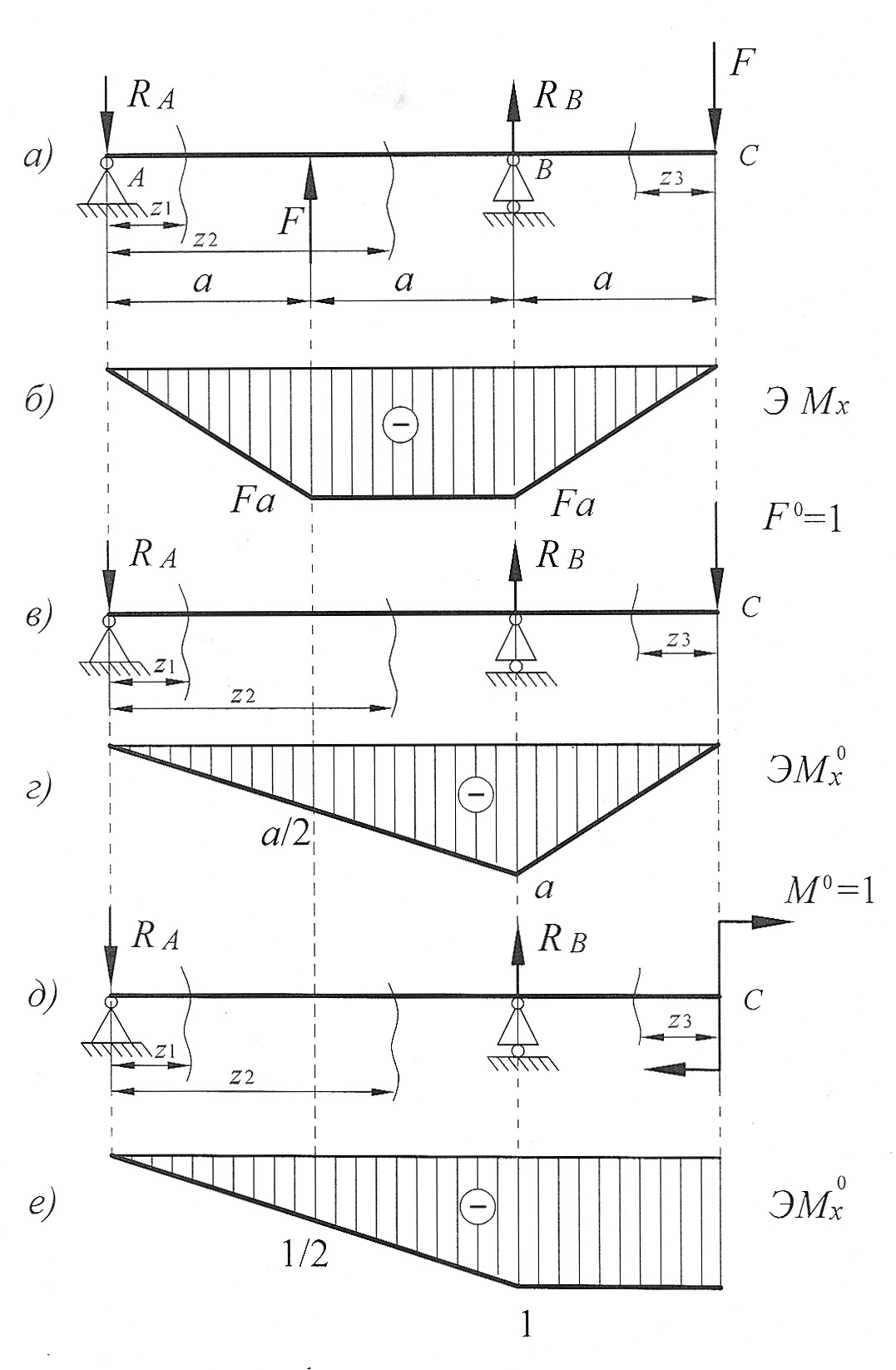
Рис. 6
при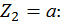
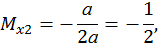
при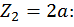
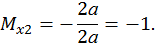
Третий участок: 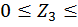а,
.
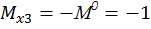По методу Максвелла-Мора вычисляем прогиб как сумму трех интегралов:
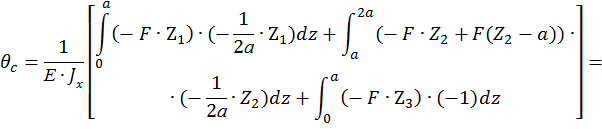
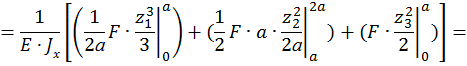
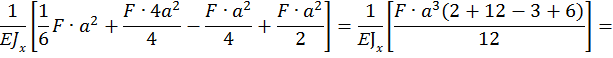
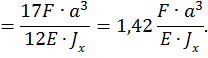
Знак «+» перед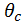 
показывает, что направление поворота сечения совпадает с направлением единичного момента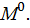 
ПРАВИЛО ВЕРЕЩАГИНА
Основные положения
К основным недостаткам определения перемещения при помощи интеграла Мора можно отнести необходимость составления аналитического выражения подынтегральной функции и её интегрирование. Это особенно неудобно при определении перемещений в стержне, имеющем большое количество участков. Однако, если стержень состоит из прямых участков с постоянной в пределах каждого участка жесткостью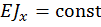 
, то операцию интегрирования можно упростить. Эти упрощения основываются на том, что эпюры изгибающего момента от единичной нагрузки на прямых участках оказываются всегда линейными. А.К. Верещагин предложил для стержней с постоянной жесткостью и с прямолинейной в пределах каждого участка осью вместо непосредственного вычисления интеграла Мора графоаналитический прием его определения.
Рассмотрим, например, две эпюры изгибающих моментов, из которых одна 
имеет произвольное очертание, а другая – прямолинейна (рис. 7).
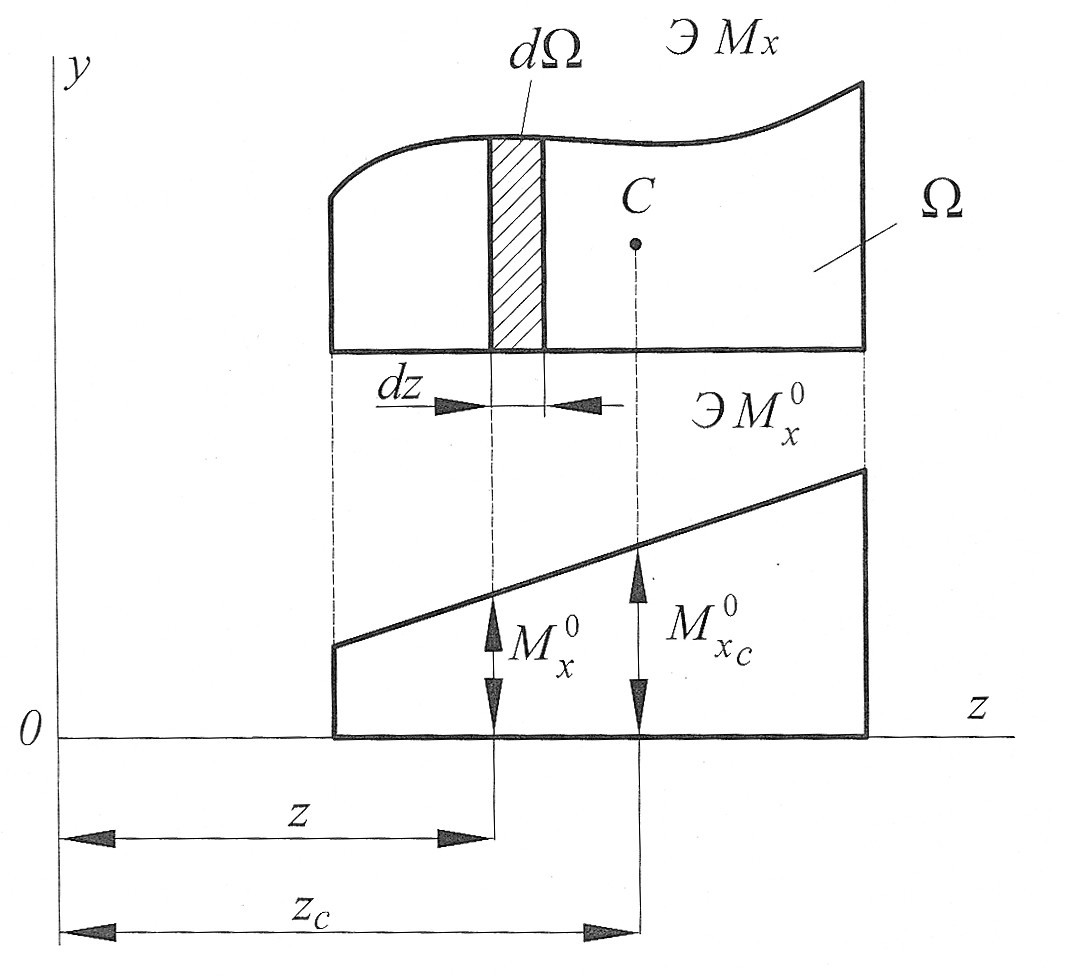
Рис. 7
В этом случае перемещение 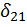по правилу А.К. Верещагина может быть вычислено как
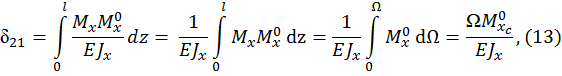
где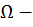 
площадь эпюры, построенной от внешней нагрузки,
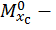ордината эпюры изгибающих моментов, построенной от единичной нагрузки и расположенной под центром тяжести эпюры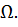 
Практически искомое перемещение 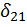может быть вычислено как произведение площади эпюры изгибающего момента от внешней нагрузки 
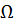на значение изгибающего момента 
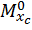от единичной нагрузки, расположенного под центром тяжести грузовой эпюры .
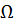Участки по изгибающему моменту следует различать не только по нагрузке, но и по жесткости поперечного сечения. Если эпюры и расположены по одну сторону от стержня, то произведение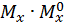 
положительно. Если обе эпюры прямолинейны, то безразлично, для какой из них находить площадь 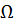или значение . Если эпюра имеет сложное очертание, то ее следует разбить на части, для которых просто определяется площадь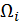 
и центр тяжести 
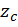. Чаще всего элементами разбиения площади эпюры 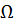являются: треугольник, прямоугольник и фигуры, очерченные квадратичными параболами (в случае действия равномерно распределенной нагрузки). Сведения о площадях и координатах центра тяжести простых эпюр (фигур) приведены в таблице 1.
Таблица 1. Значения площадей некоторых простейших эпюр
Дата: 2019-03-05, просмотров: 308.
