Упругой линии балки

Под действием внешних сил, вызывающих прямой поперечный изгиб, прямая ось балки искривляется, превращаясь в кривую линию, которая носит название упругой линии балки или изогнутой оси балки.

При деформации центр тяжести поперечного сечения получает линейное перемещение, перпендикулярное к недеформированной оси балки, которое называется прогибом и обозначается f ( y ). При этом поперечное сечение, оставаясь плоским, поворачивается вокруг нейтральной оси х на некоторый угол 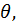 который называется углом поворота сечения (рис. 1).

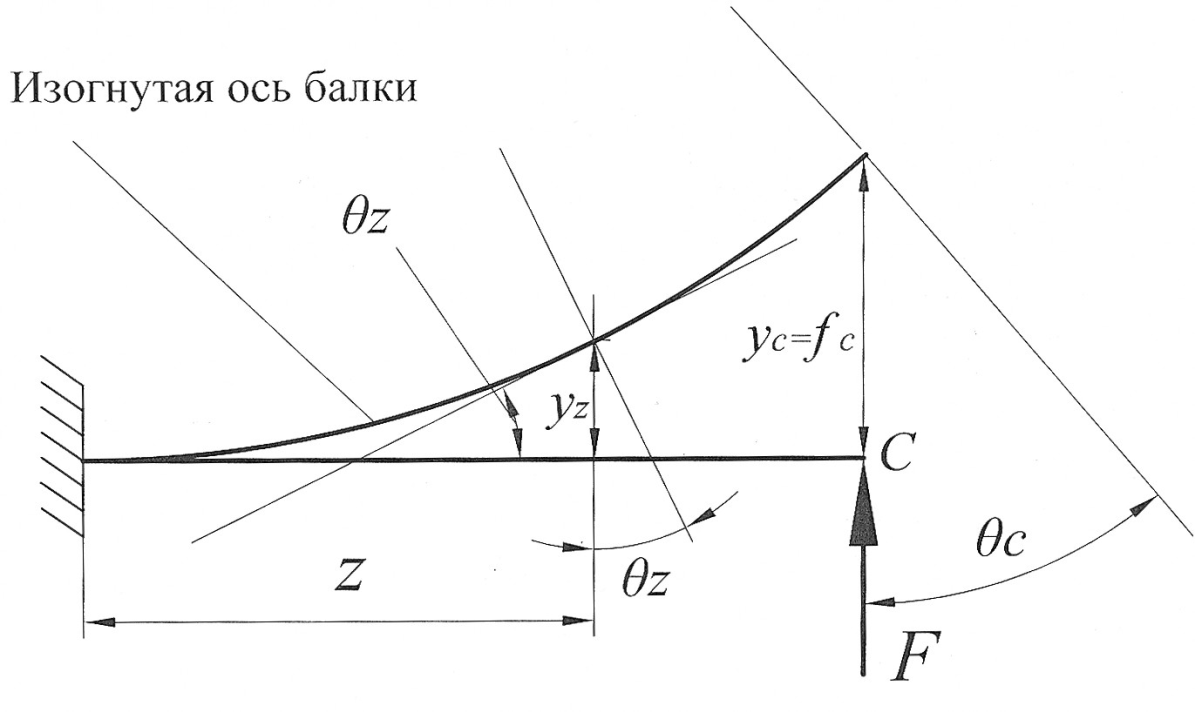
Рис. 1

Из аналитической геометрии известна прямая связь между тангенсом угла наклона касательной и первой производной от уравнения этой кривой. Следовательно,

Поскольку при малых углах поворота 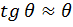, то выражение (1) может быть записано как

С одной стороны, кривизна изогнутой оси балки при чистом изгибе может быть определена из выражения

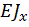Здесь  – изгибающиймомет,  – жесткость балки при изгибе.

С другой стороны, из математики известно соотношение между кривизной любой линии и её производными:

Для малых перемещений 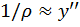. Тогда приближенное дифференциальное уравнение изогнутой оси балки примет вид

или

Интегрируя данное соотношение два раза, получаем уравнения для определения углов поворота и прогибов:

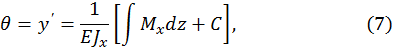
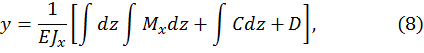
где C и D – постоянные интегрирования, которые определяются из условия деформации на опорах и на границах участков.

Определение перемещений методом непосредственного интегрирования приближенного дифференциального уравнения изогнутой оси для случая балок с большим количеством участков по изгибающему моменту сопряжено со значительными трудностями, поскольку приходится определять большое количество произвольных постоянных интегрирования. Если балка имеет несколько участков по изгибающему моменту, то для каждого участка приходится составлять свое уравнение , а после его интегрирования еще определять постоянные С и D, число которых равно удвоенному количеству участков. Задача становится весьма трудоемкой уже при трех участках.

Однако, используя специальные приемы, можно уменьшить число постоянных интегрирования до двух, то есть свести задачу к нахождению угла поворота 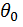и прогиба 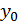в начале отсчета координат. Такой метод определения перемещения называется методом начальных параметров, а уравнение для определения прогибов в произвольном сечении называется универсальным уравнением упругой линии балки. Например, для балки (рис. 2) уравнения метода начальных параметров имеют вид

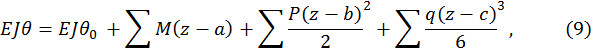
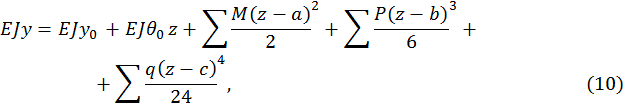
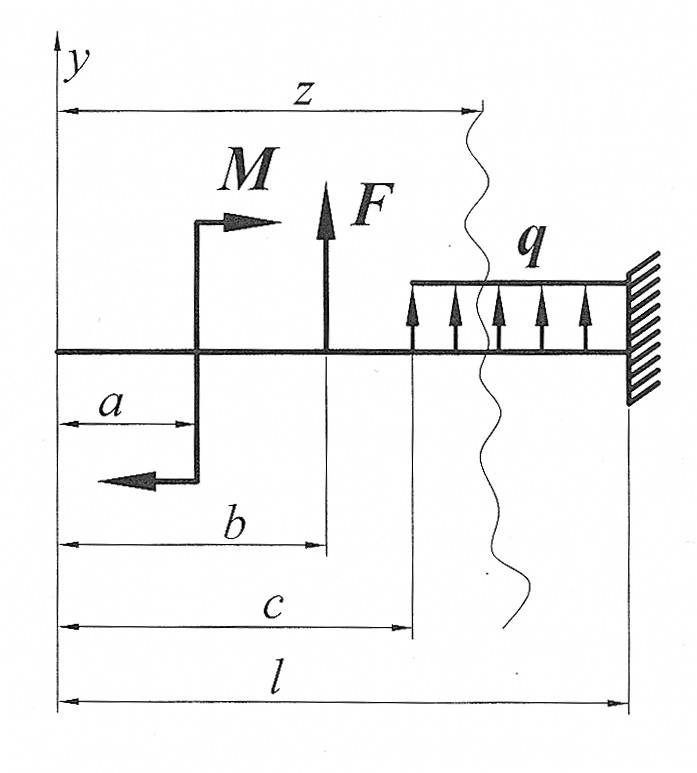
Рис. 2

В уравнения (9) и (10) включаются с соответствующими знаками все внешние нагрузки, расположенные между началом координат и сечением с абсциссой z на последнем правом участке. Внешние нагрузки, показанные на рисунке, включены в универсальные уравнения со знаком плюс, нагрузки противоположного направления включаются в уравнения со знаком минус. Важно отметить, что уравнения (9), (10) будут справедливы, если распределенная нагрузка q распространяется до сечения, где определяются перемещения. Если распределенная нагрузка q не доходит до данного сечения, её следует продолжить, одновременно добавив нагрузку, равную по величине, но противоположную по направлению. При вычислении перемещений в конкретном сечении учитываются только те нагрузки, которые расположены левее этого сечения.

Начальные параметры 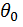 и 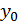 определяются из условий закрепления балки.

Недостаток универсальных уравнений состоит в том, что их нельзя непосредственно использовать для определения перемещений в балках, имеющих различную жесткость 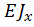 на разных участках. Кроме того, эти уравнения совсем неприменимы к балкам, имеющим непрерывно изменяющуюся по длине жесткость. В этих случаях следует применять общий метод определения перемещений – метод Мора.

1.2. Порядок определения перемещений методом                                       начальных параметров

1. Выбираем начало координат в крайнем левом сечении.

2. Определяем реакции опор.

3. Для произвольного сечения на последнем правом участке записываем оба уравнения для прогибов и углов поворота.

4. Находим начальные параметры (прогиб 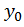 и угол поворота  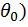в начале отсчета. Если в начале отсчета расположена жесткая заделка, то начальные параметры будут равны нулю (  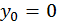и 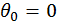). Если в начале отсчета окажется шарнирная опора, то прогиб в начале отсчета будет равен нулю ( 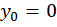). В общем случае записываем выражения для определения прогибов в сечениях с шарнирными опорами и, приравняв их нулю, находим  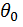и .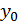

6. Вычисляем перемещения в заданных сечениях, подставляя в уравнения (пункт 3) конкретные значения координат этих сечений и учитывая только те нагрузки, которые расположены левее соответствующих сечений.

1.3. Примеры определения перемещений при изгибе