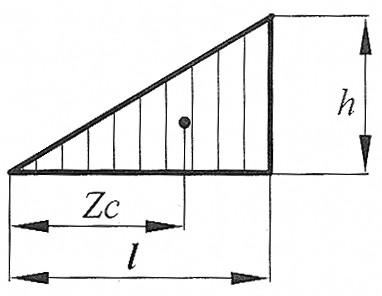
| Вид эпюры | Площадь эпюры 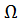
| Расстояние до центра тяжести 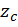
|
|
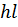
|
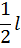
|
|
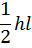
|
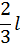
|
|
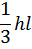
|
|
|
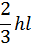
|
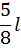
|
3.2. Порядок определения перемещений по способу Верещагина
1. Строим грузовую эпюру изгибающих моментов (от внешней нагрузки).
2. Строим две единичные эпюры. Для определения прогиба y строим единичную эпюру от силы 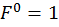 , приложенной в том сечении, где нужно найти прогиб. Для определения угла поворота
, приложенной в том сечении, где нужно найти прогиб. Для определения угла поворота 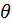 строим единичную эпюру от момента
строим единичную эпюру от момента 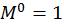 , приложенного в том сечении, где нужно найти угол поворота.
, приложенного в том сечении, где нужно найти угол поворота.
3. Далее перемножаем площадь грузовой эпюры 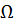 на значение момента, взятого у единичной эпюры под центром тяжести грузовой эпюры
на значение момента, взятого у единичной эпюры под центром тяжести грузовой эпюры 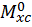 , и делим на жесткость балки
, и делим на жесткость балки 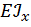 . Если у балки несколько участков, то
. Если у балки несколько участков, то 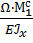 вычисляем по каждому участку и далее суммируем.
вычисляем по каждому участку и далее суммируем.
4. Если эпюры грузовая и единичная построены в одну сторону от оси z, то прогиб и угол поворота имеют знак «+», и наоборот – «-». Если прогиб и угол поворота получились со знаком «-», это означает, что их направление противоположно направлению единичной силы или единичного момента.
Примеры разбиения сложных площадей эпюр
Изгибающих моментов
Пример 1. Предположим, что эпюры изгибающих моментов, построенные от внешней нагрузки, представляют собой однозначную трапецию (рис. 8).
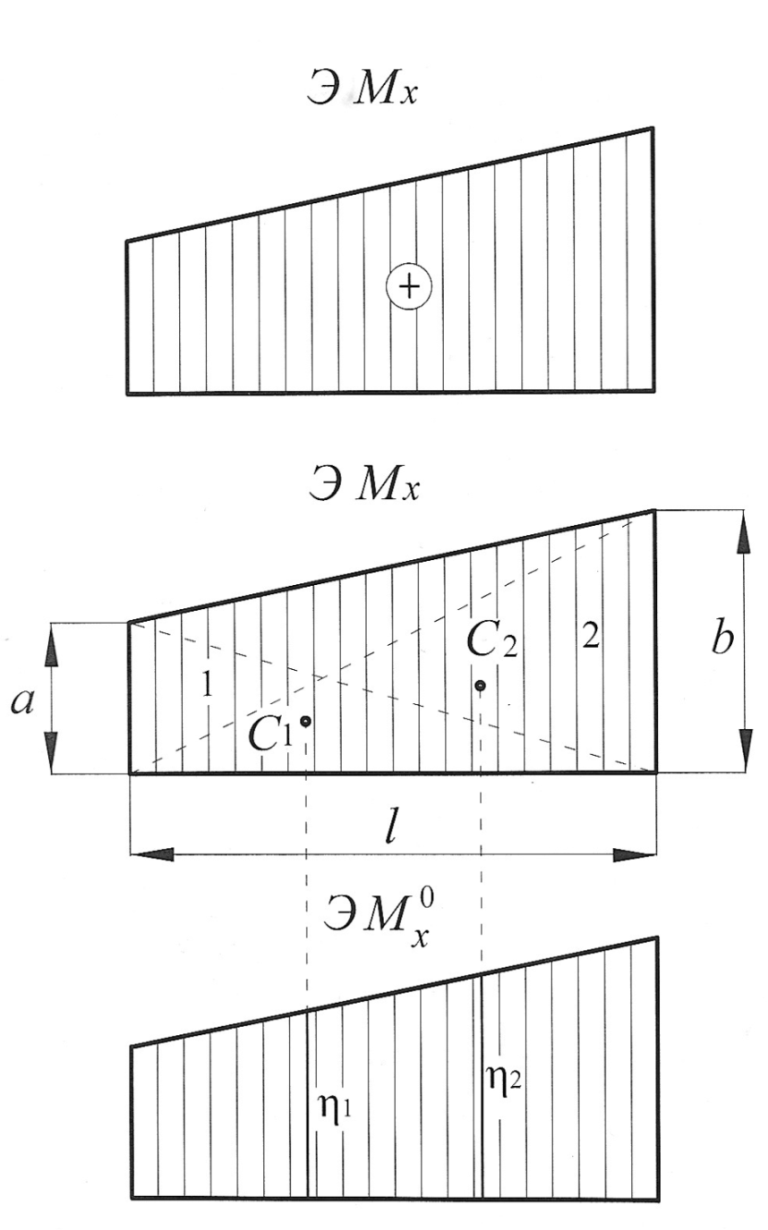
Рис. 8
Разбиваем эпюру  на два однозначных треугольника с площадями
на два однозначных треугольника с площадями 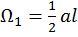 ,
, 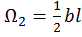 . Обозначим значения единичных моментов под центрами тяжести треугольников как
. Обозначим значения единичных моментов под центрами тяжести треугольников как 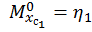 и
и 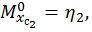 тогда
тогда
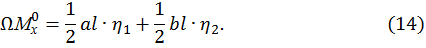
Пример 2. Эпюра от внешней нагрузки представляет собой разнозначную трапецию (рис. 9).
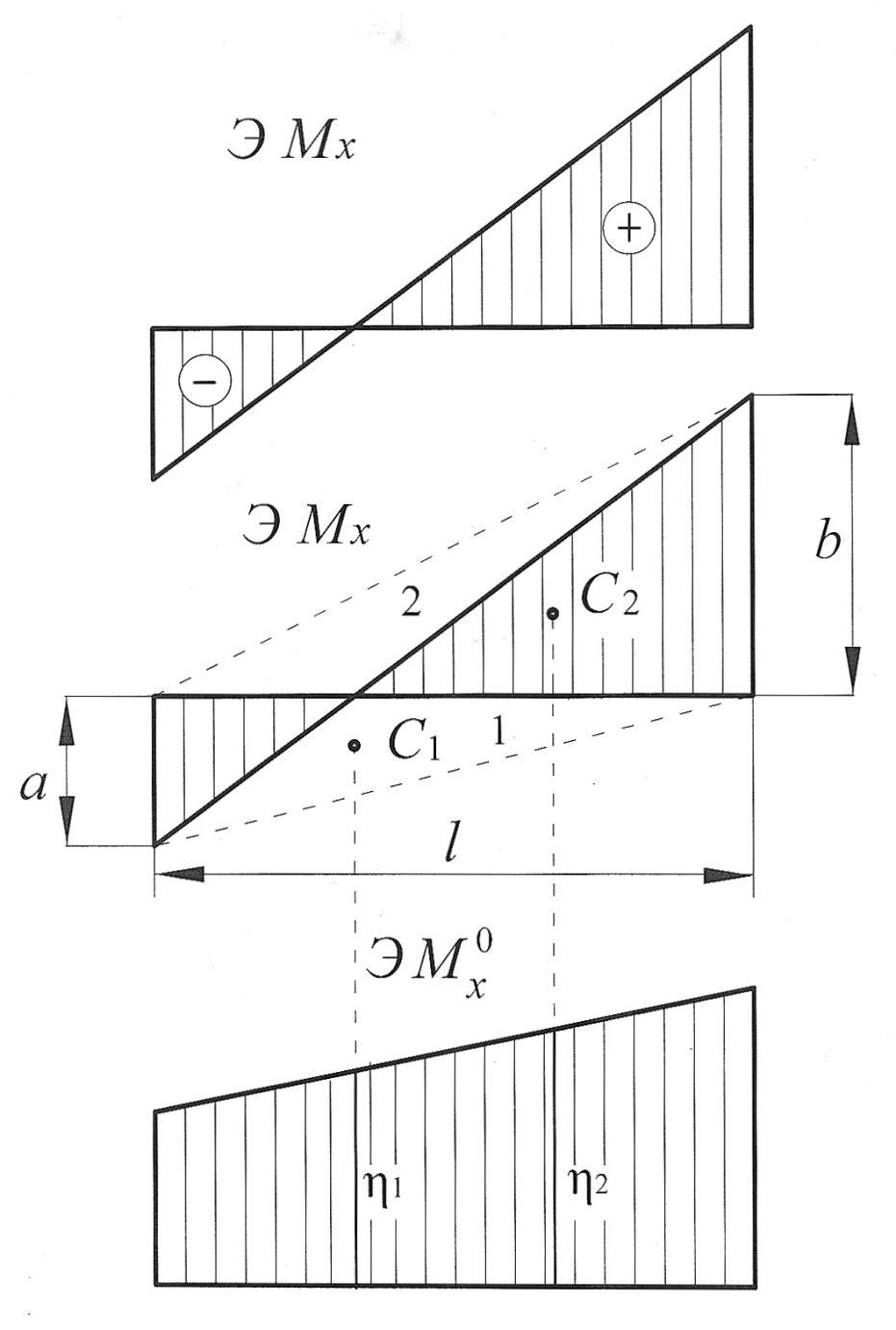
Рис. 9
Разбиваем эпюру 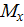 на два разнозначных треугольника. Один треугольник (1) расположен снизу от оси z, второй треугольник (2) расположен сверху от оси z. Произведение
на два разнозначных треугольника. Один треугольник (1) расположен снизу от оси z, второй треугольник (2) расположен сверху от оси z. Произведение 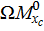 имеет знак минус, если эпюры
имеет знак минус, если эпюры 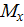 и
и 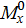 расположены по разные стороны от оси z, и наоборот,
расположены по разные стороны от оси z, и наоборот, 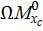 имеет знак плюс, если эпюры
имеет знак плюс, если эпюры 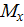 и
и 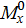 расположены по одну сторону от оси z , тогда
расположены по одну сторону от оси z , тогда
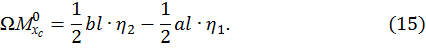
Пример 3. Эпюра  от внешней нагрузки (грузовая эпюра) представляет собой однозначную трапецию, ограниченную сверху параболой (рис. 10).
от внешней нагрузки (грузовая эпюра) представляет собой однозначную трапецию, ограниченную сверху параболой (рис. 10).
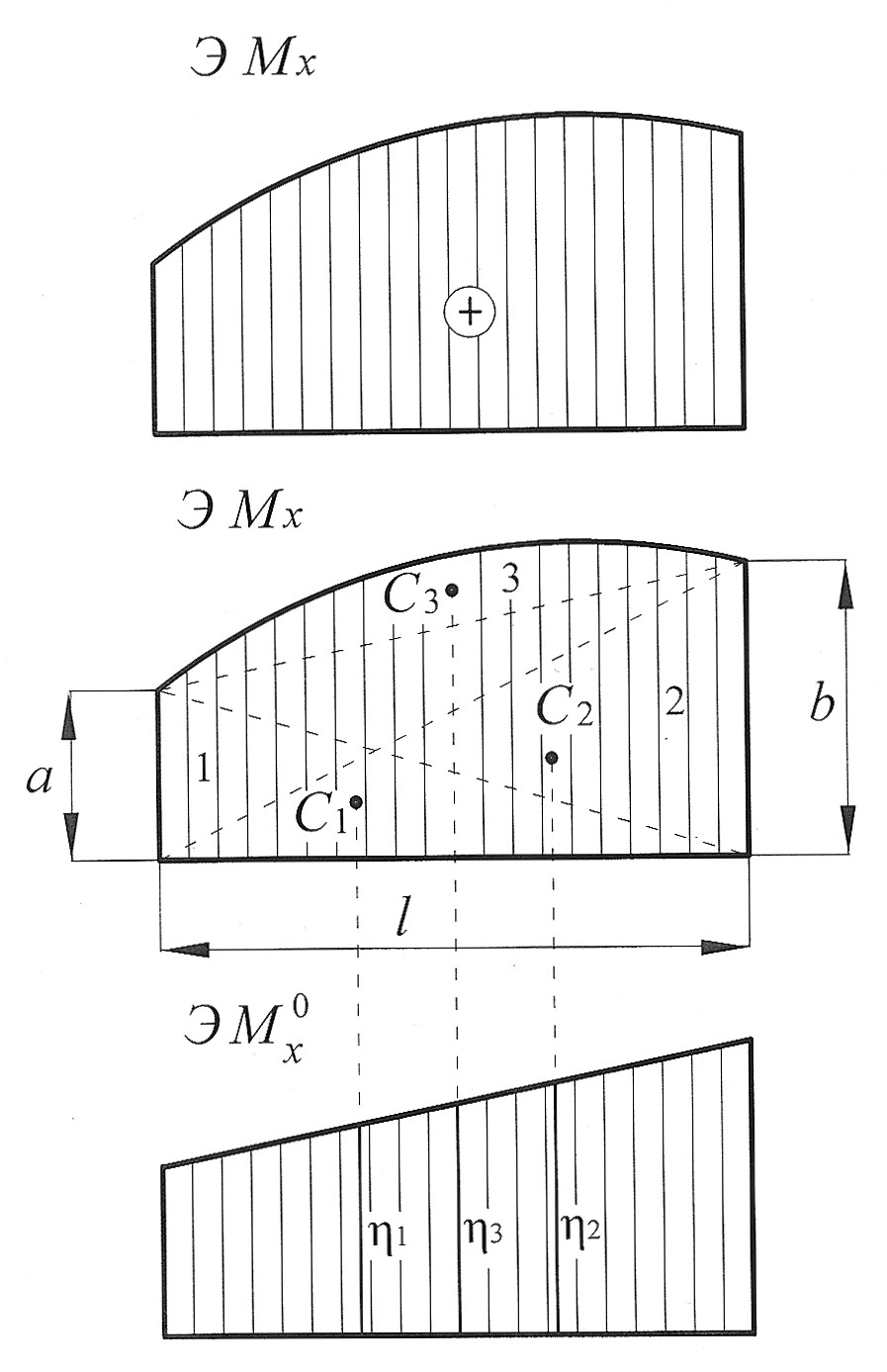
Рис. 10
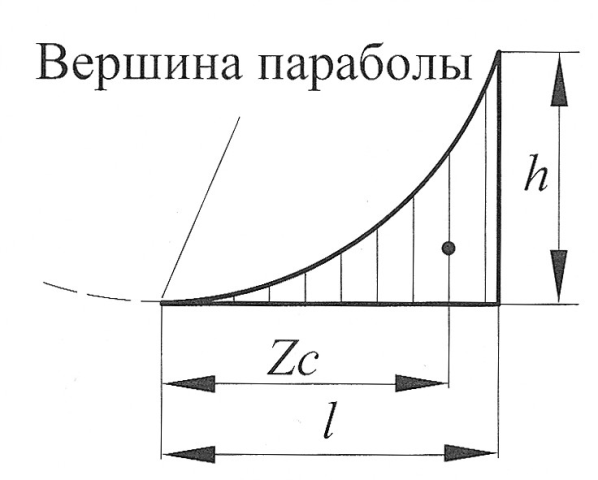
Разбиваем эпюру  на два однозначных треугольника и квадратичную параболу с нулевыми начальным и конечным значениями c площадью
на два однозначных треугольника и квадратичную параболу с нулевыми начальным и конечным значениями c площадью 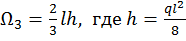 , и с центром тяжести
, и с центром тяжести 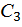 , который находится на середине длины l, тогда
, который находится на середине длины l, тогда
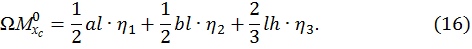
Пример 4. Эпюра 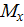 от внешней нагрузки (грузовая эпюра) представляет собой разнозначную трапецию, ограниченную сверху параболой (рис. 11).
от внешней нагрузки (грузовая эпюра) представляет собой разнозначную трапецию, ограниченную сверху параболой (рис. 11).
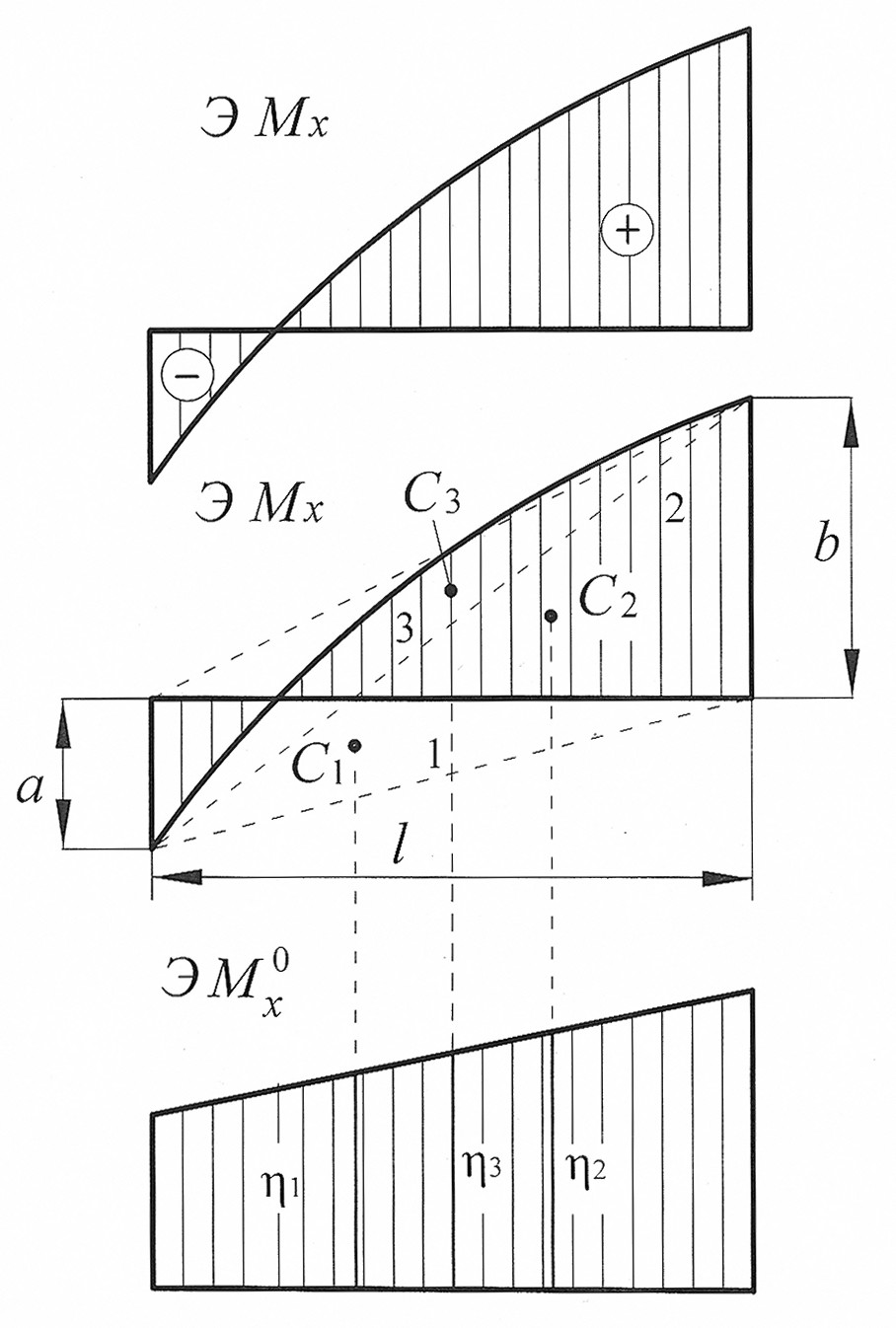
Рис. 11
Разбиваем эпюру 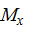 на два разнозначных треугольника и квадратичную параболу с нулевыми начальным и конечным значениями с площадью
на два разнозначных треугольника и квадратичную параболу с нулевыми начальным и конечным значениями с площадью 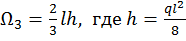 , и с центром тяжести
, и с центром тяжести 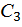 , который находится на середине длины l, тогда
, который находится на середине длины l, тогда
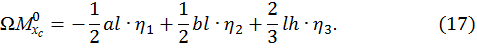
Пример 5. Предположим, эпюра  , построенная от внешней нагрузки (грузовая эпюра), представляет собой треугольник, ограниченный сверху выпуклой параболой. Такая эпюра получается, например, если консольная балка нагружена на свободном конце сосредоточенной силой, направленной вверх, и распределенной нагрузкой, направленной вниз (рис. 12).
, построенная от внешней нагрузки (грузовая эпюра), представляет собой треугольник, ограниченный сверху выпуклой параболой. Такая эпюра получается, например, если консольная балка нагружена на свободном конце сосредоточенной силой, направленной вверх, и распределенной нагрузкой, направленной вниз (рис. 12).
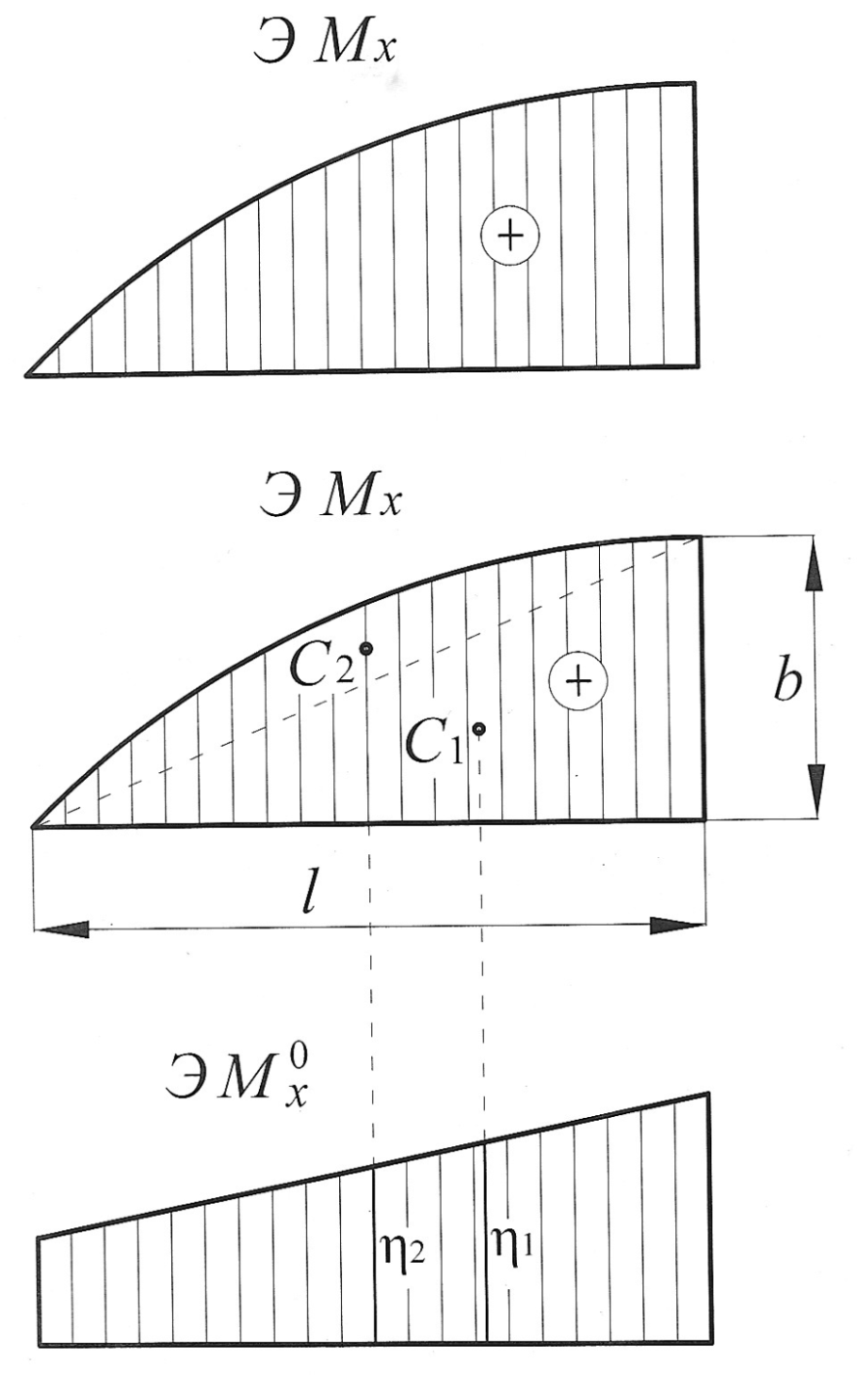
Рис. 12
Разбиваем эпюру  на треугольник с площадью
на треугольник с площадью 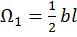 и центром тяжести
и центром тяжести 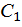 и квадратичную параболу с нулевыми начальным и конечным значениями с площадью
и квадратичную параболу с нулевыми начальным и конечным значениями с площадью 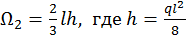 , и центром тяжести
, и центром тяжести 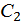 , тогда
, тогда
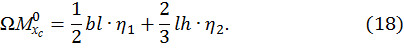
Пример 6. Предположим, эпюра 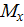 , построенная от внешней нагрузки (грузовая эпюра), представляет собой треугольник, ограниченный сверху вогнутой параболой. Такая эпюра получается, например, если консольная балка нагружена на свободном конце сосредоточенной силой и распределенной нагрузкой, которые направлены вверх (рис. 13).
, построенная от внешней нагрузки (грузовая эпюра), представляет собой треугольник, ограниченный сверху вогнутой параболой. Такая эпюра получается, например, если консольная балка нагружена на свободном конце сосредоточенной силой и распределенной нагрузкой, которые направлены вверх (рис. 13).
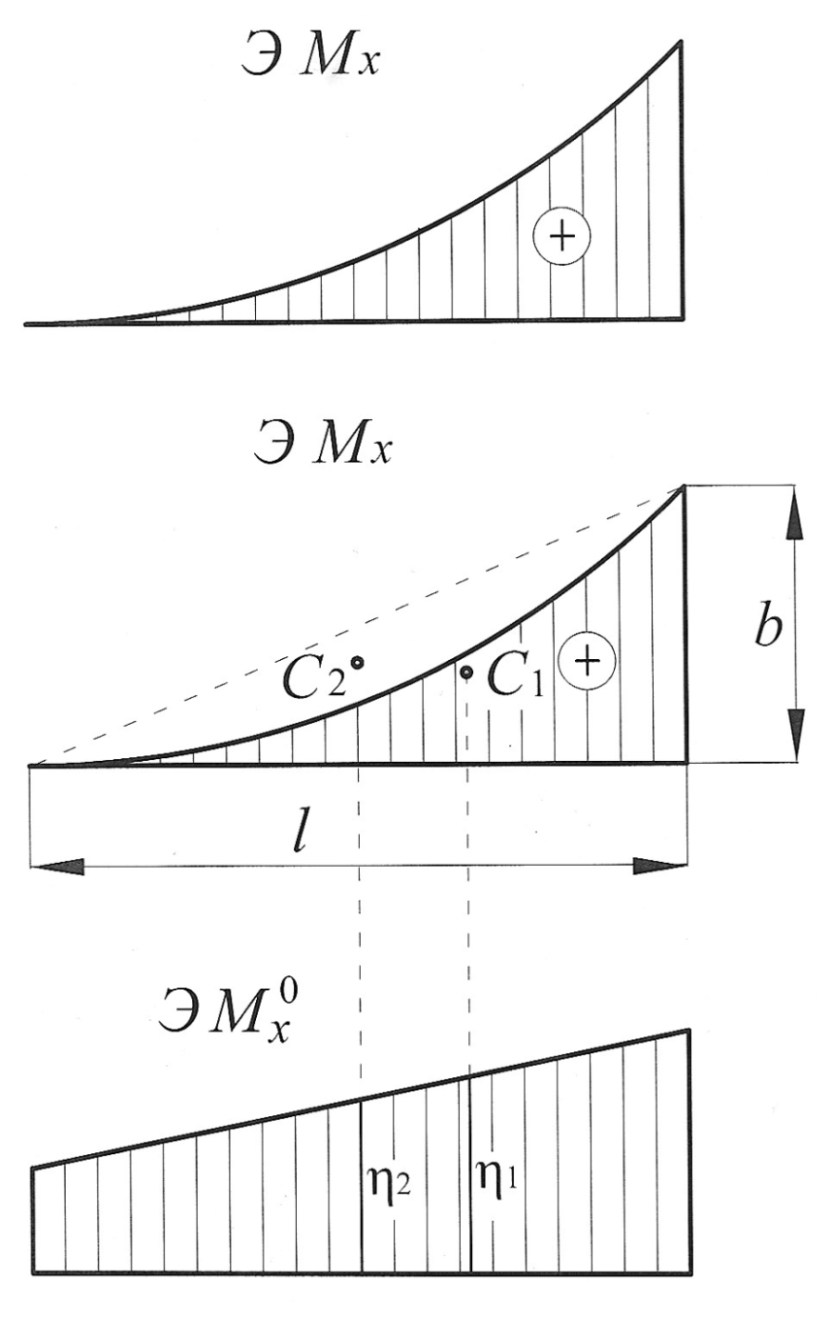
Рис. 13
Разбиваем эпюру 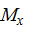 на треугольник с площадью
на треугольник с площадью 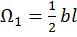 и с центром тяжести
и с центром тяжести 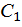 и квадратичную параболу с нулевыми начальным и конечным значениями с площадью
и квадратичную параболу с нулевыми начальным и конечным значениями с площадью 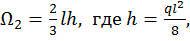 и центром тяжести
и центром тяжести 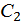 , тогда
, тогда
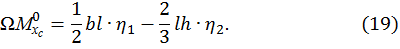
3.4. Пример определения перемещений по способу Верещагина
Пример 1. Определить способом Верещагина величину вертикального перемещения и угол поворота свободного конца консольной двутавровой балки № 24 (рис. 14).
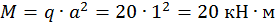 ,
, 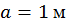 ,
, 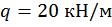 ,
,
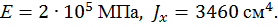
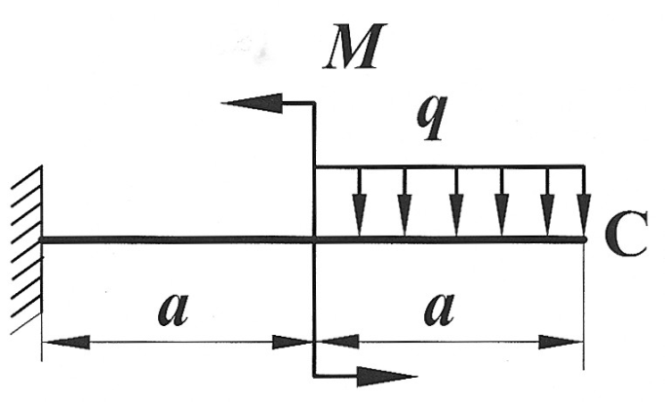
Рис. 14
Решение.
Любые перемещения  при нескольких прямолинейных участках нагружения балки вычисляются по правилу Верещагина по следующей формуле:
при нескольких прямолинейных участках нагружения балки вычисляются по правилу Верещагина по следующей формуле:
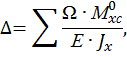
где 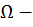 площадь эпюры изгибающего момента от заданной нагрузки,
площадь эпюры изгибающего момента от заданной нагрузки,
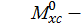 ордината эпюры изгибающего момента от единичной нагрузки.
ордината эпюры изгибающего момента от единичной нагрузки.
Ордината 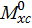 берется в том сечении участка балки, напротив которого находится центр тяжести эпюры изгибающего момента от заданной нагрузки на этом участке.
берется в том сечении участка балки, напротив которого находится центр тяжести эпюры изгибающего момента от заданной нагрузки на этом участке.
Построим эпюры изгибающего момента 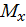 от внешней нагрузки (рис. 15, б):
от внешней нагрузки (рис. 15, б):
Первый участок: 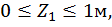
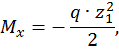
при  :
:
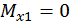 ,
,
при 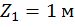 :
:
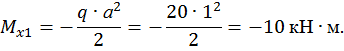
Второй участок: 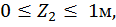
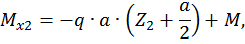
при 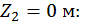
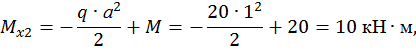
при 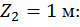
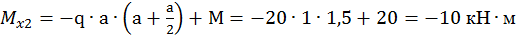 .
.
Для определения вертикального перемещения свободного конца консольной балки необходимо в этом сечении приложить силу 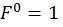 (рис. 15, в) и построить от этой силы единичную эпюру изгибающего момента
(рис. 15, в) и построить от этой силы единичную эпюру изгибающего момента 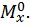
Построим эпюры изгибающего момента  (единичную эпюру рис. 15, г):
(единичную эпюру рис. 15, г):
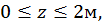
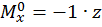 ,
,
при 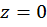 :
:
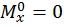 ,
,
при 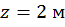 :
:
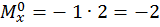 .
.
Эпюру изгибающего момента от заданной внешней нагрузки (грузовую эпюру) разбиваем на простые фигуры, образованные квадратичной параболой и двумя треугольниками, один сверху, а второй снизу от оси z (см. рис. 15, б).
Определим площади этих фигур 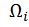 и
и 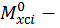 ординаты эпюры изгибающего момента от единичной нагрузки под центром тяжести эпюры изгибающего момента от заданной нагрузки на каждом участке (см. рис. 15, б, г):
ординаты эпюры изгибающего момента от единичной нагрузки под центром тяжести эпюры изгибающего момента от заданной нагрузки на каждом участке (см. рис. 15, б, г):
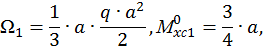
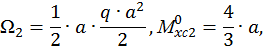
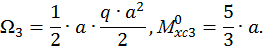
Если эпюры грузовая и единичная построены по одну сторону от оси z, то произведение 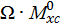 имеет знак «+», и наоборот – «-». Отсюда следует, что на втором участке
имеет знак «+», и наоборот – «-». Отсюда следует, что на втором участке 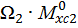 имеет знак «-».
имеет знак «-».
Определяем прогиб свободного конца балки:
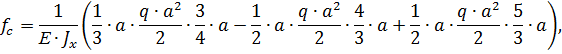
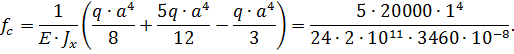
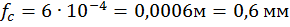 .
.
Прогиб 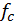 получился со знаком «+», это значит, что его направление соответствует направлению единичной силы.
получился со знаком «+», это значит, что его направление соответствует направлению единичной силы.
Для определения вертикального угла поворота свободного конца консольной балки необходимо в этом сечении приложить момент 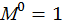 (рис. 15, д) и построить от этого момента единичную эпюру изгибающего момента
(рис. 15, д) и построить от этого момента единичную эпюру изгибающего момента 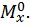
Построим от 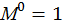 эпюры изгибающего момента
эпюры изгибающего момента  (единичную эпюру, рис. 15, е):
(единичную эпюру, рис. 15, е):
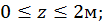
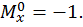
Так как площади грузовой эпюры на каждом участке уже найдены, то определим 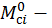 ординаты эпюры изгибающего момента от единичной нагрузки (единичного момента) под центром тяжести эпюры изгибающего момента от заданной нагрузки на каждом участке:
ординаты эпюры изгибающего момента от единичной нагрузки (единичного момента) под центром тяжести эпюры изгибающего момента от заданной нагрузки на каждом участке:
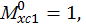
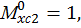
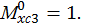
Определяем угол поворота балки со свободного конца:
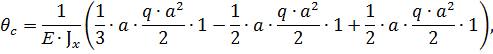
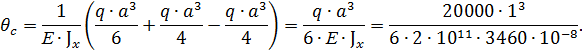
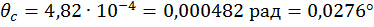
Значение угла поворота балки получилось со знаком «+», это значит, что балка поворачивается в том же направлении как действует единичный момент.
Ответ: 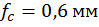 ,
, 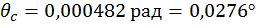 .
.
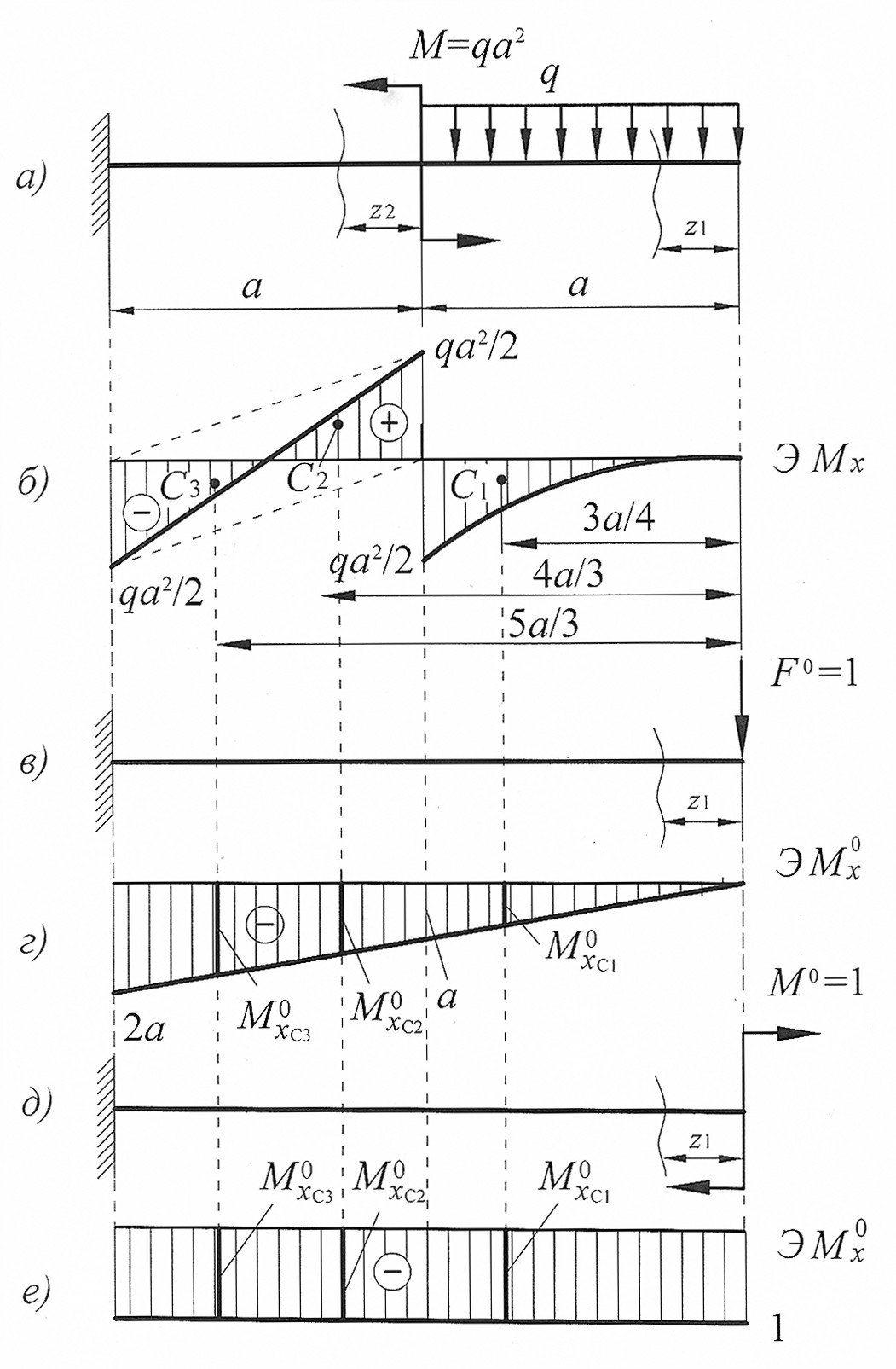
Рис. 15
ЗАДАЧИ ДЛЯ ПРОВЕРКИ СТУДЕНТАМИ СТЕПЕНИ УСВОЕНИЯ МАТЕРИАЛА РАЗДЕЛА «ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ПРИ ИЗГИБЕ»
Задача 1
По методу начальных параметров определить прогиб в сечении С и угол поворота в опоре А, если:
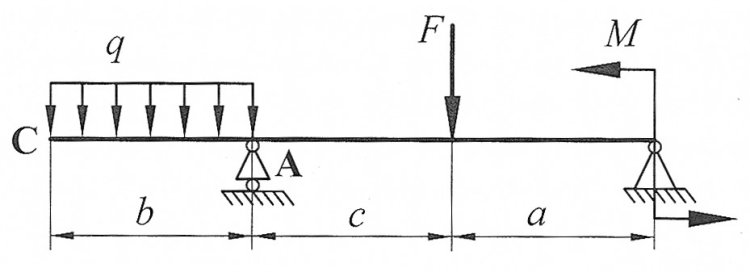
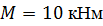 , , 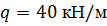 , ,
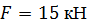 , , 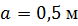 , ,
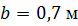 , , 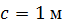 , ,
 , ,
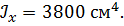
|
|
Задача 2
По методу начальных параметров определить прогиб в сечении С и угол поворота в опоре А, если:
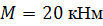 , , 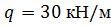 , ,
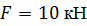 , , 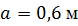 , ,
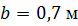 , , 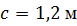 , ,
 , ,
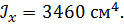
|
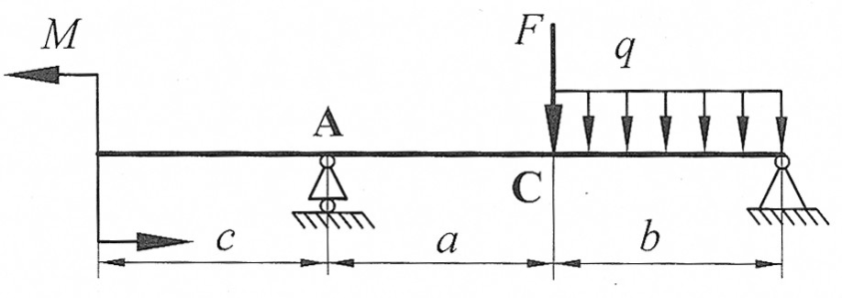
|
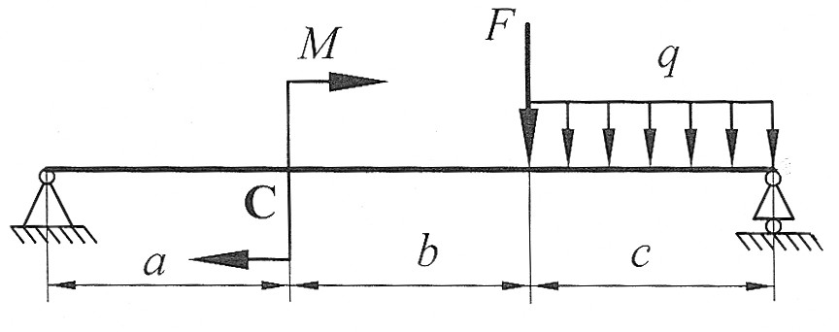
Задача 3
По методу начальных параметров определить прогиб и угол поворота в сечении С, если:
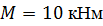 , , 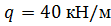 , ,
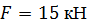 , , 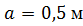 , ,
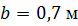 , , 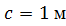 , ,
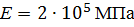 , ,
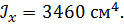
|
|
Задача 4
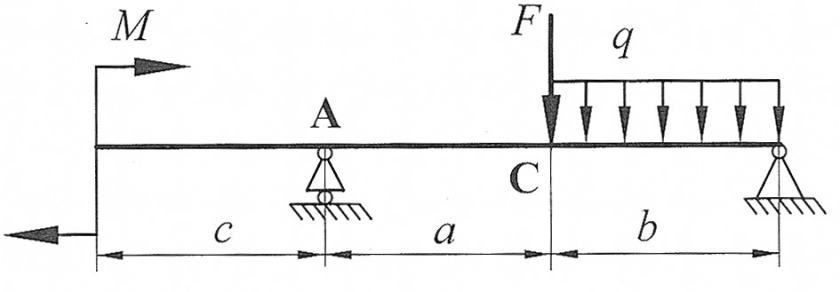
| По методу начальных параметров определить прогиб в сечении С и угол поворота в опоре А, если:
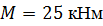 , ,
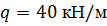 , ,
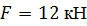 , , 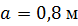 , ,
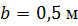 , , 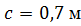 , ,
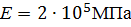 , , 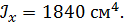
|
Задача 5
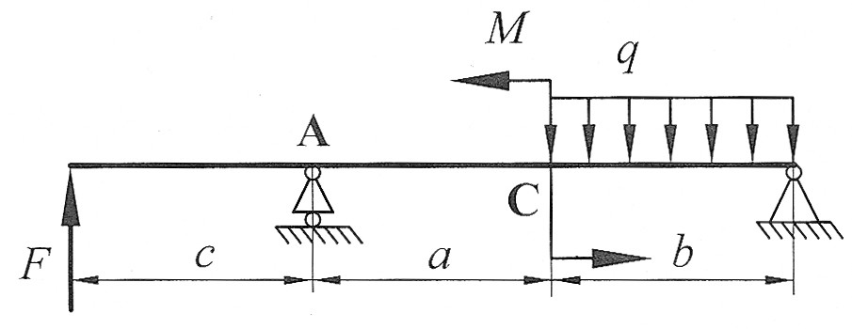
| По методу начальных параметров определить прогиб в сечении С и угол поворота в опоре А, если:
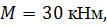
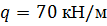 , ,
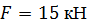 , , 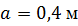 , ,
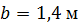 , , 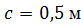 , ,
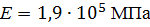 , , 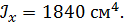
|
Задача 6
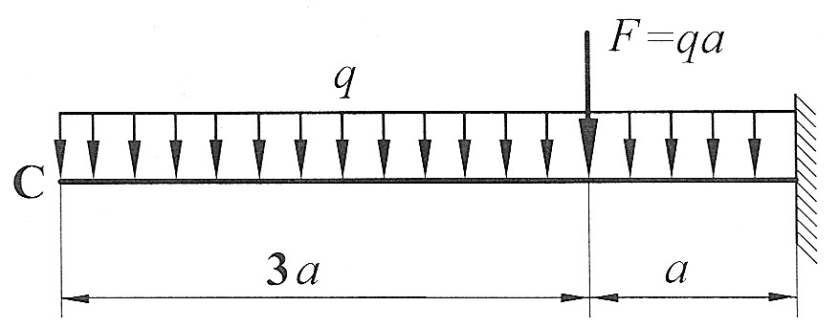
| По методу начальных параметров определить прогиб и угол поворота в сечении С, если:
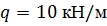 , ,
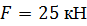 , , 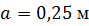 , ,
 , ,
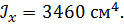
|
Задача 7
Определить способом Верещагина величину вертикального перемещения и угол поворота свободного конца консольной балки (сечения С).
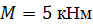 , ,
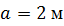 , ,
 , ,
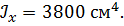
|

|
Задача 8
Определить способом Мора величину вертикального перемещения и угол поворота сечения С балки.
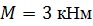 , ,
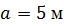 , ,

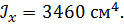
|
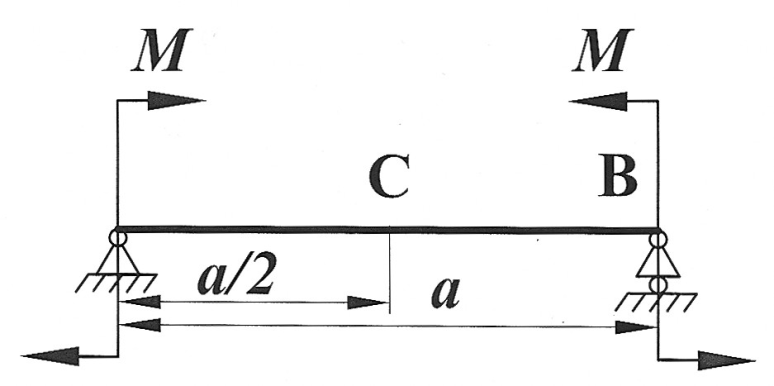
|
Задача 9
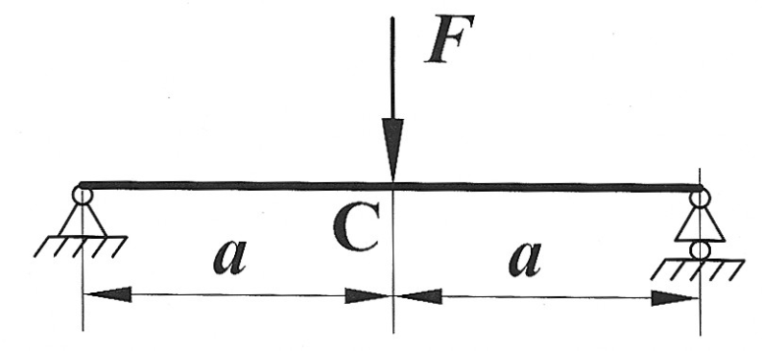
Определить способом Мора величину вертикального перемещения и угол поворота по середине пролета балки (сечения С).
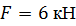 , ,
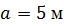 , ,
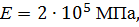
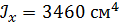 . .
|
|
Задача 10
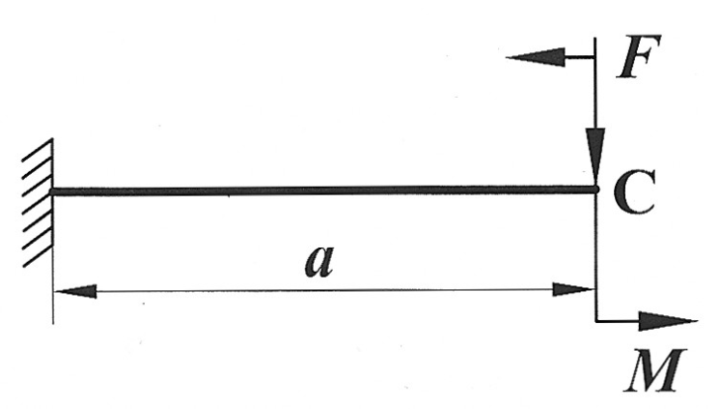
| Определить способом Мора величину вертикального перемещения и угол поворота свободного конца консольной балки (сечения С).
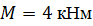 , ,
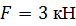
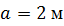 , ,
 , , 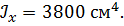
|
Задача 11
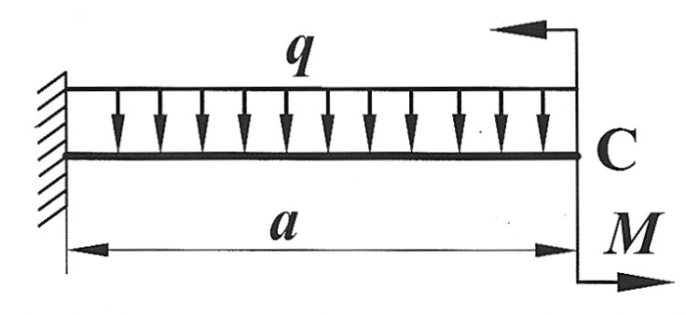
| Определить способом Мора величину вертикального перемещения и угол поворота свободного конца консольной балки (сечения С).
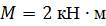 , ,
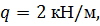
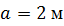 , ,
 , , 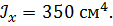
|
Задача 12
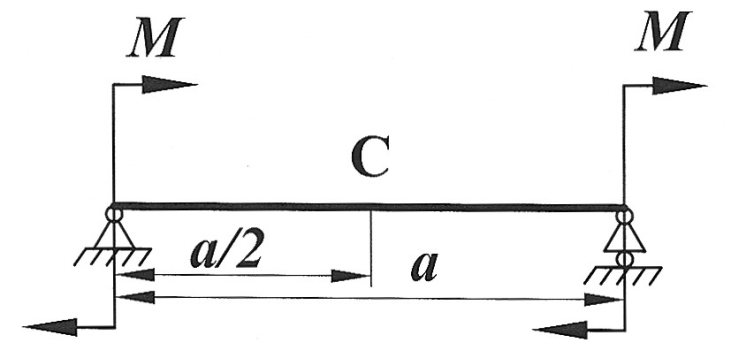
| Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С балки.
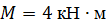 , ,
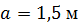 , ,
 , ,
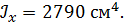
|
Задача 13
Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С стальной двутавровой балки № 27.
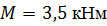 , ,
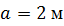 , ,
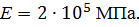
|
|
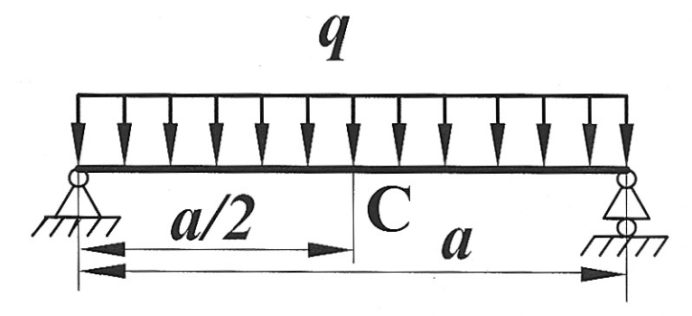
Задача 14
Определить способом Мора величину вертикального перемещения и угол поворота сечения С балки.
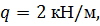
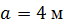 , ,
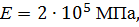
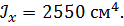
|
|
Задача 15
Определить способом Мора величину вертикального перемещения и угол поворота сечения С стальной двутавровой балки № 20.
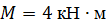 , ,
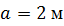 , ,
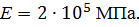
|
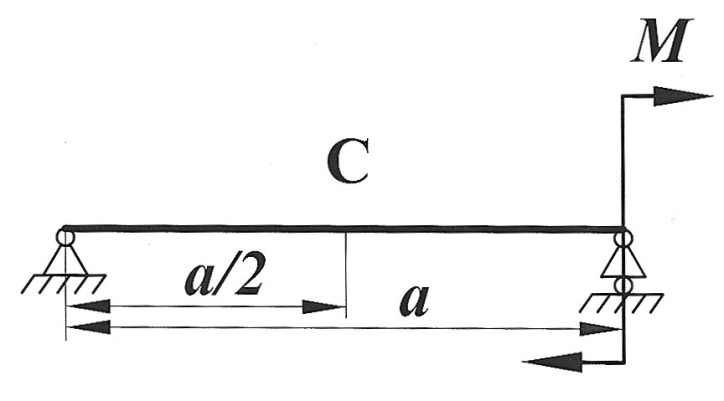
|
Задача 16
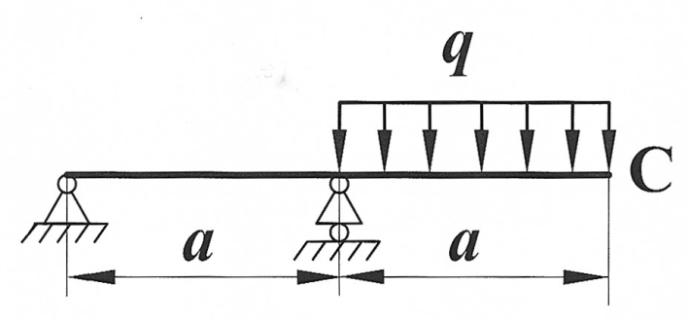
| Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С балки.
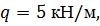
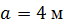 , ,
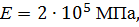
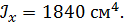
|
Задача 17
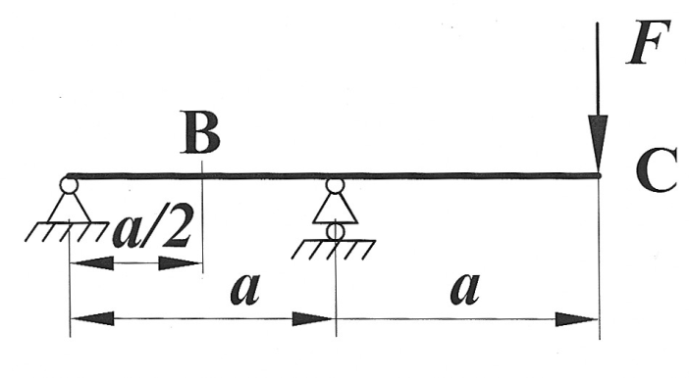
| Определить способом Верещагина величину вертикального перемещения сечения В и угол поворота сечения С балки.
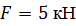 , ,
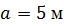 , ,
 , ,
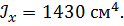
|
Задача 18
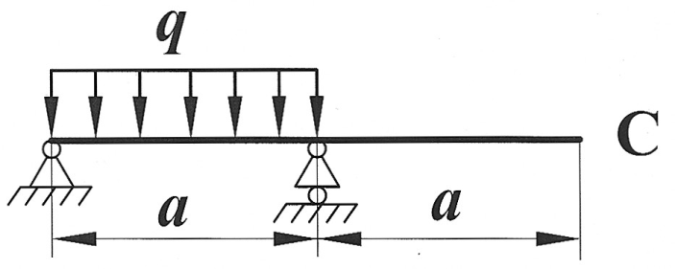
|
Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С стальной двутавровой балки
№ 20.
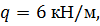
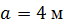 , ,
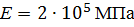
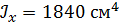 . .
|
Задача 19
Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С балки.
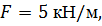
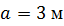 , ,
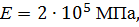
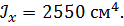
|
|
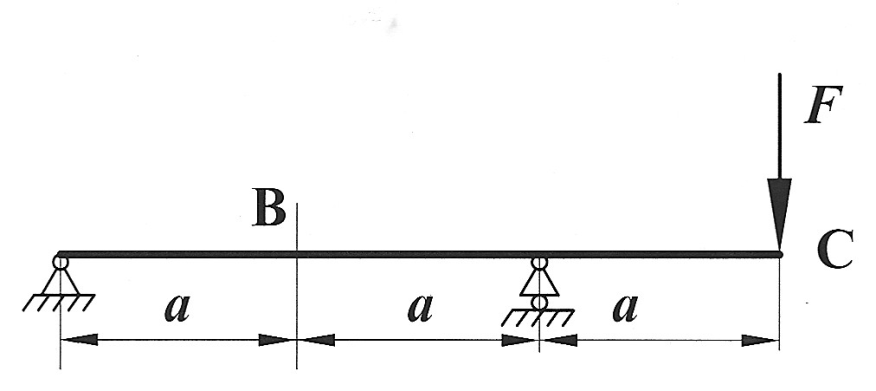
Задача 20
Определить способом Верещагина величину вертикального перемещения сечения В и угол поворота сечения С балки.
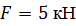 , ,
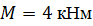 , ,

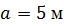 , ,
 , ,
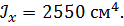
|
|
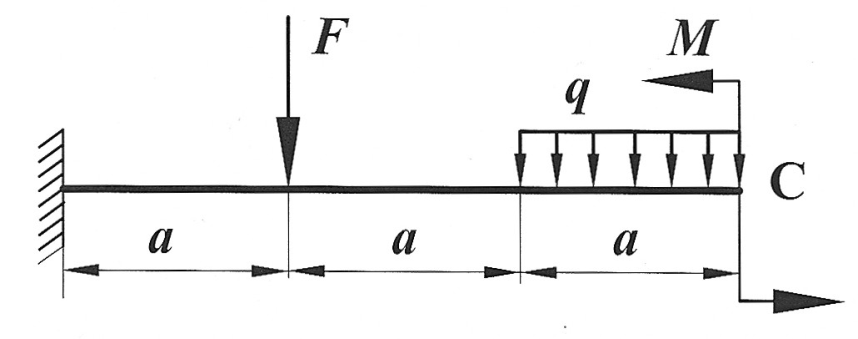
Задача 21
Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С стальной двутавровой балки № 20.
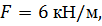
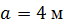 , ,
 , , 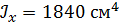 . .
|
|
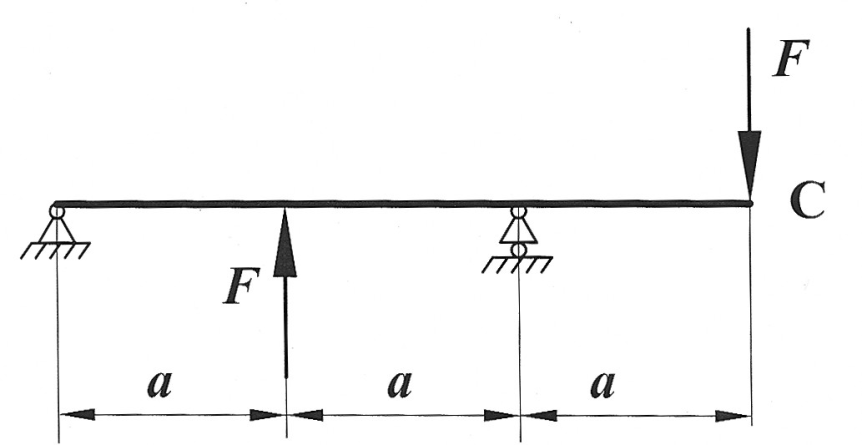
Задача 22
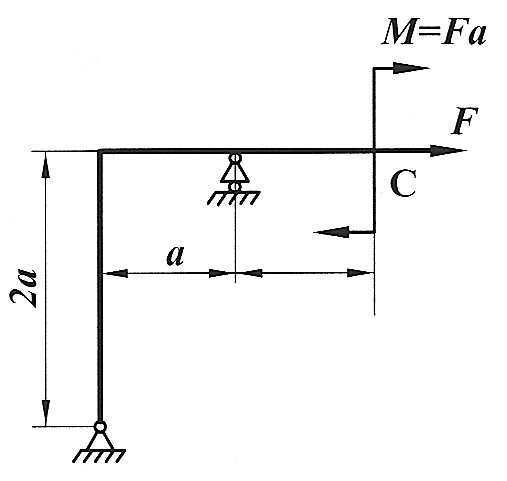
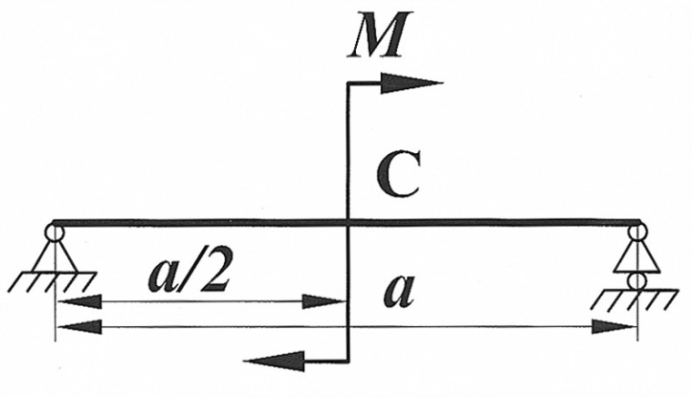
| Определить способом Верещагина величину вертикального, горизонтального перемещения и угол поворота сечения С статически определимой рамы.
F, a, E, 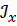 даны. даны.
|
Задача 23
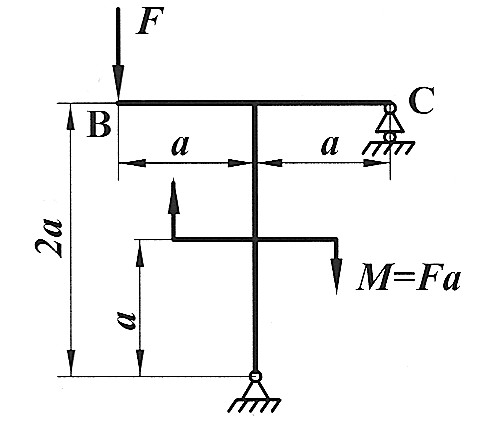
| Определить способом Верещагина величину вертикального перемещения сечения В и угол поворота сечения С статически определимой рамы.
F, a, E, 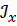 даны. даны.
|
Задача 24
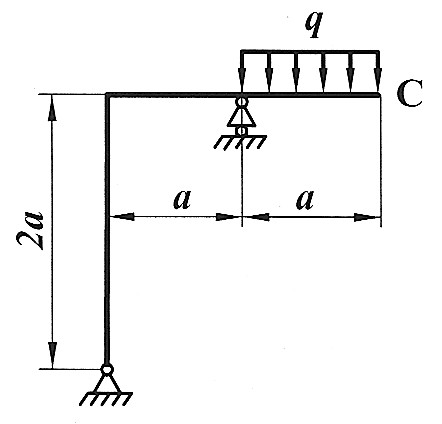
| Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С статически определимой рамы.
F, a, E, 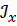 даны. даны.
|
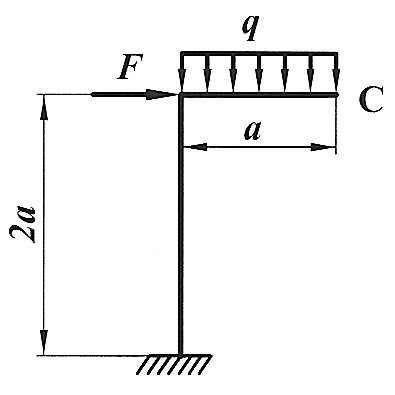
Задача 25
Определить способом Верещагина величину вертикального, горизонтального перемещения и угол поворота сечения С статически определимой рамы. F , a , E , 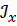 даны. даны.
| 
|
Задача 2 6
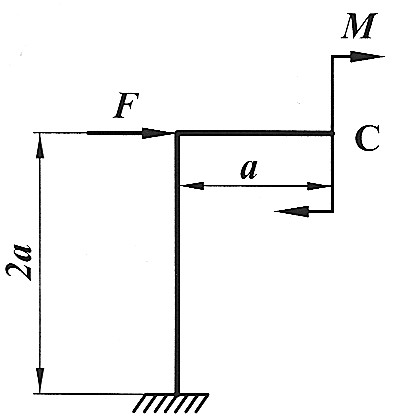
Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С статически определимой рамы.
F, a, E, 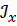 даны. даны.
| 
|
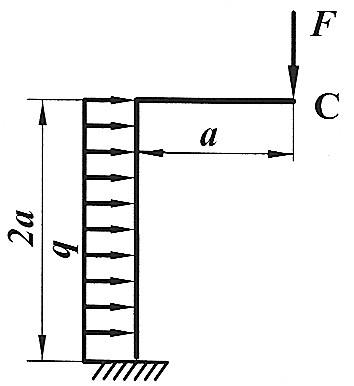
Задача 2 7
Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С статически определимой рамы. F , a , E , 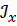 даны. даны.
| 
|
Задача 28
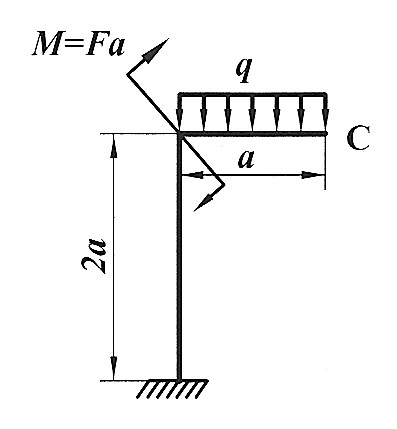
| Определить способом Верещагина величину вертикального, горизонтального перемещения и угол поворота сечения С статически определимой рамы. F, a, E, 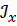 даны. даны.
|
Задача 2 9
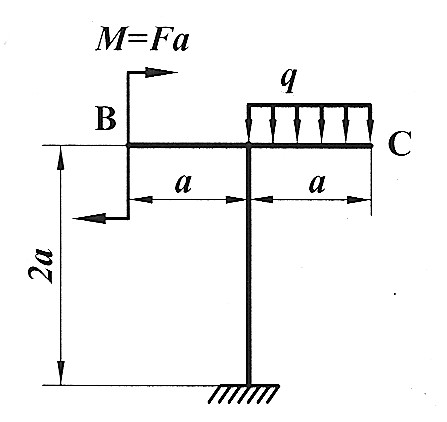
| Определить способом Верещагина величину вертикального перемещения сечения В и угол поворота сечения С статически определимой рамы. F , a , E , 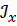 даны. даны.
|
Задача 30
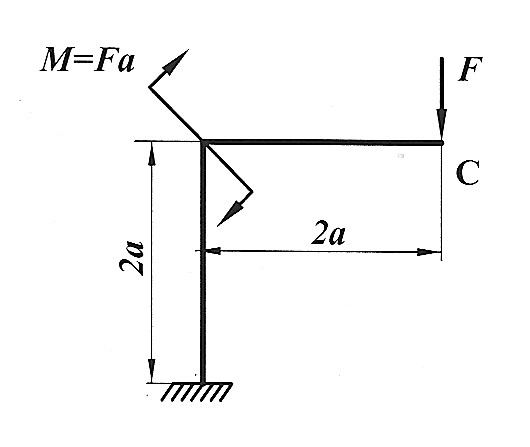
| Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С статически определимой рамы. F , a , E , 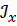 даны. даны.
|
Дата: 2019-03-05, просмотров: 660.