(рам, многопролетных балок)
1. Определяем степень статической неопределимости. Для этого составляются все возможные уравнения статики. Для плоской системы максимальное их число равно трем. Тогда степень статической неопределимости «k» вычисляется как
k = n -3,
где n – число связей.
2. Выбирается основная система. Для этого удаляются все лишние связи, как внешние, так и внутренние. А их действие заменяется силами или парами сил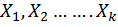 
. Система становится статически определимой.
3. Записываются канонические уравнения метода сил. Их число должно быть равно степени статической неопределимости k.
4. Вычисляются коэффициенты канонических уравнений метода сил. Для выбранной основной системы строятся эпюры изгибающих моментов от единичных нагрузок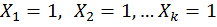 
и заданной внешней нагрузки, последовательно. Коэффициенты 
находятся путем «перемножения» соответствующих эпюр от единичных нагрузок. Например, коэффициент 
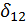определяется как результат перемножения площади эпюры 
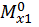на соответствующие ординаты эпюры 
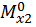. Причем необходимо помнить, что 
.
Грузовые коэффициенты 
находятся путем «перемножения» грузовой эпюры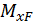 
на соответствующую эпюру от единичных нагрузок 
.
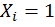5. Определяются неизвестные 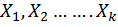. Для этого решается система канонических уравнений. Таким образом, статическая неопределимость раскрыта.
6. Основная система нагружается нагрузками как внешними силами F, так и неизвестными 
Определяются остальные неизвестные реакции и строится окончательная эпюра изгибающих моментов.
7. Производится проверка расчета. Обычно производится статическая и деформационная проверка. При статической проверке рассматривается равновесие отсеченной части рамы (чаще узлов рамы) под действием внешних и внутренних сил. При деформационной проверке производится перемножение по способу Верещагина эпюры изгибающих моментов, построенной для заданной рамы, на любую из эпюр изгибающих моментов от единичной нагрузки. В результате перемножения при жестких связях должны получить ноль.
8. Определяются размеры поперечного сечения стержней рамы из условия прочности:
9. Определяются перемещения сечений рамы. Для этого в сечении, где определяются перемещения, по его направлению прикладывается сила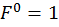 
, если требуется определить линейное перемещение, или единичный момент 
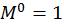, если требуется определить угловое перемещение, и строится эпюра изгибающих моментов (единичная эпюра). Повторим, раскрывать статическую неопределимость уже не требуется. Можно использовать ранее выбранную основную систему и к ней приложить единичную нагрузку, а можно выбрать другую, если вычисления искомого перемещения будут проще.
Пример расчета статически неопределимой балки
Пример 1. Раскрыть статическую неопределимость, построить эпюры изгибающих моментов и поперечных сил для балки, изображенной на рис. 16. Составить условие прочности, если
а=1м, d=0,02 м, М=25 кНм, q=20 кН/м, [σ]=160 МПа.
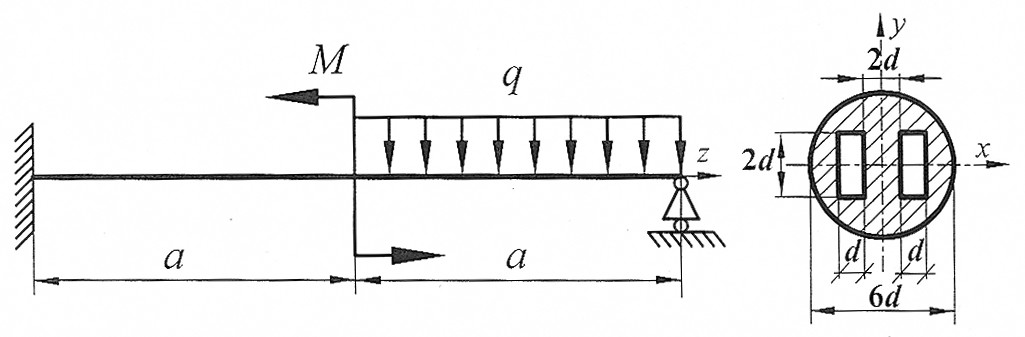
Рис. 16
Решение.
Определяем степень статической неопределимости.
Для этого обозначим реакции опор (рис. 17, а) и составим уравнения статики:
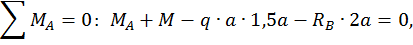
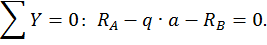
Данная балка 1 раз статически неопределимая, так как имеем 3 неизвестных и только 2 независимых уравнений статики:
k = 3– 2 = 1.
Выбираем основную систему, удаляя «лишнюю» связь.
За лишнее закрепление примем шарнирно-подвижную опору В. Основная система балки показана на рис. 17, б. «Лишнюю» связь заменяем силой Х1 (рис. 17, в).
Записываем каноническое уравнение метода сил:
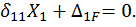
Отброшенная связь не допускают перемещений, поэтому в правой части уравнения стоит ноль.
Вычисляем коэффициенты канонических уравнений по способу Верещагина. Рассматриваемая балка работает главным образом на изгиб, поэтому сдвигом балки будем пренебрегать. Коэффициенты канонического уравнения вычисляем по формуле
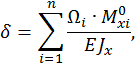
где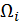 
– площадь эпюры изгибающего момента от заданной нагрузки
на i-м участке (её часто называют грузовой площадью);
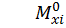– ордината эпюры изгибающих моментов от единичной
нагрузки, взятая под центром тяжести первой эпюры;
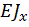– жесткость балки.
Предварительно строим эпюры изгибающих моментов от заданной внешней нагрузки и единичной нагрузок (Х1=1) (рис. 17, д, ж).
Построим эпюры изгибающего момента 
от внешней нагрузки (грузовую эпюру, рис. 17, д):
Первый участок: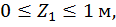 
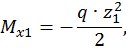
при 
:
,
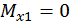при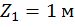 
:
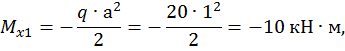
Второй участок: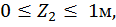 
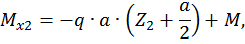
при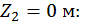 
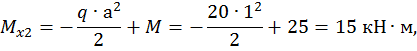
при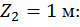 
.
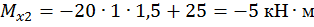Построим эпюры изгибающего момента 
от единичной нагрузки (единичную эпюру, рис. 17, г):
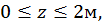
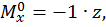
при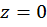 
:
,
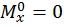при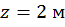 
:
.
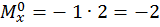Коэффициент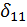 
определяем “перемножением” эпюры 
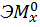самой на себя.
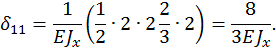
Грузовой коэффициент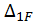 
находим “перемножением” грузовой эпюры 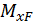на эпюру от единичной нагрузки. Для этого грузовую эпюру разбиваем на два обычных треугольника, один сверху от оси z, другой снизу от оси z, и на «параболический» треугольник.
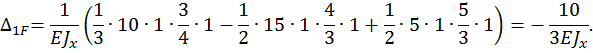
Определяем неизвестную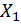 
, решая каноническое уравнение
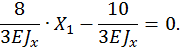
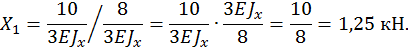
Таким образом, статическая неопределимость раскрыта.
Построим эпюру поперечных сил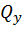 
(рис. 18, б).
Первый участок: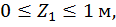
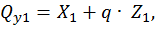
при :
,
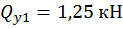при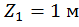 
:
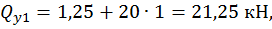
Второй участок: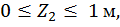 
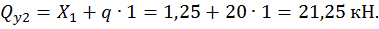
Построим эпюру изгибающих моментов (рис. 18, в).
Первый участок: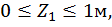 
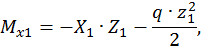
при :
,
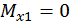при :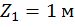
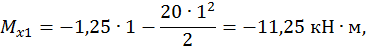
Второй участок: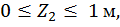
,
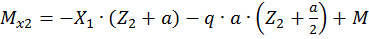при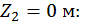
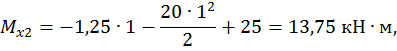
при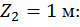
.
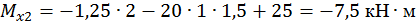Проверка расчета. Обычно проводится деформационная проверка. При деформационной проверке производится перемножение по способу Верещагина эпюры изгибающих моментов, построенной для заданной балки, на эпюру изгибающих моментов от единичной нагрузки (рис. 18, в, д). Для этого грузовую эпюру разбиваем на три треугольника, один сверху от оси z, два снизу от оси z, и фигуру, очерченную квадратичной параболой.
В результате перемножения вертикальное перемещение должно быть равно нулю.
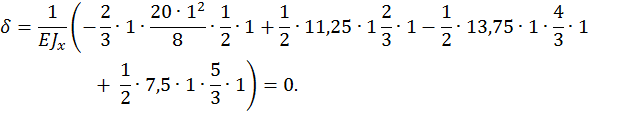
Деформационная проверка подтвердила правильность расчета.
Составим условие прочности по формуле
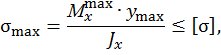
где
,
.
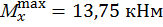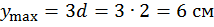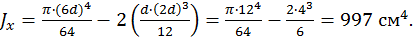
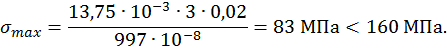
Таким образом, условие прочности выполняется.
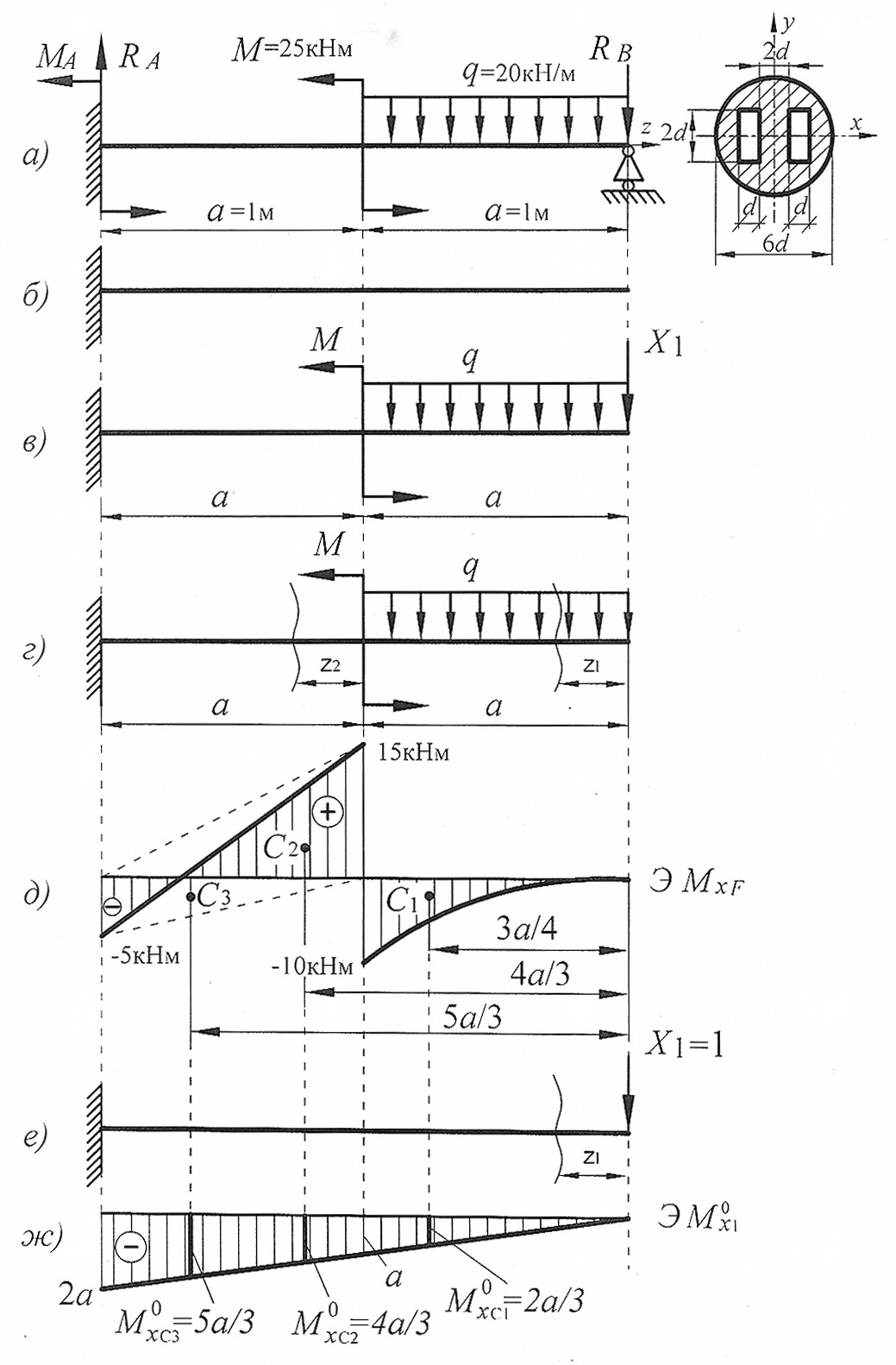Рис. 17
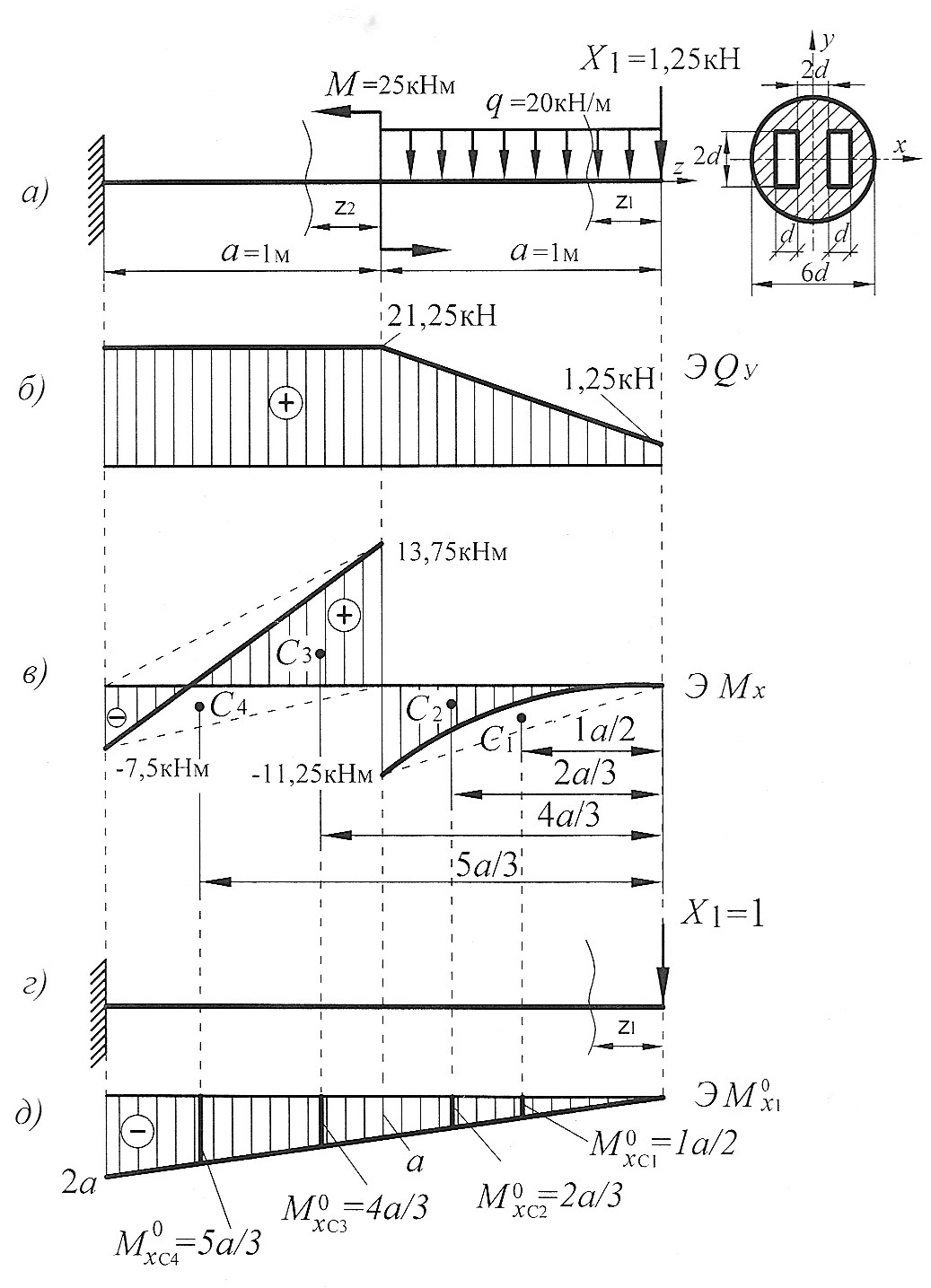
Рис. 18
Пример расчета статически неопределимой рамы
Пример 1. Раскрыть статическую неопределимость рамы (рис. 19). Построить эпюры продольных, поперечных сил и изгибающих моментов. Составить условие прочности, из условия прочности подобрать размеры поперечного сечения. Найти горизонтальное перемещения сечения С и угол поворота сечения D. Дано: F =20 кН, а=2 м, М= F 
a,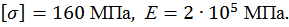 
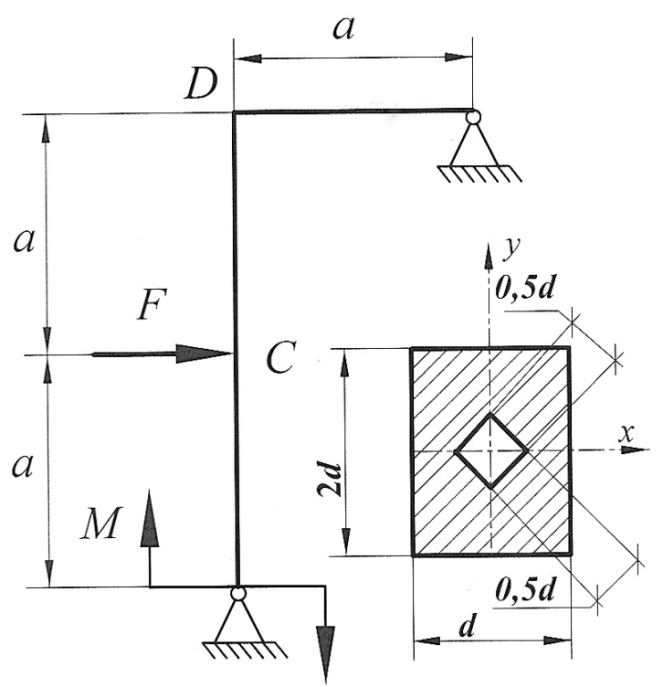
Рис. 19
Решение.
Определяем степень статической неопределимости.
Для этого обозначим реакции опор (рис. 20, а) и составим уравнения статики:
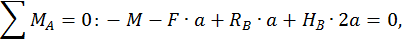
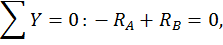
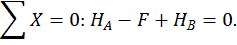
Данная рама 1 раз статически неопределимая, так как имеем 4 неизвестных и только 3 независимых уравнений статики:
k = 4– 3 = 1.
Выбираем основную систему, удаляя «лишнюю» связь.
За «лишнее» закрепление примем горизонтальное закрепление в шарнирно-неподвижной опоре В. Заменим шарнирно-неподвижную опору шарнирно-подвижной. Основная система балки показана на рис. 20, б. «Лишнюю» связь заменяем силой Х1 (рис. 20, в).
Записываем каноническое уравнение метода сил:
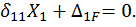
Отброшенная связь не допускает горизонтального перемещения, поэтому в правой части уравнения стоит ноль.
Вычисляем коэффициенты канонических уравнений по способу Верещагина. Рассматриваемая рама работает главным образом на изгиб, поэтому сдвигом и растяжением (сжатием) рамы будем пренебрегать. Коэффициенты канонического уравнения вычисляем по формуле
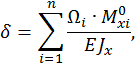
где 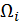– площадь эпюры изгибающего момента от заданной нагрузки
на i -м участке (её часто называют грузовой площадью);
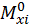– ордината эпюры изгибающих моментов от единичной
нагрузки, взятая под центром тяжести первой эпюры;
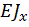– жесткость балки.
Предварительно строим эпюры изгибающих моментов от заданной внешней нагрузки (рис. 20, г) и единичной нагрузки Х1=1 (рис. 20, д).
Построим эпюры изгибающего момента от внешней нагрузки (грузовую эпюру, рис. 21, а). Для этого определим опорные реакции из уравнений статики:
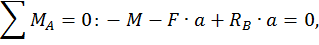
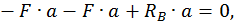
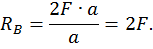
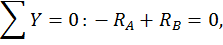
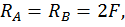
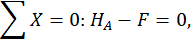
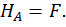
Составим выражения для изгибающих моментов на каждом участке.
Первый участок: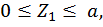 
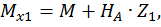
при :
,
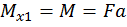при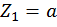 
:
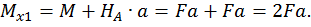
Второй участок: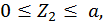 
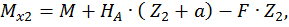
при 
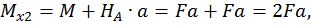
при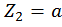 
:
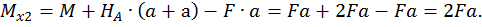
Третий участок: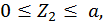
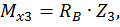
при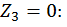 
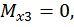
при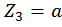 
:
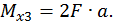
Построим эпюры изгибающего момента от единичной нагрузки Х1 =1 (единичную эпюру, рис. 21, б). Для этого определим опорные реакции:
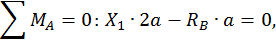
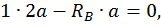
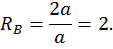
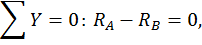
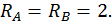
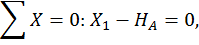
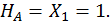
Составим выражения для изгибающих моментов на каждом участке.
Первый участок: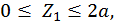 
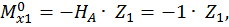
при :
,
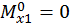при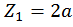 
:
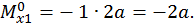
Второй участок: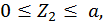
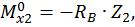
при
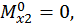
при :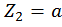
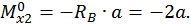
Коэффициент 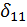определяем «перемножением» эпюры 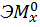самой на себя.
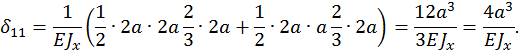
Грузовой коэффициент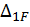 
находим «перемножением» грузовой эпюры 
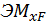(см. рис. 21, а) на эпюру от единичной нагрузки 
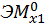(рис. 21б). Для этого грузовую эпюру разбиваем на три треугольника и на прямоугольник (см. рис. 21, а).
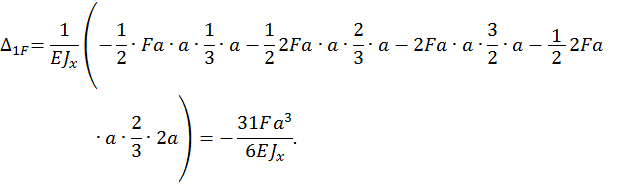
Определяем неизвестную 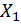, решая каноническое уравнение
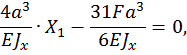
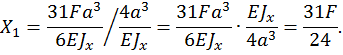
Таким образом, статическая неопределимость раскрыта.
Строим эпюры продольных, поперечных сил и изгибающих моментов. Для этого определим опорные реакции из уравнений статики:
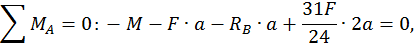
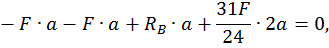
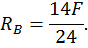
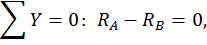
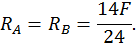
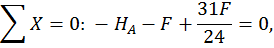
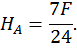
Построим эпюру продольных сил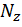 
(рис. 22, а).
Первый участок: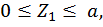
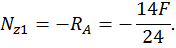
Второй участок: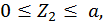
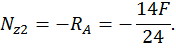
Третий участок: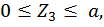 
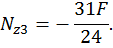
Построим эпюру поперечных сил 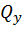(рис. 22, б).
Первый участок: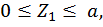
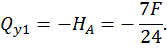
Второй участок: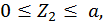
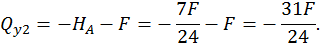
Третий участок: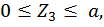
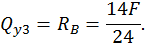
Построим эпюру изгибающих моментов (рис. 22, в).
Первый участок: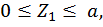
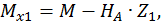
при :
,
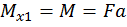при :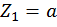
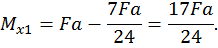
Второй участок: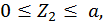
,
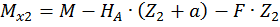при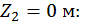
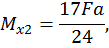
при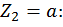 
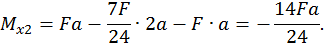
Третий участок: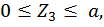
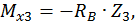
при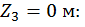 
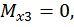
при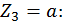 
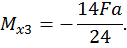
Проверка расчета. Обычно проводится деформационная проверка. При деформационной проверке производится перемножение по способу Верещагина эпюры изгибающих моментов, построенной для заданной рамы (рис 22в), на эпюру изгибающих моментов от единичной нагрузки (рис. 22, г). Для этого грузовую эпюру разбиваем на пять треугольников (см. рис. 22, в).
В результате перемножения горизонтальное перемещение должно быть равно нулю.
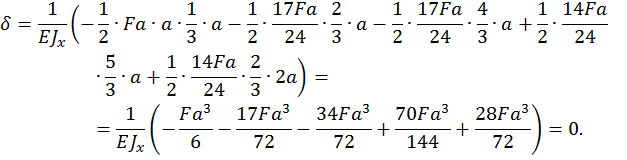
Деформационная проверка подтвердила правильность расчета.
Составим условие прочности по формуле
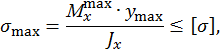
где 
,
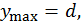
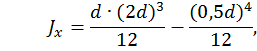
тогда
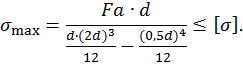
Подставив значения F =20 кН, а=2 м,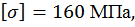 
из условия прочности определим размеры поперечного сечения:
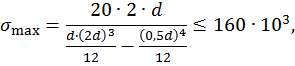
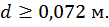
Принимаем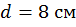 
, 
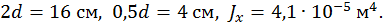
Определим горизонтальное перемещение сечения С. Для этого строим эпюру изгибающих моментов (единичную эпюру рис. 23, б) от горизонтальной единичной силы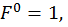 
приложенной в точке С (рис. 23, а). Для этого определим опорные реакции из уравнений статики:
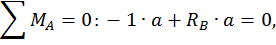
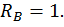
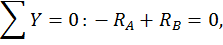
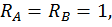
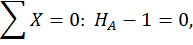
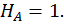
Составим выражения для изгибающих моментов на каждом участке.
Первый участок: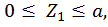 
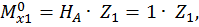
при :
,
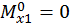при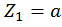 
:
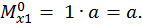
Второй участок: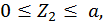
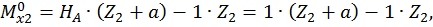
при
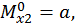
при :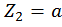
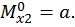
Третий участок: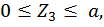
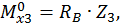
при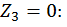
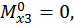
при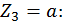
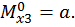
Для определения горизонтального перемещения сечения С перемножаем данную единичную эпюру (см. рис. 23, б) и эпюру изгибающих моментов для заданной рамы (рис. 22, в):
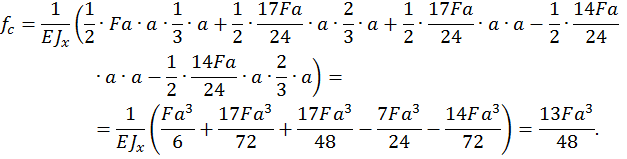
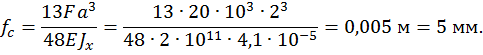
Определим угол поворота сечения D. Для этого строим эпюру изгибающих моментов, единичную эпюру (рис. 23, г) от единичного момента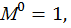 
приложенного в сечении D (см. рис. 23, в). Для этого определим опорные реакции из уравнений статики:
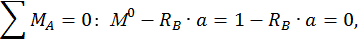
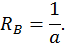
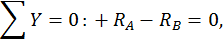
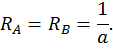
Составим выражения для изгибающих моментов на каждом участке.
Первый участок: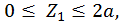 
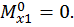
Второй участок: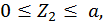
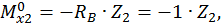
при
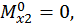
при :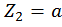
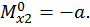
Для определения угла поворота сечения D перемножаем данную единичную эпюру (см. рис. 23, г) и эпюру изгибающих моментов для заданной рамы (см. рис. 22, в):
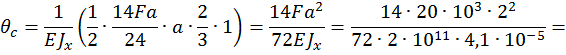
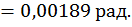
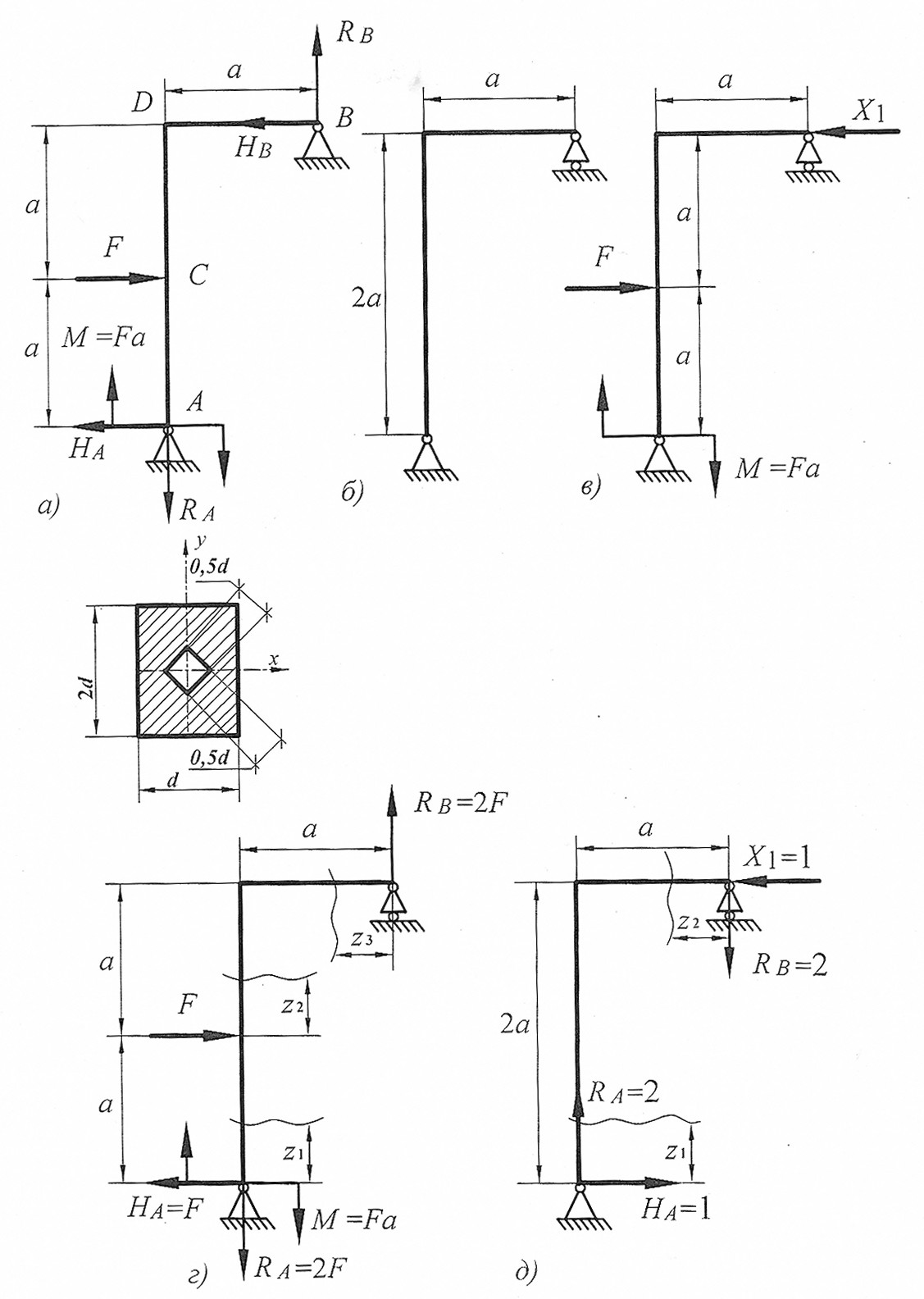
Рис. 20
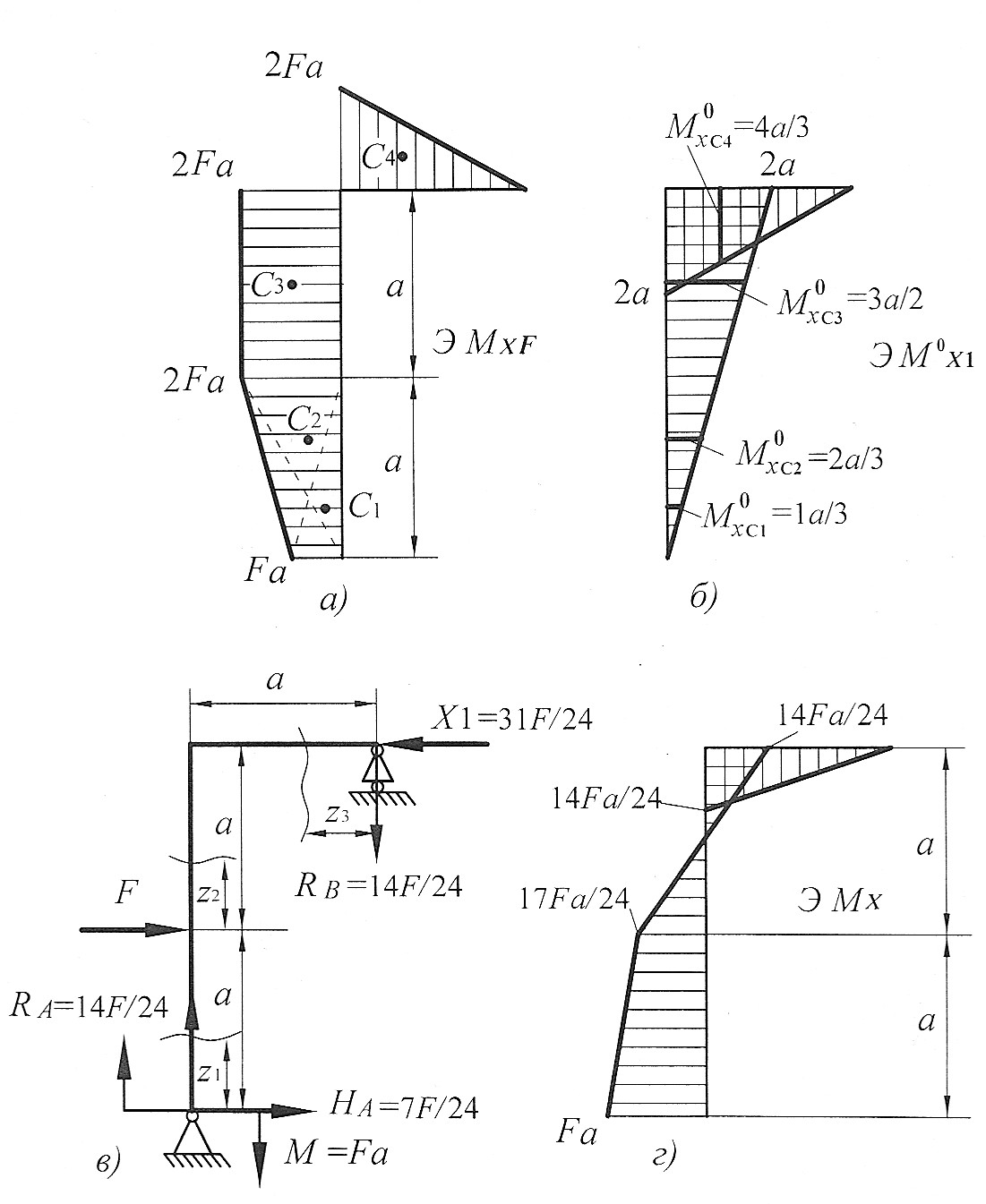
Рис. 21
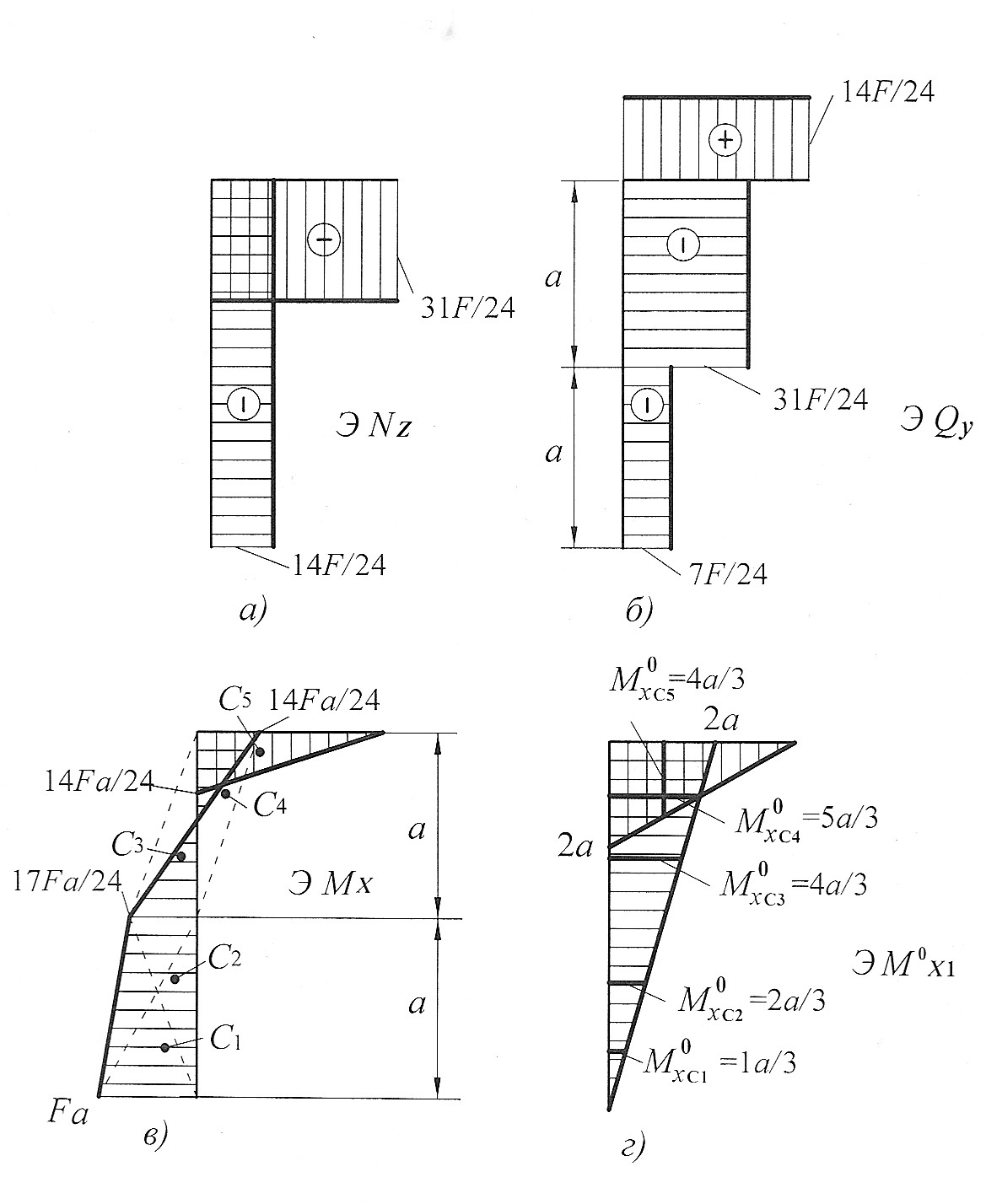
Рис. 22
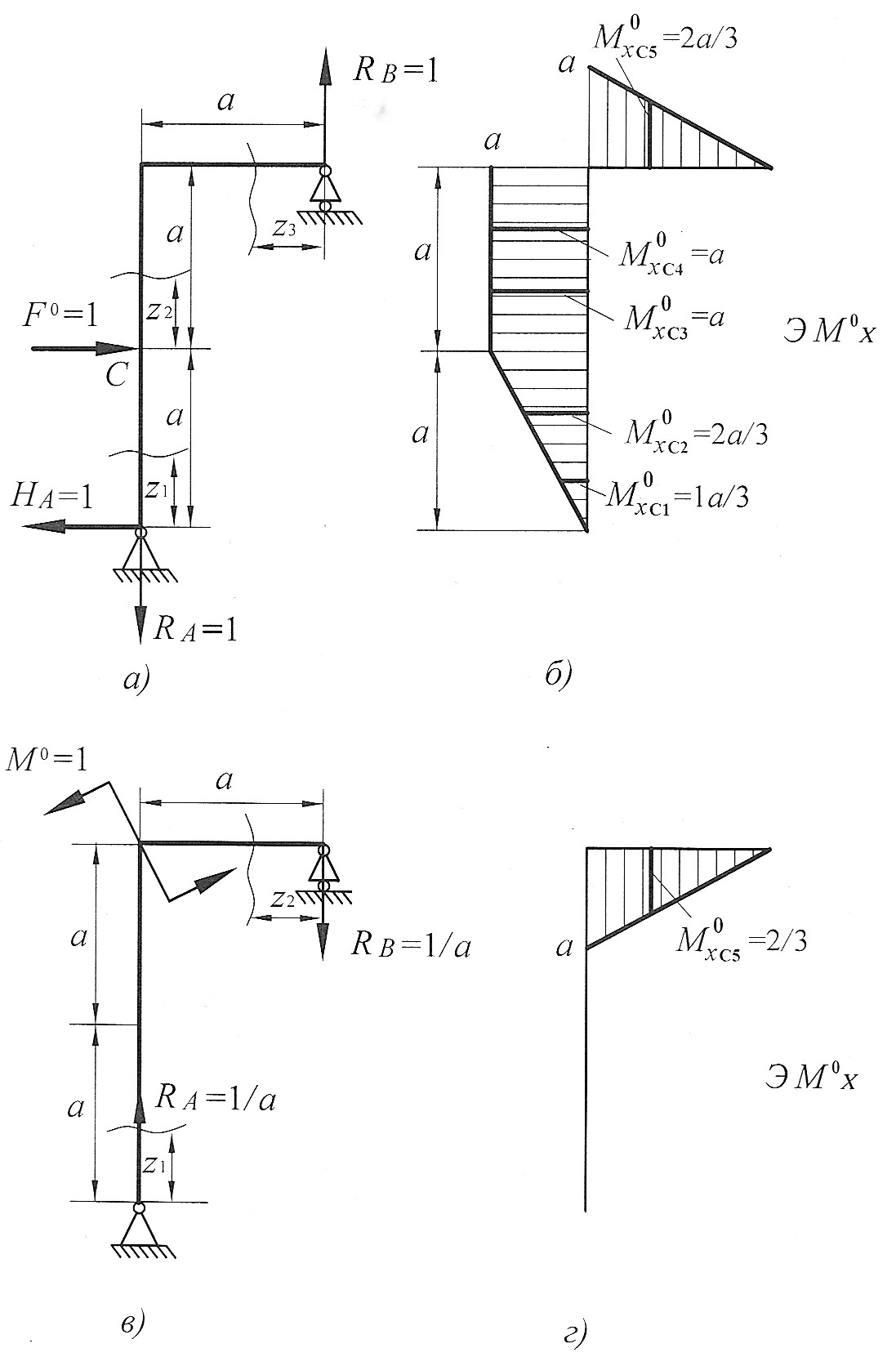
Рис. 23
Дата: 2019-03-05, просмотров: 217.
