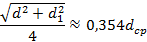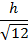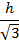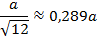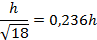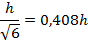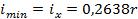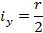И.С. Шеронина, С.А. Петерсон,
А.С. Нефедов
МЕТОДЫ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ
В СТЕРЖНЕВЫХ СИСТЕМАХ
Ярославль
2018
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Ярославский государственный технический университет»
И.С. Шеронина, С.А. Петерсон, А.С. Нефедов
МЕТОДЫ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ
В СТЕРЖНЕВЫХ СИСТЕМАХ
Рекомендовано
научно-методическим советом университета
в качестве учебного пособия
Ярославль
Издательский дом ЯГТУ
2018
УДК 539
ББК 38.112
Ш49
Шеронина, И.С.
Ш49 Методы определения перемещений в стержневых системах: учебное пособие / И.С. Шеронина, С.А. Петерсон, А.С. Нефедов. – Ярославль: Издат. дом ЯГТУ, 2018. – 92 с.
ISBN
Учебное пособие разработано по курсам «Сопротивление материалов» и «Техническая механика» в соответствии с государственным общеобразовательным стандартом высшего профессионального образования. В работе изложены основные теоретические положения по темам «Методы определения перемещений при изгибе в стержневых системах» и «Статически неопределимые системы». Приведены примеры решения типовых задач по данным темам и предложены задачи для самостоятельного решения с целью проверки степени усвоения материала данных тем.
Рекомендовано для студентов механических и строительных направлений очной и заочной формы обучения.
Рецензенты: АО Ярижком (А.Ю. Юдин, канд. техн. наук, зам. директора); В.П. Панченко, канд. техн. наук, директор по науке и внедрению новых технологий ООО «СОТпрофи».
_____________________________________________________
Редактор Л.С. Кокина
План 2018
Подписано в печать 27.04.2018. Формат 60х84 1/16. Бумага белая.
Печать ризограф. Усл. печ. л. 5,35. Уч.-изд. л. 5,33. Тираж . Заказ
Ярославский государственный технический университет
150023, Ярославль, Московский пр., 88
Издательский дом ЯГТУ
150000, Ярославль, ул. Советская, 14а
_____________________________________________________
| ISBN | Ярославский государственный технический университет, 2018 |
Оглавление
| ВВЕДЕНИЕ.................................................................................................. | 5 |
| 1. МЕТОД НАЧАЛЬНЫХ ПАРАМЕТРОВ.......................................... | 6 |
| 1.1. Перемещение при изгибе. Универсальное уравнение упругой линии балки........................................................................... | 6 |
| 1.2. Порядок определения перемещений при изгибе по методу начальных параметров........................................................ | 9 |
| 1.3. Примеры определения перемещений при изгибе по методу начальных параметров. .................................................... | 9 |
| 2. МЕТОД МОРА................................................................................. | 12 |
| 2.1. Основные положения............................................................. | 12 |
| 2.2. Порядок определения перемещений при изгибе по методу Мора....................................................................................... | 13 |
| 2.3. Пример определения перемещений по методу Мора......... | 14 |
| 3. МЕТОД (ПРАВИЛО) ВЕРЕЩАГИНА.......................................... | 19 |
| 3.1. Основные положения правила Верещагина......................... | 19 |
| 3.2. Порядок определения перемещений по правилу Верещагина................................................................................... | 22 |
3.3. Примеры разбиения сложных площадей 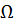 фигур
изгибающих моментов от внешней нагрузки и
вычисления произведения фигур
изгибающих моментов от внешней нагрузки и
вычисления произведения 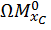 для случаев, в которых
единичная эпюра трапеция.......................................................... для случаев, в которых
единичная эпюра трапеция..........................................................
| 23 |
| 3.4. Пример определения перемещений по правилу Верещагина………………………………………………........... | 29 |
| 4. ЗАДАЧИ ДЛЯ ПРОВЕРКИ СТУДЕНТАМИ СТЕПЕНИ УСВОЕНИЯ МАТЕРИАЛА РАЗДЕЛА «ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ПРИ ИЗГИБЕ»…………………………………. | 33 |
| 5. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ПРИ ИЗГИБЕ……………………………………………………………… | 43 |
| 5.1. Основные положения…………………………………….. | 43 |
| 5.2. Порядок расчета статически неопределимых систем (рам, многопролетных балок)………………………………... | 45 |
| 5.3. Пример расчета статически неопределимой балки…….. | 46 |
| 5.4. Пример расчета статически неопределимой рамы……... | 53 |
| 5.5. Использование свойств симметрии при раскрытии статической неопределимости……………………………...... | 65 |
| 5.6. Пример расчета симметричной статически неопределимой рамы, нагруженной кососимметричной нагрузкой…………………………………………………......... | 67 |
| 6. ЗАДАЧИ ДЛЯ ПРОВЕРКИ СТУДЕНТАМИ СТЕПЕНИ УСВОЕНИЯ МАТЕРИАЛА РАЗДЕЛА «СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ | 75 |
| Контрольные вопросы......................................................................... | 85 |
| Заключение........................................................................................... | 86 |
| Библиографический список........................................................................ | 87 |
| Приложение А. Двутавры стальные горячекатаные. Сортамент по ГОСТ 8239–89..................................................................... | 88 |
| Приложение Б. Швеллеры стальные горячекатаные. Сортамент по ГОСТ 8240–89..................................................................... | 89 |
| Приложение В. Площади, координаты центров тяжести для основных форм сечений....................................................................... | 90 |
| Приложение Г. Моменты инерции, моменты сопротивления для основных форм сечений....................................................................... | 91 |
| Приложение Д. Радиусы инерции для основных форм сечений............. | 92 |
ВВЕДЕНИЕ
Во многих случаях при проектировании элементов конструкций недостаточно оценки их прочности. На первый план может выходить требование обеспечения заданной жесткости.
Для проверки жесткости конструкции необходимо научиться определять максимальные перемещения и перемещения конкретных точек или сечений её элементов. Также умение определять перемещение требуется для раскрытия статической неопределимости.
В данном пособии представлены три наиболее широко используемых метода определения перемещений: метод начальных параметров, метод Мора, способ (правило) Верещагина. В работе рассмотрены основные теоретические положения этих методов. Предложены планы определения перемещений каждым методом. Подробно разобраны примеры решения задач по определению перемещений в элементах вида "балка", "рама". Предложены задачи для самостоятельного решения с целью проверки степени усвоения материала.
В пособии представлен один из основных методов раскрытия статической неопределимости – метод сил в канонической его трактовке. Также в работе студентам предложен план раскрытия статической неопределимости методом сил. Решены статически неопределимые задачи данным методом (статически неопределимая балка, статически неопределимая рама). В работе даны рекомендации по использованию свойств симметрии при раскрытии статической неопределимости и рассмотрен пример решения симметричной статически неопределимой рамы, нагруженной кососимметричной нагрузкой. Далее студентам предложены статически неопределимые задачи для самостоятельного решения.
Пособие предназначено для подготовки студентов к выполнению расчётно-проектировочных и лабораторных работ, к решению экзаменационных задач по представленным в работе темам.
МЕТОД НАЧАЛЬНЫХ ПАРАМЕТРОВ
Упругой линии балки
Под действием внешних сил, вызывающих прямой поперечный изгиб, прямая ось балки искривляется, превращаясь в кривую линию, которая носит название упругой линии балки или изогнутой оси балки.
При деформации центр тяжести поперечного сечения получает линейное перемещение, перпендикулярное к недеформированной оси балки, которое называется прогибом и обозначается f ( y ). При этом поперечное сечение, оставаясь плоским, поворачивается вокруг нейтральной оси х на некоторый угол 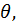 который называется углом поворота сечения (рис. 1).
который называется углом поворота сечения (рис. 1).
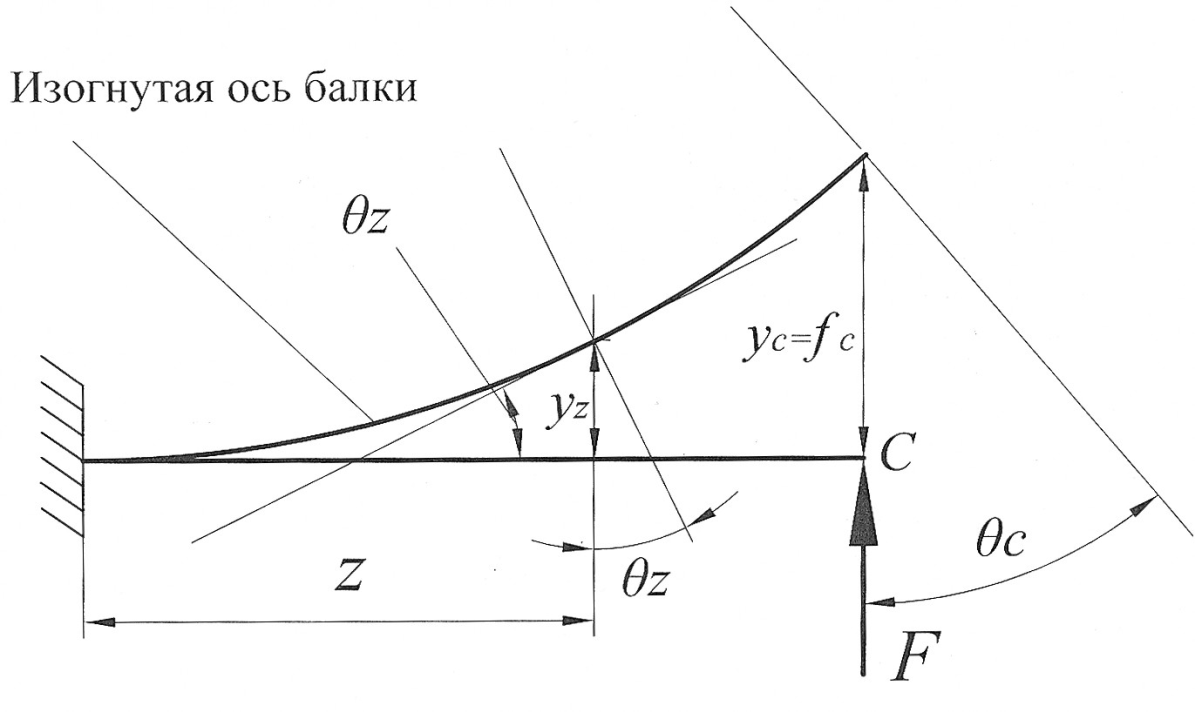
Рис. 1
Из аналитической геометрии известна прямая связь между тангенсом угла наклона касательной и первой производной от уравнения этой кривой. Следовательно,

Поскольку при малых углах поворота 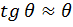 , то выражение (1) может быть записано как
, то выражение (1) может быть записано как

С одной стороны, кривизна изогнутой оси балки при чистом изгибе может быть определена из выражения

Здесь  – изгибающиймомет,
– изгибающиймомет, 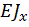 – жесткость балки при изгибе.
– жесткость балки при изгибе.
С другой стороны, из математики известно соотношение между кривизной любой линии и её производными:

Для малых перемещений 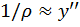 . Тогда приближенное дифференциальное уравнение изогнутой оси балки примет вид
. Тогда приближенное дифференциальное уравнение изогнутой оси балки примет вид

или

Интегрируя данное соотношение два раза, получаем уравнения для определения углов поворота и прогибов:
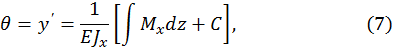
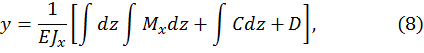
где C и D – постоянные интегрирования, которые определяются из условия деформации на опорах и на границах участков.
Определение перемещений методом непосредственного интегрирования приближенного дифференциального уравнения изогнутой оси для случая балок с большим количеством участков по изгибающему моменту сопряжено со значительными трудностями, поскольку приходится определять большое количество произвольных постоянных интегрирования. Если балка имеет несколько участков по изгибающему моменту, то для каждого участка приходится составлять свое уравнение  , а после его интегрирования еще определять постоянные С и D, число которых равно удвоенному количеству участков. Задача становится весьма трудоемкой уже при трех участках.
, а после его интегрирования еще определять постоянные С и D, число которых равно удвоенному количеству участков. Задача становится весьма трудоемкой уже при трех участках.
Однако, используя специальные приемы, можно уменьшить число постоянных интегрирования до двух, то есть свести задачу к нахождению угла поворота 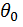 и прогиба
и прогиба 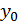 в начале отсчета координат. Такой метод определения перемещения называется методом начальных параметров, а уравнение для определения прогибов в произвольном сечении называется универсальным уравнением упругой линии балки. Например, для балки (рис. 2) уравнения метода начальных параметров имеют вид
в начале отсчета координат. Такой метод определения перемещения называется методом начальных параметров, а уравнение для определения прогибов в произвольном сечении называется универсальным уравнением упругой линии балки. Например, для балки (рис. 2) уравнения метода начальных параметров имеют вид
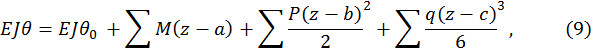
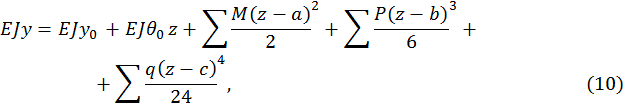
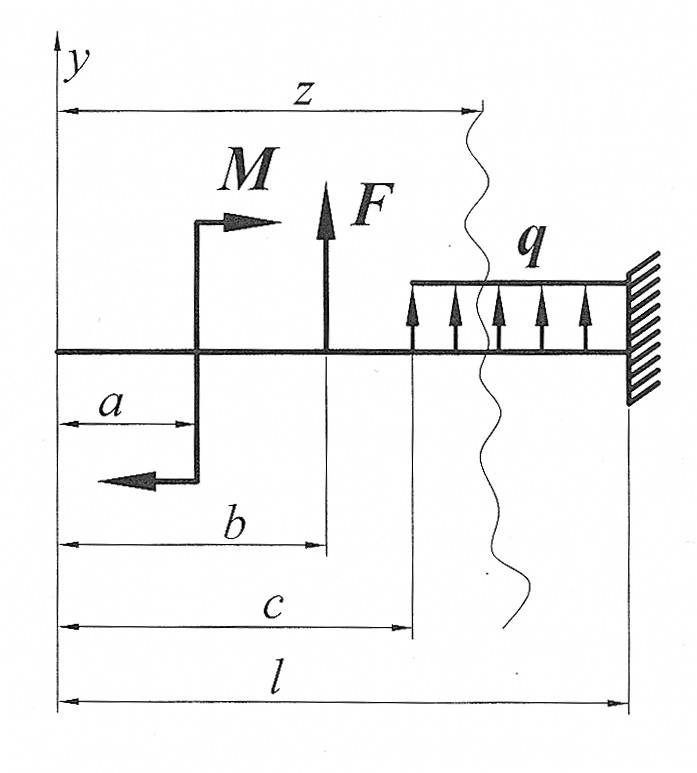
Рис. 2
В уравнения (9) и (10) включаются с соответствующими знаками все внешние нагрузки, расположенные между началом координат и сечением с абсциссой z на последнем правом участке. Внешние нагрузки, показанные на рисунке, включены в универсальные уравнения со знаком плюс, нагрузки противоположного направления включаются в уравнения со знаком минус. Важно отметить, что уравнения (9), (10) будут справедливы, если распределенная нагрузка q распространяется до сечения, где определяются перемещения. Если распределенная нагрузка q не доходит до данного сечения, её следует продолжить, одновременно добавив нагрузку, равную по величине, но противоположную по направлению. При вычислении перемещений в конкретном сечении учитываются только те нагрузки, которые расположены левее этого сечения.
Начальные параметры 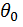 и
и 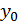 определяются из условий закрепления балки.
определяются из условий закрепления балки.
Недостаток универсальных уравнений состоит в том, что их нельзя непосредственно использовать для определения перемещений в балках, имеющих различную жесткость 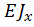 на разных участках. Кроме того, эти уравнения совсем неприменимы к балкам, имеющим непрерывно изменяющуюся по длине жесткость. В этих случаях следует применять общий метод определения перемещений – метод Мора.
на разных участках. Кроме того, эти уравнения совсем неприменимы к балкам, имеющим непрерывно изменяющуюся по длине жесткость. В этих случаях следует применять общий метод определения перемещений – метод Мора.
1.2. Порядок определения перемещений методом начальных параметров
1. Выбираем начало координат в крайнем левом сечении.
2. Определяем реакции опор.
3. Для произвольного сечения на последнем правом участке записываем оба уравнения для прогибов и углов поворота.
4. Находим начальные параметры (прогиб 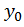 и угол поворота
и угол поворота 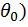 в начале отсчета. Если в начале отсчета расположена жесткая заделка, то начальные параметры будут равны нулю (
в начале отсчета. Если в начале отсчета расположена жесткая заделка, то начальные параметры будут равны нулю ( 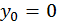 и
и 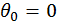 ). Если в начале отсчета окажется шарнирная опора, то прогиб в начале отсчета будет равен нулю (
). Если в начале отсчета окажется шарнирная опора, то прогиб в начале отсчета будет равен нулю ( 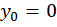 ). В общем случае записываем выражения для определения прогибов в сечениях с шарнирными опорами и, приравняв их нулю, находим
). В общем случае записываем выражения для определения прогибов в сечениях с шарнирными опорами и, приравняв их нулю, находим 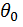 и
и 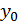 .
.
6. Вычисляем перемещения в заданных сечениях, подставляя в уравнения (пункт 3) конкретные значения координат этих сечений и учитывая только те нагрузки, которые расположены левее соответствующих сечений.
1.3. Примеры определения перемещений при изгибе
Пример 1.
Для консольной балки (рис. 3) постоянной жесткости 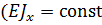 ) необходимо определить угол поворота
) необходимо определить угол поворота 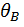 и прогиб
и прогиб 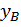 на свободном конце.
на свободном конце.
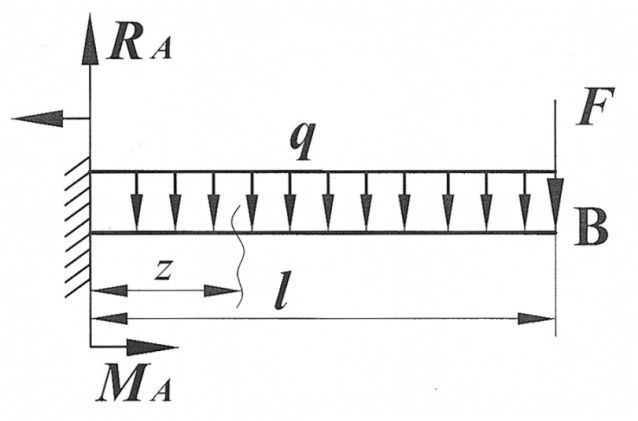
Рис. 3
Решение.
Для определения опорных реакций 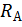 и
и 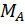 составим два уравнения статики:
составим два уравнения статики:
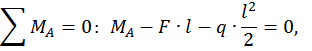
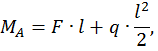
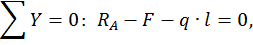
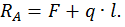
Запишем универсальное уравнение упругой линии балки для произвольного сечения с координатой z.
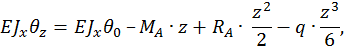
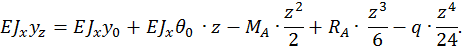
Учитывая, что  и
и 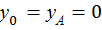 и подставляя
и подставляя 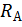 и
и 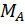 в полученные уравнения, имеем:
в полученные уравнения, имеем:
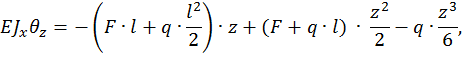
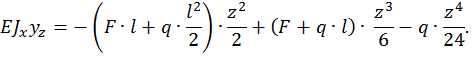
Для определения искомых перемещений 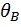 и
и 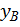 в полученные уравнения необходимо подставить z=l , тогда:
в полученные уравнения необходимо подставить z=l , тогда:
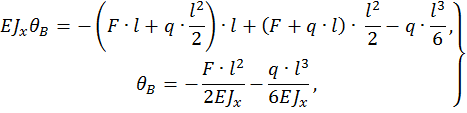
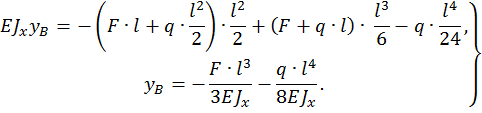
Пример 2.
Определить прогиб в сечении D, угол поворота на опоре B балки, изображенной на рис. 4, при 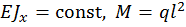 .
.
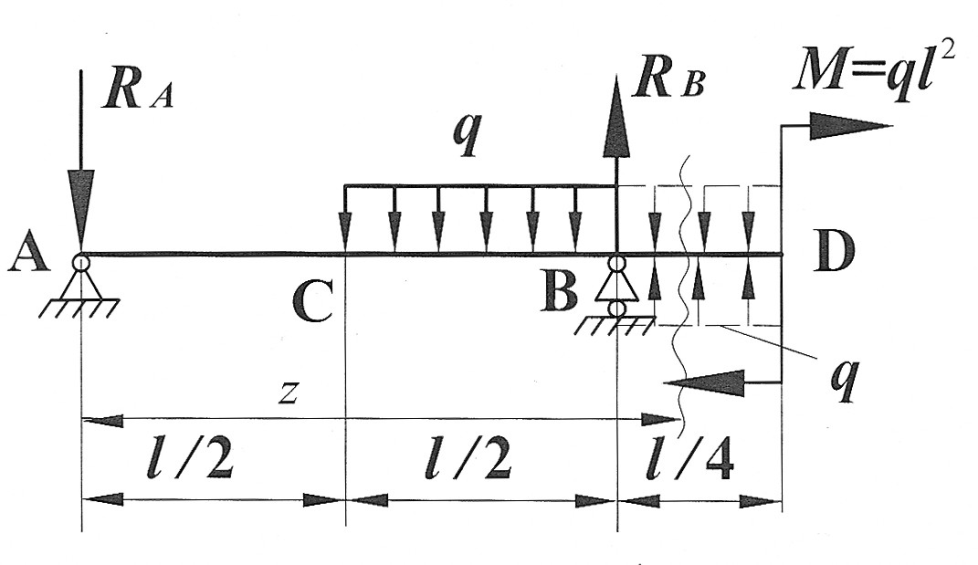
Рис. 4
Для определения реакций опор 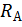 и
и 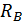 составим два уравнения статики:
составим два уравнения статики:
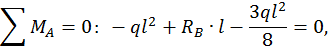
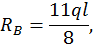
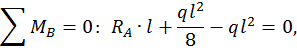
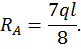
Для произвольного сечения с координатой z составим уравнение изогнутой оси балки. Поскольку распределенная нагрузка q прерывается, ее необходимо продолжить до конца балки, одновременно добавив такую же нагрузку по модулю, но противоположно направленную. Поскольку 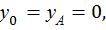 имеем:
имеем:
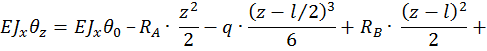
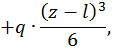
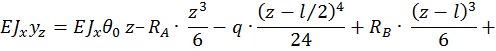
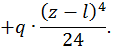
Для определения 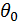 используем условие, что при z = l ,
используем условие, что при z = l , 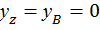 , тогда угол поворота
, тогда угол поворота 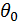 равен
равен
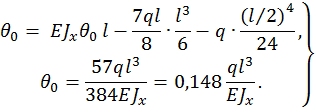
Угол поворота 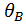 находим, подставляя z = l , тогда:
находим, подставляя z = l , тогда:
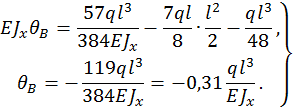
Находим прогиб в сечении D, для этого подставляем 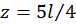 :
:
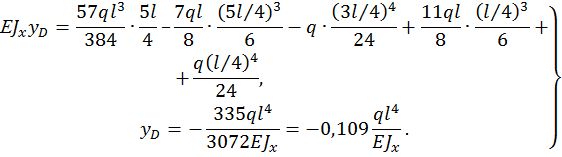
МЕТОД МОРА
Основные положения
В данном разделе рассмотрим общий метод определения перемещений (линейных и угловых), возникающих при прямом поперечном изгибе плоских стержневых систем, когда их оси могут быть не только прямыми, но и иметь некоторую малую кривизну и состоять из нескольких участков, имеющих непостоянную жесткость, то есть 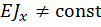 .
.
Наиболее просто эти уравнения находятся с помощью энергетических соотношений, полученных на основе общего выражения потенциальной энергии и равенства 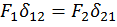 , представляющего собой теорему о взаимности работ и перемещений (теорему Бетти). Работа первой силы
, представляющего собой теорему о взаимности работ и перемещений (теорему Бетти). Работа первой силы 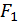 на перемещении точки её приложения
на перемещении точки её приложения 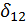 под действием второй силы
под действием второй силы 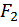 равна работе второй силы
равна работе второй силы 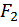 на перемещении точки её приложения
на перемещении точки её приложения 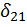 под действием первой силы
под действием первой силы 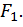 В частном случае при
В частном случае при 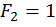 можно записать
можно записать 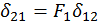 . Но
. Но 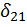 – это перемещение сечения 2 под действием некоторой обобщенной силы
– это перемещение сечения 2 под действием некоторой обобщенной силы 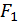 .
.
Отсюда вытекает очень важный вывод, что если требуется определить перемещение в каком либо сечении, то в этом сечении по направлению перемещения необходимо приложить нагрузку, равную единице: 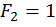 . Выражая работу
. Выражая работу 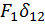 через внутренние усилия в поперечном сечении стержня в единичном и грузовом состоянии, можно получить выражение для определения перемещения
через внутренние усилия в поперечном сечении стержня в единичном и грузовом состоянии, можно получить выражение для определения перемещения 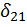 :
:
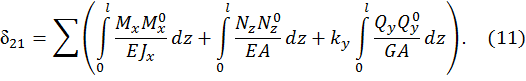
Данное выражение носит название формулы Максвелла – Мора (чаще используется одна фамилия Мора). В этой формуле 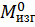 ,
, 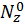 ,
, 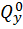 – внутренние усилия, возникающие в поперечном сечении стержня, вызванные действием единичной силы
– внутренние усилия, возникающие в поперечном сечении стержня, вызванные действием единичной силы 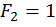 или единичного момента
или единичного момента 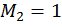 , прикладываемых по направлению искомого перемещения. В первом случае перемещение
, прикладываемых по направлению искомого перемещения. В первом случае перемещение 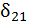 является линейным, во втором – угловым.
является линейным, во втором – угловым.
Однако в большинстве случаев при изгибе влиянием продольных деформаций и деформаций сдвига от 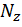 и
и 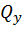 соответственно можно пренебречь и учитывать лишь перемещения, вызванные изгибом. Тогда формула Мора для плоской системы может быть записана следующим образом:
соответственно можно пренебречь и учитывать лишь перемещения, вызванные изгибом. Тогда формула Мора для плоской системы может быть записана следующим образом:
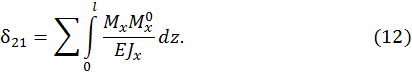
2.2. Порядок определения перемещений по методу Мора
1. Для каждого участка балки (плоской стержневой системы) составляется выражение изгибающего момента 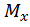 в произвольном сечении от действия внешней нагрузки.
в произвольном сечении от действия внешней нагрузки.
2. Строится вспомогательная балка (стержневая система) и нагружается единичной нагрузкой в точке, где требуется определить перемещение. При определении линейного перемещения в заданном направлении прикладывается единичная сила, при определении углового перемещения – единичный момент. Затем для каждого участка записывается выражение изгибающего момента  от единичной нагрузки.
от единичной нагрузки.
3. Записывается и вычисляется для каждого участка интеграл Мора. При этом если направление единичной нагрузки совпадает с направлением перемещения сечения, то получается положительный знак. Отрицательный знак свидетельствует, что направление перемещения сечения происходит в сторону, противоположную направлению единичной нагрузки.
2.3. Примеры определения перемещений по методу Мора
Пример 1. Определить способом Максвелла-Мора вертикальный прогиб и угол поворота сечения С (рис. 5) при известных F , a , E , 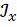 .
.
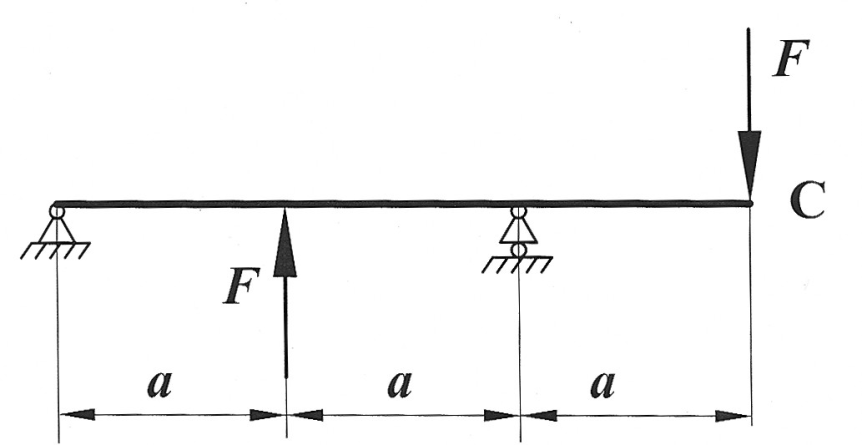
Рис. 5
Решение.
Перемещения сечений балки (прогиб и угол поворота) по методу Максвелла-Мора вычисляется по следующей формуле:
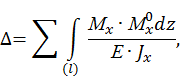
где 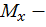 изгибающий момент в текущем сечении балки от внешней нагрузки,
изгибающий момент в текущем сечении балки от внешней нагрузки, 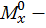 изгибающий момент в том же сечении от единичной нагрузки.
изгибающий момент в том же сечении от единичной нагрузки.
Определим реакции опор RА и RВ, запишем выражения для определения изгибающего момента в сечении z на каждом участке от внешней нагрузки. Построим эпюры изгибающего момента 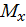 от внешней нагрузки (грузовую эпюру, рис. 6, б):
от внешней нагрузки (грузовую эпюру, рис. 6, б):
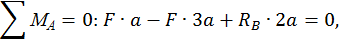
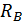 =
= 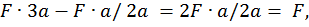
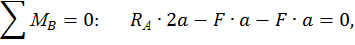
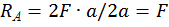 .
.
Проверка:
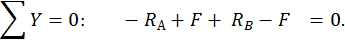
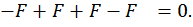
Строим эпюры 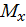 :
:
Первый участок: 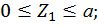
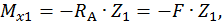
при  :
:
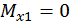 ,
,
при 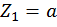 :
:
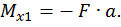
Второй участок: 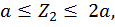
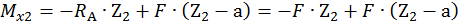 ,
,
при 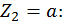
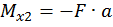
при 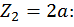
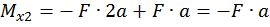 .
.
Третий участок: 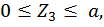
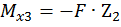 ,
,
при 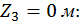
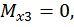
при 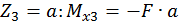 .
.
При отыскании прогиба за единичную силу принимается груз 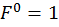 , приложенный в том сечении, где отыскивается прогиб, то есть в сечении С (рис. 6, в).
, приложенный в том сечении, где отыскивается прогиб, то есть в сечении С (рис. 6, в).
Определим реакции опор RА и RВ, запишем выражения для определения изгибающего момента в сечении z на каждом участке от единичной силы 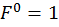 . Построим эпюры изгибающего момента
. Построим эпюры изгибающего момента  от единичной нагрузки (единичную эпюру, рис. 6, г):
от единичной нагрузки (единичную эпюру, рис. 6, г):
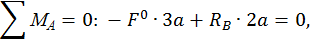
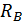 =
= 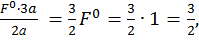
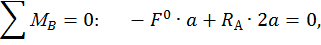
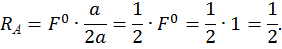
Проверка:
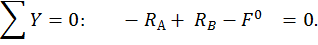
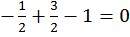 .
.
Строим эпюры  :
:
Первый участок: 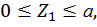
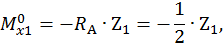
при  :
:
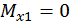 ,
,
при 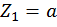 :
:
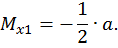
Второй участок: 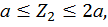
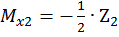 ,
,
при 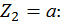
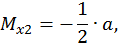
при 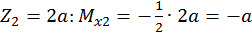 .
.
Третий участок: 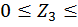 а,
а,
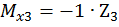 ,
,
при 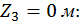
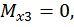
при 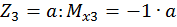 .
.
По методу Максвелла-Мора вычисляем прогиб как сумму трех интегралов:
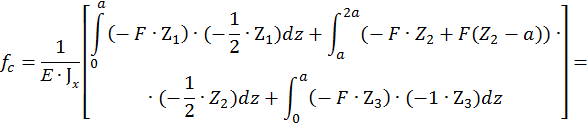
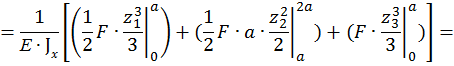
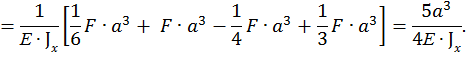
Знак «+» в ответе показывает, что прогиб направлен в ту же сторону, что и сила 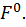
При отыскании угла поворота в том сечении, где определяется угол поворота, то есть в сечении С, прикладывается 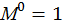 (рис. 6, д).
(рис. 6, д).
Определим реакции опор RА и RВ, запишем выражения для определения изгибающего момента в сечении z на каждом участке от единичного момента 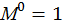 . Построим эпюры изгибающего момента
. Построим эпюры изгибающего момента  от единичного момента (рис. 6, е):
от единичного момента (рис. 6, е):
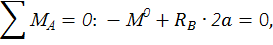
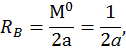
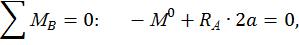
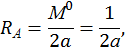
Проверка:
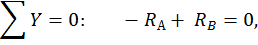
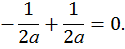
Строим эпюры  :
:
Первый участок: 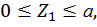
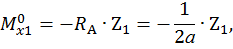
при  :
:
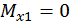 ,
,
при 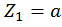 :
:
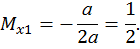
Второй участок: 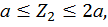
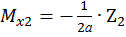 ,
,
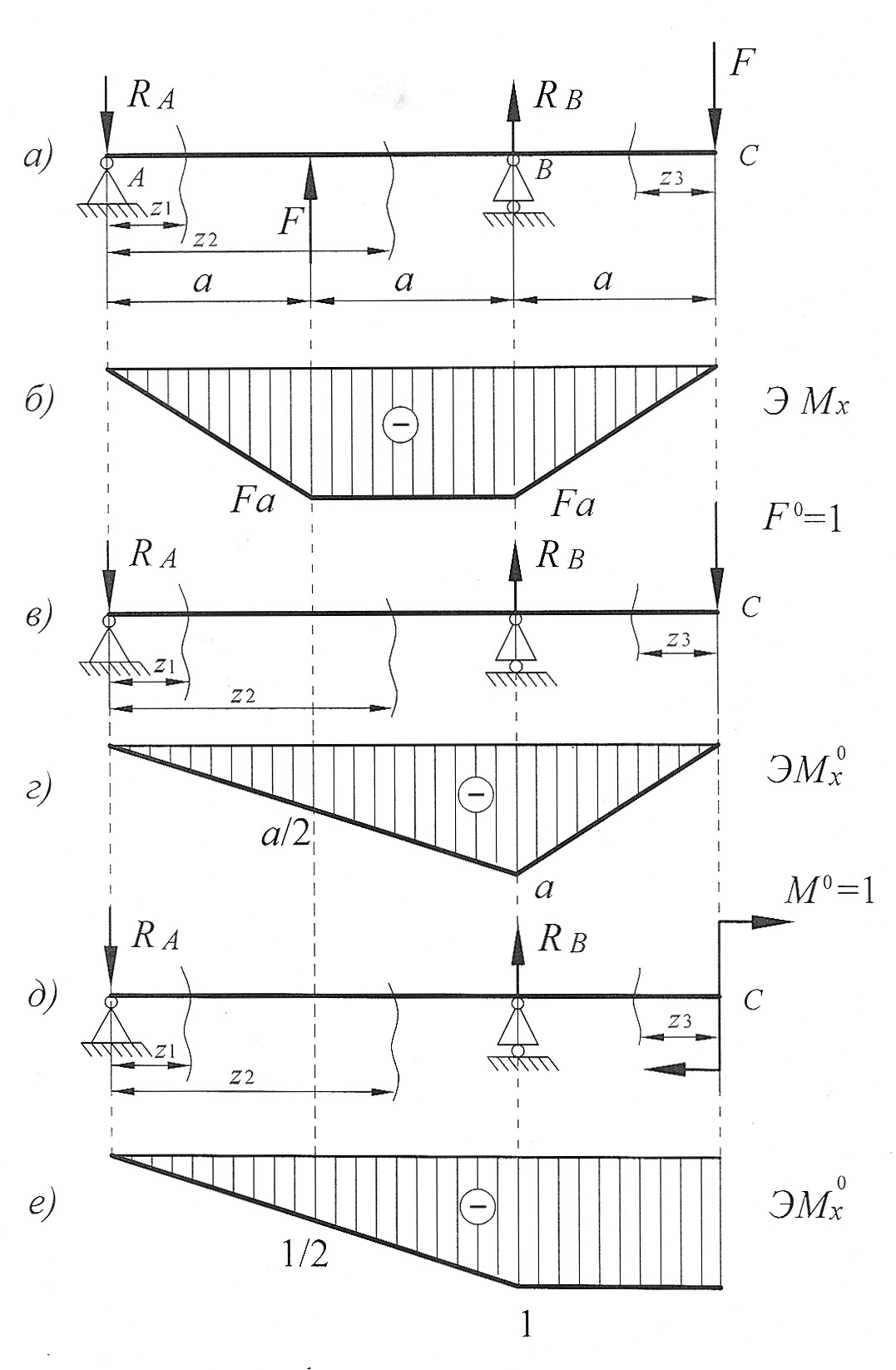
Рис. 6
при 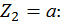
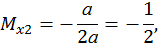
при 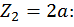
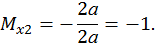
Третий участок: 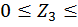 а,
а,
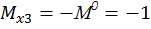 .
.
По методу Максвелла-Мора вычисляем прогиб как сумму трех интегралов:
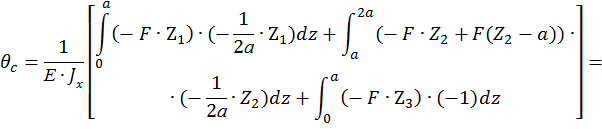
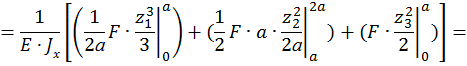
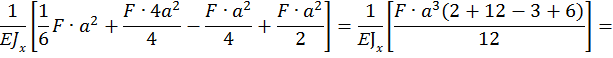
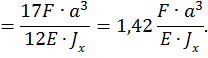
Знак «+» перед 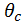 показывает, что направление поворота сечения совпадает с направлением единичного момента
показывает, что направление поворота сечения совпадает с направлением единичного момента 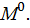
ПРАВИЛО ВЕРЕЩАГИНА
Основные положения
К основным недостаткам определения перемещения при помощи интеграла Мора можно отнести необходимость составления аналитического выражения подынтегральной функции и её интегрирование. Это особенно неудобно при определении перемещений в стержне, имеющем большое количество участков. Однако, если стержень состоит из прямых участков с постоянной в пределах каждого участка жесткостью 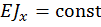 , то операцию интегрирования можно упростить. Эти упрощения основываются на том, что эпюры изгибающего момента от единичной нагрузки на прямых участках оказываются всегда линейными. А.К. Верещагин предложил для стержней с постоянной жесткостью и с прямолинейной в пределах каждого участка осью вместо непосредственного вычисления интеграла Мора графоаналитический прием его определения.
, то операцию интегрирования можно упростить. Эти упрощения основываются на том, что эпюры изгибающего момента от единичной нагрузки на прямых участках оказываются всегда линейными. А.К. Верещагин предложил для стержней с постоянной жесткостью и с прямолинейной в пределах каждого участка осью вместо непосредственного вычисления интеграла Мора графоаналитический прием его определения.
Рассмотрим, например, две эпюры изгибающих моментов, из которых одна  имеет произвольное очертание, а другая
имеет произвольное очертание, а другая  – прямолинейна (рис. 7).
– прямолинейна (рис. 7).
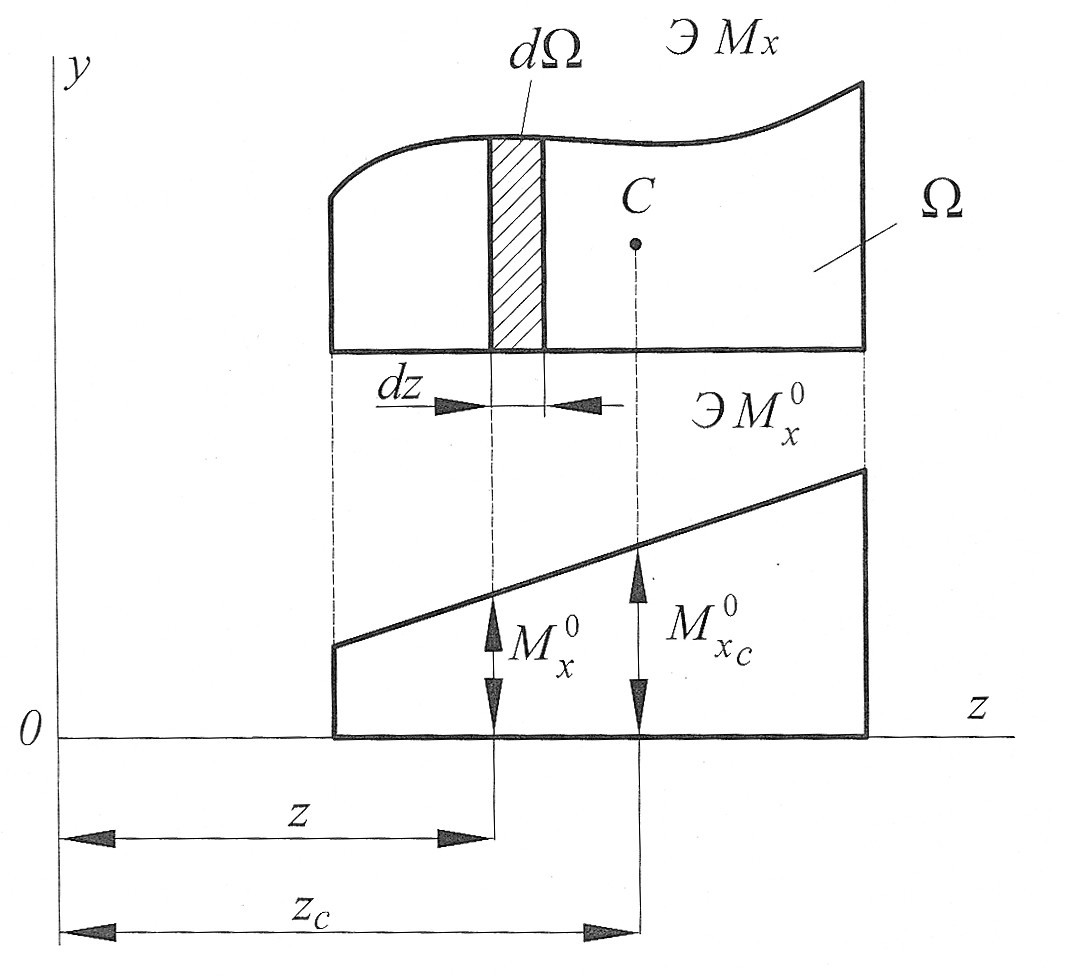
Рис. 7
В этом случае перемещение 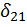 по правилу А.К. Верещагина может быть вычислено как
по правилу А.К. Верещагина может быть вычислено как
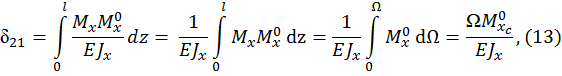
где 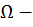 площадь эпюры, построенной от внешней нагрузки,
площадь эпюры, построенной от внешней нагрузки,
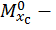 ордината эпюры изгибающих моментов, построенной от единичной нагрузки и расположенной под центром тяжести эпюры
ордината эпюры изгибающих моментов, построенной от единичной нагрузки и расположенной под центром тяжести эпюры 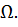
Практически искомое перемещение 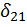 может быть вычислено как произведение площади эпюры изгибающего момента от внешней нагрузки
может быть вычислено как произведение площади эпюры изгибающего момента от внешней нагрузки 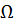 на значение изгибающего момента
на значение изгибающего момента 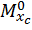 от единичной нагрузки, расположенного под центром тяжести грузовой эпюры
от единичной нагрузки, расположенного под центром тяжести грузовой эпюры 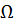 .
.
Участки по изгибающему моменту следует различать не только по нагрузке, но и по жесткости поперечного сечения. Если эпюры  и
и  расположены по одну сторону от стержня, то произведение
расположены по одну сторону от стержня, то произведение 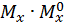 положительно. Если обе эпюры прямолинейны, то безразлично, для какой из них находить площадь
положительно. Если обе эпюры прямолинейны, то безразлично, для какой из них находить площадь 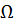 или значение
или значение  . Если эпюра
. Если эпюра  имеет сложное очертание, то ее следует разбить на части, для которых просто определяется площадь
имеет сложное очертание, то ее следует разбить на части, для которых просто определяется площадь 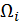 и центр тяжести
и центр тяжести 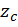 . Чаще всего элементами разбиения площади эпюры
. Чаще всего элементами разбиения площади эпюры 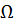 являются: треугольник, прямоугольник и фигуры, очерченные квадратичными параболами (в случае действия равномерно распределенной нагрузки). Сведения о площадях и координатах центра тяжести простых эпюр (фигур) приведены в таблице 1.
являются: треугольник, прямоугольник и фигуры, очерченные квадратичными параболами (в случае действия равномерно распределенной нагрузки). Сведения о площадях и координатах центра тяжести простых эпюр (фигур) приведены в таблице 1.
Таблица 1. Значения площадей некоторых простейших эпюр
Примеры разбиения сложных площадей эпюр
Изгибающих моментов
Пример 1. Предположим, что эпюры изгибающих моментов, построенные от внешней нагрузки, представляют собой однозначную трапецию (рис. 8).
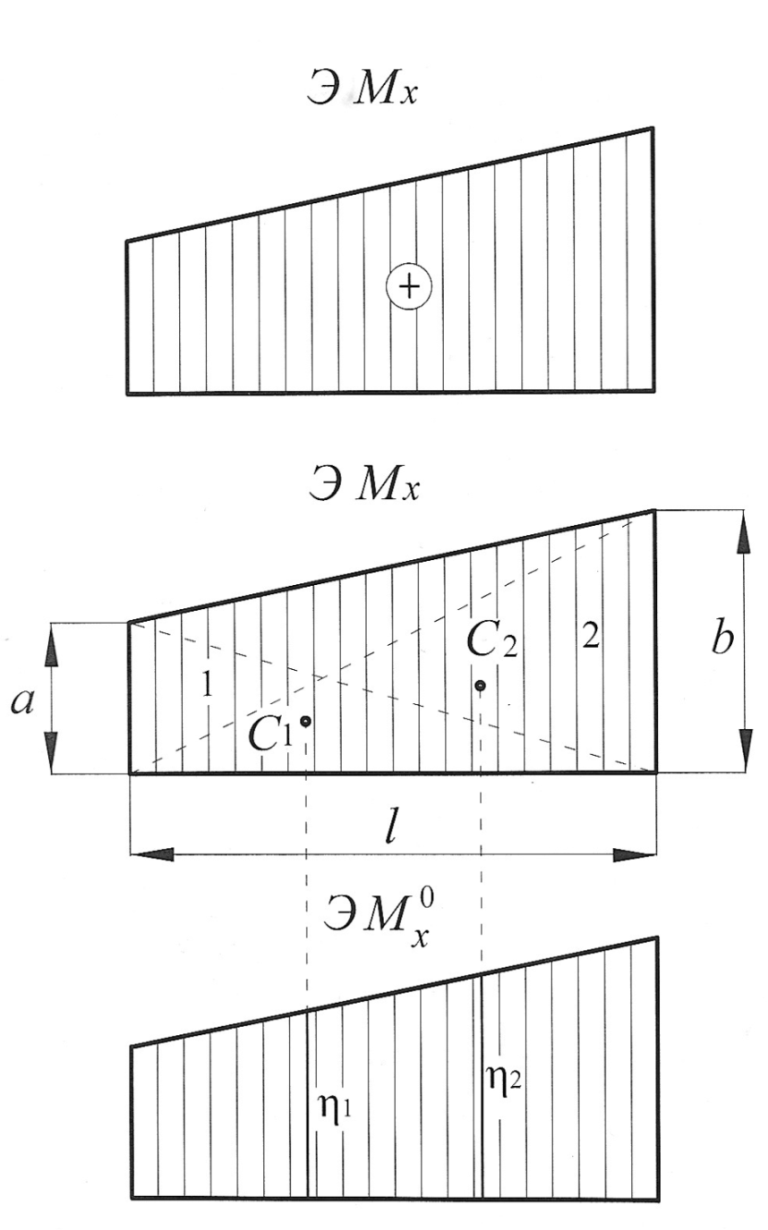
Рис. 8
Разбиваем эпюру  на два однозначных треугольника с площадями
на два однозначных треугольника с площадями 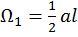 ,
, 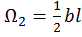 . Обозначим значения единичных моментов под центрами тяжести треугольников как
. Обозначим значения единичных моментов под центрами тяжести треугольников как 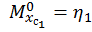 и
и 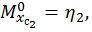 тогда
тогда
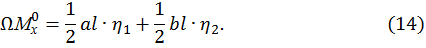
Пример 2. Эпюра от внешней нагрузки представляет собой разнозначную трапецию (рис. 9).
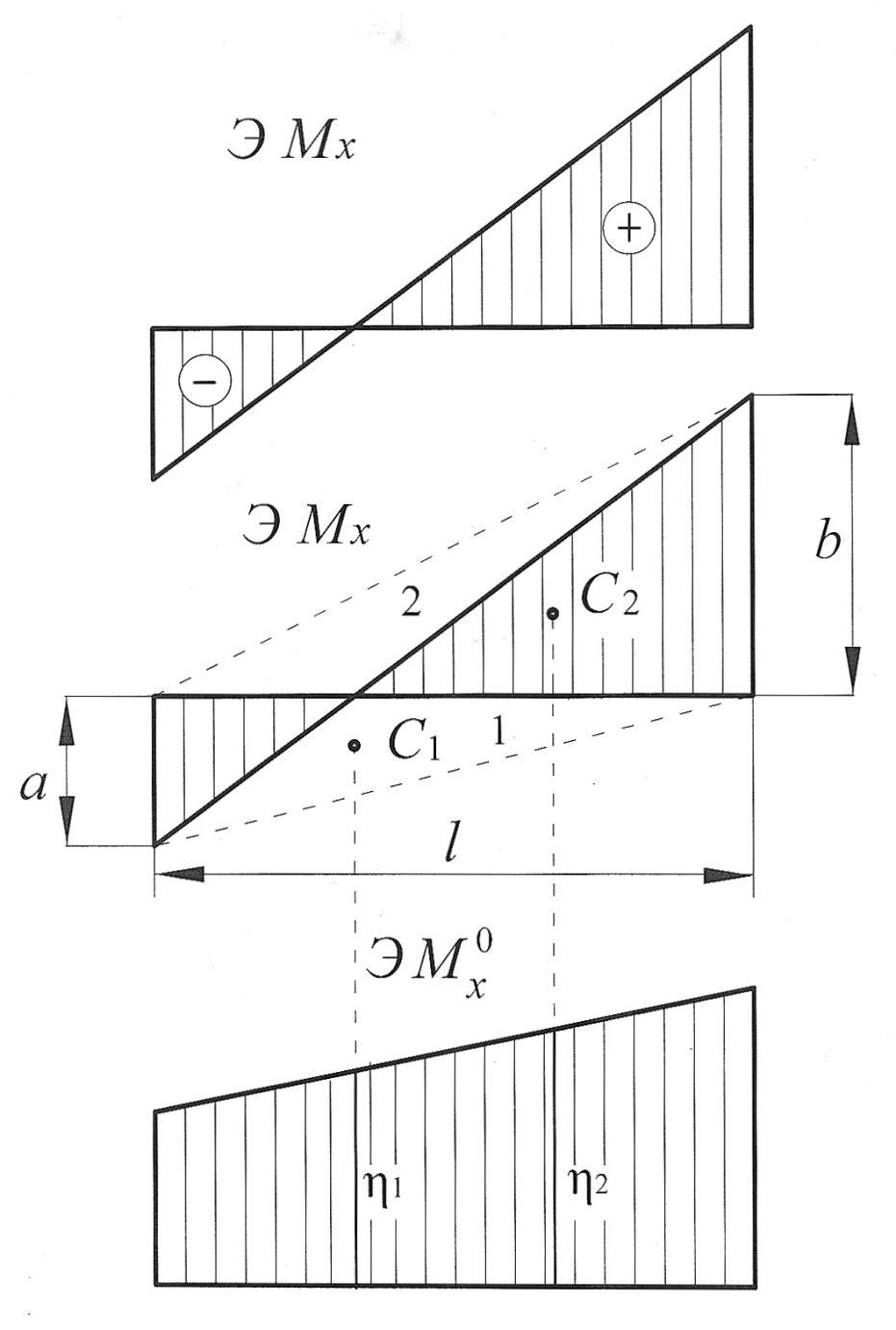
Рис. 9
Разбиваем эпюру 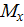 на два разнозначных треугольника. Один треугольник (1) расположен снизу от оси z, второй треугольник (2) расположен сверху от оси z. Произведение
на два разнозначных треугольника. Один треугольник (1) расположен снизу от оси z, второй треугольник (2) расположен сверху от оси z. Произведение 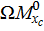 имеет знак минус, если эпюры
имеет знак минус, если эпюры 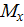 и
и 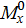 расположены по разные стороны от оси z, и наоборот,
расположены по разные стороны от оси z, и наоборот, 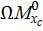 имеет знак плюс, если эпюры
имеет знак плюс, если эпюры 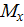 и
и 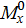 расположены по одну сторону от оси z , тогда
расположены по одну сторону от оси z , тогда
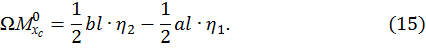
Пример 3. Эпюра 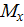 от внешней нагрузки (грузовая эпюра) представляет собой однозначную трапецию, ограниченную сверху параболой (рис. 10).
от внешней нагрузки (грузовая эпюра) представляет собой однозначную трапецию, ограниченную сверху параболой (рис. 10).
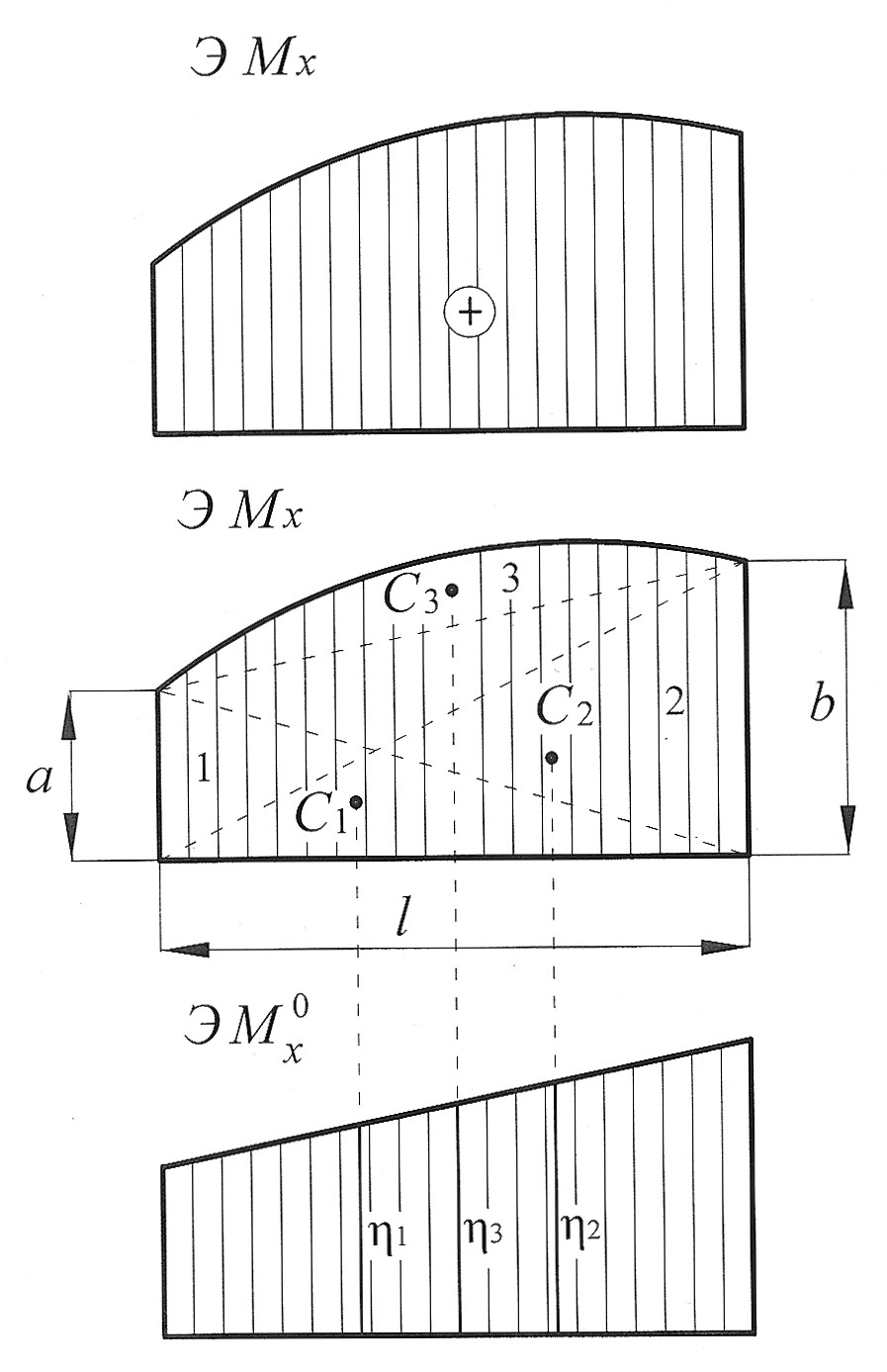
Рис. 10
Разбиваем эпюру 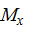 на два однозначных треугольника и квадратичную параболу с нулевыми начальным и конечным значениями c площадью
на два однозначных треугольника и квадратичную параболу с нулевыми начальным и конечным значениями c площадью 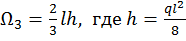 , и с центром тяжести
, и с центром тяжести 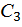 , который находится на середине длины l, тогда
, который находится на середине длины l, тогда
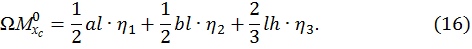
Пример 4. Эпюра 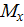 от внешней нагрузки (грузовая эпюра) представляет собой разнозначную трапецию, ограниченную сверху параболой (рис. 11).
от внешней нагрузки (грузовая эпюра) представляет собой разнозначную трапецию, ограниченную сверху параболой (рис. 11).
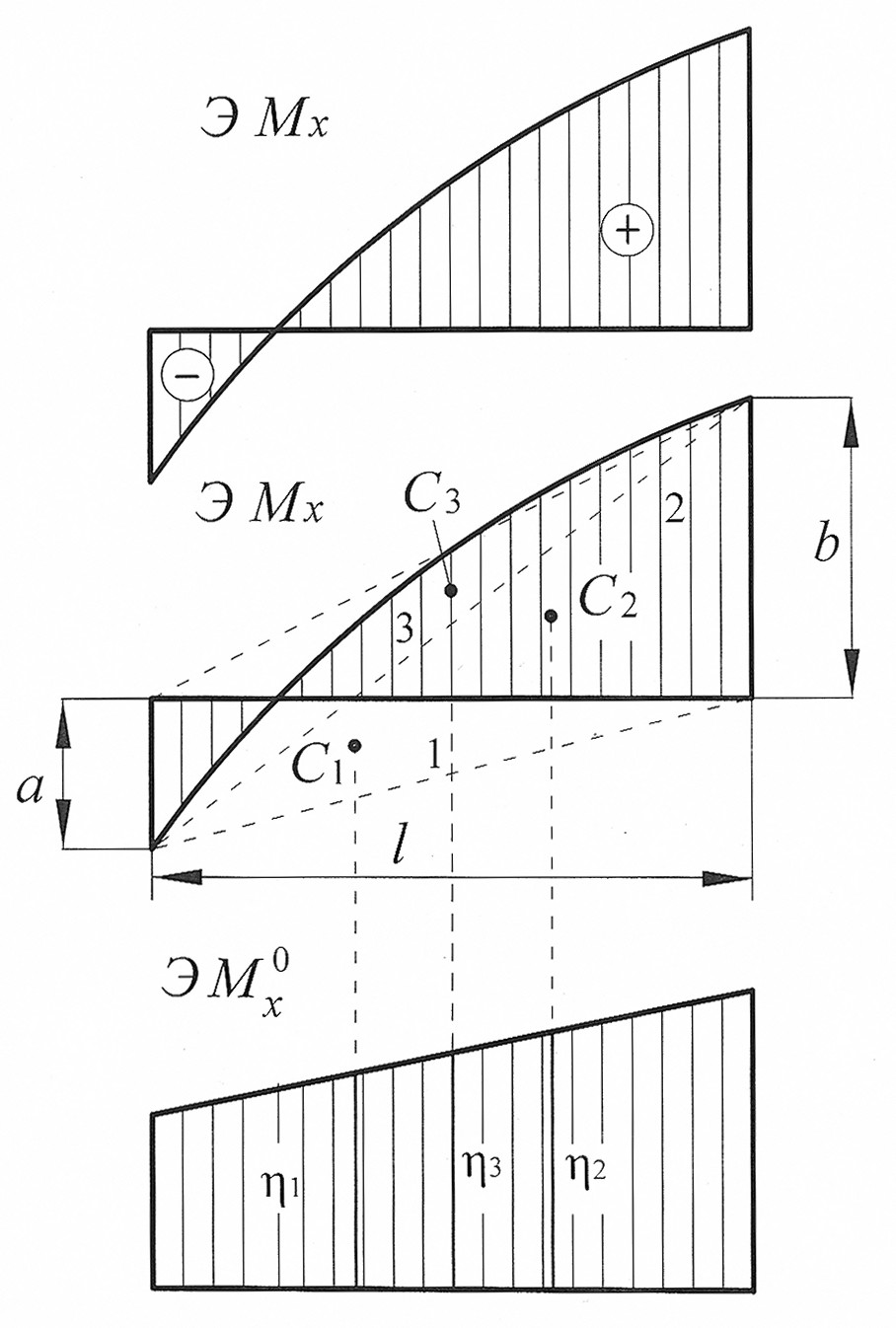
Рис. 11
Разбиваем эпюру 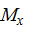 на два разнозначных треугольника и квадратичную параболу с нулевыми начальным и конечным значениями с площадью
на два разнозначных треугольника и квадратичную параболу с нулевыми начальным и конечным значениями с площадью 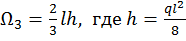 , и с центром тяжести
, и с центром тяжести 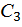 , который находится на середине длины l, тогда
, который находится на середине длины l, тогда
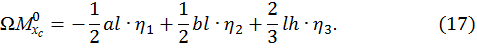
Пример 5. Предположим, эпюра 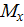 , построенная от внешней нагрузки (грузовая эпюра), представляет собой треугольник, ограниченный сверху выпуклой параболой. Такая эпюра получается, например, если консольная балка нагружена на свободном конце сосредоточенной силой, направленной вверх, и распределенной нагрузкой, направленной вниз (рис. 12).
, построенная от внешней нагрузки (грузовая эпюра), представляет собой треугольник, ограниченный сверху выпуклой параболой. Такая эпюра получается, например, если консольная балка нагружена на свободном конце сосредоточенной силой, направленной вверх, и распределенной нагрузкой, направленной вниз (рис. 12).
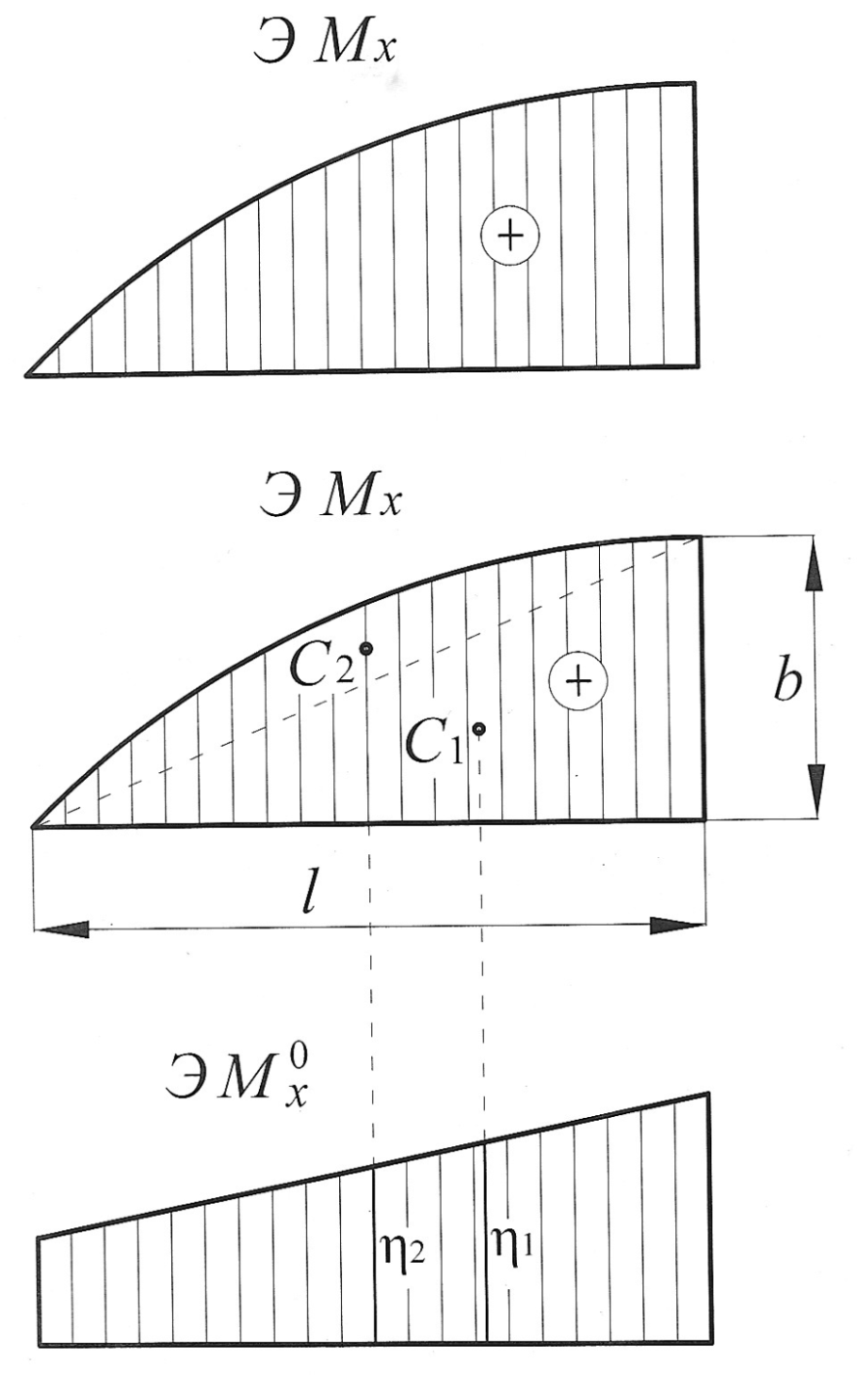
Рис. 12
Разбиваем эпюру 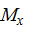 на треугольник с площадью
на треугольник с площадью 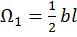 и центром тяжести
и центром тяжести 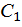 и квадратичную параболу с нулевыми начальным и конечным значениями с площадью
и квадратичную параболу с нулевыми начальным и конечным значениями с площадью 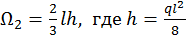 , и центром тяжести
, и центром тяжести 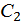 , тогда
, тогда
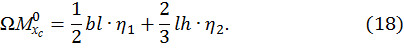
Пример 6. Предположим, эпюра 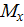 , построенная от внешней нагрузки (грузовая эпюра), представляет собой треугольник, ограниченный сверху вогнутой параболой. Такая эпюра получается, например, если консольная балка нагружена на свободном конце сосредоточенной силой и распределенной нагрузкой, которые направлены вверх (рис. 13).
, построенная от внешней нагрузки (грузовая эпюра), представляет собой треугольник, ограниченный сверху вогнутой параболой. Такая эпюра получается, например, если консольная балка нагружена на свободном конце сосредоточенной силой и распределенной нагрузкой, которые направлены вверх (рис. 13).
Рис. 13
Разбиваем эпюру 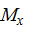 на треугольник с площадью
на треугольник с площадью 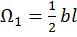 и с центром тяжести
и с центром тяжести 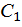 и квадратичную параболу с нулевыми начальным и конечным значениями с площадью
и квадратичную параболу с нулевыми начальным и конечным значениями с площадью 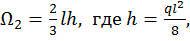 и центром тяжести
и центром тяжести 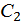 , тогда
, тогда
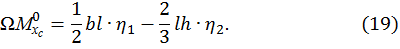
3.4. Пример определения перемещений по способу Верещагина
Пример 1. Определить способом Верещагина величину вертикального перемещения и угол поворота свободного конца консольной двутавровой балки № 24 (рис. 14).
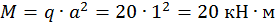 ,
, 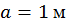 ,
, 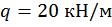 ,
,
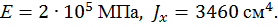
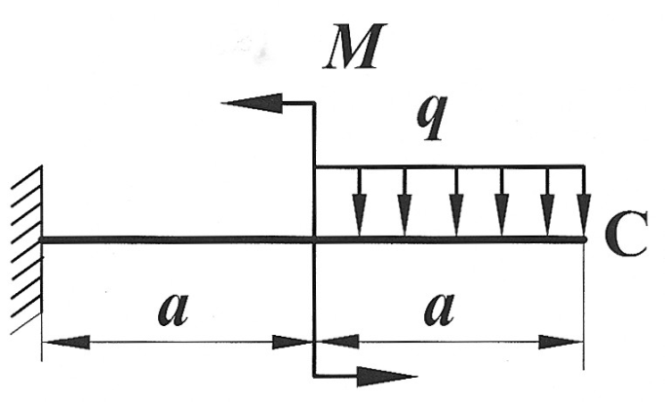
Рис. 14
Решение.
Любые перемещения  при нескольких прямолинейных участках нагружения балки вычисляются по правилу Верещагина по следующей формуле:
при нескольких прямолинейных участках нагружения балки вычисляются по правилу Верещагина по следующей формуле:
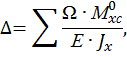
где 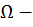 площадь эпюры изгибающего момента от заданной нагрузки,
площадь эпюры изгибающего момента от заданной нагрузки,
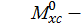 ордината эпюры изгибающего момента от единичной нагрузки.
ордината эпюры изгибающего момента от единичной нагрузки.
Ордината 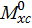 берется в том сечении участка балки, напротив которого находится центр тяжести эпюры изгибающего момента от заданной нагрузки на этом участке.
берется в том сечении участка балки, напротив которого находится центр тяжести эпюры изгибающего момента от заданной нагрузки на этом участке.
Построим эпюры изгибающего момента 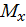 от внешней нагрузки (рис. 15, б):
от внешней нагрузки (рис. 15, б):
Первый участок: 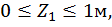
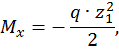
при  :
:
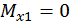 ,
,
при 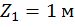 :
:
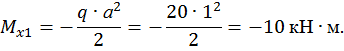
Второй участок: 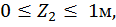
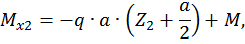
при 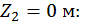
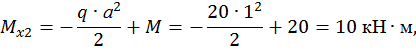
при 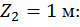
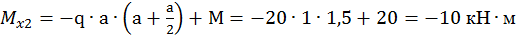 .
.
Для определения вертикального перемещения свободного конца консольной балки необходимо в этом сечении приложить силу 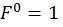 (рис. 15, в) и построить от этой силы единичную эпюру изгибающего момента
(рис. 15, в) и построить от этой силы единичную эпюру изгибающего момента 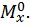
Построим эпюры изгибающего момента  (единичную эпюру рис. 15, г):
(единичную эпюру рис. 15, г):
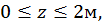
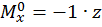 ,
,
при 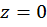 :
:
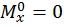 ,
,
при 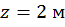 :
:
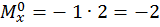 .
.
Эпюру изгибающего момента от заданной внешней нагрузки (грузовую эпюру) разбиваем на простые фигуры, образованные квадратичной параболой и двумя треугольниками, один сверху, а второй снизу от оси z (см. рис. 15, б).
Определим площади этих фигур 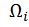 и
и 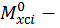 ординаты эпюры изгибающего момента от единичной нагрузки под центром тяжести эпюры изгибающего момента от заданной нагрузки на каждом участке (см. рис. 15, б, г):
ординаты эпюры изгибающего момента от единичной нагрузки под центром тяжести эпюры изгибающего момента от заданной нагрузки на каждом участке (см. рис. 15, б, г):
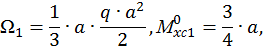
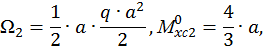
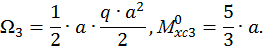
Если эпюры грузовая и единичная построены по одну сторону от оси z, то произведение 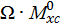 имеет знак «+», и наоборот – «-». Отсюда следует, что на втором участке
имеет знак «+», и наоборот – «-». Отсюда следует, что на втором участке 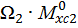 имеет знак «-».
имеет знак «-».
Определяем прогиб свободного конца балки:
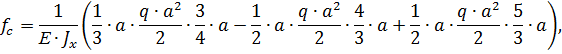
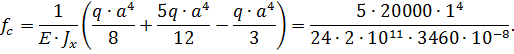
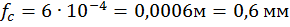 .
.
Прогиб 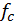 получился со знаком «+», это значит, что его направление соответствует направлению единичной силы.
получился со знаком «+», это значит, что его направление соответствует направлению единичной силы.
Для определения вертикального угла поворота свободного конца консольной балки необходимо в этом сечении приложить момент 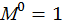 (рис. 15, д) и построить от этого момента единичную эпюру изгибающего момента
(рис. 15, д) и построить от этого момента единичную эпюру изгибающего момента 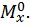
Построим от 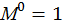 эпюры изгибающего момента
эпюры изгибающего момента  (единичную эпюру, рис. 15, е):
(единичную эпюру, рис. 15, е):
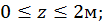
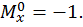
Так как площади грузовой эпюры на каждом участке уже найдены, то определим 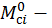 ординаты эпюры изгибающего момента от единичной нагрузки (единичного момента) под центром тяжести эпюры изгибающего момента от заданной нагрузки на каждом участке:
ординаты эпюры изгибающего момента от единичной нагрузки (единичного момента) под центром тяжести эпюры изгибающего момента от заданной нагрузки на каждом участке:
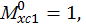
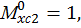
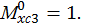
Определяем угол поворота балки со свободного конца:
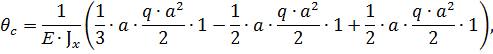
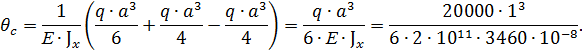
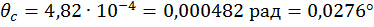
Значение угла поворота балки получилось со знаком «+», это значит, что балка поворачивается в том же направлении как действует единичный момент.
Ответ: 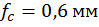 ,
, 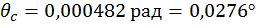 .
.
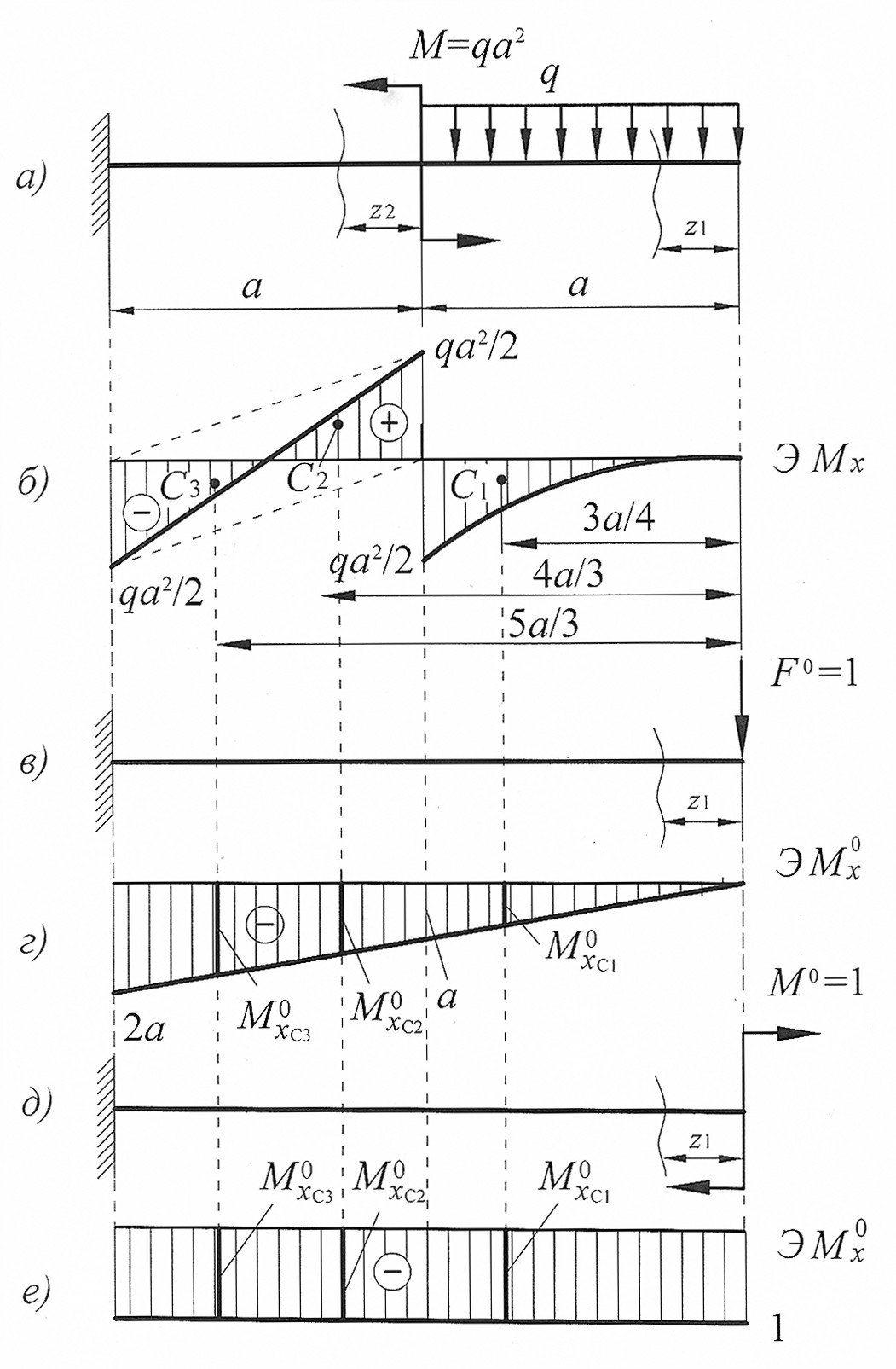
Рис. 15
ЗАДАЧИ ДЛЯ ПРОВЕРКИ СТУДЕНТАМИ СТЕПЕНИ УСВОЕНИЯ МАТЕРИАЛА РАЗДЕЛА «ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ПРИ ИЗГИБЕ»
Задача 1
По методу начальных параметров определить прогиб в сечении С и угол поворота в опоре А, если:
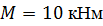 , , 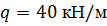 , ,
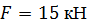 , , 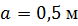 , ,
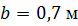 , , 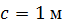 , ,
 , ,
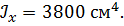
|
|
Задача 2
По методу начальных параметров определить прогиб в сечении С и угол поворота в опоре А, если:
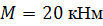 , , 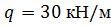 , ,
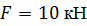 , , 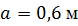 , ,
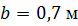 , , 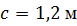 , ,
 , ,
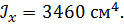
|
|
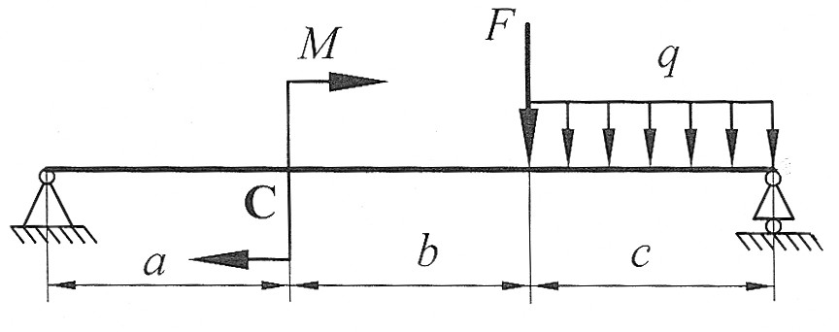
Задача 3
По методу начальных параметров определить прогиб и угол поворота в сечении С, если:
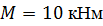 , , 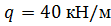 , ,
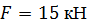 , , 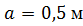 , ,
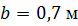 , , 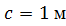 , ,
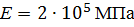 , ,
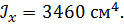
|
|
Задача 4
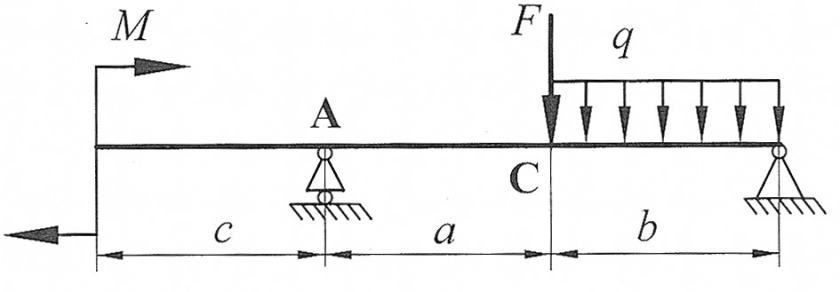
| По методу начальных параметров определить прогиб в сечении С и угол поворота в опоре А, если:
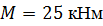 , ,
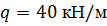 , ,
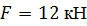 , , 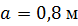 , ,
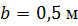 , , 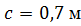 , ,
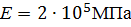 , , 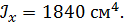
|
Задача 5
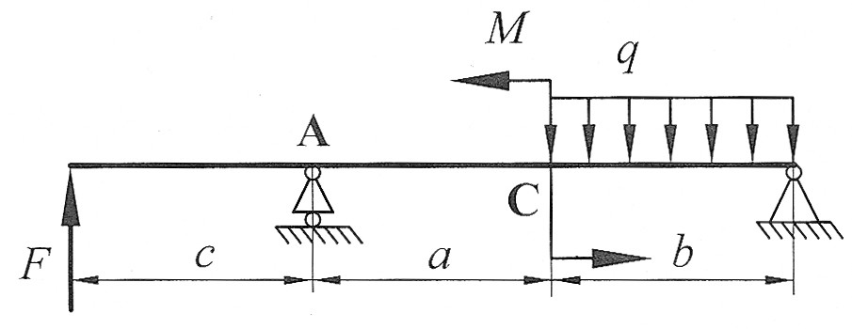
| По методу начальных параметров определить прогиб в сечении С и угол поворота в опоре А, если:
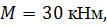
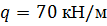 , ,
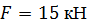 , , 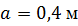 , ,
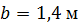 , , 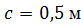 , ,
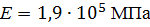 , , 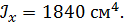
|
Задача 6
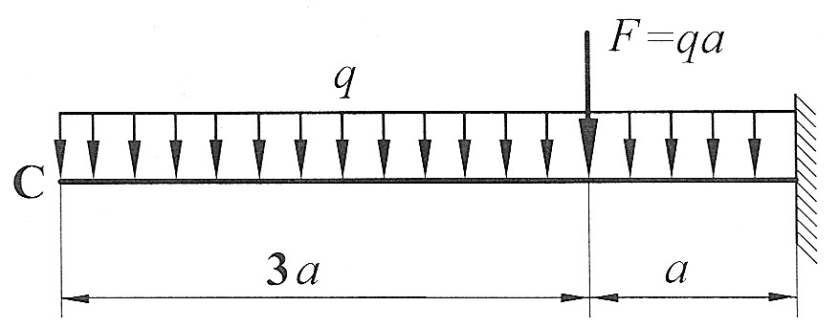
| По методу начальных параметров определить прогиб и угол поворота в сечении С, если:
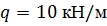 , ,
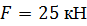 , , 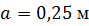 , ,
 , ,
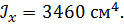
|
Задача 7
Определить способом Верещагина величину вертикального перемещения и угол поворота свободного конца консольной балки (сечения С).
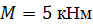 , ,
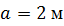 , ,
 , ,
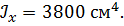
|

|
Задача 8
Определить способом Мора величину вертикального перемещения и угол поворота сечения С балки.
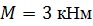 , ,
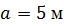 , ,

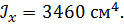
|
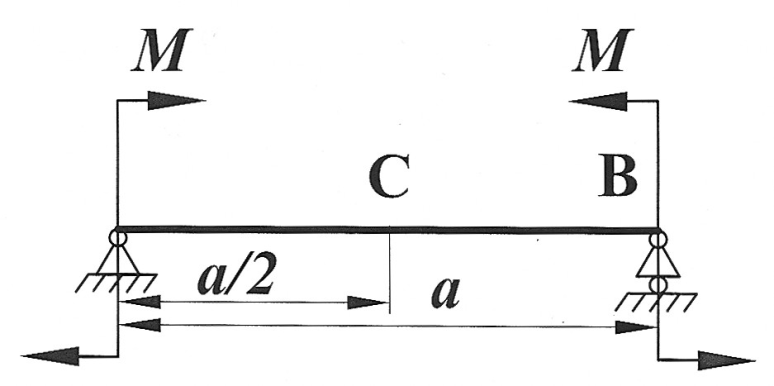
|
Задача 9
Определить способом Мора величину вертикального перемещения и угол поворота по середине пролета балки (сечения С).
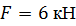 , ,
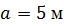 , ,
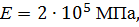
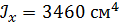 . .
|
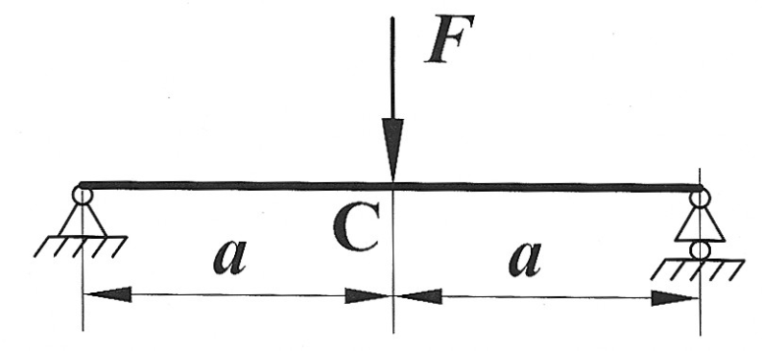
|
Задача 10
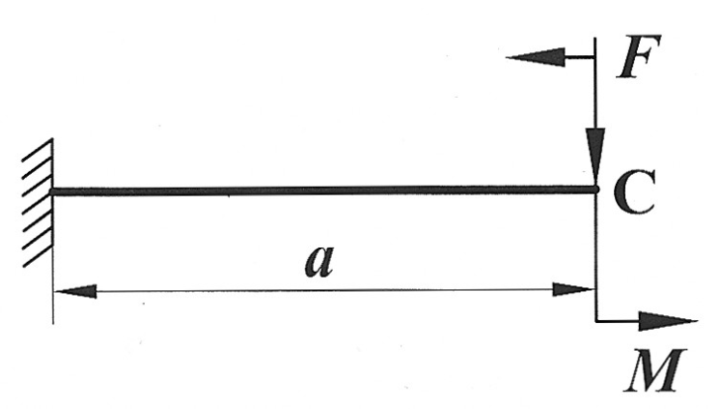
| Определить способом Мора величину вертикального перемещения и угол поворота свободного конца консольной балки (сечения С).
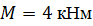 , ,
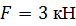
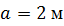 , ,
 , , 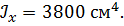
|
Задача 11
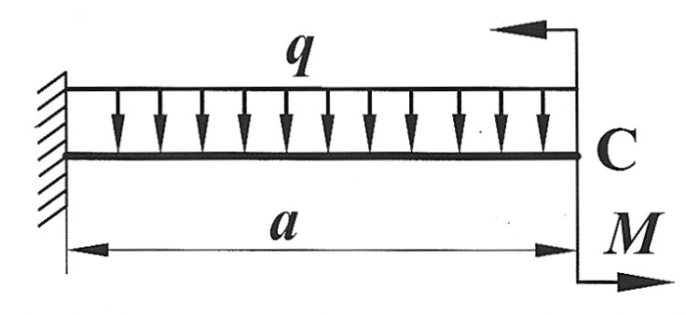
| Определить способом Мора величину вертикального перемещения и угол поворота свободного конца консольной балки (сечения С).
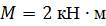 , ,
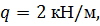
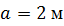 , ,
 , , 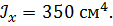
|
Задача 12
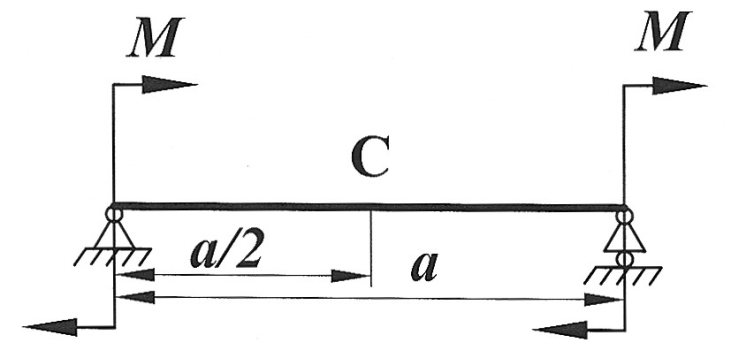
| Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С балки.
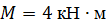 , ,
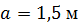 , ,
 , ,
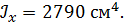
|
Задача 13
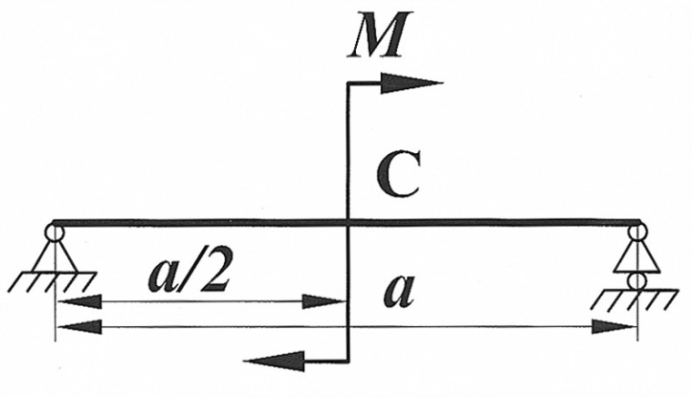
Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С стальной двутавровой балки № 27.
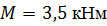 , ,
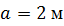 , ,
|
|
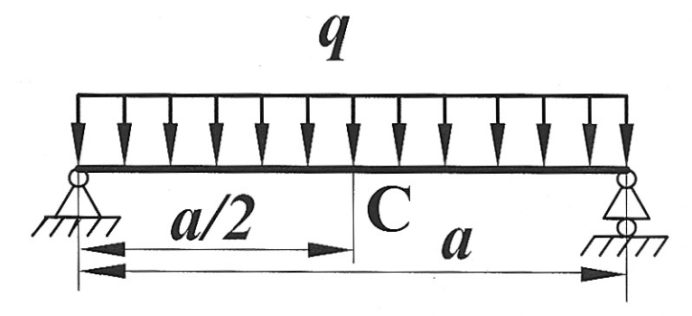
Задача 14
Определить способом Мора величину вертикального перемещения и угол поворота сечения С балки.
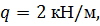
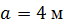 , ,
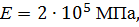
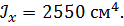
|
|
Задача 15
Определить способом Мора величину вертикального перемещения и угол поворота сечения С стальной двутавровой балки № 20.
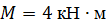 , ,
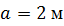 , ,
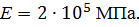
|
|
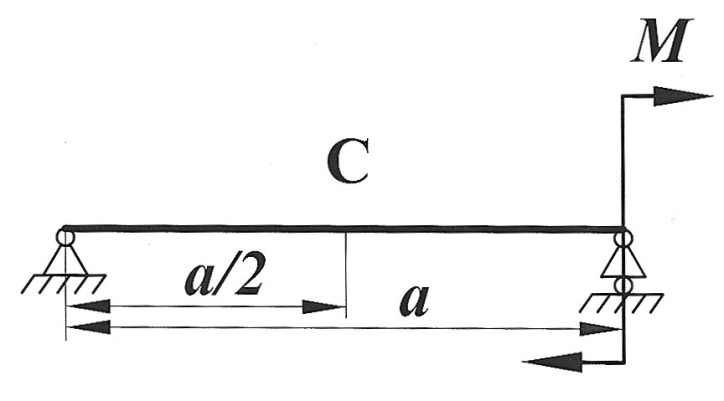
Задача 16
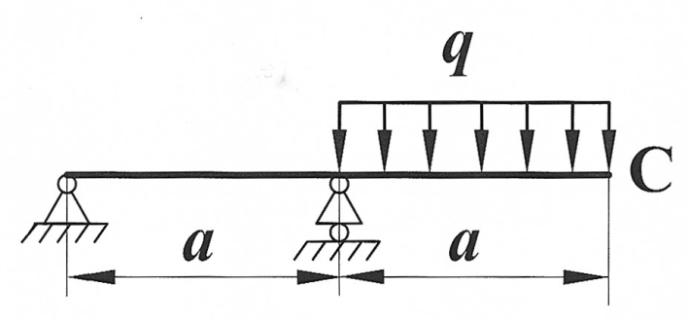
| Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С балки.
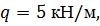
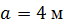 , ,
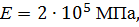
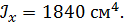
|
Задача 17
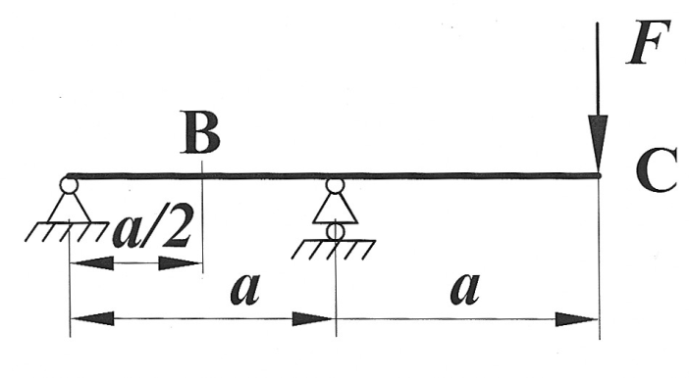
| Определить способом Верещагина величину вертикального перемещения сечения В и угол поворота сечения С балки.
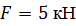 , ,
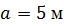 , ,
 , ,
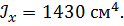
|
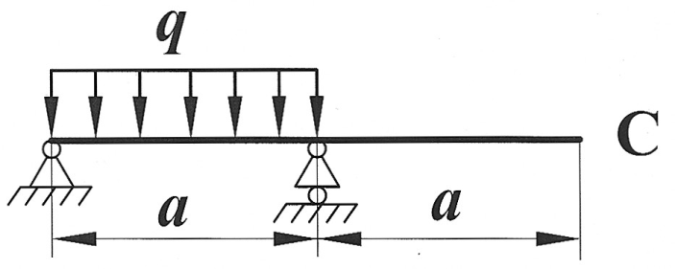
Задача 18
|
Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С стальной двутавровой балки
№ 20.
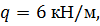
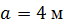 , ,
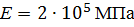
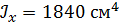 . .
|
Задача 19
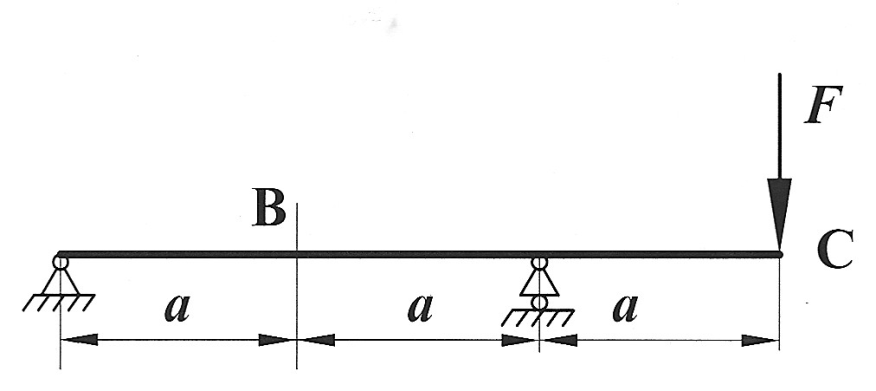
Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С балки.
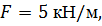
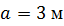 , ,
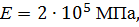
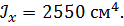
|
|
Задача 20
Определить способом Верещагина величину вертикального перемещения сечения В и угол поворота сечения С балки.
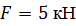 , ,
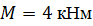 , ,

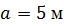 , ,
 , ,
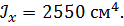
|
|
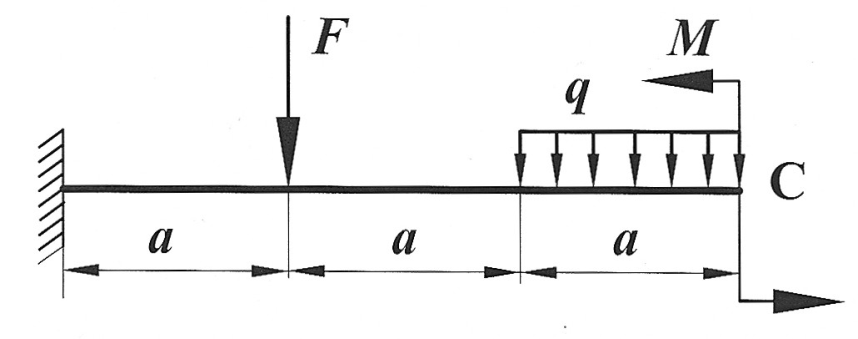
Задача 21
Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С стальной двутавровой балки № 20.
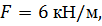
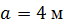 , ,
 , , 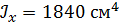 . .
|

|
Задача 22
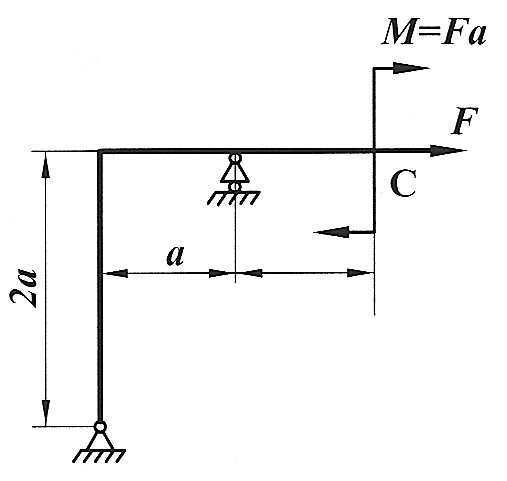
| Определить способом Верещагина величину вертикального, горизонтального перемещения и угол поворота сечения С статически определимой рамы.
F, a, E, 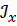 даны. даны.
|
Задача 23
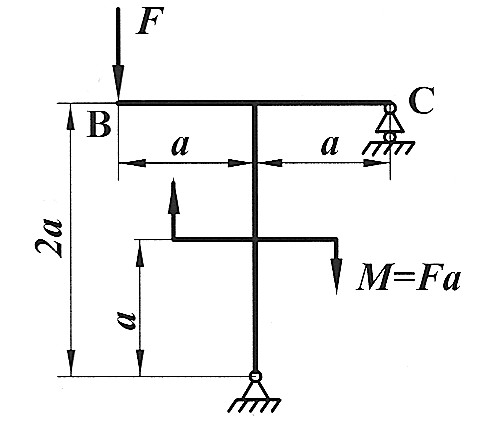
| Определить способом Верещагина величину вертикального перемещения сечения В и угол поворота сечения С статически определимой рамы.
F, a, E, 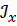 даны. даны.
|
Задача 24
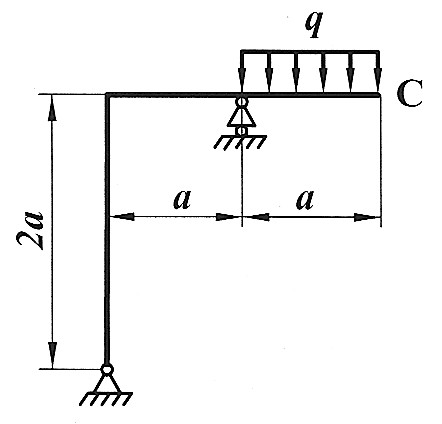
| Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С статически определимой рамы.
F, a, E, 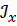 даны. даны.
|
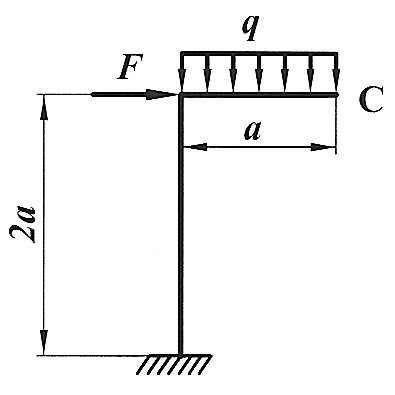
Задача 25
Определить способом Верещагина величину вертикального, горизонтального перемещения и угол поворота сечения С статически определимой рамы. F , a , E , 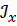 даны. даны.
| 
|
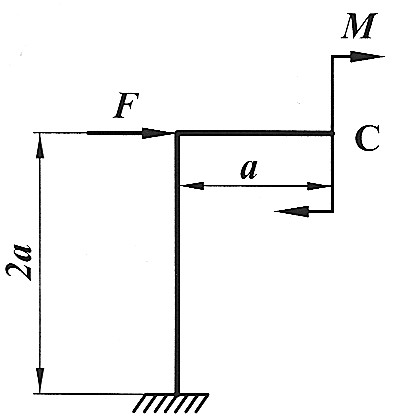
Задача 2 6
Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С статически определимой рамы.
F, a, E, 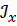 даны. даны.
| 
|
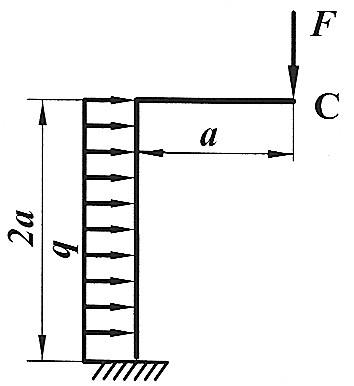
Задача 2 7
Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С статически определимой рамы. F , a , E , 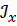 даны. даны.
| 
|
Задача 28
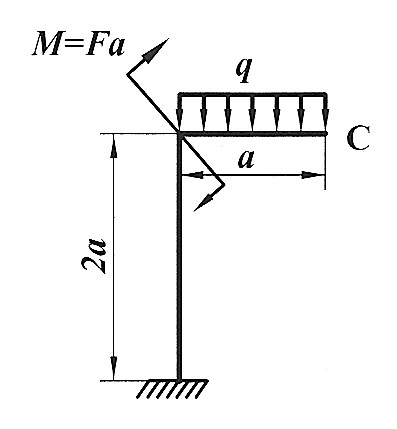
| Определить способом Верещагина величину вертикального, горизонтального перемещения и угол поворота сечения С статически определимой рамы. F, a, E, 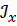 даны. даны.
|
Задача 2 9
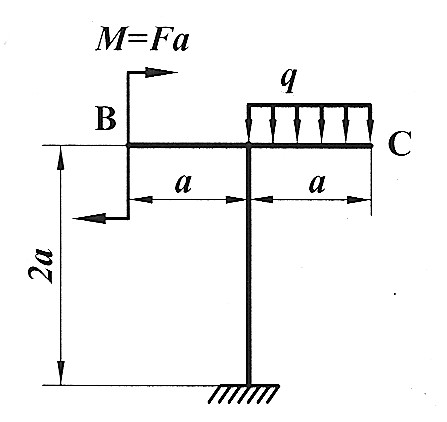
| Определить способом Верещагина величину вертикального перемещения сечения В и угол поворота сечения С статически определимой рамы. F , a , E , 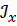 даны. даны.
|
Задача 30
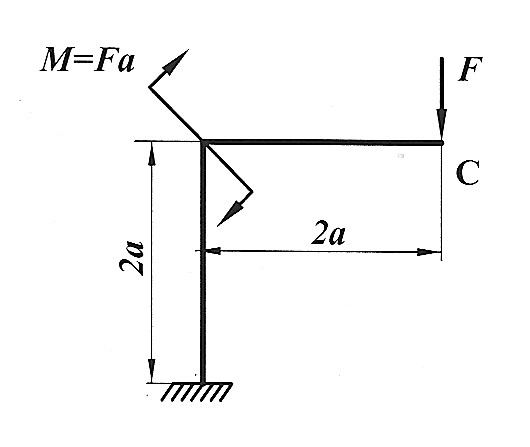
| Определить способом Верещагина величину вертикального перемещения и угол поворота сечения С статически определимой рамы. F , a , E , 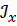 даны. даны.
|
Основные положения
Стержневые системы, в том числе и рамы, можно разделить на статически определимые и статически неопределимые. Любая стержневая система становится статически неопределимой, если на нее наложено связей больше, чем это необходимо для ее равновесия как жесткого целого.
Свободное тело в плоскости имеет три степени свободы. Чтобы тело находилось в равновесии, на него должны быть наложены три связи, называемые необходимыми. Связи, наложенные на тело сверх необходимых, называются дополнительными или «лишними». Число «лишних» связей, наложенных на систему, определяет ее степень статической неопределимости. Различают внешние и внутренние связи. Внешние связи накладывают в опорах системы и обеспечивают равновесие системы в целом. Внутренние связи обеспечивают равновесие любой произвольно выделенной части системы, то есть препятствуют взаимным перемещениям смежных сечений. В плоской раме в каждом сечении имеются три внутренние связи, препятствующие трем взаимным перемещениям: продольному, поперечному, угловому.
Усилия, возникающие во внешних связях, называются опорными реакциями, а во внутренних связях – внутренними силовыми факторами.
В статически определимых системах все реакции и внутренние силовые факторы определяются с помощью уравнений равновесия статики. В статически неопределимых системах для определения указанных величин недостаточно уравнений статики, необходимы еще дополнительные уравнения.
Расчет статически неопределимой рамы или балки начинается с определения степени статической неопределимости. Степень статической неопределимости k – это разность между числом неизвестных n (опорных реакций или внутренних силовых факторов) и числом независимых уравнений статики для заданной системы m:
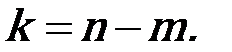
Для любой плоской системы число независимых уравнений статики равно 3.
Общим методом раскрытия статической неопределимости стержневых систем в машиностроении является метод сил. По методу сил расчет статически неопределимой системы заменяется расчетом основной системы, получаемой из заданной путем отбрасывания «лишних» связей. Реакции отброшенных связей заменяются неизвестными силами или моментами, обозначенными буквой Х. (Если связь препятствует линейному перемещению, она заменяется силой, угловому – моментом). Основная система – это статически определимая, кинематически неизменяемая система. Для статически неопределимой системы можно получить несколько основных систем в зависимости от удаленных связей.
В заданной системе перемещения по направлению отброшенных связей ограничены, в основной системе эти перемещения возможны. Для того чтобы основная система была эквивалентна заданной, необходимо, чтобы перемещения в основной системе по направлению отброшенных связей были соответственно равны перемещениям в заданной системе. Исходя из этого условия составляются дополнительные уравнения (уравнения перемещений). Если отбрасываемые связи жесткие, то перемещения по их направлению в заданной системе равны нулю, и дополнительные уравнения можно записать в таком виде:
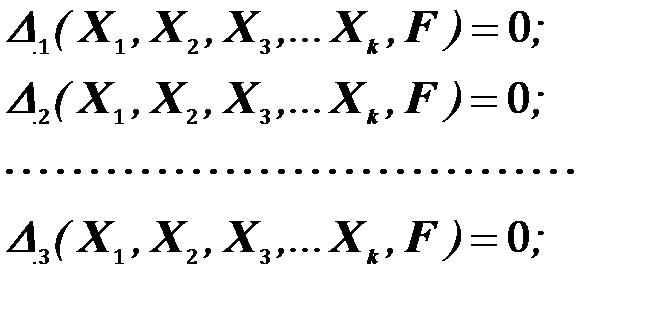 (20)
(20)
где 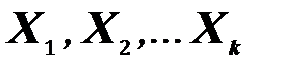 – реакции отброшенных связей;
– реакции отброшенных связей;
F – внешняя нагрузка в заданной системе;
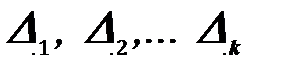 – перемещения в направлении отброшенных связей.
– перемещения в направлении отброшенных связей.
Пользуясь принципом независимости действия сил, перемещения 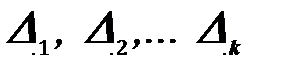 можно представить суммой перемещений от каждой нагрузки, и полученные выше уравнения принимают вид
можно представить суммой перемещений от каждой нагрузки, и полученные выше уравнения принимают вид


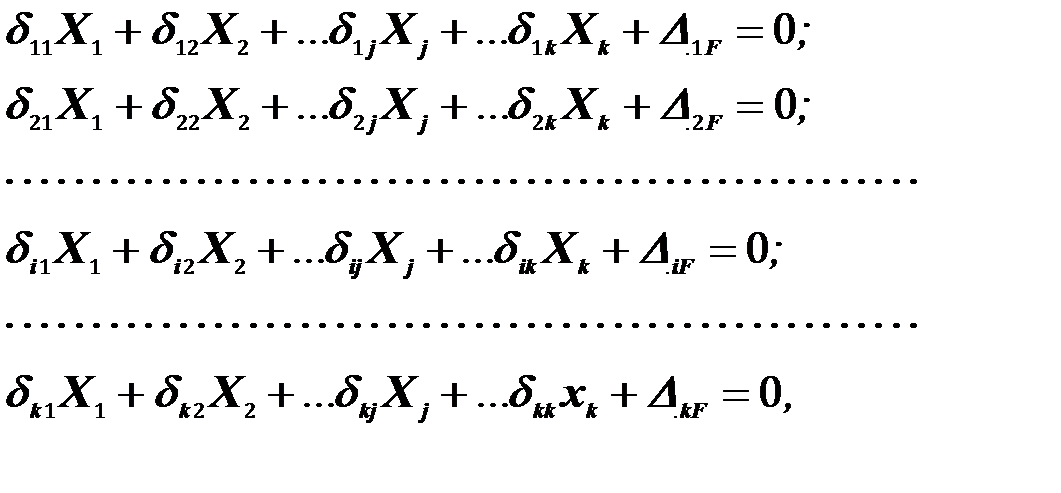 (21)
(21)
где 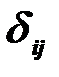 - перемещение точки приложения силы Х i в направлении этой силы от силы Х j=1;
- перемещение точки приложения силы Х i в направлении этой силы от силы Х j=1;
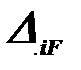 - перемещение точки приложения силы Х i в направлении этой силы от известной внешней нагрузки.
- перемещение точки приложения силы Х i в направлении этой силы от известной внешней нагрузки.
Приведенные уравнения (20) называются каноническими уравнениями метода сил. Количество их всегда равно степени статической неопределимости заданной системы. Для раскрытия статической неопределимости необходимо решить систему канонических уравнений, т.е. найти величины Х1, Х2 … Х k . Для этого, очевидно, надо знать величину коэффициентов 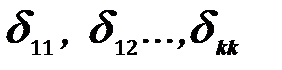 и свободных членов
и свободных членов 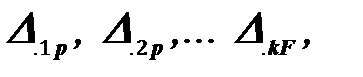 входящих в канонические уравнения. Эти коэффициенты по физическому смыслу представляют собой перемещения, поэтому определить их можно в общем случае с помощью интегралов Максвелла-Мора.
входящих в канонические уравнения. Эти коэффициенты по физическому смыслу представляют собой перемещения, поэтому определить их можно в общем случае с помощью интегралов Максвелла-Мора.
Для плоской рамы, состоящей из прямолинейных стержней или балки, коэффициенты канонических уравнений можно вычислить по способу Верещагина.
Пример расчета статически неопределимой балки
Пример 1. Раскрыть статическую неопределимость, построить эпюры изгибающих моментов и поперечных сил для балки, изображенной на рис. 16. Составить условие прочности, если
а=1м, d=0,02 м, М=25 кНм, q=20 кН/м, [σ]=160 МПа.
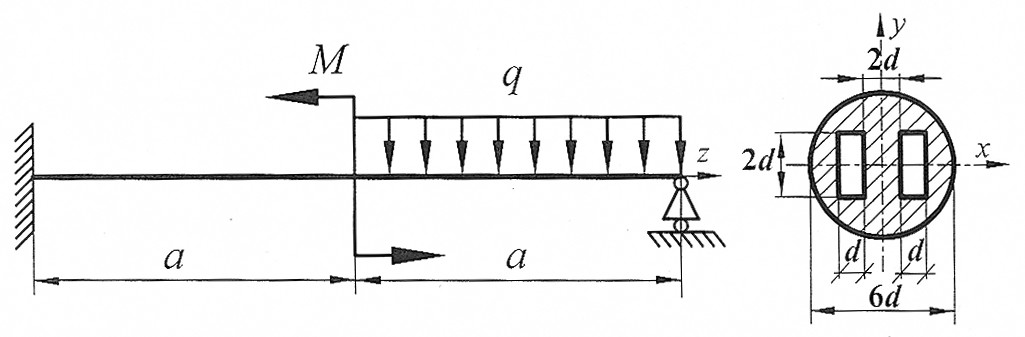
Рис. 16
Решение.
Определяем степень статической неопределимости.
Для этого обозначим реакции опор (рис. 17, а) и составим уравнения статики:
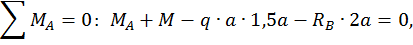
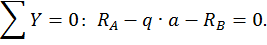
Данная балка 1 раз статически неопределимая, так как имеем 3 неизвестных и только 2 независимых уравнений статики:
k = 3– 2 = 1.
Выбираем основную систему, удаляя «лишнюю» связь.
За лишнее закрепление примем шарнирно-подвижную опору В. Основная система балки показана на рис. 17, б. «Лишнюю» связь заменяем силой Х1 (рис. 17, в).
Записываем каноническое уравнение метода сил:
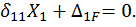
Отброшенная связь не допускают перемещений, поэтому в правой части уравнения стоит ноль.
Вычисляем коэффициенты канонических уравнений по способу Верещагина. Рассматриваемая балка работает главным образом на изгиб, поэтому сдвигом балки будем пренебрегать. Коэффициенты канонического уравнения вычисляем по формуле
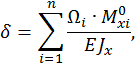
где 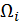 – площадь эпюры изгибающего момента от заданной нагрузки
– площадь эпюры изгибающего момента от заданной нагрузки
на i-м участке (её часто называют грузовой площадью);
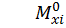 – ордината эпюры изгибающих моментов от единичной
– ордината эпюры изгибающих моментов от единичной
нагрузки, взятая под центром тяжести первой эпюры;
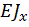 – жесткость балки.
– жесткость балки.
Предварительно строим эпюры изгибающих моментов от заданной внешней нагрузки и единичной нагрузок (Х1=1) (рис. 17, д, ж).
Построим эпюры изгибающего момента  от внешней нагрузки (грузовую эпюру, рис. 17, д):
от внешней нагрузки (грузовую эпюру, рис. 17, д):
Первый участок: 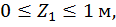
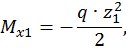
при  :
:
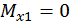 ,
,
при 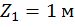 :
:
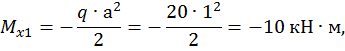
Второй участок: 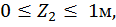
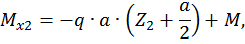
при 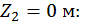
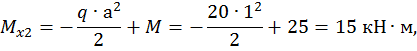
при 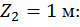
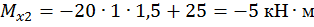 .
.
Построим эпюры изгибающего момента  от единичной нагрузки (единичную эпюру, рис. 17, г):
от единичной нагрузки (единичную эпюру, рис. 17, г):
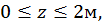
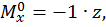
при 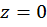 :
:
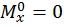 ,
,
при 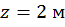 :
:
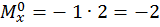 .
.
Коэффициент 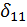 определяем “перемножением” эпюры
определяем “перемножением” эпюры 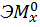 самой на себя.
самой на себя.
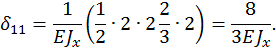
Грузовой коэффициент 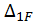 находим “перемножением” грузовой эпюры
находим “перемножением” грузовой эпюры 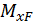 на эпюру от единичной нагрузки. Для этого грузовую эпюру разбиваем на два обычных треугольника, один сверху от оси z, другой снизу от оси z, и на «параболический» треугольник.
на эпюру от единичной нагрузки. Для этого грузовую эпюру разбиваем на два обычных треугольника, один сверху от оси z, другой снизу от оси z, и на «параболический» треугольник.
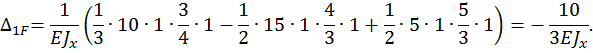
Определяем неизвестную 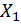 , решая каноническое уравнение
, решая каноническое уравнение
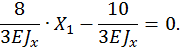
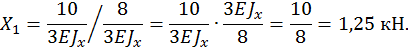
Таким образом, статическая неопределимость раскрыта.
Построим эпюру поперечных сил 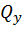 (рис. 18, б).
(рис. 18, б).
Первый участок: 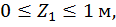
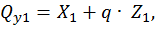
при  :
:
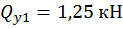 ,
,
при 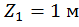 :
:
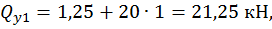
Второй участок: 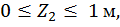
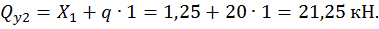
Построим эпюру изгибающих моментов  (рис. 18, в).
(рис. 18, в).
Первый участок: 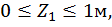
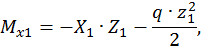
при  :
:
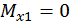 ,
,
при 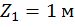 :
:
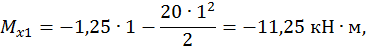
Второй участок: 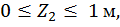
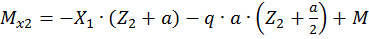 ,
,
при 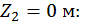
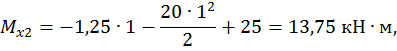
при 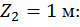
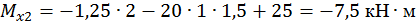 .
.
Проверка расчета. Обычно проводится деформационная проверка. При деформационной проверке производится перемножение по способу Верещагина эпюры изгибающих моментов, построенной для заданной балки, на эпюру изгибающих моментов от единичной нагрузки (рис. 18, в, д). Для этого грузовую эпюру разбиваем на три треугольника, один сверху от оси z, два снизу от оси z, и фигуру, очерченную квадратичной параболой.
В результате перемножения вертикальное перемещение должно быть равно нулю.
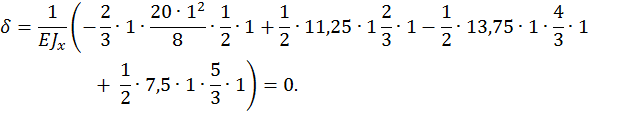
Деформационная проверка подтвердила правильность расчета.
Составим условие прочности по формуле
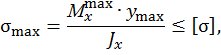
где
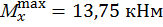 ,
,
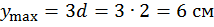 .
.
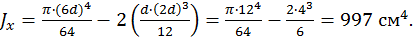
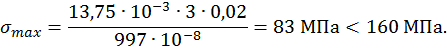
Таким образом, условие прочности выполняется.
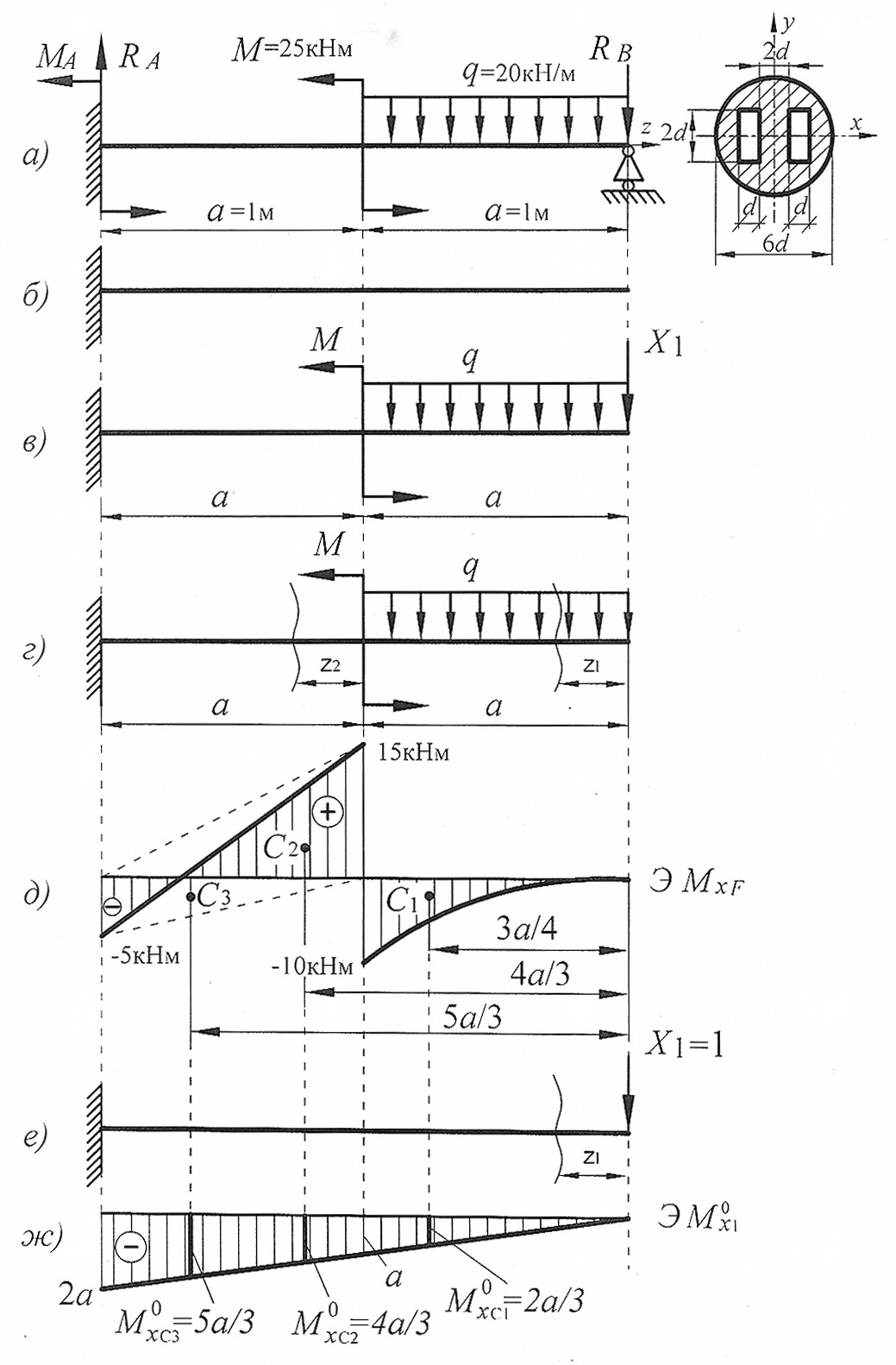 Рис. 17
Рис. 17
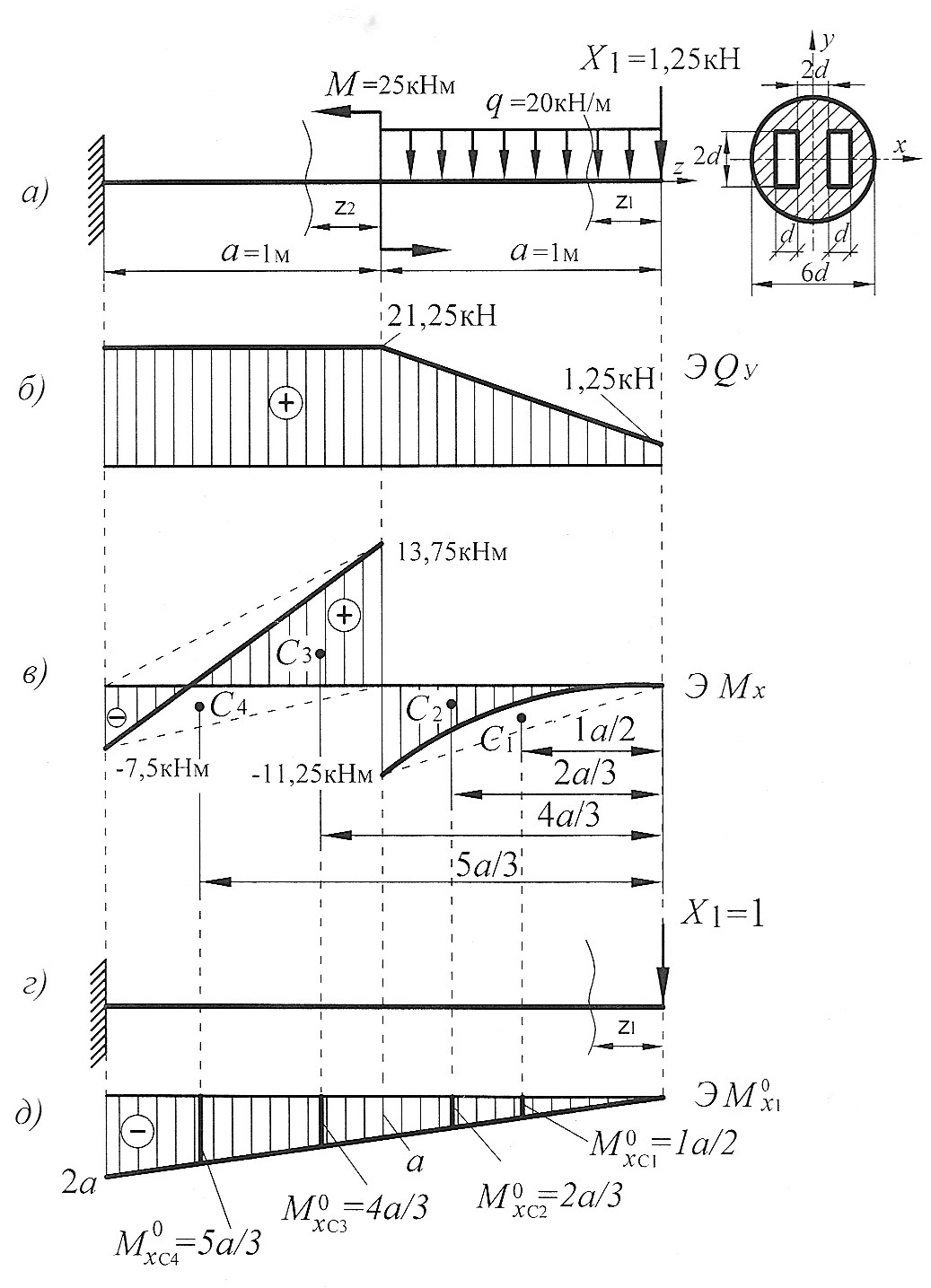
Рис. 18
Пример расчета статически неопределимой рамы
Пример 1. Раскрыть статическую неопределимость рамы (рис. 19). Построить эпюры продольных, поперечных сил и изгибающих моментов. Составить условие прочности, из условия прочности подобрать размеры поперечного сечения. Найти горизонтальное перемещения сечения С и угол поворота сечения D. Дано: F =20 кН, а=2 м, М= F 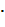 a,
a, 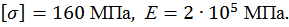
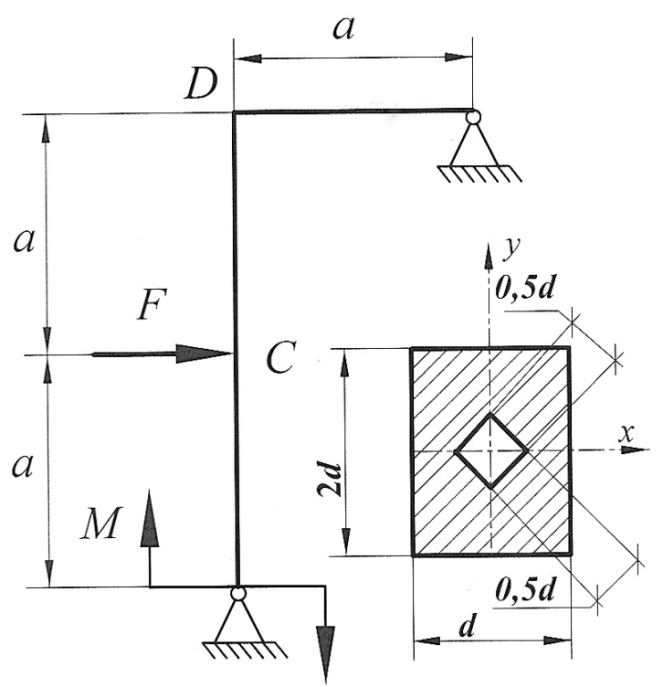
Рис. 19
Решение.
Определяем степень статической неопределимости.
Для этого обозначим реакции опор (рис. 20, а) и составим уравнения статики:
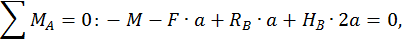
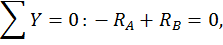
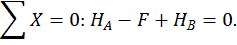
Данная рама 1 раз статически неопределимая, так как имеем 4 неизвестных и только 3 независимых уравнений статики:
k = 4– 3 = 1.
Выбираем основную систему, удаляя «лишнюю» связь.
За «лишнее» закрепление примем горизонтальное закрепление в шарнирно-неподвижной опоре В. Заменим шарнирно-неподвижную опору шарнирно-подвижной. Основная система балки показана на рис. 20, б. «Лишнюю» связь заменяем силой Х1 (рис. 20, в).
Записываем каноническое уравнение метода сил:
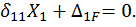
Отброшенная связь не допускает горизонтального перемещения, поэтому в правой части уравнения стоит ноль.
Вычисляем коэффициенты канонических уравнений по способу Верещагина. Рассматриваемая рама работает главным образом на изгиб, поэтому сдвигом и растяжением (сжатием) рамы будем пренебрегать. Коэффициенты канонического уравнения вычисляем по формуле
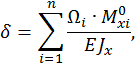
где 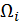 – площадь эпюры изгибающего момента от заданной нагрузки
– площадь эпюры изгибающего момента от заданной нагрузки
на i -м участке (её часто называют грузовой площадью);
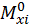 – ордината эпюры изгибающих моментов от единичной
– ордината эпюры изгибающих моментов от единичной
нагрузки, взятая под центром тяжести первой эпюры;
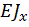 – жесткость балки.
– жесткость балки.
Предварительно строим эпюры изгибающих моментов от заданной внешней нагрузки (рис. 20, г) и единичной нагрузки Х1=1 (рис. 20, д).
Построим эпюры изгибающего момента  от внешней нагрузки (грузовую эпюру, рис. 21, а). Для этого определим опорные реакции из уравнений статики:
от внешней нагрузки (грузовую эпюру, рис. 21, а). Для этого определим опорные реакции из уравнений статики:
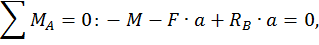
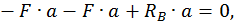
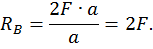
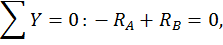
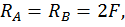
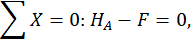
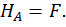
Составим выражения для изгибающих моментов на каждом участке.
Первый участок: 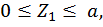
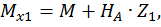
при  :
:
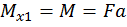 ,
,
при 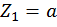 :
:
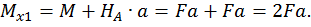
Второй участок: 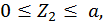
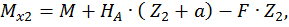
при 
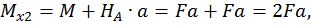
при 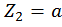 :
:
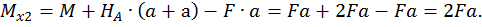
Третий участок: 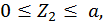
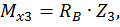
при 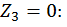
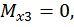
при 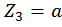 :
:
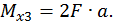
Построим эпюры изгибающего момента  от единичной нагрузки Х1 =1 (единичную эпюру, рис. 21, б). Для этого определим опорные реакции:
от единичной нагрузки Х1 =1 (единичную эпюру, рис. 21, б). Для этого определим опорные реакции:
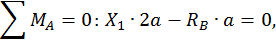
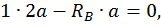
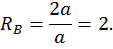
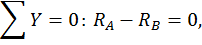
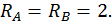
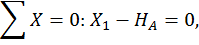
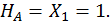
Составим выражения для изгибающих моментов на каждом участке.
Первый участок: 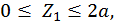
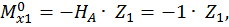
при  :
:
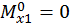 ,
,
при 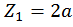 :
:
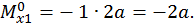
Второй участок: 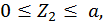
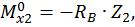
при 
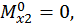
при 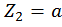 :
:
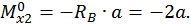
Коэффициент 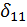 определяем «перемножением» эпюры
определяем «перемножением» эпюры 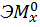 самой на себя.
самой на себя.
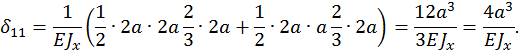
Грузовой коэффициент 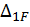 находим «перемножением» грузовой эпюры
находим «перемножением» грузовой эпюры 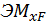 (см. рис. 21, а) на эпюру от единичной нагрузки
(см. рис. 21, а) на эпюру от единичной нагрузки 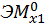 (рис. 21б). Для этого грузовую эпюру разбиваем на три треугольника и на прямоугольник (см. рис. 21, а).
(рис. 21б). Для этого грузовую эпюру разбиваем на три треугольника и на прямоугольник (см. рис. 21, а).
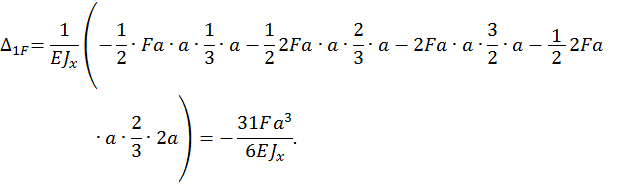
Определяем неизвестную 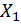 , решая каноническое уравнение
, решая каноническое уравнение
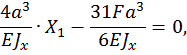
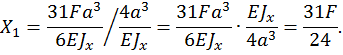
Таким образом, статическая неопределимость раскрыта.
Строим эпюры продольных, поперечных сил и изгибающих моментов. Для этого определим опорные реакции из уравнений статики:
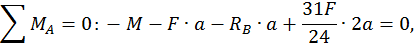
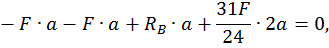
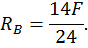
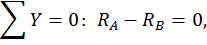
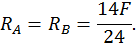
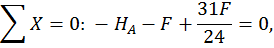
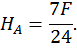
Построим эпюру продольных сил 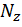 (рис. 22, а).
(рис. 22, а).
Первый участок: 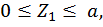
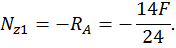
Второй участок: 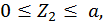
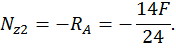
Третий участок: 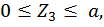
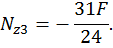
Построим эпюру поперечных сил 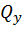 (рис. 22, б).
(рис. 22, б).
Первый участок: 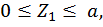
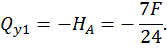
Второй участок: 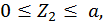
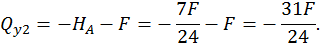
Третий участок: 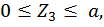
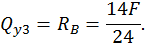
Построим эпюру изгибающих моментов  (рис. 22, в).
(рис. 22, в).
Первый участок: 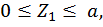
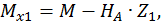
при  :
:
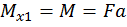 ,
,
при 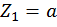 :
:
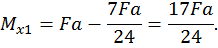
Второй участок: 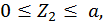
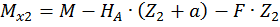 ,
,
при 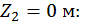
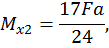
при 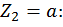
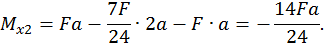
Третий участок: 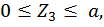
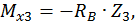
при 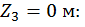
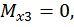
при 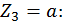
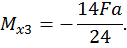
Проверка расчета. Обычно проводится деформационная проверка. При деформационной проверке производится перемножение по способу Верещагина эпюры изгибающих моментов, построенной для заданной рамы (рис 22в), на эпюру изгибающих моментов от единичной нагрузки (рис. 22, г). Для этого грузовую эпюру разбиваем на пять треугольников (см. рис. 22, в).
В результате перемножения горизонтальное перемещение должно быть равно нулю.
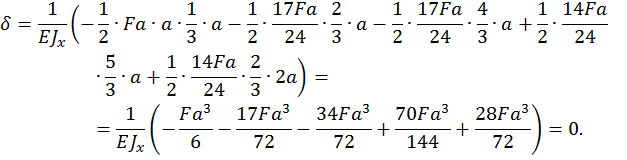
Деформационная проверка подтвердила правильность расчета.
Составим условие прочности по формуле
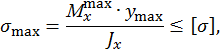
где  ,
,
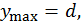
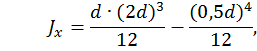
тогда
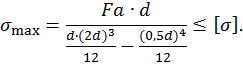
Подставив значения F =20 кН, а=2 м, 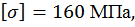 из условия прочности определим размеры поперечного сечения:
из условия прочности определим размеры поперечного сечения:
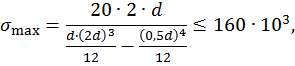
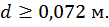
Принимаем 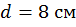 ,
, 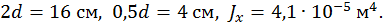
Определим горизонтальное перемещение сечения С. Для этого строим эпюру изгибающих моментов (единичную эпюру рис. 23, б) от горизонтальной единичной силы 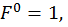 приложенной в точке С (рис. 23, а). Для этого определим опорные реакции из уравнений статики:
приложенной в точке С (рис. 23, а). Для этого определим опорные реакции из уравнений статики:
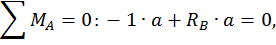
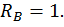
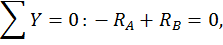
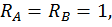
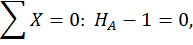
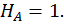
Составим выражения для изгибающих моментов на каждом участке.
Первый участок: 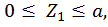
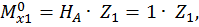
при  :
:
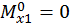 ,
,
при 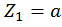 :
:
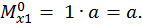
Второй участок: 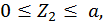
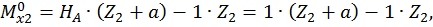
при 
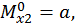
при 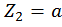 :
:
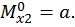
Третий участок: 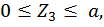
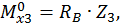
при 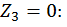
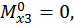
при 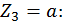
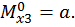
Для определения горизонтального перемещения сечения С перемножаем данную единичную эпюру (см. рис. 23, б) и эпюру изгибающих моментов для заданной рамы (рис. 22, в):
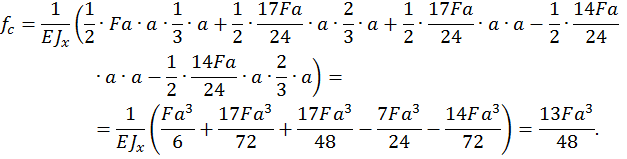
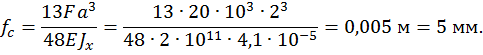
Определим угол поворота сечения D. Для этого строим эпюру изгибающих моментов, единичную эпюру (рис. 23, г) от единичного момента 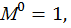 приложенного в сечении D (см. рис. 23, в). Для этого определим опорные реакции из уравнений статики:
приложенного в сечении D (см. рис. 23, в). Для этого определим опорные реакции из уравнений статики:
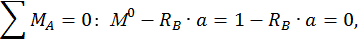
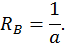
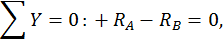
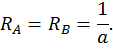
Составим выражения для изгибающих моментов на каждом участке.
Первый участок: 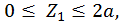
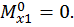
Второй участок: 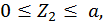
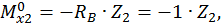
при 
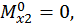
при 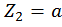 :
:
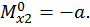
Для определения угла поворота сечения D перемножаем данную единичную эпюру (см. рис. 23, г) и эпюру изгибающих моментов для заданной рамы (см. рис. 22, в):
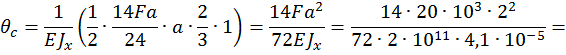
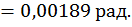
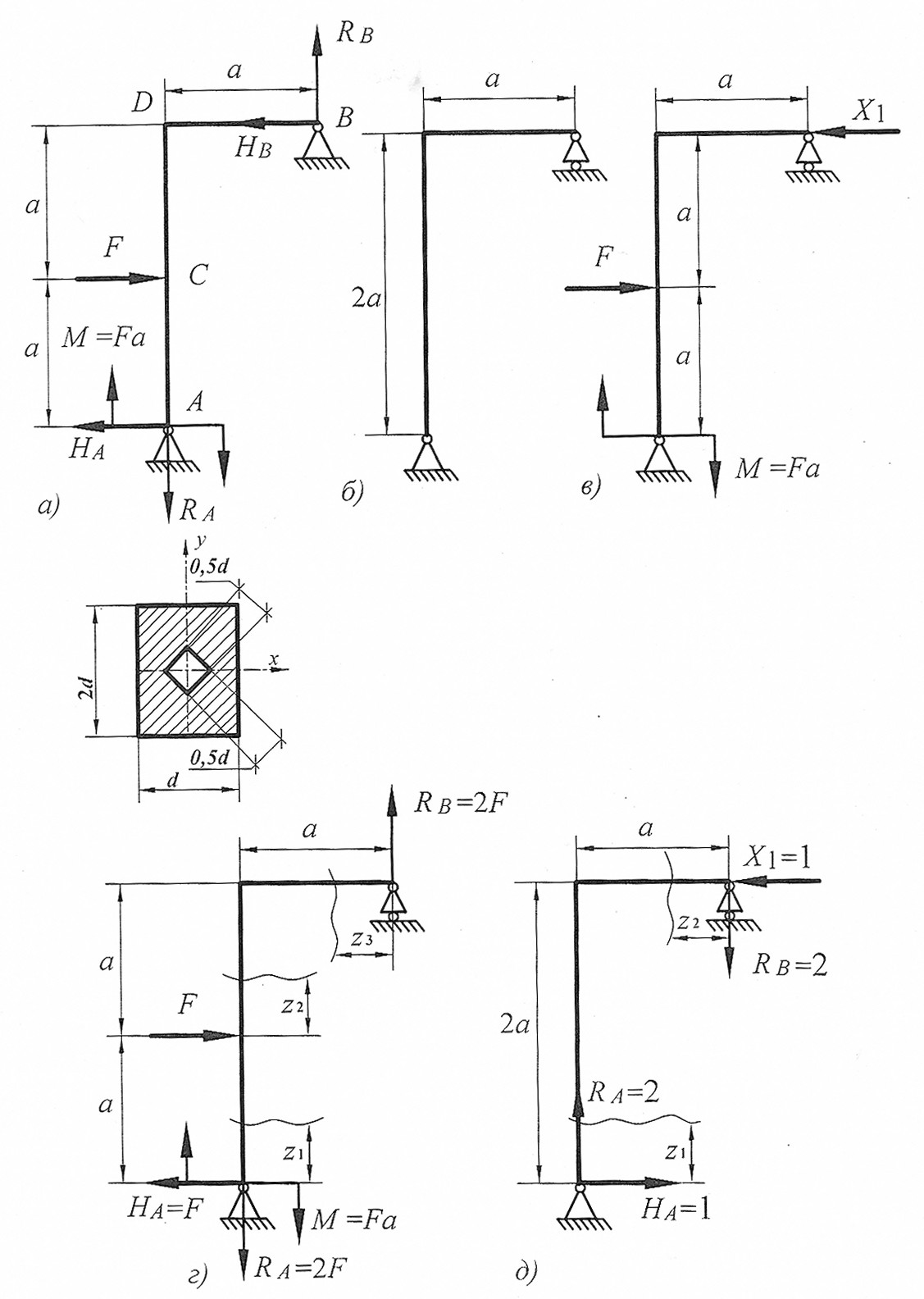
Рис. 20
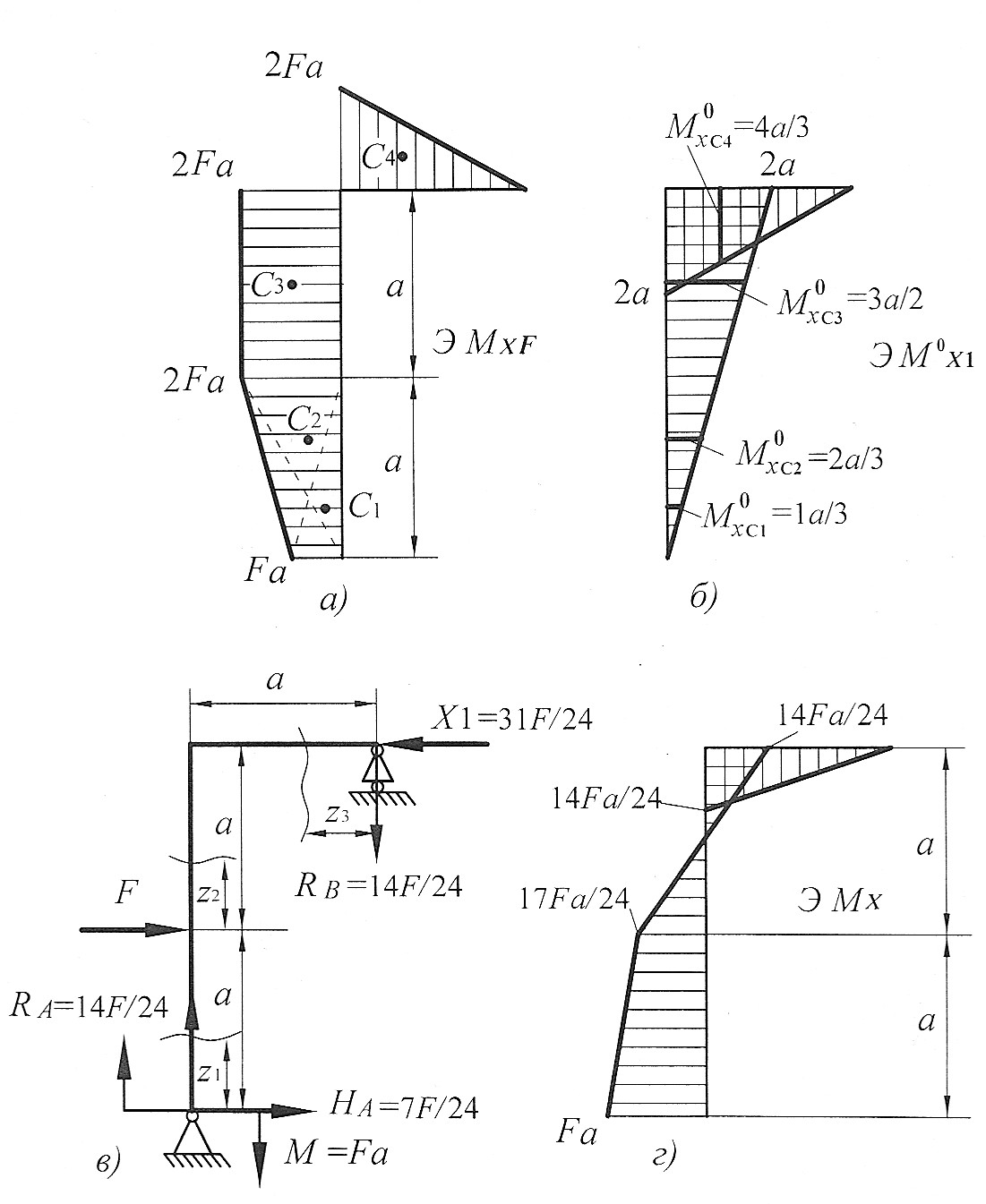
Рис. 21
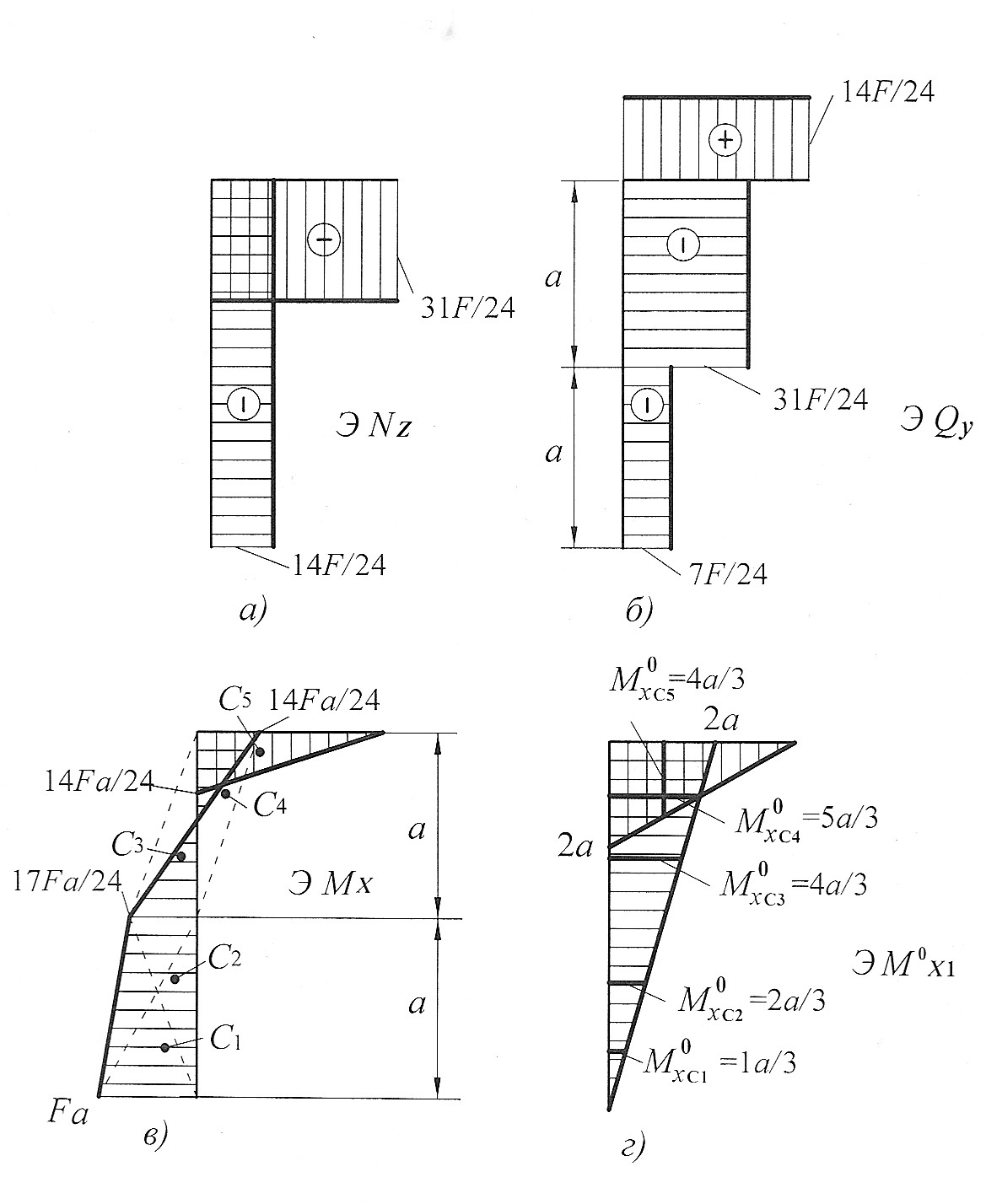
Рис. 22
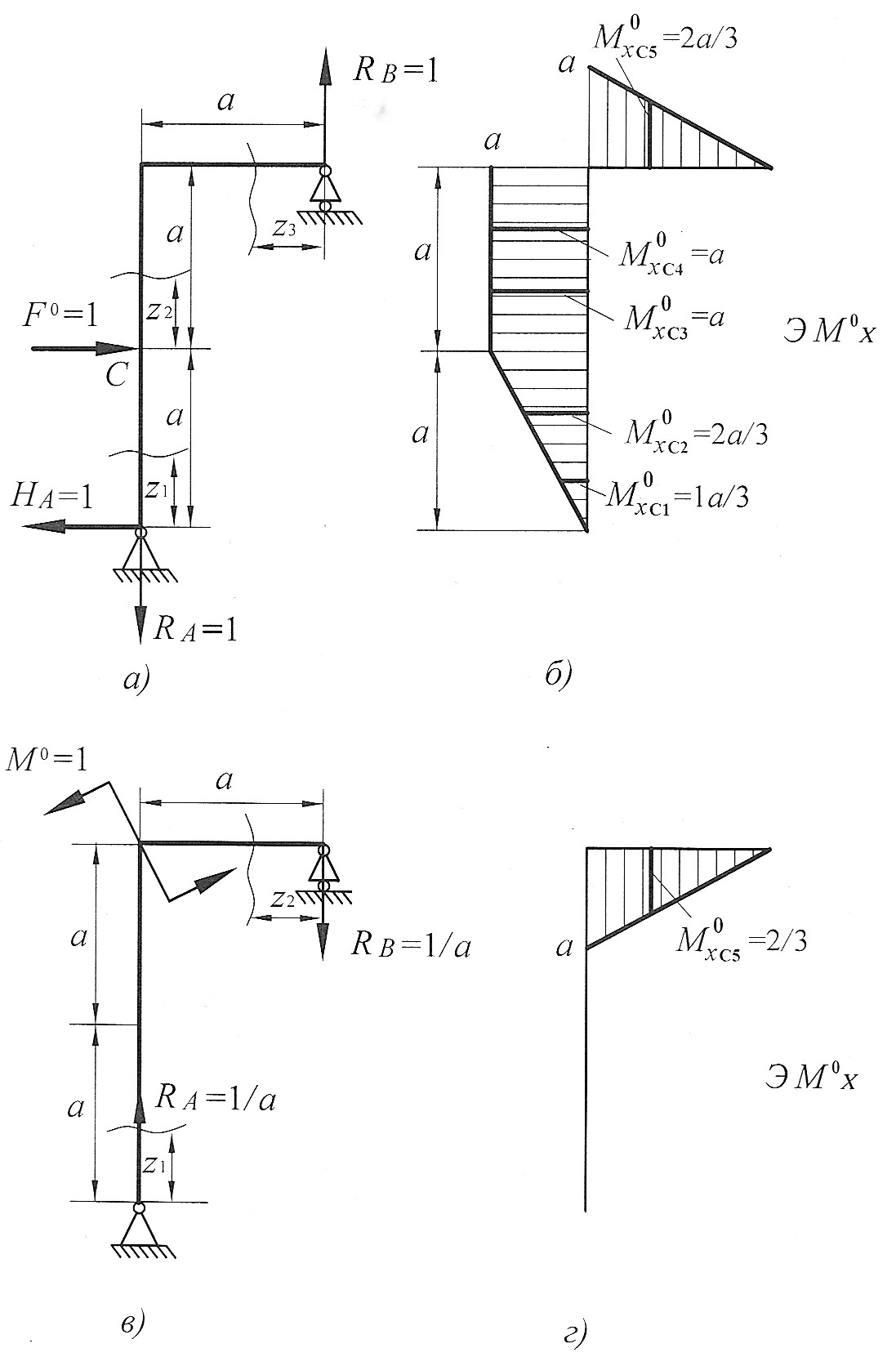
Рис. 23
Статической неопределимости
Положим, имеется некоторая симметричная, в геометрическом смысле, рама (рис. 24, а). Ее правую часть можно рассматривать как зеркальное отображение левой части относительно плоскости симметрии. При расчете таких рам оказывается возможным упростить решение задачи и уменьшить число искомых силовых факторов.
Рассмотрим случаи нагружения рамы симметричной (рис. 24, б) и кососимметричной (рис. 24, в) нагрузками. Под симметричной нагрузкой будем понимать такую нагрузку, при которой все внешние силы, приложенные к правой части рамы, являются зеркальным отображением сил, приложенных к ее левой части (см. рис. 24, б). Под кососимметричной, или антисимметричной, нагрузкой будем понимать такую нагрузку, при которой силы, приложенные к правой половине рамы, также являются зеркальным отображением сил, приложенных к ее левой половине, но противоположны им по знаку (см. рис. 24, в).

Рис. 24
Аналогично классифицируем и внутренние силовые факторы. Рассмотрим для этого некоторое произвольное сечение рамы, в котором возникает шесть силовых факторов. В правой и левой частях бруса (рис. 25) внутренние силы и моменты равны. Посмотрим, какие из шести силовых факторов образуют зеркальное отображение относительно плоскости сечения. Такими оказываются три фактора: два изгибающих момента и нормальная сила. Будем их называть симметричными внутренними факторами. Крутящий момент и обе поперечные силы в принятой терминологии должны быть названы кососимметричными факторами. Каждый из них противоположен по знаку зеркальному отображению взаимного фактора.
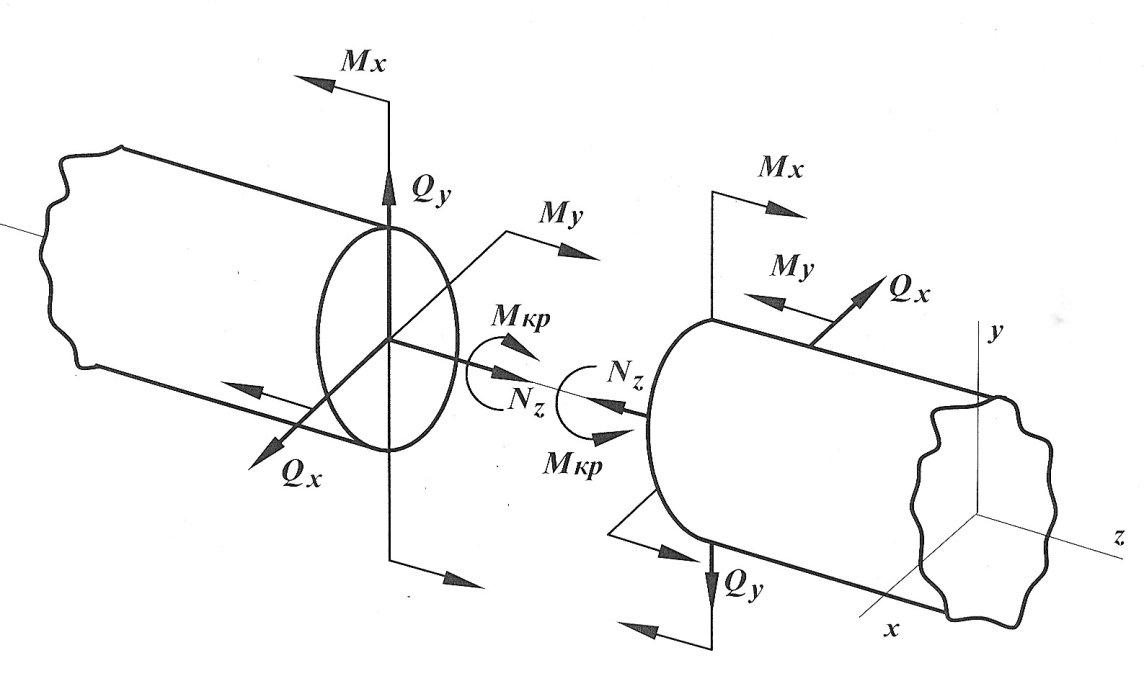
Рис. 25
Обратимся к симметричной раме, например, показанной на рис. 24, б, и выберем основную систему, разрезая раму по плоскости симметрии (рис. 26).
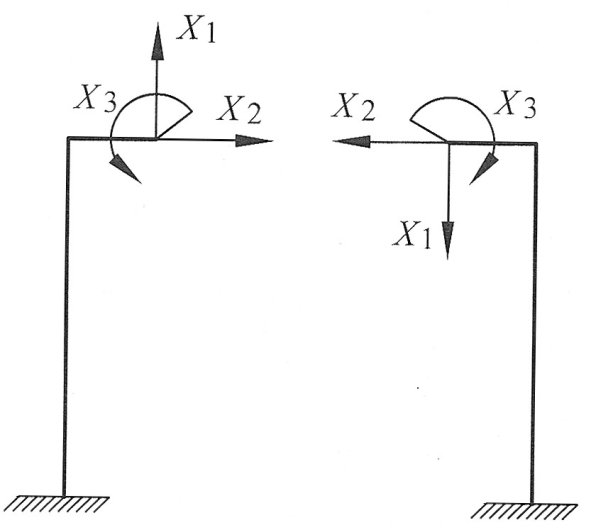
Рис. 26
Обозначим через 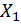 кососимметричный, а через
кососимметричный, а через 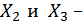 симметричные силовые факторы и выпишем систему канонических уравнений. В данном случае их будет три:
симметричные силовые факторы и выпишем систему канонических уравнений. В данном случае их будет три:
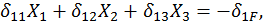
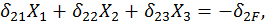 (23)
(23)
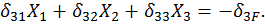
Прежде всего необходимо отметить, что независимо от характера внешней нагрузки все коэффициенты 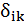 , у которых один индекс принадлежит симметричному, а второй кососимметричному силовому фактору, равны нулю, то есть
, у которых один индекс принадлежит симметричному, а второй кососимметричному силовому фактору, равны нулю, то есть 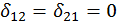 ,
, 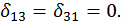 Кроме того, если предположить, что внешняя нагрузка F симметричная, то дополнительно
Кроме того, если предположить, что внешняя нагрузка F симметричная, то дополнительно 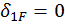 и
и 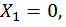 тогда система уравнений (23) примет вид
тогда система уравнений (23) примет вид
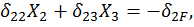
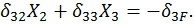 (24)
(24)
Если же внешняя нагрузка кососимметричная, то коэффициенты 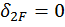 и
и 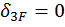 , а также
, а также 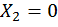 и
и 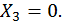 В этом случае система уравнений примет вид:
В этом случае система уравнений примет вид:
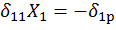 . (25)
. (25)
Происходит это потому, что в симметричной раме не возникает взаимных кососимметричных перемещений под действием симметрич-ных нагрузок. Точно так же не возникает симметричных перемещений под действием кососимметричных факторов. Сказанное становится еще более очевидным, если учесть, что в рассматриваемой системе эпюра изгибающих моментов от кососимметричных факторов будет кососим-метричной, а от симметричных факторов - симметричной. При перемно-жении таких эпюр, естественно, получим нуль, в то время как перемно-жение кососимметричной эпюры на кососимметричную и симметричной на симметричную эпюру, дает результат, отличный от нуля.
Пример расчета симметричной статически
Нагрузкой
Пример 1. Раскрыть статическую неопределимость и построить эпюру изгибающих моментов для рамы, показанной на рис. 27.
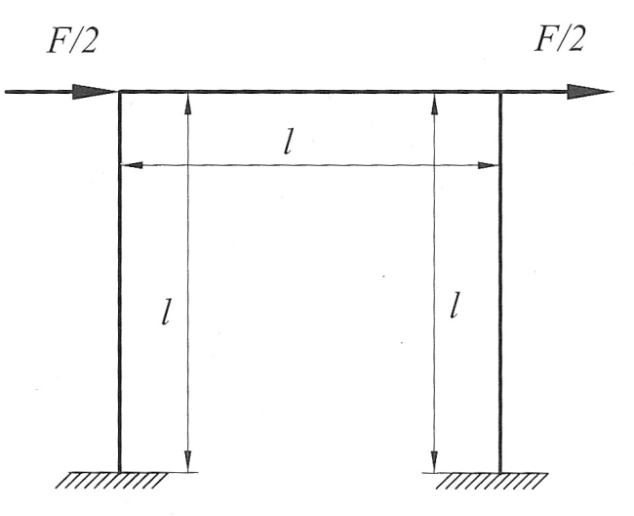
Рис. 27
Решение.
Определяем степень статической неопределимости.
Разрезаем раму по оси симметрии, получаем две половины рамы. Прикладываем внутренние силовые факторы к обеим половинам рамы. Их шесть: две продольные силы, две поперечные силы и два изгибающих момента (рис. 28, а, б). Данная рама три раза статически неопределимая, так как имеем 6 неизвестных и только три независимых уравнения статики:
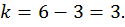
Рама симметричная и нагружена кососимметрично расположенными силами. При кососимметричной внешней нагрузке обращаются в нуль симметричные силовые факторы (рис. 28, в), т.е. продольные силы (  и изгибающие моменты
и изгибающие моменты 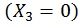 , а также коэффициенты
, а также коэффициенты 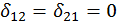 ,
, 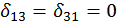 ,
, 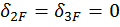 . Взамен трех уравнений получаем одно:
. Взамен трех уравнений получаем одно:
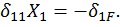
Вычисляем коэффициенты канонических уравнений по способу Верещагина.
Построим эпюры изгибающего момента  от внешней нагрузки для первой половины рамы (рис. 29, а).
от внешней нагрузки для первой половины рамы (рис. 29, а).
Составим выражения для изгибающих моментов на каждом участке.
Первый участок: 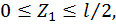
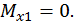
Второй участок: 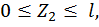
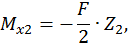
при 
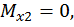
при 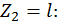
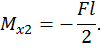
Построим эпюры изгибающего момента  от внешней нагрузки для второй половины рамы (рис. 29, б).
от внешней нагрузки для второй половины рамы (рис. 29, б).
Составим выражение для изгибающих моментов на каждом участке.
Первый участок: 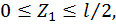
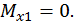
Второй участок: 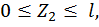
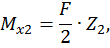
при 
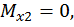
при 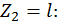
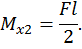
Построим эпюры изгибающего момента  от единичной нагрузки
от единичной нагрузки 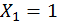 (единичную эпюру, рис. 29, в) для первой половины рамы.
(единичную эпюру, рис. 29, в) для первой половины рамы.
Составим выражения для изгибающих моментов на каждом участке.
Первый участок: 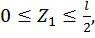
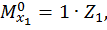
при 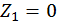 :
:
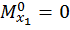 ,
,
при 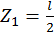 :
:
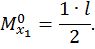
Второй участок: 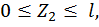
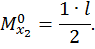
Построим эпюры изгибающего момента  от единичной нагрузки
от единичной нагрузки 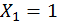 (единичную эпюру, рис. 29, г) для второй половины рамы.
(единичную эпюру, рис. 29, г) для второй половины рамы.
Составим выражение для изгибающих моментов на каждом участке.
Первый участок: 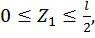
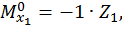
при 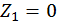 :
:
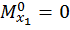 ,
,
при 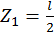 :
:
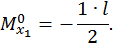
Второй участок: 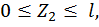
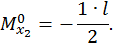
Коэффициент 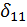 определяем «перемножением» эпюры
определяем «перемножением» эпюры 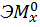 самой на себя (см. рис. 29 в, г).
самой на себя (см. рис. 29 в, г).
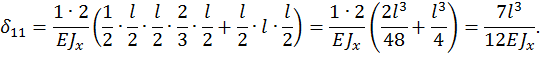
Грузовой коэффициент 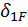 находим «перемножением» грузовой эпюры
находим «перемножением» грузовой эпюры 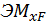 (рис. 29, а, б) на эпюру от единичной нагрузки
(рис. 29, а, б) на эпюру от единичной нагрузки 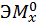 (рис. 29, в, г).
(рис. 29, в, г).
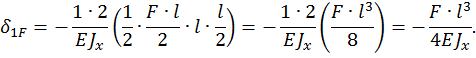
Определяем неизвестную 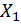 , решая каноническое уравнение
, решая каноническое уравнение
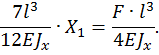
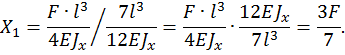
Таким образом, статическая неопределимость раскрыта.
Построим эпюры изгибающего момента для первой половины заданной рамы (рис. 30, а).
Составим выражение для изгибающих моментов на каждом участке:
Первый участок: 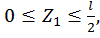
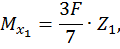
при 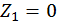 :
:
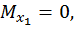
при 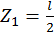 :
:
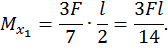
Второй участок: 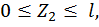
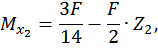
при 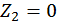 :
:
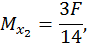
при 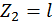 :
:
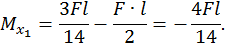
Построим эпюры изгибающего момента для второй половины заданной рамы (рис. 30, б).
Составим выражение для изгибающих моментов на каждом участке.
Первый участок: 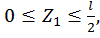
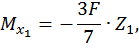
при 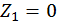 :
:
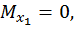
при 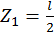 :
:
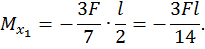
Второй участок: 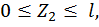
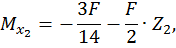
при 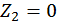 :
:
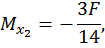
при 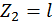 :
:
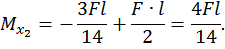
Объединяем обе эпюры, получившаяся эпюра является эпюрой изгибающих моментов для заданной рамы (рис. 30, в).
Максимальный изгибающий момент возникает в левой и правой опорах:
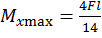 .
.
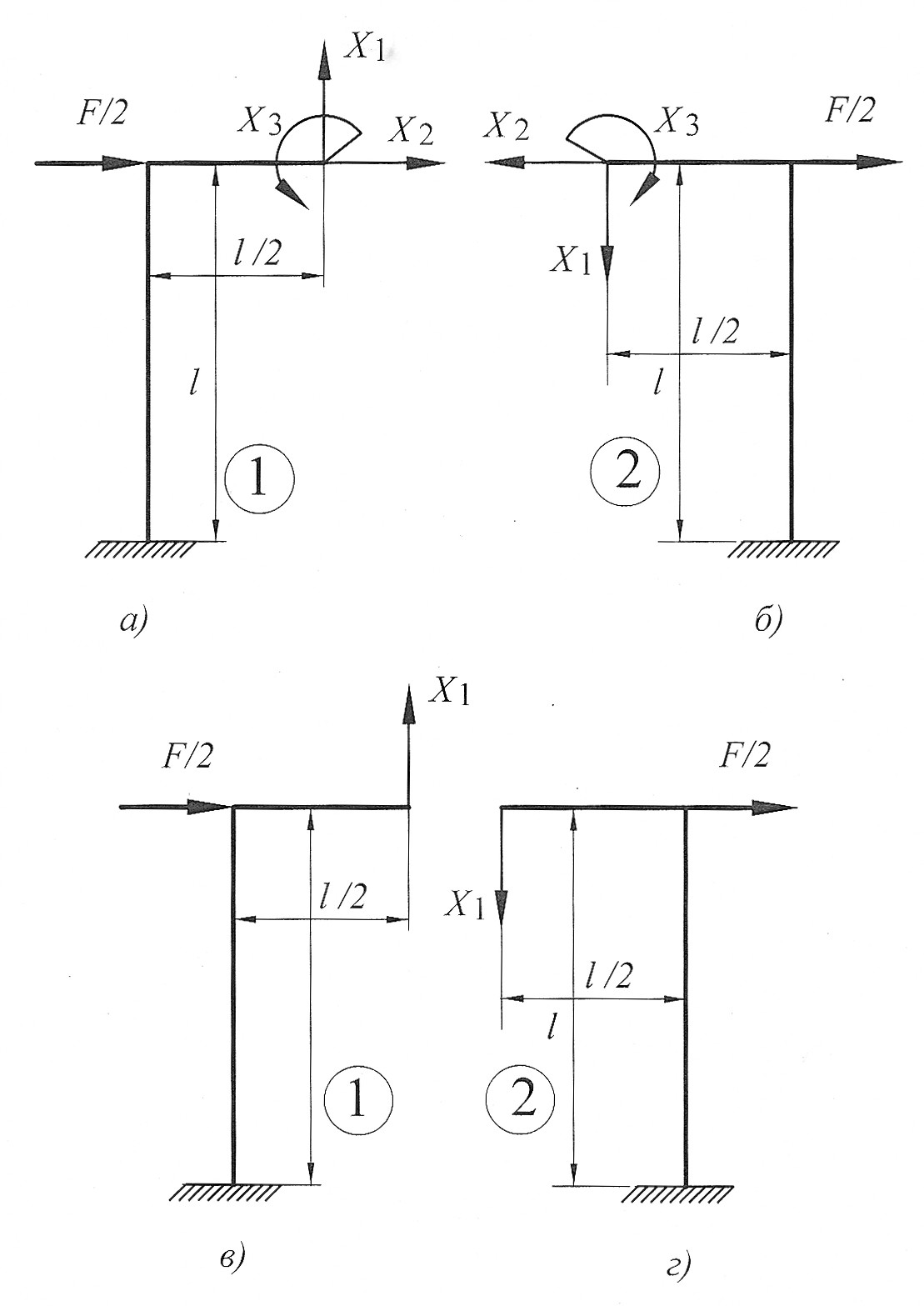 Рис. 28
Рис. 28
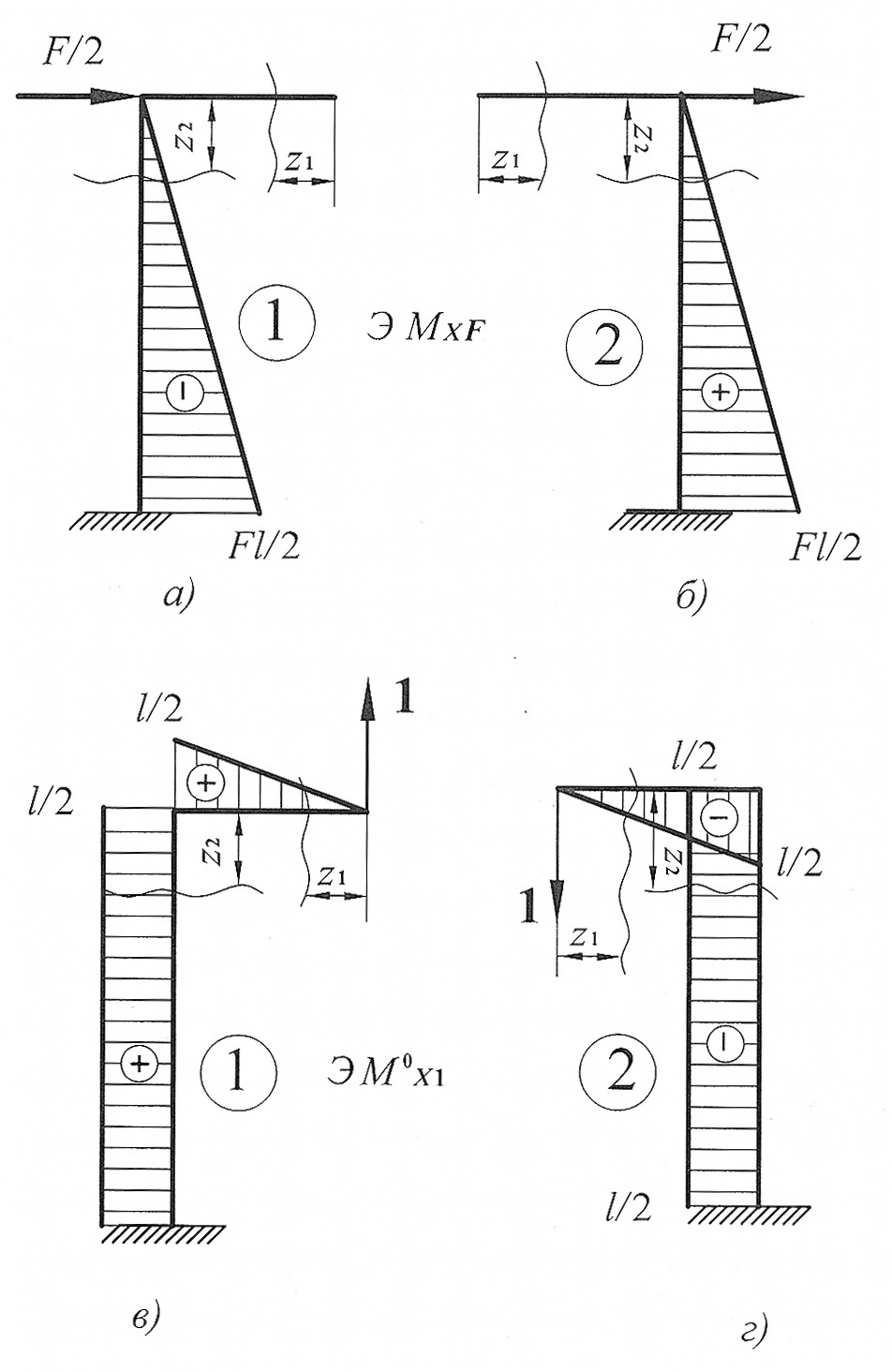
Рис. 29
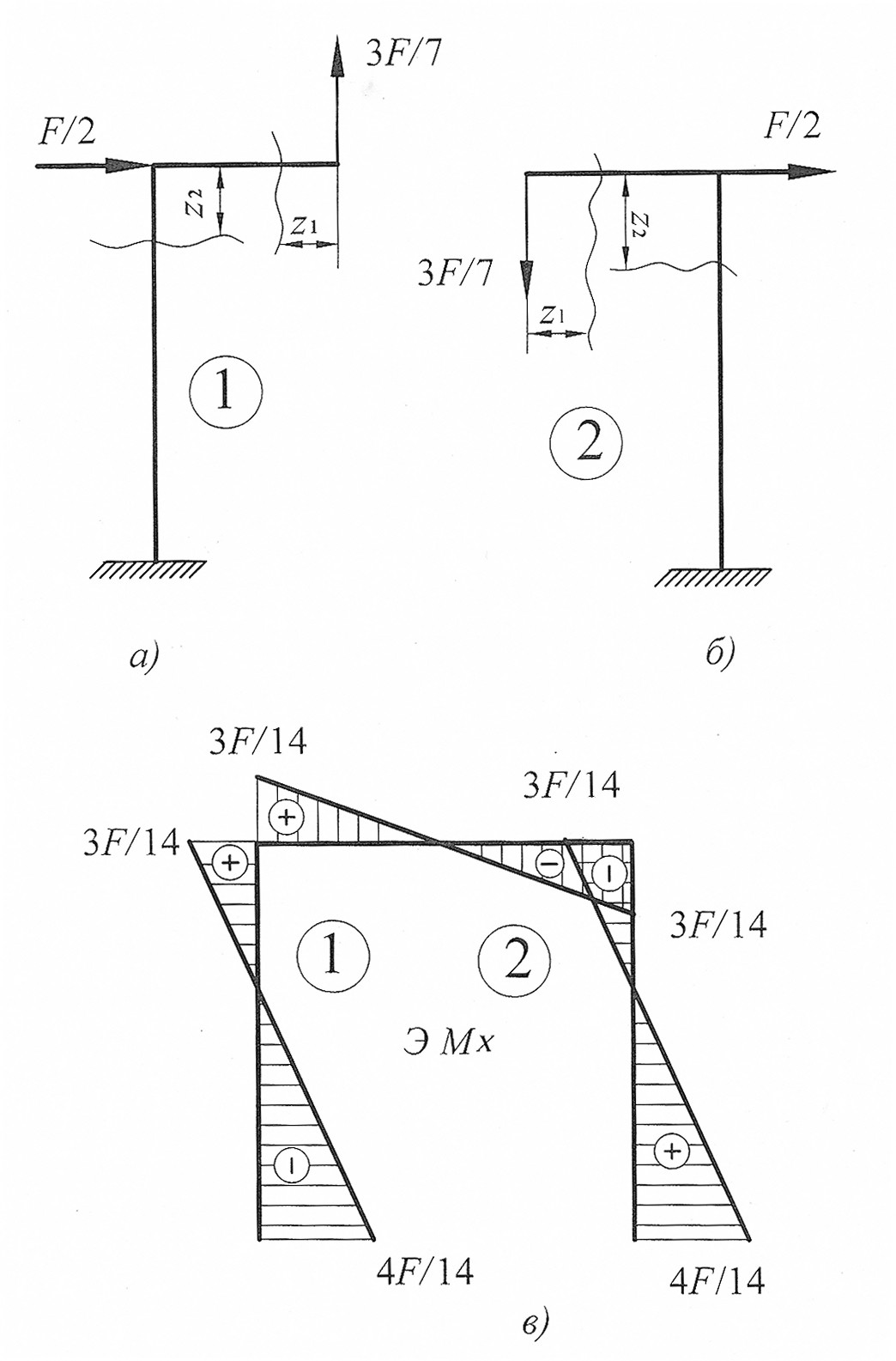 Рис. 30
Рис. 30
ЗАДАЧИ ДЛЯ ПРОВЕРКИ СТУДЕНТАМИ СТЕПЕНИ УСВОЕНИЯ МАТЕРИАЛА РАЗДЕЛА «СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ»
Задача 1
Раскрыть статическую неопределимость, построить эпюры 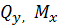 изображенной на рисунке балки. изображенной на рисунке балки.
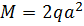 , ,

|
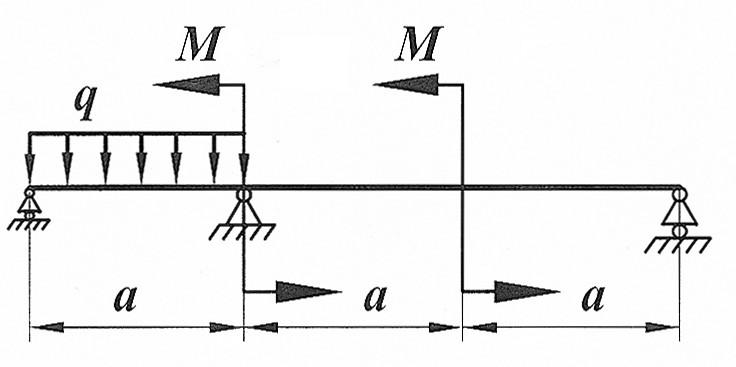
|
Задача 2
Раскрыть статическую неопределимость, построить эпюры 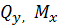 изображенной на рисунке балки. изображенной на рисунке балки.
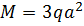 , ,

|
|
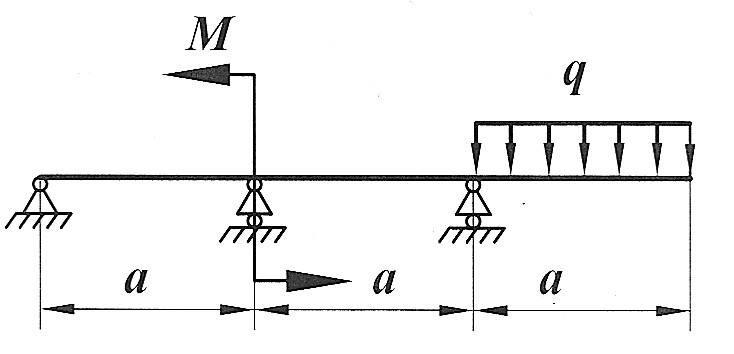
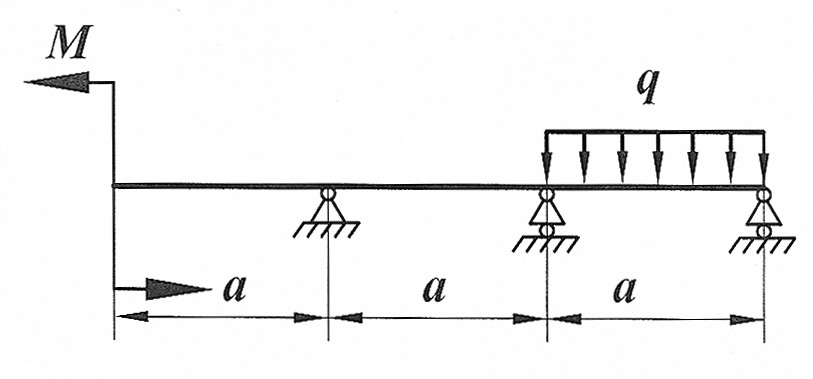
Задача 3
Раскрыть статическую неопределимость, построить эпюры 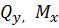 изображенной на рисунке балки. изображенной на рисунке балки.
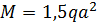 , ,

|
|
Задача 4
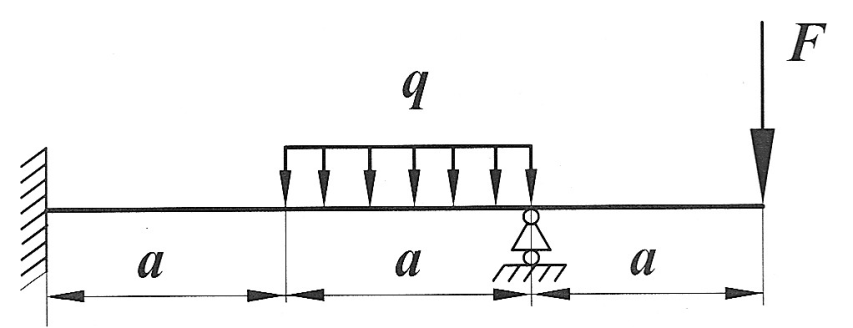
|
Раскрыть статическую неопределимость, построить эпюры 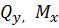 изображенной на рисунке балки. изображенной на рисунке балки.
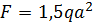 , ,

|
Задача 5
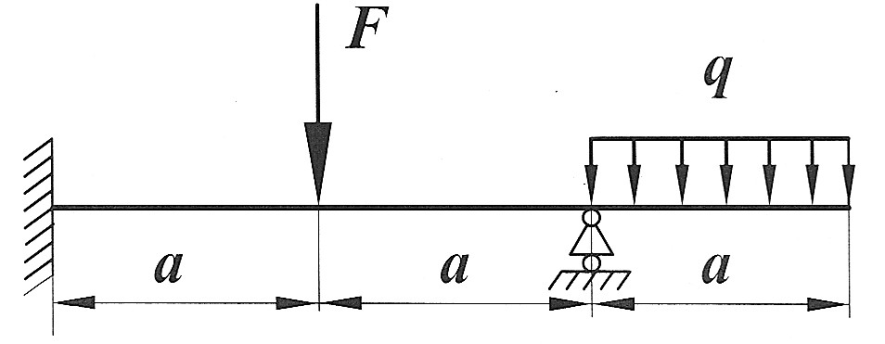
|
Раскрыть статическую неопределимость, построить эпюры 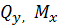 изображенной на рисунке балки. изображенной на рисунке балки.
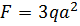 , ,

|
Задача 6
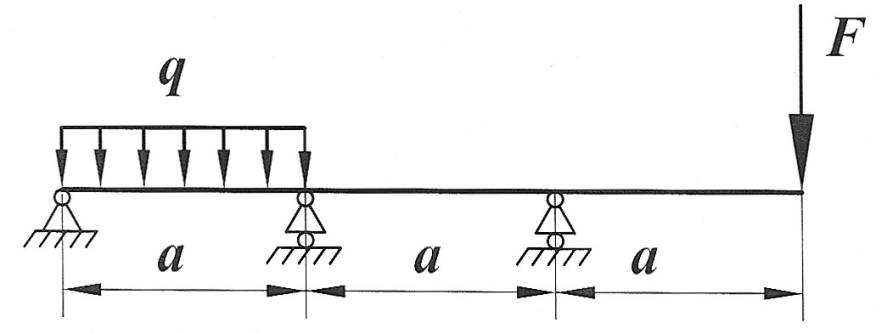
|
Раскрыть статическую неопределимость, построить эпюры 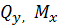 изображенной на рисунке балки. изображенной на рисунке балки.
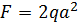 , ,

|
Задача 7
Раскрыть статическую неопределимость, построить эпюры 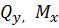 . Составить условие прочности. . Составить условие прочности.
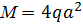 , ,

|
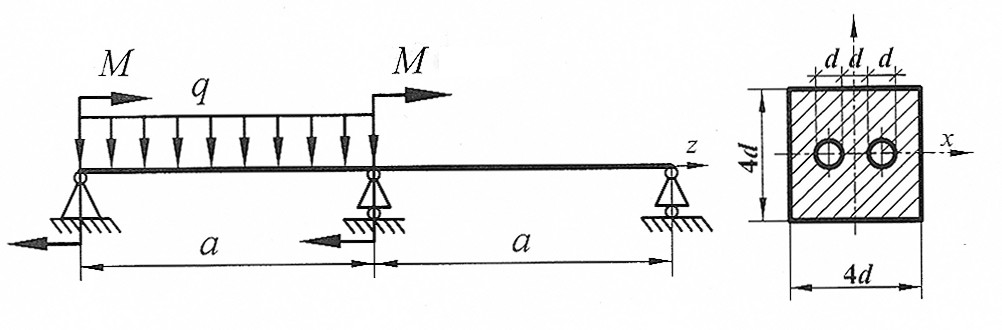
|
Задача 8
Раскрыть статическую неопределимость, построить эпюры 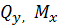 изображенной на рисунке балки. Составить условие прочности. изображенной на рисунке балки. Составить условие прочности.
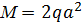 , ,

|
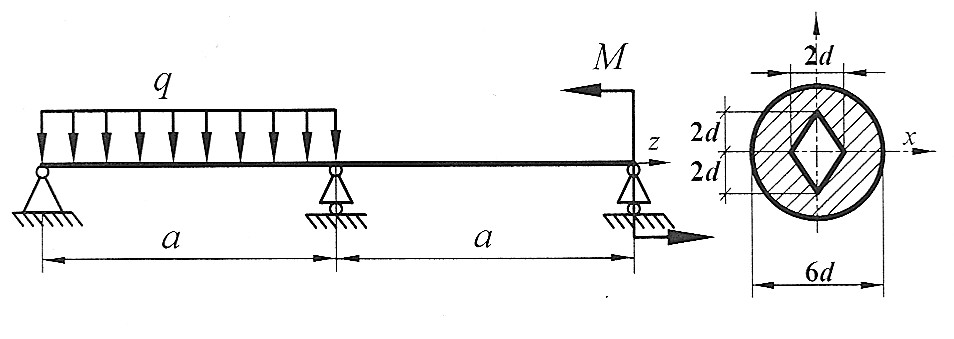
|
Задача 9
Раскрыть статическую неопределимость, построить эпюры 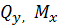 изображенной на рисунке балки. Составить условие прочности. изображенной на рисунке балки. Составить условие прочности.
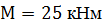 , ,
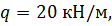
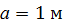 , ,

|

|
Задача 10
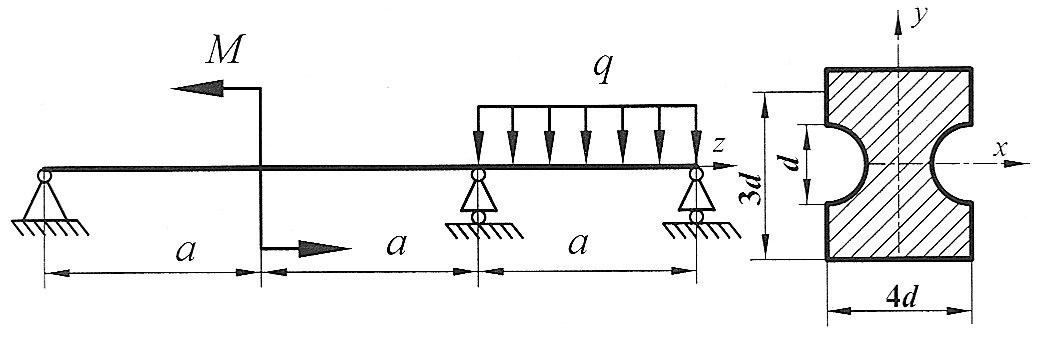
|
Раскрыть статическую неопределимость, построить эпюры 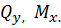 Составить условие прочности. Составить условие прочности.
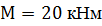 , ,
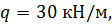
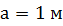 , , 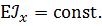
|
Задача 11
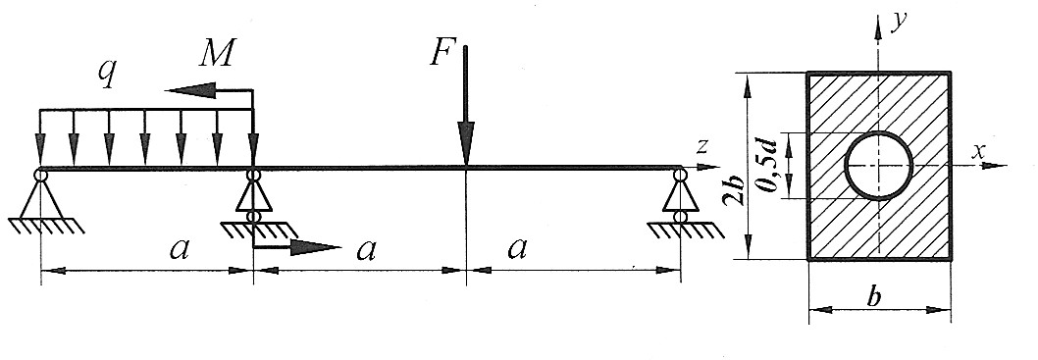
|
Раскрыть статическую неопределимость, построить эпюры 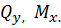 Составить условие прочности. Составить условие прочности.
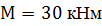 , ,
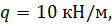
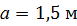 , , 
|
Задача 12

|
Раскрыть статическую неопределимость, построить эпюры 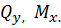 Составить условие прочности. Составить условие прочности.
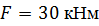 , ,
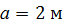 , ,

|
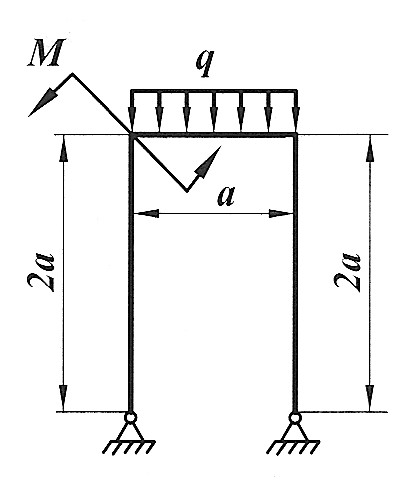
Задача 13
Раскрыть статическую неопределимость, построить эпюры 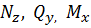 изображенной на рисунке рамы. изображенной на рисунке рамы.
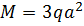 , ,

| 
|
Задача 14
Раскрыть статическую неопределимость, построить эпюры 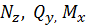 изображенной на рисунке рамы. изображенной на рисунке рамы.
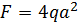 , ,

|
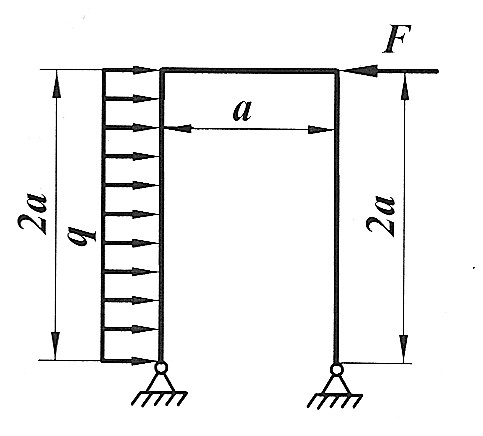
|
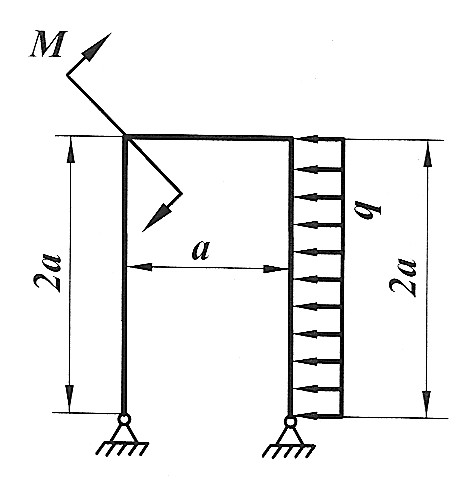
Задача 15
Раскрыть статическую неопределимость, построить эпюры 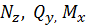 изображенной на рисунке рамы. изображенной на рисунке рамы.
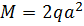 , ,

| 
|
Задача 16
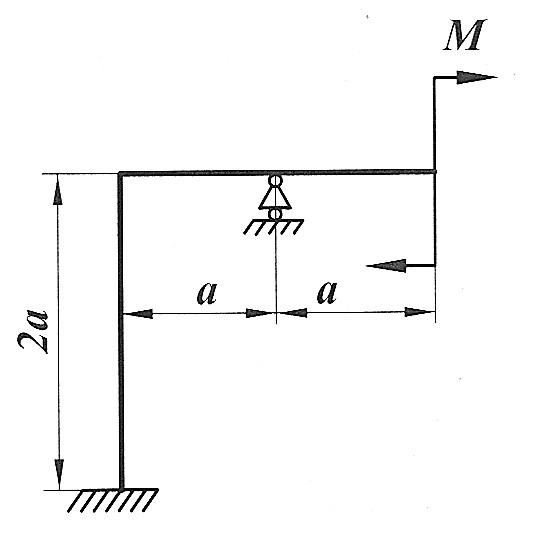
|
Раскрыть статическую неопределимость, построить эпюры 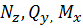 изображенной на рисунке рамы. изображенной на рисунке рамы.
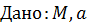 , ,

|
Задача 17
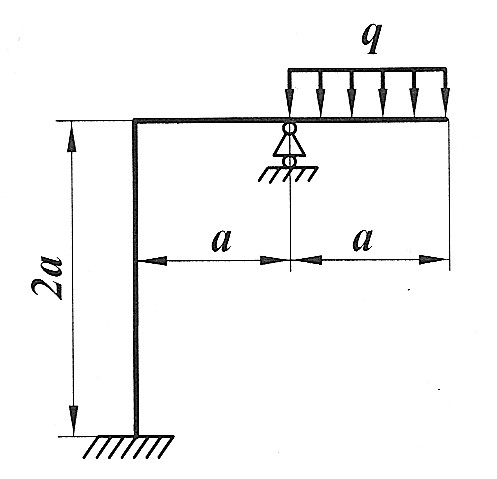
| Раскрыть статическую неопределимость, построить эпюры 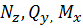 изображенной на рисунке рамы. изображенной на рисунке рамы.
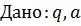 , ,

|
Задача 18
| Раскрыть статическую неопределимость, построить эпюры 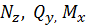 изображенной на рисунке рамы. изображенной на рисунке рамы.
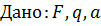 , ,

|
Задача 1 9
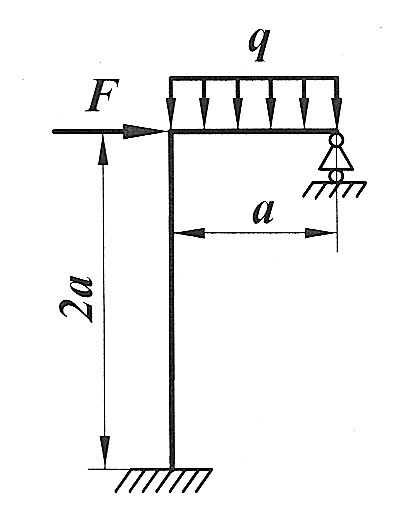
Раскрыть статическую неопределимость, построить эпюры 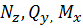 изображенной на рисунке рамы.
Из условия прочности определить размеры поперечного сечения. Найти горизонтальное перемещение сечения С и угол поворота сечения D изображенной на рисунке рамы.
Из условия прочности определить размеры поперечного сечения. Найти горизонтальное перемещение сечения С и угол поворота сечения D
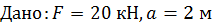 , , 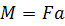 , , 

| 
|
Задача 20
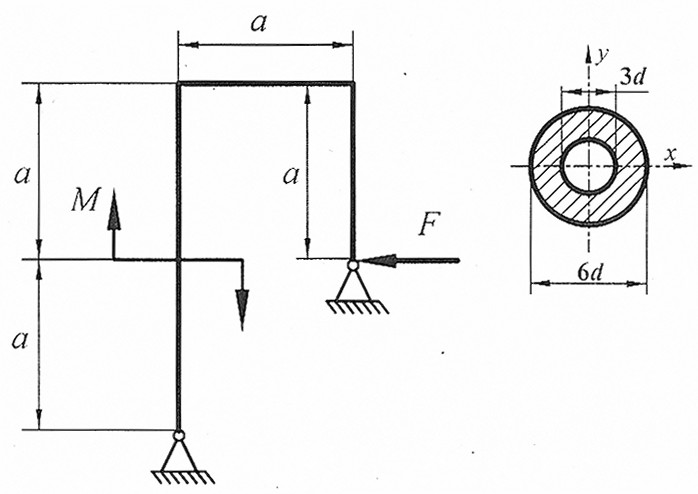
Раскрыть статическую неопределимость, построить эпюры 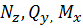 изображенной на рисунке рамы.
Составить условие прочности. изображенной на рисунке рамы.
Составить условие прочности.
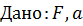 , , 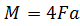 , d . , d .

| 
|
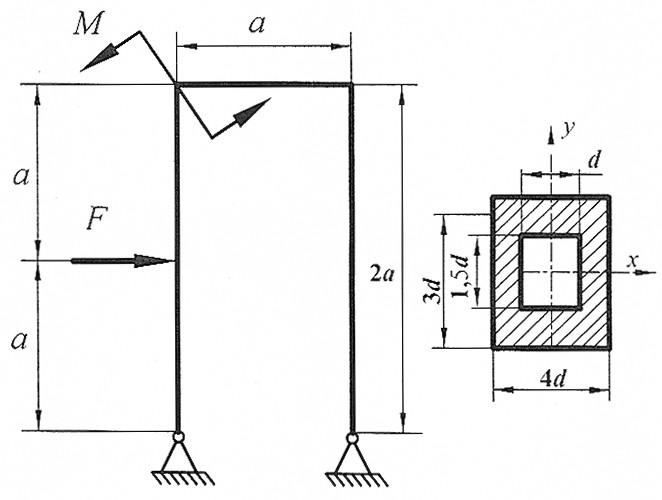
Задача 21
Раскрыть статическую неопределимость, построить эпюры 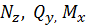 изображенной на рисунке рамы.
Составить условие прочности. изображенной на рисунке рамы.
Составить условие прочности.
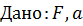 , , 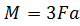 , d . , d .

| 
|
Задача 22
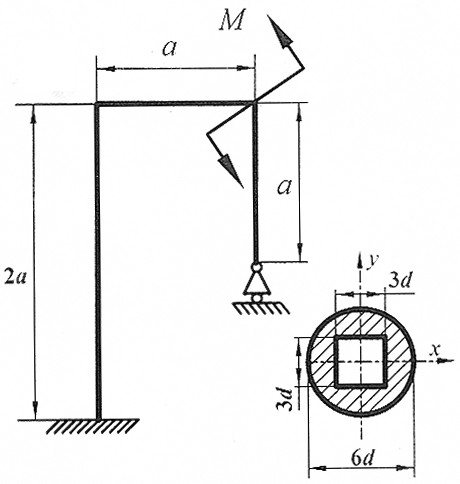
| Раскрыть статическую неопределимость, построить эпюры 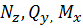 изображенной на рисунке рамы.
Составить условие прочности. изображенной на рисунке рамы.
Составить условие прочности.
 , ,
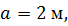 d = 2 см. d = 2 см.

|
Задача 2 3
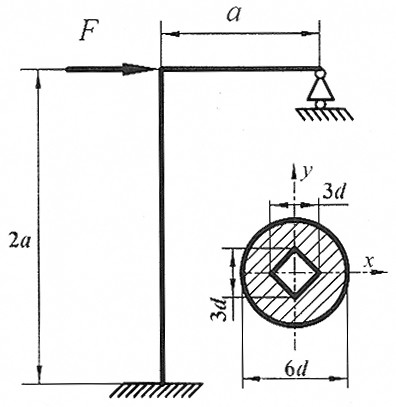
|
Раскрыть статическую неопределимость, построить эпюры 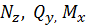 изображенной на рисунке рамы.
Составить условие прочности. изображенной на рисунке рамы.
Составить условие прочности.
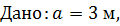 d = 3 см. d = 3 см.

|
Задача 2 4
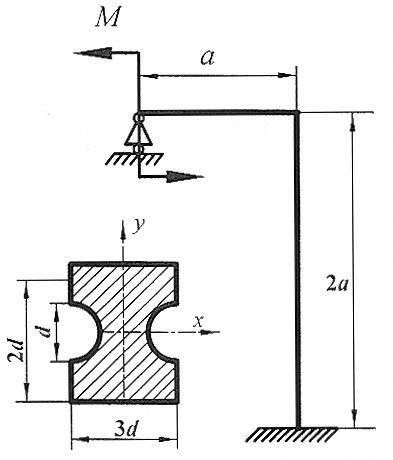
| Раскрыть статическую неопределимость, построить эпюры 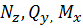 изображенной на рисунке рамы.
Составить условие прочности. изображенной на рисунке рамы.
Составить условие прочности.
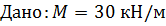 , , 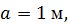 d = 3 см. d = 3 см.

|
Задача 25
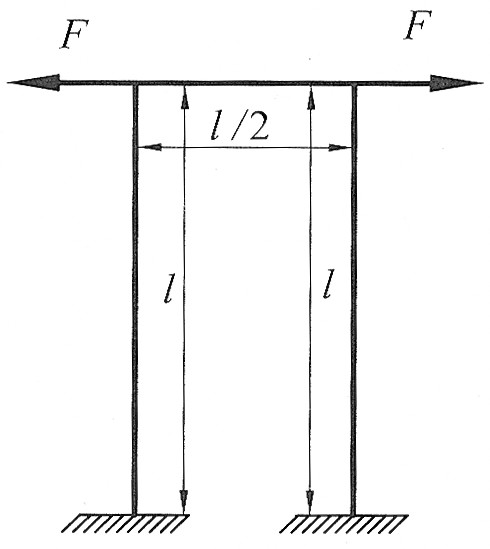
Раскрыть статическую неопределимость, построить эпюру изгибающих моментов изображенной на рисунке рамы.
Дано: 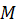 , , 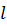 . .

| 
|
Задача 2 6
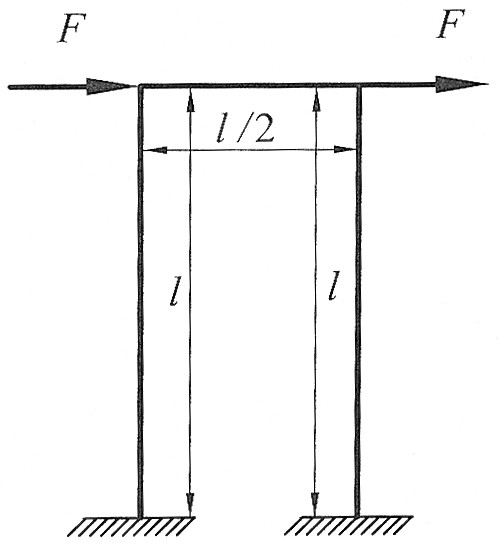
Раскрыть статическую неопределимость, построить эпюру изгибающих моментов изображенной на рисунке рамы.
Дано: 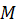 , , 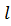 . .

| 
|
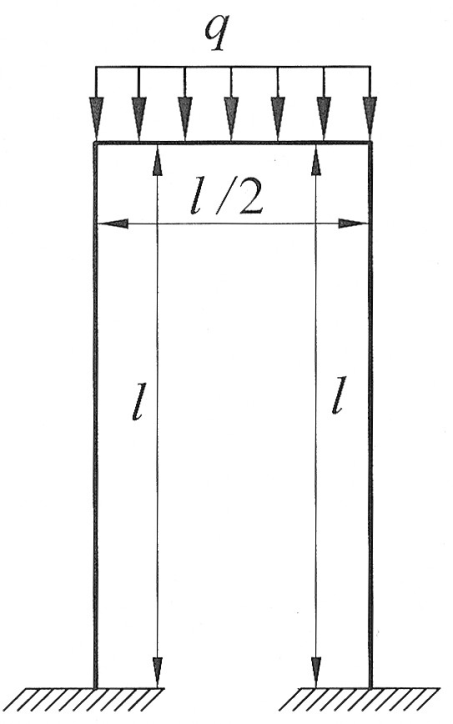
Задача 2 7
Раскрыть статическую неопределимость, построить эпюру изгибающих моментов изображенной на рисунке рамы.
Дано: 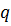 , , 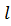 . .

| 
|
Задача 2 8
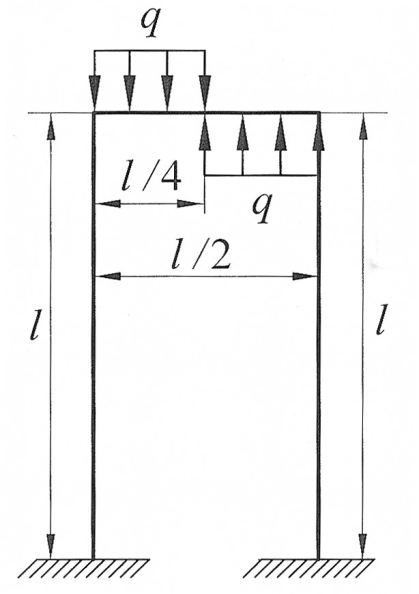
| Раскрыть статическую неопределимость, построить эпюру изгибающих моментов изображенной на рисунке рамы.
Дано: 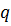 , , 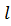 . .

|
Задача 29
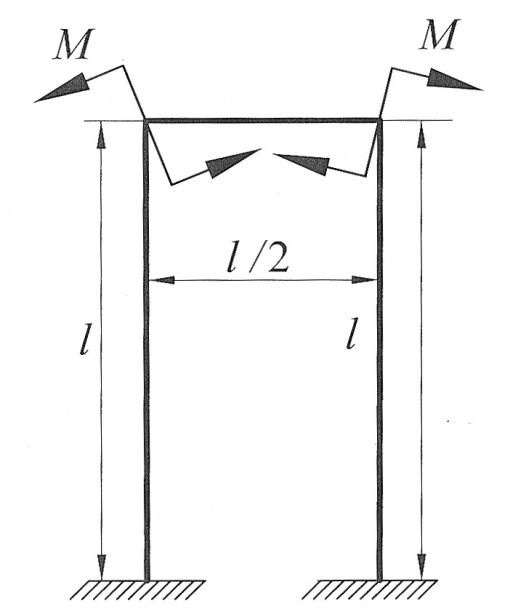
| Раскрыть статическую неопределимость, построить эпюру изгибающих моментов изображенной на рисунке рамы.
Дано: 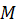 , , 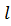 . .

|
Задача 30

| Раскрыть статическую неопределимость, построить эпюру изгибающих моментов изображенной на рисунке рамы.
Дано: 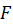 , , 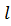 . .

|
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие деформации и перемещения возникают в балках, работающих на изгиб?
2. В чем состоит общая идея метода начальных параметров? Запишите универсальные уравнения для определения прогибов и углов поворота.
3. С помощью каких дифференциальных уравнений определяются перемещения при изгибе балок?
4. Какие методы используются для определения перемещений при изгибе балок?
5. Сколько неизвестных содержит выражение для прогибов при использовании метода начальных параметров
6. Какие типы опор применяются для соединения балок с основанием и какие реактивные усилия и моменты могут возникать в этих опорах?
7. Какие уравнения равновесия применяются для определения опорных реакций и как проверить правильность определения опорных реакций?
8. В каких случаях нельзя использовать универсальные уравнения метода начальных параметров для определения перемещений в балках?
9. Эпюры каких внутренних усилий используются при определении перемещений при изгибе методом Мора?
10. Какой физический смысл интегралов Мора?
11. Как выбираются направления действия единичных силы или момента при использовании метода Мора? Как определяется знак перемещений?
12. Укажите какие трудности можно отнести к недостаткам определения перемещений при помощи интеграла Мора?
13. Как можно вычислить интегралы Мора при определении перемещений в прямых стержнях с постоянной жёсткостью?
14. Для каких балок вместо непосредственного вычисления интеграла Мора можно использовать графоаналитический прием вычисления по правилу Верещагина?
15. В каком случае при вычислении интегралов Мора нельзя использовать правило А.К.Верещагина?
16. На какие простые фигуры можно разбить эпюры изгибающих моментов, построенных от внешней нагрузки, представляющих собой:
16.1.”однозначную” трапецию-трапецию, расположенную по одну сторону от нулевой оси;
16.2. “разнозначную” трапецию-трапецию, расположенную по обе стороны от нулевой оси;
16.3. “однозначную” трапецию, ограниченную сверху параболой;
16.4. “разнозначную” трапецию, ограниченную сверху параболой.
17. Какие системы называются статически неопределимыми?
18. Что называется степенью статической неопределимости?
19. Какая система называется геометрически неизменяемой?
20. Что представляет из себя основная и эквивалентная системы?
21. Что означают величины 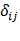 и
и 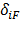 и как они определяются?
и как они определяются?
22. Напишите систему канонических уравнений?
23. Каким способом можно построить эпюры M, Q, N в заданной статически неопределимой системе после того, как определены неизвестные 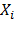 ?
?
24. На чем основана и как производится деформационная проверка суммарной эпюры изгибающих моментов?
25. Как производится определение перемещений в статически неопределимых системах?
ЗАКЛЮЧЕНИЕ
В методическом пособии кратко изложены теоретические основы определения перемещений, возникающих при изгибе балок и плоских стержневых систем по трем, наиболее широко используемым на практике, методам: методу начальных параметров, методу Мора, и способу Верещагина, а также их использование при раскрытии статической неопределимости методом сил. Для облегчения студентами применения правила «перемножения» эпюр по Верещагину приведены примеры разбиения сложных эпюр изгибающих моментов на простые фигуры с указанием положения центра их тяжести.
С целью лучшего усвоения студентами материала по каждому разделу разработан порядок решения задачи представлен подробный пример расчета.
Подробно рассмотрена задача по раскрытию статической неопределимости плоской стержневой системы (рамы) методом сил, а также особенности ее решения при использовании свойств симметрии.
В приложениях методического пособия приведены некоторые стандартные данные по определению геометрических характеристик плоских сечений (площади, осевых моментов инерции и сопротивления), а также таблицы прокатных профилей (двутавры, швеллеры) основных геометрических форм сечений стержней, используемых при проектировании инженерных конструкции.
По мнению авторов, данное методическое пособие может оказать студентам значительную помощь при изучении ими дисциплин «Сопротивление материалов» и «Техническая механика», а также при выполнении самостоятельных расчетных работ.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Феодосьев, В.И. Сопротивление материалов. – М.: Наука, 1999. – 560 с.
2. Беляев, Н.М. Сопротивление материалов. – М.: Наука, 1976. – 552 с.
3. Афанасьев, А.М. Лабораторный практикум по сопротивлению материалов / A.M. Афанасьев, В.А. Марьин. – М.: Наука, 1975. – 269 с.
4. Копнов, В.А. Сопротивление материалов: Руководство для решения задач и выполнения лабораторных и расчетно-графических работ / В.А. Копнов, С.Н. Кривошапко. – М.: Высш. шк., 2009. – 351 с.
5. Дарков, А.В. Сопротивление материалов / А.В. Дарков, Г.С. Шпиро. – М.: Высшая школа, 1984.
6. Макаров, Е.Г. Сопротивление материалов на базе Mathcad. – СПб.: БХВ-Петербург, 2004. – 512 с.
7. Александров А.В. Сопротивление материалов: / А.В. Александров, В.Д. Потапов, Б.П. Державин. – 2-е изд., испр. – М.: Высш. шк., 2000. – 560 с.
Приложение А. Двутавры стальные горячекатаные
Сортамент по ГОСТ 8239–89
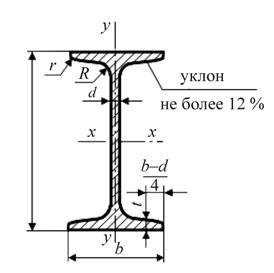
Номер балки
h
b
d
t
Площадь сечения, см2
Масса
1 м, кг
Номер балки
h
b
d
t
Площадь сечения, см2
Масса 1 м, кг
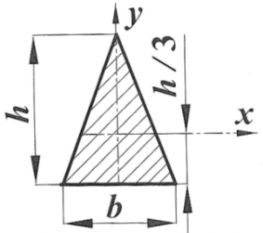
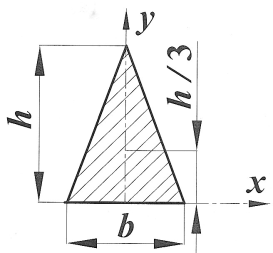
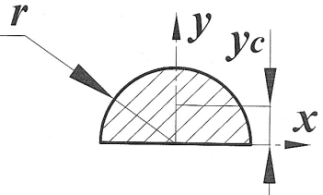
Приложение В. Площади, координаты центров тяжести
для основных форм сечений
| Сечение | Ордината центра тяжести yc | Площадь A |
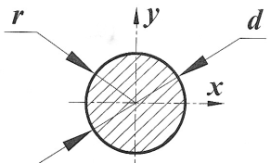
| 0 | 
|
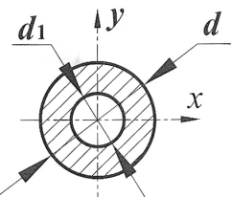
| 0 | 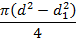
|
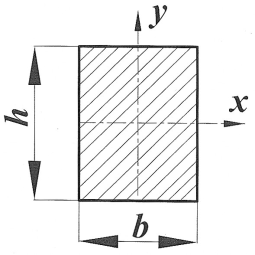
| 0 | bh |
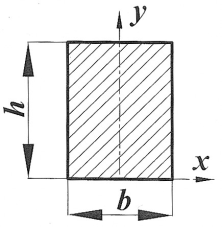
| 
| bh |
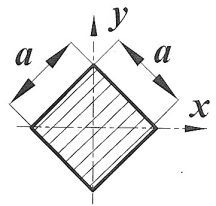
| 0 | 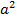
|
| 0 | 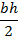
|
| 
| 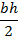
|
| 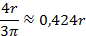
| 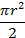
|
Приложение Г. Моменты инерции, моменты сопротивления
Приложение Д . Радиусы инерции для основных форм сечений
| Сечение | Радиус инерции ix | |

|
| |

|
| |

|
| |

|
| |

|
| |

|
| |

|
| |

|
| |
Учебное издание
И.С. Шеронина, С.А. Петерсон, А.С. Нефедов
МЕТОДЫ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ
В СТЕРЖНЕВЫХ СИСТЕМАХ
Редактор Л.С. Кокина
План 2018
Подписано в печать 27.04.2018. Формат 60х84 1/16. Бумага белая.
Печать ризограф. Усл. печ. л. 5,35. Уч.-изд. л. 5,33. Тираж . Заказ
Ярославский государственный технический университет
150023, Ярославль, Московский пр., 88
Издательский дом ЯГТУ
150000, Ярославль, ул. Советская, 14а
И.С. Шеронина, С.А. Петерсон,
А.С. Нефедов
МЕТОДЫ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ
В СТЕРЖНЕВЫХ СИСТЕМАХ
Ярославль
2018
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Ярославский государственный технический университет»
И.С. Шеронина, С.А. Петерсон, А.С. Нефедов
МЕТОДЫ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ
В СТЕРЖНЕВЫХ СИСТЕМАХ
Рекомендовано
научно-методическим советом университета
в качестве учебного пособия
Ярославль
Издательский дом ЯГТУ
2018
УДК 539
ББК 38.112
Ш49
Шеронина, И.С.
Ш49 Методы определения перемещений в стержневых системах: учебное пособие / И.С. Шеронина, С.А. Петерсон, А.С. Нефедов. – Ярославль: Издат. дом ЯГТУ, 2018. – 92 с.
ISBN
Учебное пособие разработано по курсам «Сопротивление материалов» и «Техническая механика» в соответствии с государственным общеобразовательным стандартом высшего профессионального образования. В работе изложены основные теоретические положения по темам «Методы определения перемещений при изгибе в стержневых системах» и «Статически неопределимые системы». Приведены примеры решения типовых задач по данным темам и предложены задачи для самостоятельного решения с целью проверки степени усвоения материала данных тем.
Рекомендовано для студентов механических и строительных направлений очной и заочной формы обучения.
Рецензенты: АО Ярижком (А.Ю. Юдин, канд. техн. наук, зам. директора); В.П. Панченко, канд. техн. наук, директор по науке и внедрению новых технологий ООО «СОТпрофи».
_____________________________________________________
Редактор Л.С. Кокина
План 2018
Подписано в печать 27.04.2018. Формат 60х84 1/16. Бумага белая.
Печать ризограф. Усл. печ. л. 5,35. Уч.-изд. л. 5,33. Тираж . Заказ
Ярославский государственный технический университет
150023, Ярославль, Московский пр., 88
Издательский дом ЯГТУ
150000, Ярославль, ул. Советская, 14а
_____________________________________________________
| ISBN | Ярославский государственный технический университет, 2018 |
Оглавление
| ВВЕДЕНИЕ.................................................................................................. | 5 |
| 1. МЕТОД НАЧАЛЬНЫХ ПАРАМЕТРОВ.......................................... | 6 |
| 1.1. Перемещение при изгибе. Универсальное уравнение упругой линии балки........................................................................... | 6 |
| 1.2. Порядок определения перемещений при изгибе по методу начальных параметров........................................................ | 9 |
| 1.3. Примеры определения перемещений при изгибе по методу начальных параметров. .................................................... | 9 |
| 2. МЕТОД МОРА................................................................................. | 12 |
| 2.1. Основные положения............................................................. | 12 |
| 2.2. Порядок определения перемещений при изгибе по методу Мора....................................................................................... | 13 |
| 2.3. Пример определения перемещений по методу Мора......... | 14 |
| 3. МЕТОД (ПРАВИЛО) ВЕРЕЩАГИНА.......................................... | 19 |
| 3.1. Основные положения правила Верещагина......................... | 19 |
| 3.2. Порядок определения перемещений по правилу Верещагина................................................................................... | 22 |
3.3. Примеры разбиения сложных площадей 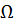 фигур
изгибающих моментов от внешней нагрузки и
вычисления произведения фигур
изгибающих моментов от внешней нагрузки и
вычисления произведения 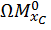 для случаев, в которых
единичная эпюра трапеция.......................................................... для случаев, в которых
единичная эпюра трапеция..........................................................
| 23 |
| 3.4. Пример определения перемещений по правилу Верещагина………………………………………………........... | 29 |
| 4. ЗАДАЧИ ДЛЯ ПРОВЕРКИ СТУДЕНТАМИ СТЕПЕНИ УСВОЕНИЯ МАТЕРИАЛА РАЗДЕЛА «ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ПРИ ИЗГИБЕ»…………………………………. | 33 |
| 5. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ПРИ ИЗГИБЕ……………………………………………………………… | 43 |
| 5.1. Основные положения…………………………………….. | 43 |
| 5.2. Порядок расчета статически неопределимых систем (рам, многопролетных балок)………………………………... | 45 |
| 5.3. Пример расчета статически неопределимой балки…….. | 46 |
| 5.4. Пример расчета статически неопределимой рамы……... | 53 |
| 5.5. Использование свойств симметрии при раскрытии статической неопределимости……………………………...... | 65 |
| 5.6. Пример расчета симметричной статически неопределимой рамы, нагруженной кососимметричной нагрузкой…………………………………………………......... | 67 |
| 6. ЗАДАЧИ ДЛЯ ПРОВЕРКИ СТУДЕНТАМИ СТЕПЕНИ УСВОЕНИЯ МАТЕРИАЛА РАЗДЕЛА «СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ | 75 |
| Контрольные вопросы......................................................................... | 85 |
| Заключение........................................................................................... | 86 |
| Библиографический список........................................................................ | 87 |
| Приложение А. Двутавры стальные горячекатаные. Сортамент по ГОСТ 8239–89..................................................................... | 88 |
| Приложение Б. Швеллеры стальные горячекатаные. Сортамент по ГОСТ 8240–89..................................................................... | 89 |
| Приложение В. Площади, координаты центров тяжести для основных форм сечений....................................................................... | 90 |
| Приложение Г. Моменты инерции, моменты сопротивления для основных форм сечений....................................................................... | 91 |
| Приложение Д. Радиусы инерции для основных форм сечений............. | 92 |
ВВЕДЕНИЕ
Во многих случаях при проектировании элементов конструкций недостаточно оценки их прочности. На первый план может выходить требование обеспечения заданной жесткости.
Для проверки жесткости конструкции необходимо научиться определять максимальные перемещения и перемещения конкретных точек или сечений её элементов. Также умение определять перемещение требуется для раскрытия статической неопределимости.
В данном пособии представлены три наиболее широко используемых метода определения перемещений: метод начальных параметров, метод Мора, способ (правило) Верещагина. В работе рассмотрены основные теоретические положения этих методов. Предложены планы определения перемещений каждым методом. Подробно разобраны примеры решения задач по определению перемещений в элементах вида "балка", "рама". Предложены задачи для самостоятельного решения с целью проверки степени усвоения материала.
В пособии представлен один из основных методов раскрытия статической неопределимости – метод сил в канонической его трактовке. Также в работе студентам предложен план раскрытия статической неопределимости методом сил. Решены статически неопределимые задачи данным методом (статически неопределимая балка, статически неопределимая рама). В работе даны рекомендации по использованию свойств симметрии при раскрытии статической неопределимости и рассмотрен пример решения симметричной статически неопределимой рамы, нагруженной кососимметричной нагрузкой. Далее студентам предложены статически неопределимые задачи для самостоятельного решения.
Пособие предназначено для подготовки студентов к выполнению расчётно-проектировочных и лабораторных работ, к решению экзаменационных задач по представленным в работе темам.
МЕТОД НАЧАЛЬНЫХ ПАРАМЕТРОВ
Дата: 2019-03-05, просмотров: 578.