Начало формы

Конец формы

Ряды динамики — это ряды статистических показателей, характеризующих развитие явлений природы и общества во времени. Ряды динамики позволяют выявить закономерности развития изучаемых явлений.

Ряды динамики содержат два вида показателей:

1 показатели времени (годы, кварталы, месяцы и др.) или моменты времени (на начало года, на начало каждого месяца и т.п.);

2 показатели уровней ряда. Показатели уровней рядов динамики могут быть выражены абсолютными величинами (производство продукта в тоннах или рублях), относительными величинами (удельный вес городского населения в %) и средними величинами (средняя заработная плата работников отрасли по годам и т. п.).

Правильное построение рядов динамики предполагает выполнение ряда требований:

-все показатели ряда динамики должны быть научно обоснованными, достоверными;

-показатели ряда динамики должны быть сопоставимы по времени, т.е. должны быть исчислены за одинаковые периоды времени или на одинаковые даты;

-показатели ряда динамики должны быть сопоставимы по территории;

-показатели ряда динамики должны быть сопоставимы по содержанию, т.е. исчислены по единой методологии, одинаковым способом;

-показатели ряда динамики должны быть сопоставимы по кругу учитываемых хозяйств. Все показатели ряда динамики должны быть приведены в одних и тех же единицах измерения.

Статистические показатели могут характеризовать либо результаты изучаемого процесса за период времени, либо состояние изучаемого явления на определенный момент времени, т.е. показатели могут быть интервальными (периодическими) и моментными. Соответственно  ряды динамики могут быть интервальными или моментными. Моментные ряды динамики в свою очередь могут быть с равными и неравными промежутками времени.

При анализе рядов динамики рассчитываются следующие показатели:

Абсолютные приросты (Δy) показывают, на сколько единиц изменился последующий уровень ряда по сравнению с предыдущим (цепные абсолютные приросты) или по сравнению с начальным уровнем (базисные абсолютные приросты). Формулы расчета можно записать следующим образом:

При уменьшении абсолютных значений ряда будет соответственно "уменьшение", "снижение".

Коэффициент роста показывает, во сколько раз изменился уровень ряда по сравнению с предыдущим (цепные коэффициенты роста или снижения) или по сравнению с начальным уровнем (гр. базисные коэффициенты роста или снижения). Формулы расчета можно записать следующим образом:

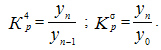
Темпы роста показывают, сколько процентов составляет последующий уровень ряда по сравнению с предыдущим (цепные темпы роста) или по сравнению с начальным уровнем (базисные темпы роста). Формулы расчета можно записать следующим образом:

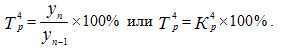
Темпы прироста показывают, на сколько процентов увеличился уровень отчетного периода по сравнению с предыдущим (цепные темпы прироста) или по сравнению с начальным уровнем (базисные темпы прироста). Формулы расчета можно записать следующим образом:

Т_пр = Т_р - 100%

 или Т_пр= абсолютный прирост / уровень предшествующего периода * 100%

Если абсолютные уровни в ряду уменьшаются, то темп будет меньше 100% и соответственно будет темп снижения (темп прироста со знаком минус).

Абсолютное значение 1% прироста показывает, сколько единиц надо произвести в данном периоде, чтобы уровень предыдущего периода возрос на 1 %. Определить величину абсолютного значения 1% прироста можно двумя способами:

§ уровень предшествующего периода разделить на 100;

§ цепные абсолютные приросты разделить на соответствующие цепные темпы прироста.

Абсолютное значение 1% прироста =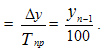

В динамике, особенно за длительный период, важен совместный анализ темпов прироста с содержанием каждого процента прироста или снижения.

Рассмотренная методика анализа рядов динамики применима как для рядов динамики, уровни которых выражены абсолютными величинами (т, тыс. руб., число работников и т.д.), так и для рядов динамики, уровни которых выражены относительными показателями (% брака, % зольности угля и др.) или средними величинами (средняя урожайность в ц/га, средняя заработная плата и т.п.).

Наряду с рассмотренными аналитическими показателями, исчисляемыми за каждый год в сравнении с предшествующим или начальным уровнем, при анализе рядов динамики необходимо исчислить средние за период аналитические показатели: средний уровень ряда, средний годовой абсолютный прирост (уменьшение) и средний годовой темп роста и темп прироста.

Методы расчета среднего уровня ряда динамики были рассмотрены выше. В рассматриваемом нами интервальном ряду динамики средний уровень ряда исчисляется по формуле средней арифметической простой:

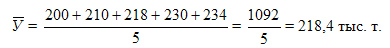
Среднегодовой объем производства продукта за 1994- 1998 гг. составил 218,4 тыс. т.

Среднегодовой абсолютный прирост исчисляется также по формуле средней арифметической простой:

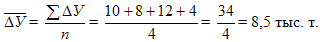
Ежегодные абсолютные приросты изменялись по годам от 4 до 12 тыс.т (см.гр.3), а среднегодовой прирост производства за период 1995 — 1998 гг. составил 8,5 тыс. т.

Методы расчета среднего темпа роста и среднего темпа прироста требуют более подробного рассмотрения. Рассмотрим их на примере приведенных в таблице годовых показателей уровня ряда.