1 Понятие стохастической связи и задачи корреляционного анализа

2 Регрессионный анализ

3 Использование методики парной корреляции  

4 Методика и этапы множественного корреляционного анализа

1 Понятие стохастической связи и задачи корреляционного анализа

На практике далеко не все экономические явления и процессы могут изучаться с помощью методики детерминированного факторного анализа, так как стохастические зависимости встречаются в экономических исследованиях гораздо чаще функциональных.

Математико-статистические методы изучения связей, называемые иначе стохастическим моделированием, являются в определенной степени дополнением и углублением детерминированного анализа. В анализе финансово-хозяйственной деятельности стохастические модели используются, когда необходимо:

-оценить влияние факторов, по которым нельзя построить жестко детерминированную модель;

-изучить и сравнить влияние факторов, которые невозможно включить в одну и ту же детерминированную модель;

-выделить и оценить влияние сложных факторов, которые не могут быть выражены одним определенным количественным показателем.

В отличие от детерминистского, стохастический подход для своей реализации требует выполнения ряда предпосылок. В первую очередь речь идет о наличии достаточно большой совокупности объектов (жестко детерминированную модель можно анализировать и строить по одному объекту, для стохастической же модели необходима совокупность). Кроме того, необходим достаточный объем наблюдений: по одному-двум наблюдениям судить о характере стохастической связи нельзя.

Использование стохастических моделей в экономике, в отличие от использования их в технике, имеет определенные трудности, связанные с получением совокупности достаточного объема. В технике эксперимент можно повторить, в экономике этого сделать нельзя. Это приводит к дискуссии о правомерности использования статистических методов при построении факторных моделей в анализе деятельности предприятий, поскольку при этом нередко приходится работать в условиях малых выборок (менее 20 наблюдений), а кроме того, в теории статистики считается, что при построении регрессии количество наблюдений должно в 6-8 раз превышать количество факторов, что крайне редко встречается в анализе финансово-хозяйственной деятельности предприятий.

Стохастические зависимости отличаются неопределенностью, приблизительностью: при них каждой величине факторного показателя (аргумента) может соответствовать несколько значений результативного показателя (функции). Корреляционная (стохастическая) связь – это неполная, вероятностная зависимость между показателями, которая проявляется только в сумме наблюдений, то есть связь между факторами и результативным показателем проявляется только при большом количестве наблюдений, когда по закону больших чисел влияние других факторов сглаживается, нейтрализуется.

Поскольку стохастическая модель - это, как правило, уравнение регрессии, при ее построении должны выполняться следующие условия:

-случайность наблюдений;

-наличие однородности совокупности, как качественной, так и количественной (показателем количественной однородности совокупности данных является показатель вариации, который мы рассмотрели в разделе 2.7.3);

-наличие специального математического аппарата (например, инструменты анализа автокорреляций для анализа рядов динамики).

Корреляционный анализ есть метод установления связи и измерения ее тесноты между наблюдениями, которые можно считать случайными и выбранными из совокупности, распределенной по многомерному нормальному закону.

Корреляционной связью называется такая статистическая связь, при которой различным значениям одной переменной соответствуют разные средние значения другой. Возникать корреляционная связь может несколькими путями. Важнейший из них - причинная зависимость вариации результативного признака от изменения факторного. Кроме того, такой вид связи может наблюдаться между двумя следствиями одной причины. Основной особенностью корреляционного анализа следует признать то, что он устанавливает лишь факт наличия связи и степень ее тесноты, не вскрывая ее причин.

Корреляционная связь может быть парная и множественная. Парная корреляция- это связь между двумя показателями, один из которых является факторным, другой - результативным. Множественная корреляция - это связь нескольких факторов с результативным показателем.

Для исследования стохастических зависимостей могут быть применены следующие приемы экономического анализа: сравнение параллельных и динамических рядов, аналитические группировки, графики- эти приемы позволяют определить общий характер и направление связи. Для определения степени влияния каждого фактора на результативный показатель применяются способы корреляционного, регрессионного дисперсионного, компонентного, современного многомерного факторного анализа. Наиболее широко при стохастических зависимостях применяются корреляционный способ. При этом необходимыми условиями его применения являются следующие:

1 Массовость значений изучаемых показателей, то есть наличие достаточно большого количества наблюдений о величине исследуемых факторных и результативных показателей (в динамике или за отчетный год по совокупности однородных объектов). Форма взаимосвязи между факторами и результативным показателем выявляется только тогда, когда для исследования используется большое количество наблюдений.

2 Исследуемые факторы должны иметь количественное измерение и отражаться в тех или иных источниках информации.

Основная сфера приложения стохастических моделей — это проблемно-ориентированный и тематический анализ. Корреляционный анализ направлен на решение следующих задач:

1 -установление самого факта наличия (или отсутствия) статистически значимой связи между изучаемыми признаками;

2 установление тесноты связи между факторами и результативным показателем;

3 оценка влияния факторов на величину результативного показателя.

Теснота связи между явлениями измеряется корреляционным отношением с помощью различных коэффициентов (коэффициент корреляции).

В статистике теснота связи может определяться с помощью различных коэффициентов (Фехнера, Пирсона, коэффициента ассоциации и т.д.), а в анализе хозяйственной деятельности чаще используется линейный коэффициент корреляции.

Коэффициент корреляции между факторами x и у определяется следующим образом:

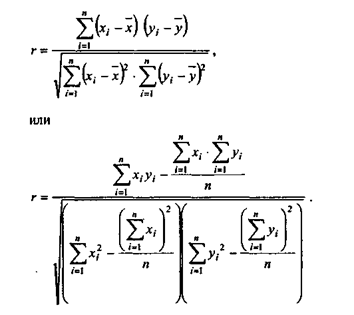
Таким же образом вычисляется коэффициент корреляции между факторами в двухфакторной регрессионной модели вида у = ах + b, a также при любой другой форме связи между двумя показателями.

Значения коэффициента корреляции изменяются в интервале [-1; + 1]. Значение r = -1 свидетельствует о наличии жестко детерминированной обратно пропорциональной связи между факторами, r = +1 соответствует жестко детерминированной связи с прямо пропорциональной зависимостью факторов. Если линейной связи между факторами не наблюдается, r 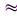0. Другие значения коэффициента корреляции свидетельствуют о наличии стохастической связи, причем чем ближе |r| к единице, тем связь теснее.

При |r|<0,3 связь можно считать слабой; при 0,3 < |r| < 0,7 - связь средней тесноты; |r| > 0,7 - тесная. Существуют и более дробные градации (например, таблица Чэддока).

Практическая реализация корреляционного анализа включает следующие этапы:

а) постановка задачи и выбор признаков;

б) сбор информации и ее первичная обработка (группировки, исключение аномальных наблюдений, проверка нормальности одномерного распределения);

в) предварительная характеристика взаимосвязей (аналитические группировки, графики);

г) устранение мультиколлинеарности (взаимозависимости факторов) и уточнение набора показателей путем расчета парных коэффициентов корреляции;

д) исследование факторной зависимости и проверка ее значимости;

е) оценка результатов анализа и подготовка рекомендаций по их практическому использованию.

Использование корреляционного анализа значительно углубляет факторный анализ и знания об изучаемом явлении, определяет закономерности его развития, устанавливает место и роль каждого фактора в формировании результативных показателей, на основе чего более точно разрабатываются и обосновываются планы и управленческие решения, более объективно оцениваются итоги хозяйственной деятельности предприятий и более полно определяются внутрихозяйственные резервы.

Регрессионный анализ

С корреляционным анализом тесно связан регрессионный анализ - это метод установления аналитического выражения стохастической зависимости между исследуемыми признаками.

Уравнение регрессии показывает, как в среднем изменяется у при изменении любого из x_i, и имеет вид:

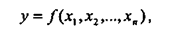
где у - зависимая переменная (она всегда одна);

х_i - независимые переменные (факторы) (их может быть несколько).

Если независимая переменная одна - это простой регрессионный анализ. Если же их несколько (п 2), то такой анализ называется многофакторным.

В ходе регрессионного анализа решаются две основные задачи:

-построение уравнения регрессии, т.е. нахождение вида зависимости между результатным показателем и независимыми факторами x₁, x₂, …, x_n.

- оценка значимости полученного уравнения, т.е. определение того, насколько выбранные факторные признаки объясняют вариацию признака у.

Применяется регрессионный анализ главным образом для планирования, а также для разработки нормативной базы.

В отличие от корреляционного анализа, который только отвечает на вопрос, существует ли связь между анализируемыми признаками, регрессионный анализ дает и ее формализованное выражение. Кроме того, если корреляционный анализ изучает любую взаимосвязь факторов, то регрессионный - одностороннюю зависимость, т.е. связь, показывающую, каким образом изменение факторных признаков влияет на признак результативный.

Регрессионный анализ - один из наиболее разработанных методов математической статистики. Для реализации регрессионного анализа необходимо выполнение ряда специальных требований (в частности, x_l,x₂,...,x_n; y должны быть независимыми, нормально распределенными случайными величинами с постоянными дисперсиями). В реальной жизни строгое соответствие требованиям регрессионного и корреляционного анализа встречается очень редко, однако оба эти метода весьма распространены в экономических исследованиях. Зависимости в экономике могут быть не только прямыми, но и обратными и нелинейными. Регрессионная модель может быть построена при наличии любой зависимости, однако в многофакторном анализе используют только линейные модели вида:

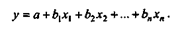
Построение уравнения регрессии осуществляется, как правило, методом наименьших квадратов, суть которого состоит в минимизации суммы квадратов отклонений фактических значений результатного признака от его расчетных значений, т.е.:

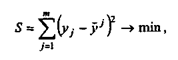
где т - число наблюдений;

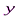^j = a + b₁x₁^j + b₂x₂^j+ ... + b_nх_n^j - расчетное значение результатного фактора.

Коэффициенты регрессии рекомендуется определять с помощью аналитических пакетов для персонального компьютера или специального финансового калькулятора. В наиболее простом случае коэффициенты регрессии однофакторного линейного уравнения регрессии вида y = а + bх можно найти по формулам:

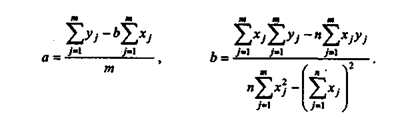
   3  Использование методики парной корреляции

Алгоритм расчетов при корреляционном анализе связи парной корреляции состоит из следующих этапов:

1 Проводится отбор наиболее важных факторов, влияющих на результативный показатель, с учетом причинно-следственных связей между показателями. При этом все факторы должны быть количественно измеримы. Отбор показателей для анализа и придание им статуса фактора или результативного показателя проводится на основе знания экономических законов.

2 Выбранные факторы наносятся на поле координат, то есть строится корреляционное поле.

3 Проводится обоснование формы связи: по форме корреляционного поля; путем визуального анализа ранжированного (в порядке возрастания или убывания) ряда факторов. Форма связи между показателями определяет дальнейшие действия корреляционного анализа. Например, если связь носит прямолинейный характер, то рассчитывается коэффициент корреляции, который дает количественную оценку тесноты связи.

4 Выбирается и решается уравнение регрессии.

   Наиболее простым уравнением, характеризующим прямолинейную зависимость между двумя показателями, являются уравнение прямой:

                                       Ух = а+bх

где, х - факторный показатель;

  У - результативный показатель;

  а, b - параметры уравнения регрессии, которые надо отыскать. Причем b - коэффициент регрессии несет основную смысловую нагрузку. Он показывает насколько единиц в среднем изменится результативный показатель (У) с изменением на одну единицу факторного признака (х). Эта величина на графике показывает угол наклона прямой. Свободный член а показывает начальную ординату, то есть расстояние от начала координат до пересечения прямой с осью У.

       Значения коэффициентов а и b находят способом наименьших квадратов. Он основан на предположении, что линия, выравнивающая эмпирические данные, должна проходить так, чтобы сумма квадратов отклонений от этой линии была наименьшей. Используя способов наименьших квадратов, первоначальное уравнение прямой примет следующий вид:

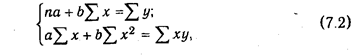
где п - количество наблюдений.

Однако, уравнения регрессии еще не дает ответа на вопрос: какова теснота связи между показателями, решающее или нет влияние оказывает фактор на результативный показатель. Для измерения тесноты связи между факторами и результативным показателем рассчитывается коэффициент корреляции. В случае прямолинейно связи коэффициент корреляции рассчитывается по формуле:

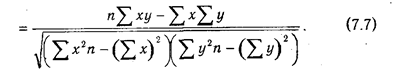
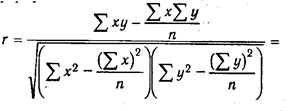
   Коэффициент корреляции может принимать значения от 0 до 1.

При r = 0, связь между показателями отсутствует;

если r = 1, связь функциональная (детерминированная);

если r<0, то связь между показателями обратная;

если r>0, то связь между показателями прямая.

      Чем ближе коэффициент корреляции к 1, тем более тесная связь между показателями. Теснота связи между показателями при различных значениях корреляционного соотношения представлена в таблице 2.

Таблица 2 Качественная оценка тесноты связи при различных значениях корреляционного соотношения.

        Если коэффициент корреляции возвести в квадрат: (0,66² = 0,435), то получим коэффициент детерминации (d), который показывает, на сколько процентов результативный показатель зависит от изучаемого фактора. (урожайность зерновых культур на 43,5 % зависит от качества почвы, а на 56,5 % от влияния других факторов.)