Все явления и процессы хозяйственной деятельности предприятий находятся во взаимосвязи и обусловленности. При этом каждое явления можно рассматривать как причину и следствие, как фактор и результат. Каждый результативный показатель зависит от большего числа разнообразных факторов, влияние которых можно изучить и измерить. И чем детальнее исследуется влияние факторов на результативный показатель, тем точнее результаты анализа и оценки качества работы предприятия. Экономический анализ – это, прежде всего, факторный анализ. Без подробного и комплексного изучения влияния факторов на результативные показатели нельзя сделать обоснованные выводы о результатах финансово-хозяйственной деятельности предприятия, обосновать и оценить выполнение планов, выявить неиспользованные внутрихозяйственные резервы и обосновать рациональные управленческие решения.
Детерминированный (функциональный) факторный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер, то есть когда результативный показатель представлен в виде алгебраической суммы, частного, произведения частных факторов. Функционально-детерминированная связь – это связь, при которой каждому значению факторного признака соответствует вполне определенное неслучайное значение результативного показателя.
Методика проведения факторного анализа предусматривает выполнение следующих этапов:
1 Отбор факторов, влияющих на исследуемые результативные показатели. При этом проводится как можно более подробная детализация факторов, учитываются их взаимосвязи, выделяются главные факторы.
2 Проведение классификации и систематизации факторов в целях обеспечения системного комплексного подхода к исследованию их влияния на результативные показатели. При этом классификация факторов предполагает распределение их по группам в зависимости от общих признаков. Систематизация факторов – это определение последовательности, очередности их анализа.
3 Определение формы зависимости между факторами и результативными показателями, то есть имеющаяся связь функциональная или стохастическая, прямая или обратная, прямолинейная или криволинейная. На этом этапе используется теоретический и практический опыт аналитика, а также способы сравнения динамических рядов, аналитические группировки и другие методы.
4 Моделирование взаимосвязи, то есть построение факторной модели между факторами и результативным показателем. Сущность моделирования заключается в том, что взаимосвязь исследуемого показателя с факторами передается в форме конкретного математического уравнения. При этом различают модели детерминированные и стохастические.
5 Определение влияния каждого из факторов и оценка этого влияния на изменение величины результативного показателя. Это один из основных этапов факторного анализа, для проведения которого применяются различные приемы и способы факторного анализа, которые мы подробно рассмотрим позже.
6 Практическое использование факторной модели, то есть подсчет резервов увеличения результативного показателя, планирование и прогнозирование его величины.
Моделирование взаимосвязей между показателями является одним из важнейших этапов факторного анализа. Моделирование - это один из важнейших методов научного познания, с помощью которого создается модель (условный образ) объекта исследования в виде формы конкретного математического уравнения. При этом моделирование их предусматривает выполнения ряда необходимых требований:
1 факторы, включаемые в модель, и сами модели должны быть реальными, а не выдуманными, абстрактными величинами;
2 факторы, которые входят в факторную модель, должны быть не только элементами формулы, но и находятся в причинно- следственной связи с изучаемыми показателями;
3 все показатели факторной модели должны быть количественно измеримы, то есть должны иметь единицу измерения и необходимую информационную обеспеченность;
4 факторная модель должна обеспечивать возможность измерения влияния отдельных факторов, то есть в ней должна учитываться соразмерность изменения факторов и результативного показателя, а сумма влияния отдельных факторов должна равняться общему изменению результативного показателя.
Детерминированные факторные модели могут быть разного типа: аддитивные, мультипликативные, кратные, смешанные.
Важным и сложным этапом факторного анализа является моделирование и преобразование факторных моделей, которое может осуществляться различными способами. Так, моделирование мультипликативных факторных моделей может осуществляться путем последовательного расчленения исходной факторной модели на факторы сомножители. Например, в рассмотренной выше модели валовой продукции годовая производительность труда может быть представлена как произведение отработанных дней одним работником (Д) и дневной производительности труда (ДП), которая в свою очередь определяется произведением продолжительности рабочего дня (П) на часовую производительность труда (ЧП). Моделирование факторной модели валовой продукции через трудовые факторы в этом случае будет иметь следующий вид:
ВП = Р х ГП = Р х Д х ДП = Р х Д х П х ЧП
Аналогично осуществляется моделирование аддитивных факторных моделей. Например, факторная модель выручки (В), которая зависит от производственных затрат (ПЗ) и прибыли (П), может быть преобразована в другую факторную модель, если разложить производственные затраты на сумму постоянных (ПЗс) и переменных производственных затрат (ПЗу) :
В = ПЗ + П = ПЗс + ПЗу + П
В детерминированном факторном анализе используются следующие основные приемы моделирования кратных факторных моделей:
1) Метод удлинения исходной факторной системы. Сущность метода заключается в разложении числителя кратной модели на составляющие его факторы с последующим получением развитой факторной модели аддитивного вида.
2) Метод формального разложения исходной факторной системы. Сущность этого метода заключается в разложении знаменателя исходной факторной системы кратного вида на составляющие его факторы с получением конечной факторной системы кратного аддитивного вида.
3) Метод расширения исходной факторной системы. Предполагает умножение и числителя, и знаменателя кратной модели на один и тот же фактор с последующим получением конечной факторной системы мультипликативного вида.
4) Метод сокращения исходной факторной системы. Предполагает числитель и знаменатель исходной факторной модели разделить на один и тот же показатель с получением развитой факторной системы того же кратного вида.
Задача детерминированного факторного анализа состоит в определении и количественном измерении влияния каждого из факторов на результативный показатель. При этом используются следующие способы детерминированного факторного анализа: цепные подстановки, способ абсолютных разниц, способ относительных разниц, индексный метод, интегральный метод, метод долевого участия, метод пропорционального деления и др.. Первые четыре способа основываются на методе элиминирования. Элиминировать - означает устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя кроме одного. Этот метод исходит из того, что все факторы изменяются независимо друг от друга: то есть сначала изменяется один фактор, а все другие остаются без изменения, потом меняются два фактора при неизменных остальных, затем три фактора и т.д. Это позволяет определить влияние каждого фактора на результативный показатель в отдельности.
Способ цепных подстановок. Наиболее универсальным из способов элиминирования является прием цепных подстановок. Он используется для расчета влияния факторов во всех типах детерминированных факторных моделей. Этот способ заключается в определении ряда промежуточных значений результативного показателя путем последовательной замены базисных факторов на отчетные. Разница промежуточных значений равна изменению результативного показателя за счет заменяемого фактора. Количество промежуточных значений на одну меньше количества факторов, влияющих на данный результативный показатель.
Преимуществом этого способа является его универсальность и простота применения. Однако этот метод имеет существенный недостаток: значение влияния факторов зависит от последовательности подстановки, так как в результате применения этого способа образуется неразложимый остаток, который прибавляется к величине влияния последнего фактора, поэтому в зависимости от выборочного порядка замены факторов результаты факторного анализа имеют разные значения. Но в практических расчетах точностью оценки влияния факторов пренебрегают, выдвигая на первый план относительную значимость влияния того или иного фактора. Существуют определенные правила, определяющие последовательность подстановки:
-при наличии в факторной модели количественных и качественных факторов в первую очередь производится подстановка количественных факторов;
-если модель представлена несколькими количественными и качественными факторами, то последовательность подстановки определяется путем логического анализа, то есть определяются первичные, вторичные количественные и качественные показатели.
Рассмотрим прием цепной подстановки на примере мультипликативной двухфакторной модели валовой продукции, рассчитанной через трудовые факторы:
ВП= Р х ГП
где, ВП - валовая продукция;
Р – численность рабочих;
ГП – годовая производительность труда.
Для определения влияния рассмотренных факторов на изменение валовой продукции в отчетном году (ВПо) по сравнению с базисным годом (ВПб) необходимо заменить на отчетный год сначала количественный фактор (численность рабочих), а затем качественный фактор (годовую производительность труда):
ВПб = Рб х ГПб
ВПусл = Ро х ГПб
ВПо = Ро х ГПо
Влияние на изменение валовой продукции количественного фактора (численности рабочих) определяется как разница между валовой продукцией условной и валовой продукцией базисной (ВПусл – ВПб). Влияние качественного фактора (годовой производительности труда) определяется как разница между валовой продукцией отчетной и валовой продукцией условной ( ВПо – ВПусл). Общее изменение валовой продукции за счет влияния двух факторов вместе определяется как разница между валовой продукцией отчетной и валовой продукцией базисной (ВПо – ВПб).
После расчета влияния факторов надо сделать проверку отклонений: общее изменение валовой продукции должно равняться алгебраической сумме отклонений в валовой продукции за счет влияния факторов:
∆ВП общее = ∆ВПр + ∆ВПгп
Способ абсолютных разниц является одной из модификаций приема элиминирования. Этот прием более простой, чем прием цепной подстановки, так как требует меньшего количества расчетов, но применять его можно только в мультипликативных и аддитивно-мультипликативных факторных моделях, то есть в кратных факторных моделях этот прием не применяется.
При использовании приема абсолютных разниц влияние факторов рассчитывается умножением абсолютного прироста исследуемого фактора на базовую величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в факторной модели.
В качестве примера применения приема абсолютных разниц, используем рассмотренную выше факторную модель валовой продукции через трудовые факторы:
ВП = Р х ГП
Используя прием абсолютных разниц, необходимо также учитывать место факторов в факторной модели, то есть сначала находим влияние количественного фактора, а затем качественного:
∆ВПр = ( Ро – Рб) х ГПб
∆ВПгп = (ГПо – ГПб) х Ро
∆ВП общее = ВПо – ВПб
Проверка: ∆ВПобщее = ∆ВПр + ∆ВПгп
Способ относительных разниц. Способ относительных разниц как и способ абсолютных разниц применяется только в мультипликативных и аддитивно- мультипликативных моделях. Этот способ значительно проще приема цепной подстановки и особенно эффективен, когда исходные данные уже содержат определенные ранее относительные приросты факторных показателей в % или коэффициентах.
В качестве примера используем рассмотренную выше факторную модель валовой продукции:
ВП = Р х ГП
Сначала надо определить относительные отклонения в факторных показателях:
Р% = Ро – Рб х 100
Рб
ГП% = ГПо – ГПб х 100%
ГПб
Затем рассчитаем влияние каждого фактора на изменение валовой продукции:
∆ВПр = ВПб х Р%
100
∆ВПгп = (ВПб + ВПр ) х ГП %
100
∆ВП общ = ВПo - ВПб
Проверка: ∆ ВПобщее = ∆ ВПр + ∆ВПгп
Интегральный метод. Рассмотренные выше традиционные способы факторного анализа основаны на методе элиминирования, недостатком которого является некоторая условность результатов расчетов, так как при этом способе образуется дополнительный прирост результативного показателя, который прибавляется к влиянию последнего фактора, в связи с чем, величина влияния факторов меняется с изменением места, на которое поставлен тот или иной фактор в детерминированной факторной модели. Чтобы избавиться от этого недостатка в детерминированных факторных моделях используется интегральный способ, который применяется для определения влияния факторов в мультипликативных, кратных и смешанных моделях кратно-аддитивного типа.
Использование интегрального способа позволяет получить более точные расчеты влияния факторов на результативный показатель по сравнению с другими рассмотренными ранее приемами. При использовании интегрального способа результаты расчетов не зависят от места факторов в факторной модели, а дополнительный прирост результативного показателя, который образуется от взаимодействия факторов, раскладывается между ними поровну. При использовании интегрального метода исчисление определенного интеграла по заданной подынтегральной функции и заданному интервалу интегрирования осуществляется по имеющейся стандартной программе с применением современных средств вычислительной техники.
Если мы осуществляем решение мультипликативной модели, то для расчета влияния отдельных факторов на обобщающий экономический показатель можно использовать следующие формулы:
Z=xy;
ΔZ(x) = y0 *Δx + 1/2Δx *Δy
Z(y)=x0 * Δy +1/2Δx * Δy
При решении кратной модели для расчета влияния факторов воспользуемся такими формулами:
Z=x /y;
ΔZ(x) = Δx/Δy Ln y1/y0
ΔZ(y)=ΔZ - ΔZ(x)
Рассмотрим применение интегрального метода на примере используемой ранее факторной модели валовой продукции:
ВП = Р х ГП
∆ ВПр = ( Ро – Рб) х ГПб + ((Ро – Рб)х (ГПо – ГПБ)) :2
∆ ВПгп = (ГПо – ГПб) х Рб + ((Ро – Рб) х ( ГПо – ГПб)) : 2
∆ВП общее = ВПо – ВПб
Кроме этого способа, в анализе находит применение также способ логарифмирования. Он используется при проведении факторного анализа, когда решаются мультипликативные модели. Сущность этого способа заключается в том, что при его использовании имеет место логарифмически пропорциональное распределение величины совместного действия факторов между последними, то есть эта величина распределяется между факторами пропорционально доле влияния каждого отдельного фактора на сумму обобщающего показателя. При интегральном же методе упомянутая величина распределяется между факторами в одинаковой мере. Поэтому метод логарифмирования делает расчеты влияния факторов более обоснованными по сравнению с интегральным методом.
В процессе логарифмирования используют не абсолютные величины прироста показателей, как это имеет место при интегральном методе, а относительные, то есть индексы изменения этих показателей. Например, обобщающий экономический показатель определяется в виде произведения двух факторов — сомножителей f = x y .
Найдем влияние каждого из этих факторов на обобщающий экономический показатель. Так, влияние первого фактора может быть определено по следующей формуле:
Δfx = Δf · lg(xо / xб) / lg(fо / fб)
Влияние второго фактора может быть определено по следующей формуле:
Δfy = Δf · lg(yо / yб) / lg(fо / fб)
Таким образом, общая сумма изменения обобщающего показателя распределяется между отдельными факторами в соответствии с пропорциями отношений логарифмов отдельных факторных индексов к логарифму обобщающего показателя.
Способы пропорционального деления и долевого участия
Способ пропорционального деления используют для аддитивных и кратно-аддитивных моделей.
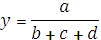
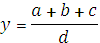
Суть способа пропорционального деления состоит в том, что необходимо общее изменение результативного показателя распределить пропорционально влиянию каждого фактора. Алгоритм расчета количественного влияния исследуемого фактора на изменение результативного показателя для аддитивной модели:
1 Абсолютное изменение результативного показателя делят на сумму абсолютных изменений всех факторов.
2 Полученный результат умножают на абсолютное отклонение исследуемого фактора.
Например: 
. Расчет будет проводиться следующим образом:
Изменение Y за счет фактора а:
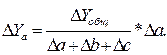
Изменение Y за счет фактора b:
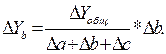
Изменение Y за счет фактора с:
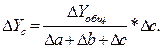
Сумма влияния факторов должна быть равна общему изменению результативного показателя.
Методика расчета для смешанных моделей несколько сложнее. Взаимосвязь факторов в комбинированной модели показана на рис. 6.1.
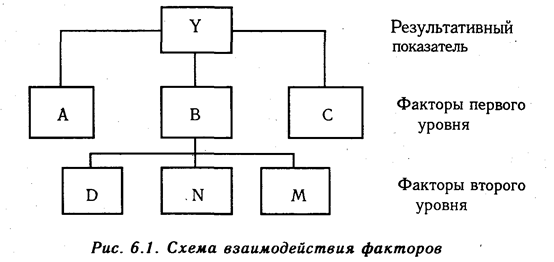
Когда известны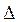 
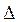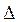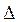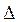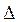Вd, Вп и Вт, а также Yb, то для определения Yd, Yn, 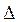Ym можно использовать способ пропорционального деления, который основан на пропорциональном распределении прироста результативного показателя Y за счет изменения фактора В между факторами второго уровня D, N и М соответственно величине их прироста. Пропорциональность этого распределения достигается путем определения постоянного для всех факторов коэффициента, который показывает величину изменения результативного показателя Y за счет изменения фактора В на единицу.
Величина коэффициента (К) определяется следующим образом:
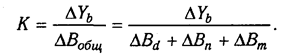
Умножив этот коэффициент на абсолютное отклонение В за счет соответствующего фактора, найдем изменение результативного показателя:
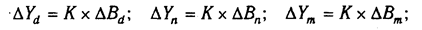
Для решения такого типа задач можно использовать также способ долевого участия. Для этого сначала определяется доля каждого фактора в общей сумме их приростов, которая затем умножается на общий прирост результативного показателя:
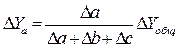
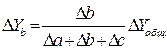
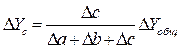
Дата: 2019-03-05, просмотров: 366.
