Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Лекция 1. Общая характеристика и взаимосвязь аналитических методов и приемов

1 Понятие методов экономического анализа

2 Связь факторов в экономическом анализе

3 Формы организации данных при проведении аналитических исследований

4 Классификация методов и приемов экономического анализа

Формы организации данных при проведении аналитических исследований

Компьютерная обработка данных

В настоящее время  анализ финансово-хозяйственной деятельности современного предприятия проводится  использования компьютерной техники . Существует множество бухгалтерских компьютерных программ, позволяющих довольно эффективно вести бухгалтерский учет и формировать отчетность. На небольших предприятиях внедряются обычно простые бухгалтерские системы типа "1-С Бухгалтерия", "Галактика", "Парус" и т.п. Эти системы имеют в своем составе минимальные аналитические возможности - обычно только расчет некоторых финансовых коэффициентов и соотношений.

Системы посложнее, например Platinum, включают в свои аналитические пакеты обработку большего объема информации, не только бухгалтерской, но и относящейся к сфере управленческого учета.

Наиболее развернутые информационные системы, такие, как BAAN или R-3, внедряются крупными производственными компаниями и позволяют не только обобщать и систематизировать бухгалтерские данные, но и в реальном времени контролировать производственные процессы. Помимо финансовой информации такие системы обрабатывают и данные в натуральном измерении.

Во всех компьютерных информационных системах, однако, функции анализа не являются основными. Целью их установки на всех предприятиях является оптимизация бухгалтерского учета и контроля за финансовыми потоками, реже - интересы эффективного планирования. Предполагается, что работать с этими системами будут сотрудники, в чьи обязанности развернутый анализ деятельности всего предприятия не входит. Поэтому сложных математических, статистических и эконометрических процедур и методов в самих бухгалтерских и управленческих информационных системах не предусмотрено. Для этого существуют специальные прикладные пакеты анализа. Хорошим примером такой аналитической системы является пакет Statistica. Небольшой, но весьма функциональный аналитический пакет входит в состав табличного процессора MSExcel, работающего в среде Windows. Компьютеры, работающие с Windows, являются наиболее распространенными в нашей стране и в мире. Поэтому, если вы уже пользуетесь таблицами Excel, есть смысл познакомиться и с его возможностями анализа данных. Пакет этот можно найти в строке меню "Данные > Анализ данных", затем выбрать из предлагаемых видов анализа интересующий вас. Очень удобен Excel для проведения корреляционного и регрессионного анализа.

За последние годы компьютеры стали обычным инструментом на большинстве предприятий, однако многие его возможности еще недооцениваются руководителями и сотрудниками планово-аналитических служб. В случаях, когда требуется обработка большого количества информации, когда необходимо разрабатывать планы, модели, пути наиболее эффективного использования ресурсов и вырабатывать оптимальные решения, компьютер является идеальным инструментом.

 

Лекция 2. Классические методы экономического анализа

1 Балансовый метод

2 Метод сравнения

3 Факторный анализ на основе детерминированных моделей

4 Прогнозирование на основе пропорциональных зависимостей

 

Балансовый метод

          Балансовый метод служит для отражения соотношений, пропорций двух групп показателей, взаимосвязанных и уравновешенных, итоги которых должны быть тождественны. Этот метод широко применяется в практике бухгалтерского учета и планирования, а также экономического анализа. В экономическом анализе балансовый метод может применяться как в качестве основного, так и вспомогательного метода. В качестве основного этот метод применяется при изучении показателей, находящихся в балансовой зависимости, например, при анализе обеспеченности предприятия сырьем, материалами, товарами, трудовыми ресурсами, кормами, при анализе бухгалтерского баланса и др. Как вспомогательный балансовый метод используется при проверке результатов расчета влияния факторов на совокупный результативный показатель. Так, в детерминированном факторном анализе алгебраическая сумма влияния отдельных факторов должна быть равна величине общего прироста результативного показателя. Если такое равенство отсутствует, то это свидетельствует о неполном учете факторов или допущенных ошибках при расчете.

Балансовый метод в экономическом анализе можно использовать при построении аддитивных факторных моделей. Например, при оценке влияния факторов на объем реализации продукции в случае если выручка на предприятии определяется по отгрузке товарной продукции используют формулу товарного баланса:

            ГПн + ТП = РП + ГПк

 Отсюда факторная модель реализованной продукции будет следующая:

РП = ГПн + ТП – ГПк

Где ГПн и ГПк – отстатки готовой продукции ан складе на начало и конец года;

ТП – стоимость товарной продукции;

РП – стоимость реализованной продукции.

 

Метод сравнения

Сравнение – это научный метод познания, в процессе которого неизвестное (изучаемое) явление сопоставляется с уже известным, изучаемым ранее с целью определения общих черт или различий между ними. С помощью приема сравнения выявляется общее и специфическое в изучаемых явлениях, рассматриваются изменения изучаемых объектов, тенденции и закономерности их развития, причинно-следственные связи между ними.

Способ сравнения предусматривает выполнение следующих этапов:

-выбор сравниваемых объектов анализа;

- выбор вида сравнения;

- выбор базы сравнения;

- выбор набора показателей, по которым будут сравниваться объекты анализа;

- выбор шкалы сравнения.

Важным условием применения приема сравнения является полная сопоставимость сравниваемых показателей. При этом должно быть учтено выполнение следующих требований:

   1 единство промежутков времени, за которые были рассчитаны сравниваемые показатели;

2 сопоставимость исходных условий производства (природных, климатических, технических и др.);

3 единство методики расчета показателей и их состав;

   4 сравниваемые явления должны быть измерены в одинаковых единицах измерения;

5 единство объемных, ценовых, качественных и структурных факторов.

Если объекты анализа не удовлетворяют некоторым из этих требований, то их надо привести в сопоставимый вид с помощью таких способов как пересчеты несравнимых показателей по единому алгоритму, приведение к одинаковым единицам измерения и др.

При проведении аналитических исследований используют горизонтальный, вертикальный, трендовый, динамический, статический, одномерный и многомерный сравнительный анализ. Горизонтальный сравнительный анализ применяют при сравнении фактического уровня показателей с данными прошлого и базисного года, планом, средним уровнем показателя и т.д.

 Вертикальный сравнительный анализ применяют при изучении структуры показателей.

Трендовый сравнительный анализ применяют при выявлении основной тенденции показателей путем сравнения фактического уровня показателей с данными предыдущих лет за более длительный период.

Динамический сравнительный анализ применяют при исследовании показателей во времени, а статический – при оценке уровня показателей одного периода по различным хозяйствующим субъектам.

Одномерный сравнительный анализ применяют при изучении показателей одного объекта или при сопоставлении нескольких объектов по одному показателю.

Многомерный сравнительный анализ применяют при изучении результатов деятельности нескольких предприятий по щирокому кругу показателей.

Проводить сравнение можно по одному или нескольким критериям. В первом случае используются следующие методы и виды сравнения:

-сравнение факта с планом (на этом методе основан анализ отклонений);

-сравнение по данному критерию в динамике, расчет среднего темпа роста (снижения) значения данного показателя за единицу времени;

-сравнение с эталоном, в качестве которого может фигурировать норматив, предприятие-конкурент и т.п.;

-ранжирование с использованием относительных показателей (например, ранжирование по рентабельности);

-использование специальных статистических показателей вместе с их характеристическими значениями (пример использования одного из таких показателей - коэффициента вариации как характеристики однородности совокупности данных).

Для проведения комплексной оценки хозяйственной деятельности предприятия сравнения по одному критерию  недостаточно. В развернутом анализе экономические субъекты сравниваются сразу по нескольким критериям (например, по уровню рентабельности, оборачиваемости, росту продаж и т.д.). При этом не все показатели равнозначны - многие из них несоизмеримы или могут действовать разнонаправленно. В этом случае следует использовать какой-либо способ ранжирования. Наиболее часто применяются метод суммы мест и таксонометрический метод. Составленные с использованием этих методов рейтинги дают комплексную оценку деятельности экономических субъектов, позволяя выявить лучшие по целому ряду показателей.

Метод суммы мест . По любому показателю совокупность анализируемых значений упорядочивается от лучшего к худшему таким образом, что лучшему значению присваивается первое место, следующему - второе и т.д. Полученные места суммируются, причем, чем меньше оказался результат, тем лучше.

Таксонометрический метод . В основу метода положены операции с матрицами. Пусть ранжирование т предприятий проводится по «n» показателям. Тогда совокупность всех значений показателей по этой группе предприятий можно представить в виде матрицы:

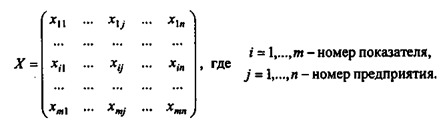
Все показатели имеют разную природу и несравнимые друг с другом значения, поэтому следующим шагом должно быть нормирование показателей. Для этого произведем замену матрицы X на матрицу Z:

Проведение процедуры нормирования снимает влияние абсолютных величин и вариации значений самих показателей.

На следующем этапе производится формирование "эталонного предприятия". Для этого в любой строке выбирается наибольшее (или наименьшее) значение соответствующего показателя в зависимости от того, какова его оптимальная величина. Характеристика эталонного предприятия – это матрица-столбец: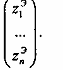

Расчет квазирасстояний R_ij от любого предприятия до эталона дает следующие значения для всех «m» предприятий:

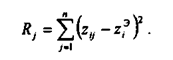
Выбор лучшего предприятия осуществляется методом наименьших квадратов. Предприятие, имеющее минимальное значение R_j, следует признать лучшим.Иногда, применяя таксонометрический метод, вводят весовые коэффициенты сравнительной значимости показателей α_j, и тогда

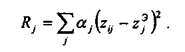
Виды средних величин

Наименование средней	Формула средней
	Простая	Взвешенная
Арифметическая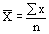
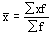
Гармоническая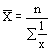
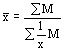
Геометрическая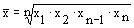
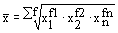
Квадратическая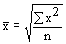

 

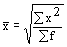
х – индивидуальное значение признака,

n – число значений признака.

 

К степенным средним относятся: средняя арифметическая, средняя гармоническая, средняя геометрическая и средняя квадратическая. Средняя обозначается через 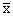. Черта вверху символизирует процесс осреднения индивидуальных значений. Частота – повторяемость отдельных значений признака – обозначается буквой f.

Вопрос о выборе средней решается в каждом отдельном случае, исходя из задач исследования и наличия исходной информации.

Средняя арифметическая простая используется в тех случаях, когда варианты или варьирующие признаки встречаются только по одному разу и имеют одинаковый вес в совокупности. Средняя арифметическая взвешенная используется, когда данные сгруппированы, а отдельные значения признака встречаются неодинаковое число раз.

Средняя гармоническая – это величина, обратная средней арифметической из обратных значений признака. Средняя гармоническая вычисляется в тех случаях, когда в качестве весов применяются не единицы совокупности, а произведения этих единиц на значения признака (то есть М=хf).

Средняя гармоническая простая исчисляется в тех случаях, когда веса одинаковы, то есть равны между собой.

Средняя геометрическая простая используется при вычислении среднего коэффициента роста (темпа роста) в рядах динамики.

Средняя квадратическая используется для расчетов среднего квадратического отклонения () при изучении темы «Показатели вариации».

Индексный метод

Индекс - это статистический показатель, представляющий собой отношение двух состояний какого-либо признака. С помощью индексов проводятся сравнения с планом, в динамике, в пространстве. Индекс называется простым ( частным, индивидуальным), если исследуемый признак берется без учета связи его с другими признаками изучаемых явлений. Простой индекс имеет вид:

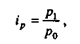
где p₁ и p₀ - сравниваемые состояния признака.

Индекс называется аналитическим (общим, агрегатным), если исследуемый признак берется не изолированно, а в связи с другими признаками. Аналитический индекс всегда состоит из двух компонент: индексируемый признак р (тот, динамика которого исследуется) и весовой признак q. С помощью признаков-весов измеряется динамика сложного экономического явления, отдельные элементы которого несоизмеримы. Простые и аналитические индексы дополняют друг друга.

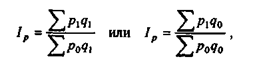
где q₀ или q₁ - весовой признак.

С помощью индексов в анализе финансово-хозяйственной деятельности решаются следующие основные задачи:

-оценка изменения уровня явления (или относительного изменения показателя);

-выявление роли отдельных факторов в изменении результативного признака;

-оценка влияния изменения структуры совокупности на динамику.

Основной  проблемой при построении аналитических индексов является проблема взвешивания. Решая ее, аналитику необходимо сначала выбрать сам весовой признак, а затем - период, на уровне которого берется признак-вес.Первая из этих задач решается довольно легко путем отыскания системы связанных признаков, произведение которых дает экономически понятный показатель. Что касается второй задачи, то научного обоснования выбора периода весов не существует, в каждом конкретном случае аналитик делает это исходя из задач анализа. Индексы, взвешенные на базовые (q₀) или отчетные (q₁) значения, имеют разный вид и по-разному могут интерпретироваться.

Признак, непосредственно относящийся к изучаемому явлению и характеризующий его количественную сторону, называется первичным или количественным. Первичные признаки объемные, их можно суммировать. Примерами таких признаков являются численность работающих на предприятии (Ч), величина основных средств (ОС) и т.д.

Признаки, относящиеся к изучаемому явлению не непосредственно, а через один или несколько других признаков и характеризующие качественную сторону изучаемого явления, называются вторичными или качественными. Отличительными особенностями вторичных признаков является то, что это всегда относительные показатели, их нельзя непосредственно суммировать в пространстве (исключение — суммирование при расчете некоторых статистик, например, коэффициентов регрессии, корреляции и др., когда экономическая природа показателя не принимается во внимание). В качестве примера можно привести показатели средней заработной платы, годовой производительности труда и т.п.

В анализе выделяют вторичные признаки первого, второго и более высоких порядков. Вторичный признак п-го порядка получается дальнейшей детализацией вторичного признака (n-l)-гo порядка. Связь признаков разных порядков можно проиллюстрировать на примере:

Существует следующее правило определения периода для признака-веса: при построении аналитических индексов по вторичным признакам рекомендуется брать веса на уровне отчетного периода, а по первичным - базисного, т.е.

Это обусловлено приоритетностью качественных показателей перед количественными: практический интерес представляет определение экономического эффекта от изменения качественного показателя, полученного в отчетном, а не в базисном периоде. Именно этот подход закладывается при реализации метода цепных подстановок в двухфакторных мультипликативных моделях (в многофакторных моделях привлекается еще и понятие вторичности n-го порядка).

 

Большое значение имеет применение индексного метода при проведении факторного анализа, так как позволяет определить не только абсолютные отклонения результативного показателя за счет факторов, но и относительные. Например, индекс изменения выпуска продукции (Увп) можно выразить через произведение индексов численности работников (Ур) и их среднегодовой производительности труда (Угп):

                    Увп = Ур х Угп

При этом расчет индексов производится по следующим формулам:

        Ур =  Ро х ГПб

                  Рб х ГПб

        Угп = Ро х ГПо

                    Ро х ГПб

         У вп =    Ро х ГПо

                           РохГПб
      Рассчитанные индексы численности рабочих и производительности труда показывают относительное (в %) изменение валовой продукции за счет влияния этих факторов, индекс валовой продукции отражает ее общее процентное изменение. Чтобы определить абсолютное изменение валовой продукции за счет влияния каждого фактора необходимо из числителя индекса соответствующего фактора вычесть его знаменатель:

      ∆ ВПр = Ро х ГПб – Рб х ГПб

      ∆ ВПгп = Ро х ГПо – Ро х ГПб

       ∆ВПобщее = Ро х ГПо – Рб х ГПб

 

Регрессионный анализ

С корреляционным анализом тесно связан регрессионный анализ - это метод установления аналитического выражения стохастической зависимости между исследуемыми признаками.

Уравнение регрессии показывает, как в среднем изменяется у при изменении любого из x_i, и имеет вид:

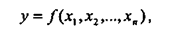
где у - зависимая переменная (она всегда одна);

х_i - независимые переменные (факторы) (их может быть несколько).

Если независимая переменная одна - это простой регрессионный анализ. Если же их несколько (п 2), то такой анализ называется многофакторным.

В ходе регрессионного анализа решаются две основные задачи:

-построение уравнения регрессии, т.е. нахождение вида зависимости между результатным показателем и независимыми факторами x₁, x₂, …, x_n.

- оценка значимости полученного уравнения, т.е. определение того, насколько выбранные факторные признаки объясняют вариацию признака у.

Применяется регрессионный анализ главным образом для планирования, а также для разработки нормативной базы.

В отличие от корреляционного анализа, который только отвечает на вопрос, существует ли связь между анализируемыми признаками, регрессионный анализ дает и ее формализованное выражение. Кроме того, если корреляционный анализ изучает любую взаимосвязь факторов, то регрессионный - одностороннюю зависимость, т.е. связь, показывающую, каким образом изменение факторных признаков влияет на признак результативный.

Регрессионный анализ - один из наиболее разработанных методов математической статистики. Для реализации регрессионного анализа необходимо выполнение ряда специальных требований (в частности, x_l,x₂,...,x_n; y должны быть независимыми, нормально распределенными случайными величинами с постоянными дисперсиями). В реальной жизни строгое соответствие требованиям регрессионного и корреляционного анализа встречается очень редко, однако оба эти метода весьма распространены в экономических исследованиях. Зависимости в экономике могут быть не только прямыми, но и обратными и нелинейными. Регрессионная модель может быть построена при наличии любой зависимости, однако в многофакторном анализе используют только линейные модели вида:

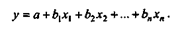
Построение уравнения регрессии осуществляется, как правило, методом наименьших квадратов, суть которого состоит в минимизации суммы квадратов отклонений фактических значений результатного признака от его расчетных значений, т.е.:

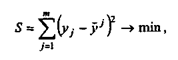
где т - число наблюдений;

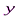^j = a + b₁x₁^j + b₂x₂^j+ ... + b_nх_n^j - расчетное значение результатного фактора.

Коэффициенты регрессии рекомендуется определять с помощью аналитических пакетов для персонального компьютера или специального финансового калькулятора. В наиболее простом случае коэффициенты регрессии однофакторного линейного уравнения регрессии вида y = а + bх можно найти по формулам:

 

 

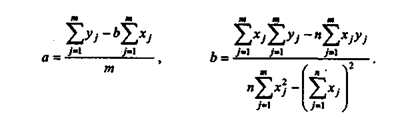
   3  Использование методики парной корреляции

Алгоритм расчетов при корреляционном анализе связи парной корреляции состоит из следующих этапов:

1 Проводится отбор наиболее важных факторов, влияющих на результативный показатель, с учетом причинно-следственных связей между показателями. При этом все факторы должны быть количественно измеримы. Отбор показателей для анализа и придание им статуса фактора или результативного показателя проводится на основе знания экономических законов.

2 Выбранные факторы наносятся на поле координат, то есть строится корреляционное поле.

3 Проводится обоснование формы связи: по форме корреляционного поля; путем визуального анализа ранжированного (в порядке возрастания или убывания) ряда факторов. Форма связи между показателями определяет дальнейшие действия корреляционного анализа. Например, если связь носит прямолинейный характер, то рассчитывается коэффициент корреляции, который дает количественную оценку тесноты связи.

4 Выбирается и решается уравнение регрессии.

   Наиболее простым уравнением, характеризующим прямолинейную зависимость между двумя показателями, являются уравнение прямой:

                                       Ух = а+bх

где, х - факторный показатель;

  У - результативный показатель;

  а, b - параметры уравнения регрессии, которые надо отыскать. Причем b - коэффициент регрессии несет основную смысловую нагрузку. Он показывает насколько единиц в среднем изменится результативный показатель (У) с изменением на одну единицу факторного признака (х). Эта величина на графике показывает угол наклона прямой. Свободный член а показывает начальную ординату, то есть расстояние от начала координат до пересечения прямой с осью У.

       Значения коэффициентов а и b находят способом наименьших квадратов. Он основан на предположении, что линия, выравнивающая эмпирические данные, должна проходить так, чтобы сумма квадратов отклонений от этой линии была наименьшей. Используя способов наименьших квадратов, первоначальное уравнение прямой примет следующий вид:

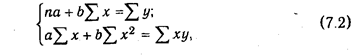
где п - количество наблюдений.

Однако, уравнения регрессии еще не дает ответа на вопрос: какова теснота связи между показателями, решающее или нет влияние оказывает фактор на результативный показатель. Для измерения тесноты связи между факторами и результативным показателем рассчитывается коэффициент корреляции. В случае прямолинейно связи коэффициент корреляции рассчитывается по формуле:

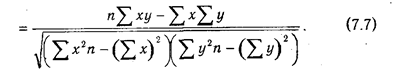
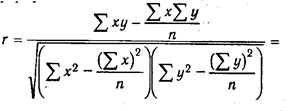
   Коэффициент корреляции может принимать значения от 0 до 1.

При r = 0, связь между показателями отсутствует;

если r = 1, связь функциональная (детерминированная);

если r<0, то связь между показателями обратная;

если r>0, то связь между показателями прямая.

      Чем ближе коэффициент корреляции к 1, тем более тесная связь между показателями. Теснота связи между показателями при различных значениях корреляционного соотношения представлена в таблице 2.

Таблица 2 Качественная оценка тесноты связи при различных значениях корреляционного соотношения.

Величина коэффициента корреляции	01-0,3	0,3-0,5	0,5-0,7	0,7-0,9	-0,9-0,99
Теснота связи	слабая	умеренная	заметная	высокая	очень высокая

 

        Если коэффициент корреляции возвести в квадрат: (0,66² = 0,435), то получим коэффициент детерминации (d), который показывает, на сколько процентов результативный показатель зависит от изучаемого фактора. (урожайность зерновых культур на 43,5 % зависит от качества почвы, а на 56,5 % от влияния других факторов.)

         

Эвристические методы

 Эвристические методы относятся к неформальным методам решения экономических задач. Они используются в основном для прогнозирования состояния объекта в условиях частичной или полной неопределенности, когда основным источником получения необходимых сведений служит интеллектуальный потенциал профессионалов, работающих в определенных сферах науки и бизнеса. Наиболее распространенным из них является метод экспертных оценок — организованный сбор суждений и предложений специалистов (экспертов) по исследуемой проблеме с последующей обработкой полученных ответов. Основой данного метода является опрос специалистов, который может быть индивидуальным, коллективным, очным, заочным, анонимным и так далее. Организаторы опроса определяют объект и цели экспертизы, подбирают экспертов, проверяют их компетентность, анализируют и обобщают результаты экспертизы.

Можно выделить следующие основные разновидности метода экспертных оценок:

а) метод «мозговой атаки» или конференции идей — поиск новых идей, их широкое обсуждение и конструктивная критика, где генерирование идей происходит в процессе творческого спора и личного контакта специалистов. При этом необходимо четко сформулировать проблему, выделив в ней центральное звено; поддерживать идею любого рода, даже если она кажется сомнительной; не прекращать обсуждение и поощрять любую идею, чтобы участники не чувствовали скованности;

б) метод «мозгового штурма»: одна группа экспертов выдвигает идеи, а другая их анализирует;

в) синектический метод предполагает использование при генерировании идей аналогий из других областей знаний или фантастики;

г) метод Дельфи — анонимный опрос специалистов по заранее подготовленным вопросам с последующей статистической обработкой информации. После обобщения результатов повторно запрашивается мнение специалистов по спорным вопросам. В итоге обеспечивается переход от интуитивных форм мышления к дискуссионным формам. Для этого метода характерны, изолированность в работе и независимость суждений каждого члена экспертной группы;

д) метод «дерева целей» — использование иерархической структуры решения проблемы путем разделения общей цели на I подцели. Вершина дерева целей представляет собой цели, а «ветви» — это связи между ними. Экспертам предлагается оценить структуру модели системы в целом и дать предложения по ее совершенствованию. Результаты анонимного анкетирования обобщаются и доводятся до экспертов, что позволяет им корректировать свои суждения на основе полученной информации;

е) метод ПАТТЕРН — помощь планированию посредством количественной оценки технических данных. Изучаемая проблема расчленяется на ряд подпроблем, задач и элементов, которые выстраиваются в «дерево решений». Оценки отдельных экспертов подвергаются открытому обсуждению, в результате чего извлекается польза от делового общения экспертов, хотя не исключаются отрицательные последствия конформизма (давление авторитетов);

ж) метод сценариев — экспертная оценка возможных вариантов развития событий и выбор наиболее реальных и благоприятных. Один из эффективных средств прогнозирования. Сценарий — это модель будущего состояния предприятия, которая описывает возможный ход событий, рассматривает факторы, которые могут оказать влияние на ход предполагаемых событий. Обычно в качестве базового сценария рассматривается наиболее вероятный вариант, который служит базой для принятия решения. Другие варианты (оптимистический, пессимистический) считаются альтернативными.

Наиболее простым методом прогнозирования является применение среднего абсолютного прироста и среднего темпа роста динамического ряда.

Методы экстраполяции

Экстраполяция представляет собой метод прогнозирования, заключающийся в изучении сложившихся в прошлом и настоящем устойчивых тенденций развития процессов и явлений и переносе их на будущее. Метод экстраполяции применим при следующих допущениях:

а) период времени, для которого построена функция, должен быть достаточным для выявлении тенденции развития;

 б) анализируемый процесс является устойчиво динамическим и обладает инерционностью, т.е. для значительных изменений характеристик процесса требуется время;

в) не ожидается сильных внешних воздействий на изучаемый процесс, которые могут серьезно повлиять на тенденцию развития.

Прогнозирование с помощью метода экстраполяции – один из простейших методов статистического прогнозирования. Его использование оправдано при недостаточном знании о природе изучаемого явления или отсутствии данных, необходимых для применения более совершенных методов прогнозирования.

Различают простую экстраполяцию, которая предполагает, что все действовавшие в прошлом и настоящем тенденции сохранятся в полном объеме, так как все действовавшие факторы останутся неизменными;  прогнозную экстраполяцию, которая базируется на предположении об изменении факторов, определяющих динамику изучаемого процесса или явления.

При формировании прогнозов с помощью экстраполяции обычно исходят из статистически складывающихся тенденций изменения тех или иных количественных характеристик объекта. Экстраполируются оценочные функциональные системные и структурные характеристики. Экстраполяционные методы являются одними из самых распространенных и наиболее разработанных среди всей совокупности методов прогно­зирования. С помощью этих методов экстраполируются количественные параметры больших систем, количественные характеристики экономического, научного, производственного потенциала, данные о результа­тивности научно-технического прогресса, характеристики соотношения отдельных подсистем, блоков, элементов в системе показателей сложных систем и др. Однако степень реальности такого рода прогнозов и соответ­ственно мера доверия к ним в значительной мере обусловливаются аргументированностью выбора пределов экстраполяции и стабиль­ностью соответствия "измерителей" по отношению к сущности рас­сматриваемого явления. При этом  слож­ные объекты, как правило, не могут быть охарактеризованы одним параметром. В связи с этим можно сделать некоторое представление о последовательности действий при статистическом анализе тенден­ций и экстраполировании, которое состоит в следующем:

- во-первых, должно быть четкое определение задачи, выдвиже­ние гипотез о возможном развитии прогнозируемого объекта, обсуж­дение факторов, стимулирующих и препятствующих развитию данного объекта, определение необходимой экстраполяции и её допустимой дальности;

- во-вторых, выбор системы параметров, унификация различных единиц измерения, относящихся к каждому параметру в отдельности;

- в-третьих, сбор и систематизация данных. Перед сведением их в соответствующие таблицы еще раз проверяется однородность дан­ных и их сопоставимость: одни данные относятся к серийным изде­лиям, а другие могут характеризовать лишь конструируемые объекты;

- в-четвертых, когда вышеперечисленные требования выполнены, задача состоит в том, чтобы в ходе статистического анализа и не­посредственной экстраполяции данных выявить тенденции или симп­томы изменения изучаемых величин. В экстраполяционных прогнозах особо важным является не столько предсказание конкретных значе­ний изучаемого объекта или параметра в таком-то году, сколько своевременное фиксирование объективно намечающихся сдвигов, ле­жащих в зародыше назревающих тенденций.

Для повышения точности экстраполяции используются различные приемы. Один из них состоит, например, в том, чтобы экстраполи­руемую часть общей кривой развития (тренда) корректировать с уче­том реального опыта развития отрасли-аналога исследований или объекта, опережающих в своем развитии прогнозируемый объект. При этом под трендом понимается характеристика основной закономер­ности движения во времени, в некоторой мере свободной от случай­ных воздействий. Тренд - это длительная тенденция изменения эко­номических показателей. При разработке моделей прогнозирования тренд оказывается основной составляющей прогнозируемого времен­ного ряда, на которую уже накладываются другие составляющие. Ре­зультат при этом связывается исключительно с ходом времени. Пред­полагается, что через время можно выразить влияние всех основ­ных факторов.

Под тенденцией развития понима­ют некоторое его общее направление, долговременную эволюцию. Обычно тенденцию стремятся представить в виде более или менее гладкой траектории.

Анализ показывает, что ни один из существующих методов не может дать достаточной точности прогнозов на 20-25 лет. Применяе­мый в прогнозировании метод экстраполяции не дает точных резуль­татов на длительный срок прогноза, потому что данный метод исхо­дит из прошлого и настоящего, и тем самым погрешность накапли­вается. Этот метод дает положительные результаты на ближайшую перспективу прогнозирования тех или иных объектов не более 5 лет.

Для нахождения параметров приближенных зависимостей между двумя или несколькими прогнозируемыми величинами по их эмпиричес­ким значениям применяется метод наименьших квадратов. Его сущ­ность состоит в минимизации суммы квадратов отклонений меж­ду наблюдаемыми (фактическими) величинами и соответствующими оценками (расчет­ными величинами), вычисленными по подобранному уравнению связи. Этот метод лучше других соответствует идее усреднения как единичного влияния учтенных факторов, так и общего влияния неуч­тенных.

Рассмотрим простейшие приемы экстраполяции. Операцию экстра­поляции в общем виде можно представить в виде определения значе­ния функции:

,

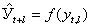где 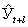- экстраполируемое значение уровня;

    L – период упреждения;

   У_t – уровень, принятый за базу экстраполяции.

Под периодом упреждения при прогнозировании понимается от­резок времени от момента, для которого имеются последние статис­тические данные об изучаемом объекте, до момента, к которому относится прогноз.

1.Экстраполяция на основе среднего значения временного ряда. В самом простом случае при предположении о том, что средний уровень ряда не имеет тенденции к изменению или если это изменение незначительно, можно принять 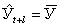т.е. прогнозируемый уровень равен среднему значению уровней в прошлом. Доверительные границы для средней при небольшом числе на­блюдений определяются следующим образом:

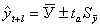
где t_a – табличное значение t – статистики Стьюдента с n-1 степенями и уровнем вероятности p;

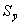- средняя квадратическая ошибка средней величины. Значение ее определяется по формуле .

В свою очередь, среднее квадратическое отклонение для выборки равно:

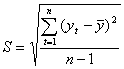
где y_t – фактические значения показателя.

Доверительный интервал, полученный как t_{a 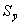,} учитывает неопределенность, которая связана с оценкой средней величины. Общая дисперсия, связанная как с колеблемостью выборочной средней, так и с варьированием ндивидуальных значений вокруг средней, составит величину S²+S²/n. Таким образом, доверительные интервалы для прогностической оценки равны:

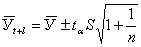
2. Экстраполяция по скользящей и экспоненциальной средней. Для краткосрочного прогнозирования наряду с другими приемами могут быть применены адаптивная или экспоненциальная скользящие сред­ние. Если прогнозирование ведется на один шаг вперед, то 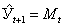или ,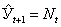

 где М_t - адаптивная скользящая средняя;

   N_t - экспоненциальная средняя.

Здесь доверительный интервал для скользящей средней можно определить по выше приведенной формуле , в которой число наблюдений обозначено символом n. Поскольку при расчете скользящей средней через m обозначалось число членов ряда, участвующих в расчете средней, то заменим в этой фор­муле n на m, равным нечетным числам.

При экспоненциальном сглаживании дисперсия экспоненциальной средней равна ,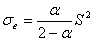

 где S -среднее квадратическое отклонение, вместо величины 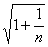в фор­муле (2.10) при исчислении доверительного интервала прогноза следует взять величину 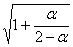или 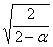. Здесь a- коэффициент экспоненциального сглаживания, изменяется от 0 до 1. Если 0<a<0,5, то при расчете прогноза учитываются прошлые значения временного ряда, а при 0,5<a<1 – значения, близкие к периоду упреждения. Примерное значение коэффициента сглаживания определяют по формуле Р.Брауна:

,

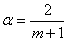где m – число уровней временного ряда, входящих в интервал сглаживания.

3. Экстраполяция на основе сред­него темпа. Если в основу прогностического расчета положен средний темп роста, то экстраполируемое значение уровня можно получить с помощью формулы: 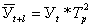, 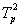где - средний темп роста, У_t - уровень, принятый за базу для экстра­поляции. Здесь принят только один путь развития - развитие по геометрической прогрессии, или по экспонентной кривой. Во мно­гих же случаях фактическое развитие явления следует иному зако­ну, и экстраполяция по среднему темпу нарушает основное допуще­ние, принимаемое при экстраполяции, - допущение о том, что раз­витие будет следовать основной тенденции - тренду, наблюдавшему­ся в прошлом. Чем больше фактический тренд отличается от экспоненты, тем больше данные, получаемые при экстраполяции тренда, будут отличаться от экстраполяции на основе среднего темпа.

Средний темп или определяется на основе изучения прошлого, или оценивается каким-либо другим путем (например, подбор вари­антов для различных ситуаций). В качестве исходного (базового) уровня для экстраполяции представляется естественным взять по­следний уровень ряда, поскольку будущее развитие начинается имен­но с этого уровня.

Статистическая надежность вышеприведенных методов оценивается с помощью коэффициента вариации:

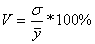
где 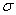- среднее квадратическое отклонение;

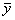- среднее значение временного ряда.

Метод считается статистически надежным и может быть использован для прогнозирования, если значение коэффициента вариации не превышает 10%.

 

Лекция 1. Общая характеристика и взаимосвязь аналитических методов и приемов

1 Понятие методов экономического анализа

2 Связь факторов в экономическом анализе

3 Формы организации данных при проведении аналитических исследований

4 Классификация методов и приемов экономического анализа