Четырехклеточные таблицы – это частотные таблицы, построенные для двух дихотомических признаков. Встает вопрос – надо ли изучать эти таблицы отдельно? Ведь они представляют собой частный случай всех возможных таблиц сопряженности. Выше мы обсуждали коэффициенты, которые можно использовать для анализа любой частотной таблицы, в том числе и для четырехклеточной. Однако ответ на наш вопрос положителен. Причин тому несколько.
Во-первых, многие известные коэффициенты для четырехклеточных таблиц оказываются равными друг другу. И по крайней мере надо знать об этом, чтобы не осуществлять заведомо ненужные выкладки.
Во-вторых, оказыватся, что именно в анализе четырехклеточных таблиц можно увидеть нечто полезное для социолога, но не высвечивающееся на таблицах большей размерности.
В-третьих, с помощью анализа специальным образом организованных четырехклеточных таблиц оказывается возможным перейти от изучения глобальных связей к изучению локальных и промежуточных между первыми и вторыми (о промежуточных связях мы говорили в п.2.2.1).
Итак, рассмотрим два дихотомических признака – Х и Y, принимающие значения 0 и 1 каждый, и отвечающую им четырехклеточную таблицу сопряженности (табл. 1).
Ниже будем использовать пример, когда рассматриваются два дихотомических признака – пол (1 – мужчина, 0 – женщина) и курение (1 – курит, 0 – не курит) (см. табл. 2).
Таблица 1. Общий вид четырехклеточной таблицы сопряженности
| X | Y | Итого | |
| 1 | 0 | ||
| 1 | a | b | a+b |
| 0 | c | d | c+d |
| Итого | a+c | b+d | a+b+c+d |
буквы в клетках обозначают соответствующие частоты
Таблица 2. Пример четырехклеточной таблицы сопряженности
| Курение | Пол | Итого | |
| м | ж | ||
| Курит | 80 | 4 | 84 |
| Не курит | 10 | 6 | 16 |
| Итого | 90 | 10 | 100 |
Данные таблицы 2 говорят о том, что в нашей совокупности имеется 90 мужчин, из которых 80 человек курят, и 10 женщин, среди которых 4 человека курящих и т.д.
Все известные коэффициенты связи для четырехклеточных таблиц основаны на сравнении произведений ad и bc. Если эти произведения близки друг к другу, то полагаем, что связи нет. Если они совсем не похожи – связь есть. Основано такое соображение на том, что равенство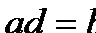 
эквивалентно равенству 
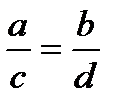, что, в свою очередь, означает пропорциональность столбцов (строк) нашей частотной таблицы, т.е отсутствие статистической связи. Чем более отличны друг от друга указанные произведения, тем менее пропорциональны столбцы (строки) и, стало быть, тем больше оснований имеется у нас полагать, что переменные связаны. Для обоснования этого утверждения могут быть использованы те же рассуждения, что были приведены выше. А именно, можно показать, что разница между наблюдаемой и теоретической частотой для левой верхней клетки нашей четырехклеточной частотной таблицы (нетрудно проверить, что наличие или отсутствие связи для такой таблицы определяется содержанием единственной клетки - при заданных маргиналах частоты, стоящие в других клетках, можно определить однозначно) равна величине [Кендалл, Стьюарт, 1973. С. 722]:
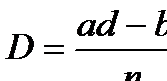
Коэффициенты, основанные на описанной логике, могут строиться по-разному. Но всегда они базируются либо на оценке разности (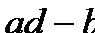 
), либо на оценке отношения 
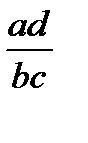. В первом случае об отсутствии связи будет говорить близость разности к нулю, во втором – близость отношения к единице. Естественно, ни разность, ни отношение не могут служить искомыми коэффициентами в “чистом” виде, поскольку их значения зависят от величин используемых частот. Требуется определенная нормировка. И, как мы уже оговаривали выше, желательно, чтобы искомые показатели связи находились либо в интервале от -1 до 1, либо – от 0 до 1, Возможны разные ее варианты. Это обуславливает наличие разных коэффициентов – показателей связи для четырехклеточных таблиц. Рассмотрим два наиболее популярных коэффициента.
Коэффициент ассоциации Юла:
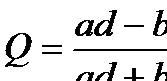
и коэффициент контингенции
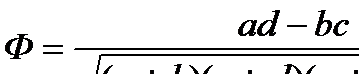
Коротко рассмотрим их основные свойства.
Оба коэффициента изменяются в интервале от -1 до +1 (значит, для них имеет смысл направленность связи; о том, что это такое в данном случае, пойдет речь ниже). Обращаются в нуль в случае отсутствия статистической зависимости, о котором мы говорили выше (независимость признаков связана с пропорциональностью столбцов таблицы сопряженности). А вот в единицу (или - 1) эти коэффициенты обращаются в разных ситуациях. Они схематично отражены ниже.
| Свойства коэффициентов: | Q = 1 | Q = -1 | Ф = 1 | F = -1 | ||||
| Отвечающие им виды таблиц | a | 0 | 0 | b | a | 0 | 0 | b |
| c | d | c | d | 0 | d | c | 0 | |
| a | b | a | b |
|
| |||
| 0 | d | c | 0 | |||||
| (а) | (б) | (в) | (г) | |||||
Рис. 1. Схематическое изображение свойств коэффициентов Q и Ф.
Таким образом, мы видим, что Q обращается в 1, если хотя бы один элемент главной диагонали частотной таблицы равен 0. Для обращения же в 1 коэффициента F необходимо обращение в 0 обоих элементов главной диагонали. Нужны ли социологу оба коэффициента? Покажем, что каждый из них позволяет выделять свои закономерности. Или, как мы говорили выше – за каждым из них стоит своя модель изучаемого явления, свое понимание связи, выделение как бы одной стороны того, что происходит в реальности. Постараемся убедить читателя, что социолога должны интересовать обе эти стороны.
Вопросы для самопроверки
1. Каковы коэффициенты связи, основанные на понятии энтропии?
2. Каковы коэффициенты связи для четырехклеточных таблиц сопряженности?
Лекция 14.
Анализ связей типа "альтернатива – альтернатива". Смысл локальной связи. Возможные подходы к ее изучению.
При обсуждении прогнозных и информационных коэффициентов связи мы говорили о том, что знание какого-то одного значения Х может нам дать очень большую информацию об Y, а для другого значения Х аналогичная информация может быть мала. Это и означает, что для первого значения Х имеет место сильная локальная связь.
Сами термины “локальный” и “глобальный” применительно к пониманию связи между переменными, вероятно, впервые были использованы в [Чесноков, 1982].В п. 2.2.1 мы уже упоминали, что “локальному” подходу в этой работе отвечает понимание связи как некоторого отношения между двумя конкретными градациями а и b признаков Х и Y соответственно. В таком случае мы можем говорить о сильной связи, если из того, что для некоторого объекта первый признак принимает значение а, с большой вероятностью следует, что второй признак для того же объекта принимает значение b. И можно говорить о слабой связи, если аналогичная вероятность мала (еще раз напомним, что “глобальная” связь - это результат определенного “усреднения” подобных локальных связей).
Для изучения локальной связи можно использовать, например, коэффициенты Ф и Q. Для этого надо исходную частотную таблицу произвольной размерности привести к определенной четырехклеточной. Покажем на примере, как это делается. Рассмотрим частотную таблицу, выражающую зависимость между
Таблица 1.
Пример таблицы сопряженности
| Профессия | Читаемая газета | Итого | |||
| УГ | МК | Независимая | Правда | ||
| Врач | 5 | 2 | 13 | 8 | 28 |
| Токарь | 6 | 24 | 7 | 13 | 50 |
| Учитель | 9 | 0 | 1 | 0 | 10 |
| Космонавт | 2 | 1 | 4 | 5 | 12 |
| Итого | 22 | 27 | 25 | 26 | 100 |
профессией человека и читаемой им газетой (для простоты предполагаем, что каждый респондент может читать не более одной газеты). Предположим, что нас интересует локальная связь между свойством “быть учителем” и свойством “читать "Учительскую газету" (УГ)”. Упомянутая выше четырехклеточная таблица будет иметь вид:
Таблица 2.
Четырехклеточная таблица сопряженности, полученная из таблицы 1
| Профессия | Читаемая газета | Маргиналы по строкам | |
| УГ | Не УГ | ||
| Учитель | 9 | 1 | 10 |
| Не учитель | 13 | 77 | 90 |
| Маргиналы по столбцам | 22 | 78 | 100 |
Представляется очевидным, что если мы далее будем использовать коэффициенты связи, предназначенные для анализа четырехклеточных таблиц, то как раз и измерим силу нашей локальной связи.
Детерминационный анализ (ДА). Выход за пределы связей рассматриваемого типа.
В [Чесноков, 1982] для обозначения того объекта, который является носителем локальной связи, вводится понятие детерминации, обозначаемой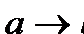 
(отметим, однако, что мы несколько вольно трактуем указанное определение, поскольку автор названной работы принципиально отвергает связь детерминации с вероятностью, говоря только об относительных частотах; о них ниже пойдет речь, и мы их будем расценивать как выборочные оценки соответствующих условных вероятностей). Детерминация определяется как носитель локальной связи или как нечто, задаваемой двумя величинами: интенсивностью (точностью, истинностью) 
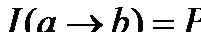и емкостью (полнотой) 
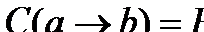(справа стоят относительные частоты).
Рассмотрим приведенную выше таблицу и детерминацию (учитель® УГ). Интенсивность и емкость в этом случае будут выглядеть следующим образом:
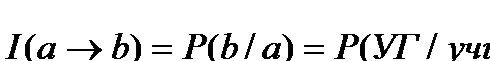
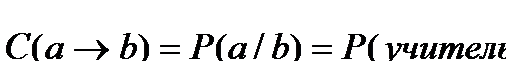
Итак, если мы хотим полностью охарактеризовать связь между свойством “быть учителем” и свойством “читать УГ”, то должны учесть два числа - долю читающих УГсреди учителей (90%) и долю учителей среди читающих УГ (41%). При всей своей простоте, это соображение далеко не всегда учитывается социологами. Частая ошибка применительно к нашему случаю означает, что исследователь узнает, что почти все учителя читают УГ и делает вывод, состоящий в том, что аудитория УГ в основном состоит из учителей. Конечно, логика здесь “хромает” - действительно, учителя составляют менее половины аудитории УГ.
Таким образом, для полного изучения "взаимодействия"двух альтернатив (т.е. изучения детерминации) необходимо принимать во внимание обе величины - и емкость, и интенсивностьдетерминации. Казалось бы, это достаточно очевидное положение.Тем не менее, социолог часто на практике про это забывает (илихочет "забыть"?!).Приведем пример того, как это обстоятельство приводит кнеправильной интерпретации исследователем имеющихся в его распоряжении данных.
После выборов в государственную Думу, прошедших в декабре1995 года, во многих средствах массовой информации обыгрывалсятот факт, что среди голосовавших за КПРФ была относительно мала доля людей с высшим образованием. Действительно, она быламеньше, чем аналогичная доля среди голосовавших, скажем заЯблоко или НДР. Естественно, из этого обстоятельства делалсявывод о том, что образованные люди не голосуют за компартию.
Но, вспоминая наши показатели, можно сказать, что, делаяэтот вывод, журналисты опирались только на сравнение величинемкостей детерминаций
(высшее образование) → (голосование за КПРФ),
(высшее образование) → (голосование за "Яблоко"),
(высшее образование) → (голосование за НДР),
т.е. на величины долей людей с высшим образованием средиголосовавших за разные партии. Однако обратимся к анализу интенсивностей тех же детерминаций. Оказывается, что за компартию в декабре проголосовало 1, 54 миллиона избирателей с высшим образованием, за "Яблоко" - 1, 43 миллиона, за НДР - 1, 3 миллиона ("Советская Россия", 21 марта 1996 года). Другимисловами, среди лиц с высшим образованием доля проголосовавшихза КПРФ (т.е. емкость первой детерминации), больше, чем доляпроголосовавших за "Яблоко" и НДР (т.е. емкости второй итретьей детерминации). Так за кого голосуют люди с высшим образованием? Предыдущий вывод вряд ли справедлив.
Вычисление интенсивности и емкости изучаемых детерминаций – основной элемент детерминационного анализа. При всей своей простоте этот подход заключает в себе глубокий смысл, поскольку требование обязательного вычисления названных показателей является своеобразной защитой от недосмотра социологов.
Кроме того, детерминационный анализ не сводится в анализу тех связей, которые мы назвали связями типа “альтернатива-альтернатива”. Он включает в себя целую систему алгоритмов, позволяющих повышать интенсивность и емкость рассматриваемых детерминаций, за счет учета значений множества признаков. Поясним подробнее, о чем здесь идет речь. Однако сначала отметим, что иногда в рамках детерминационного анализа используется терминология, несколько отличная от приведенной выше: интенсивность детерминации называется ее точностью, емкость – полнотой, сама детерминация – правилом "Если а, то b". "а" называется при этом объясняющим признаком, "b" – объясняемым. Замети, что Термин “признак” здесь используется в том смысле, который мы придавали словосочетанию “значение (альтернатива, градация) признака”. Надеемся, такое смешение терминов в данном параграфе не приведет к недоразумениям.
Предполагается, что в качестве объясняющего признака могут выступать конъюнкции и дизъюнкции любых значений рассматриваемых признаков-предикторов. При этом совокупность последних является “плавающей”. Все признаки-предикторы в таком случае называются объясняющими.
Процитируем некоторые положения из [Да-система…,1997. С. 160-161].
“Точность правила “Если а, то b” вычисляется по формуле:
,
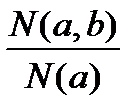где N (a,b) – количество объектов, обладающих одновременно объясняющим признаком а и объясняемым признаком b (количество подтверждений правила); N(a) – количество объектов, обладающих объясняющим признаком а безотносительно к любым другим признакам (количество применений правила). Точность измеряется от 0 до 1. Точность правила “Если а, то b” есть мера достаточности а для наличия b. Точность правила – это главный критерий его практической ценности. Наиболее ценятся правила, имеющие точность, близкую к 1.
Полнота правила – это мера его единственности. Она вычисляется по формуле:
,
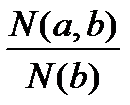Где N (b) – количество объектов, обладающих объясняемым признаком b безотносительно к любым другим признакам (объем объясняемого признака). Полнота изменяется от 0 до 1. Полнота правила “Если а, то b” есть мера необходимости а для наличия b. Полнота правила – это второй по значимости (после точности) критерий его практической ценности. Предельно точные правила ценятся тем выше, чем больше их полнота. Однако наличие высокой полноты не обязательно. Система точных правил, каждое из которых имеет небольшую полноту, может иметь чрезвычайную полезность для практики и науки, если ее суммарная полнота близка к 1”.
Пакет, реализующий детерминационный анализ [Да-система…,1997], позволяет эффективно подбирать конъюнкции объясняющих признаков для повышения точности правила, дизъюнкции – для повышения его полноты.
Например, предположим, что объясняемое положение – голосование за кандидата N. Допустим, что 40% мужчин проголосовали за N. Это значит, что точность правила “если мужчина, то голосует за N“ равна 0,4. Если мы рассмотрим мужчин с высшим образованием, точность детерминации может повыситься (а может, конечно, и не повыситься, и даже понизиться). Так, например, может оказаться, что за N проголосовали 80% мужчин с высшим образованием. Это будет означать, что, взяв конъюнкцию значения признака “пол”, означающее мужчину, и значения признака “образование”, отвечающее высшему образованию, мы повысили точность детерминации по сравнению с тем случаем, когда не учитывали образование респондента. Аналогичные рассуждения справедливы для полноты детерминации : ее тоже можно повышать с помощью удачного подбора объясняющих признаков.
Для сравнения ДА с другими алгоритмами, решающими сходные задачи, необходимо упомянуть еще два определения из [Да-система…,1997. С.161-162].
“Если какой-либо объясняющий признак убрать из правила, точность правила, вообще говоря, изменится. Величина этого изменения (с учетом знака) и есть, по определению, вклад объясняющего признака в точность. Рассмотрим правило “если а и b, то с". Вклад S (a) объясняющего признака в точность вычисляется по формуле
S(a) = (Точность правила "если а и b, то с“) – (точность правила “если b, то с").
Аналогично вычисляется вклад любого объясняющего признака в точность в любом заданном правиле." Совершенно аналогично определяется Вклад Q (a) объясняющего признака в полноту.
Заметим, что пакет программ, реализующий идеи детерминационного анализа на РС (ДА-система), пользуется большоя популярностью у социологов.
Более подробно мы не будем рассматривать ДА. Автор подхода, разработчики соответствующих программ для ЭВМ активно занимаются его пропагандой среди социологов. Однако в определенной мере мы вернемся к обсужденным положениям в п.п. 2.5.4 и 2.5.5, где попытаемся проанализировать ДА с точки зрения возможностей выявления обобщенных взаимодействий и сравнить его с методами поиска логических закономерностей.
Отметим только один факт, очень важный для нас в методологическом аспекте: автор детерминационного анализа развил его дальше, оригинальным образом обобщив положения аристотелевской силлогистики и построив стройную математическую теорию, отвечающую естественной логике социолога, “невооруженным глазом” анализирующего частотные таблицы [Чесноков, 1985]. Рождение этой теории является ярким примером того, как социологические потребности могут служить толчком для развития новых ветвей математики.
Анализ связей типа "группа альтернатив–группа альтернатив" и примыкающие к нему задачи
Итак, мы проанализировали суть связей типа "альтернатива× альтернатива", убедились в важности их изучения. Нетрудновидеть, что логика, сходная с использованной выше, приводит кмысли о необходимости изучения подобных связей для таких ситуаций, когда вместо отдельных альтернатив фигурируют их группы. Например, вместо задачи изучения связи между свойствами"быть учителем" и "читать Учительскую газету" мы можем поставить задачу проанализировать зависимость между свойствами"быть учителем, или врачом, или научным сотрудником, илииметь одну из т. н. творческих профессий" и "читать Литературную газету или журнал Новый Мир". Казалось бы, никаких проблемпри решении такой задачи не должно возникать. Нужно толькорассмотреть отвечающую нашим альтернативам подтаблицу исходной"большой" таблицы сопряженности и применить к ней уже знакомыенам способы измерения связей между двумя номинальными признаками.
Проблемы возникают в том случае, если мы не фиксируем заранее указанную подтаблицу, а ставим перед собой цель, например, найти такие подтаблицы исходной таблицы сопряженности,которые обладают свойствами, отличающими их от всей таблицы (либо от других подтаблиц). Например, такие, для которых тотили иной коэффициент связи больше (меньше), чем на всей таблице(на других подтаблицах). В качестве еще одной цели можетслужить изучение того, за счет каких подсвязей формируется наша "большая" связь. Можно считать целью изучение каких-то свойств, скажем, не учителей иврачей вместе (т.е. не такого множества респондентов, которое отвечает совокупности значений одного и того же признака -в данном случае - профессии), а, например, учителей старше 50лет, работающих в гимназиях (т.е. совокупности респондентов,отвечающей набору значений разных признаков - в данном случае- профессии, места работы и возраста). Возможны и другие повороты. Рассмотрим два класса методов, определяемых выбором цели.
Первый класс методов - группа альтернатив отвечает одному признаку.
Рассматриваемый класс определяется тем, что каждая из"групп альтернатив", означенных в названии нашего параграфа,состоит из значений одного признака (скажем, это разные наименования профессий, т.е. разные значения признака"профессия"). Исходная информация в таком случае представляетсобой таблицу сопряженности между двумя признаками, отвечающими нашим двум "группам альтернатив".
Здесь можно было бы, в свою очередь, говорить о возможности выделения двухподклассов задач.
Первый подкласс – математико-статистический. Речь идет о выяснении того, из каких компонент состоит величина "Хи-квадрат", вычисленная для рассматриваемой частотнойтаблицы, или, как мы будем говорить, о разложении этой величины на составные части, позволяющие определить, какой вклад внее осуществляют разные фрагменты таблицы сопряженности. Для решения соответствующих задач существуют строгие правила перенесения результатов с выборки на генеральную совокупность и т.д. Этот подкласс будет подробно рассмотрен нами в следующем параграфе.
Второй подкласс состоит из типичных задач анализа данных. Для них не разработан тот "антураж", котороготребуют строгие каноны математической статистики. Об этом подклассе скажем несколько слов здесь.
Будем полагать, чтонас не интересует разложение 
, т.е. не интересует выяснениетого, из чего состоит эта величина, каков вклад в нее тех илииных фрагментов таблицы сопряженности. Зададимся более простойцелью: поиском в этой таблице таких ее подтаблиц, которые отличаются наиболее сильной связью (понимаемой в каком-нибудь изизвестных нам смыслов) между определяющими эти подтаблицы группами альтернатив. Ясно, что решение этой задачисводится к простому перебору всевозможных подтаблиц и вычислению отвечающих им показателей связи. Большой науки дляэтого не требуется. Мы не будем больше рассматривать эту задачу (и, стало быть второй подкласс методов), отметив, однако, ее важность для социолога.
Второй класс методов – группа альтернатив отвечает разным признакам.
Методы этого класса также относятся к типичным методаманализа данных, поскольку для них не разработан строгий математико-статистический подход. О них пойдет речь в п. 2.5.3. Мы увидим, что приведенное в заглавии п.2.5 название типа изучаемых связей естественным образом может быть обобщено: во многих реальных ситуациях вместозадач типа "(группа альтернатив)-(группа альтернатив)" имеетсмысл рассмотреть задачи типа "(группа альтернатив)-("поведение" респондентов)", где "поведение" может быть описано не только путем задания отвечающих рассматриваемым респондентам групп альтернатив, но и другими способами.
Вопросы для самопроверки
1. Какие возможные подходы знаете к изучению локальной связи?
2. Выход за пределы связей детерминационного анализа
3. Какие примыкающие задачи знаете к типу связи "группа альтернатив–группа альтернатив"?
Лекция 15.
Анализ связей типа "признак – группа признаков": номинальный регрессионный анализ (НРА).
Общая постановка задачи.
Мы подчеркивали,что в большинстве реальных задач исследователь не должен следовать ставшему традиционным ограничению круга используемыхматематических методов только известными коэффициентами парнойсвязи. При этом описывалось две совокупности факторов, обусловливающих необходимость перехода к другим методам.
Во-первых, имеет смысл "рассыпать" все рассматриваемыепризнаки на отдельные альтернативы и затем, "склеивая" их разными способами, искать такие сочетания значений исходных признаков, которые определяют те или иные связи, то или иное "поведение" респондентов (анализ фрагментов таблиц сопряженности,алгоритмы последовательных разбиений типа и т.д. ).
Во-вторых, имеет смысл объединять отдельные признаки другс другом, искать такие их сочетания, которые в каком-то смысле детерминируютдругие признаки и их сочетания (как мы увидим ниже, в регрессионном анализе речь пойдет о детерминации среднего уровня этих “других” признаков). К соответствующим рассмотрениям мы и перейдем в настоящем параграфе. Проанализируем тугруппу методов (или задач, мы говорили о том, что задачи длянас в определенном смысле отождествляются с методами), котораяпри классификации задач была символически обозначена нами какметоды типа "признак-(группа признаков)". Сюда относится регрессионный анализ, к рассмотрению которого мы и переходим.
| Рассыпание признаков на отдельные альтернативы |
| Объединение признаков друг с другом |
| Признак-признак |
Рис. 1. Схематичное выражение причин, обусловливающих необходимость перехода от традиционных коэффициентов парной связи к другим методам анализа связей
Сначала для простоты изложения рассмотрим случай, когда унас имеется только два признака – X и Y - и нас интересует зависимость между ними. Другими словами, сначала предположим,что наша "группа признаков" состоит из одного признака – X(потом перейдем к случаю, когда вместо одного X фигурируютнесколько признаков). Мы знаем, что о связи между признакамиговорит соответствующий коэффициент корреляции: чем ближе значение модуля этого коэффициента к 1, тем более сильна этасвязь, т.е. тем с большей уверенностью мы можем полагать, чтос ростом значений одного признака растут (если коэффициенткорреляции положителен) или убывают (если коэффициент корреляции отрицателен) значения другого (напомним, что коэффициент корреляции измеряет линейную связь междупеременными; отметим, однако, что приводимые рассуждения справедливы и длядругих коэффициентов связи, например, для корреляционного отношения, дающего возможность оценить криволинейную связь). Нопри этом мы совершенно не можем сказать о том, в какой степенивозрастет значение Y, если значение X увеличится, скажем, на1. А ситуации здесь могут быть весьма разными.
Приведем пример, рассмотрев зависимостьмежду производственным стажем человека и его зарплатой. Предположим, что мы имеем дело с двумя крайними ситуациями, отраженными на рисунках 21а и 21б. В обоих случаях соответствующие коэффициенты корреляции близки к 1 (обе совокупности
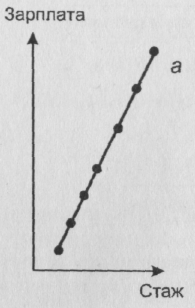
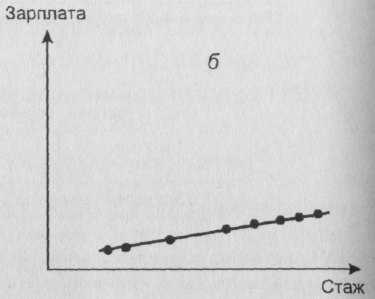
Рис. 2. Примеры сильных линейных связей, определяющих разный прогноз
точек-объектовлежат на прямых линиях, отвечающих нашей зависимости). На первом из них прямая идет резко вверх. Поэтому даже при небольшом увеличении X признак Y резко возрастет. В случае женаличия связи, изображенной на втором рисунке, прямая близка к горизонтали. Поэтому даже при значительномросте X значение Y почти не изменится. Другими словами, на основании наших двух картинок мы получим прогнозы совершенноразличного характера. И совершенно ясно, что этого никак нельзя узнать лишь на основе вычисления соответствующих коэффициентов корреляции.
Итак, для того, чтобы делать прогноз о том, как изменитсязначение Y при том или ином изменении значения X, нам желательнознать, как говорят, форму связи между этими переменными, т.е.желательно найти функцию вида Y = f (X). Подчеркнем, что отношение между X и Y несимметрично: речь идет именно о зависимости второй переменной от первой, именно о возможности прогнозазначения Y от X, а не наоборот.
В данном случае для обозначения X и Y используются те же термины, о которых шла речь в начале п. 2.5.3.1. Однако для той ситуации, когда речь идет о нахождении формы зависимости Y от X, употребляется еще несколько пар терминов: независимые переменные называют входными, экзогенными, внешними, а зависимая – выходной, эндогенной, внутренней. Представляется важным правильное понимание причин использования такой терминологии.
Поиск функции f предполагает разработку определенной модели связи между переменными, опирающуюся на априорные знания исследователя (так, ниже мы будем говорить в основном о линейной модели, о линейном регрессионном анализе). Найденная с помощью регрессионной техники зависимость – это тоже некоторая модель реальности - модель, в соответствии с которой и находятся значения Y на основе информациио значениях признака X.
Независимые признаки (X) потому и можно назвать независимыми, что они не зависят от этой модели. Эти признаки как бы поступают на ее “вход”, являются внешними по отношению к ней, берутся “со стороны”. Они определяют конкретный вид искомой зависимости, но не определяются ею. Прогнозируемые же значения зависимой переменной (Y) полностью определяются моделью (то, насколько они близки к реальности, зависит от качества модели), служат ее “выходом”, являются ее порождением. Они внутренне по отношению к ней.
Вопросы для самопроверки
1. Две совокупности факторов, обусловливающих необходимость перехода к другим методам.
2. Назовите сильные линейные связи, определяющих разный прогноз
[1] Gulliksen Н . Theory of Mental Tests. N. Y., 1950, р. 2.
Дата: 2019-03-05, просмотров: 844.
