Описательная статистика позволяет обобщать первичные результаты, полученные при наблюдении или в эксперименте. Процедуры здесь сводятся к группировке данных по их значениям, построению распределения их частот, выявлению центральных тенденций распределения (например, средней арифметической) и, наконец, к оценке разброса данных по отношению к найденной центральной тенденции.
Гипотетический эксперимент. Влияние потребления марихуаны на глазодвигательную координацию и время реакции
На группе из 30 добровольцев-студентов и студенток, курящих обычные сигареты, но не марихуану, — был проведен опыт по изучению глазодвигательной координации. Задача испытуемых заключалась в том, чтобы поражать предъявляемые на дисплее движущиеся мишени, манипулируя подвижным рычагом. Каждому испытуемому были предъявлены 10 последовательностей из 25 мишеней.
Для того чтобы установить исходный уровень, рассчитали среднее число попаданий из 25, а также среднее время реакции для 250 попыток. Далее группа была разделена на две подгруппы как можно более равным образом. Семь девушек и восемь юношей из контрольной группы получили сигарету с обычным табаком и сушеной травой, дым от которой напоминал по запаху дым марихуаны. В отличие от этого семь девушек и восемь юношей из опытной (экспериментальной) группы получили сигарету с табаком и марихуаной. Выкурив сигарету, каждый испытуемый снова был подвергнут тесту на. глазодвигательную координацию.
В табл. 1 и 2 представлены средние результаты обоих измерений для испытуемых той и другой группы до и после воздействия.
Таблица 1. Результативность испытуемых контрольной и опытной групп (среднее число пораженных мишеней из 25 в 10 сериях испытаний)
Распределение частот (числа пораженных мишеней)
Уже при первом взгляде не полученые ряды можно заметить, что многие данные принимают одни и те же значения, причем одни значения встречаются чаще, а другие — реже. Поэтому было бы интересно вначале графически представить распределение различных значений с учетом их частот. При этом получают следующие столбиковые диаграммы:
Контрольная группа
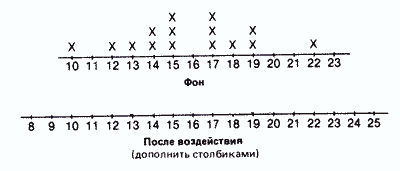
Опытная группа
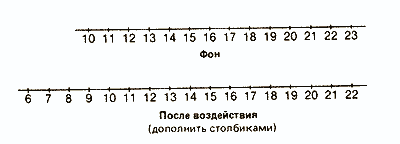
Такое распределение данных по их значениям дает нам уже гораздо больше, чем представление в виде рядов. Однако подобную группировку используют в основном лишь для качественных данных, четко разделяющихся на обособленные категории.
Что касается количественных данных, то они всегда располагаются на непрерывной шкале и, как правило, весьма многочисленны. Поэтому такие данные предпочитают группировать по классам, чтобы яснее видна была основная тенденция распределения.
Такая группировка состоит в основном в том, что объединяют данные с одинаковыми или близкими значениями в классы и определяют частоту для каждого класса. Способ разбиения на классы зависит от того, что именно экспериментатор хочет выявить при разделении измерительной шкалы на равные интервалы. Например, в нашем случае можно сгруппировать данные по классам с интервалами в две или три единицы шкалы:
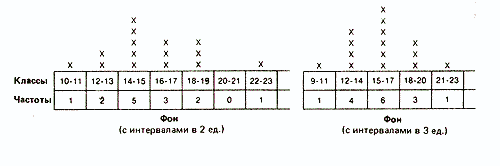
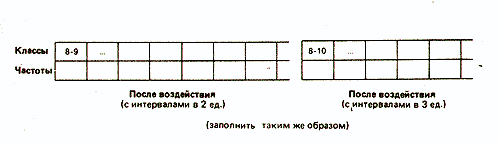
Выбор того или иного типа группировки зависит от различных соображений. Так, в нашем случае группировка с интервалами между классами в две единицы хорошо выявляет распределение результатов вокруг центрального «пика». В то же время группировка с интервалами в три единицы обладает тем преимуществом, что дает более обобщенную и упрощенную картину распределения, особенно если учесть, что число элементов в каждом классе невелико. При большом количестве данных число классов по возможности должно быть где-то в пределах от 10 до 20, с интервалами до 10 и более. Именно поэтому в дальнейшем мы будем оперировать классами в три единицы.
Опытная группа
Данные, разбитые на классы по непрерывной шкале, нельзя представить графически так, как это сделано выше. Поэтому предпочитают использовать так называемые гистограммы способ графического представления в виде примыкающих друг к другу прямоугольников:
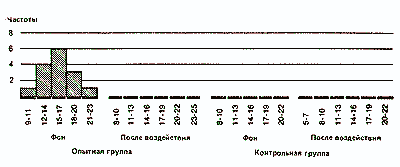
Наконец, для еще более наглядного представления общей конфигурации распределения можно строить полигоны распределения частот. Для этого отрезками прямых соединяют центры верхних сторон всех прямоугольников гистограммы, а затем с обеих сторон «замыкают» площадь под кривой, доводя концы полигонов до горизонтальной оси (частота = 0) в точках, соответствующих самым крайним значениям распределения. При этом получают следующую картину:

Если сравнить полигоны, например, для фоновых (исходных) значений контрольной группы и значений после воздействия для опытной группы, то можно будет увидеть, что в первом случае полигон почти симметричен (т.е. если сложить полигон вдвое по вертикали, проходящей через его середину, то обе половины належатся друг на друга), тогда как для экспериментальной группы он асимметричен и смещен влево (так что справа у него как бы вытянутый шлейф).
Полигон для фоновых данных контрольной группы сравнительно близок к идеальной кривой, которая могла бы получиться для бесконечно большой популяции. Такая кривая — кривая нормального распределения - имеет колоколообразную форму и строго симметрична. Если же количество данных ограничено (как в выборках, используемых для научных исследований), то в лучшем случае получают лишь некоторое приближение (аппроксимацию) к кривой нормального распределения.
Если вы построите полигон для фоновых значений опытной группы и значений после воздействия для контрольной группы, то вы наверняка заметите, что так же будет обстоять дело и в этих случаях.
Дата: 2019-03-05, просмотров: 484.