| Испытуемые | Число пораженных мишеней в серии | Средняя | Отклонение от средней (d) | Квадрат отклонения от средней (d2) |
| 1 2 3 . . . 15 | 19 10 12 . . . 22 | 15,8 15,8 15,8 . . . 15,8 | -3,2 +5,8 +3,8 . . . -6,2 | 10,24 33,64 14,44 . . . 38,44 |
| Сумма ()d2 = | 131,94 | |||
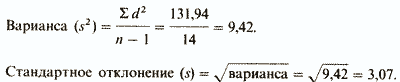
О чем же свидетельствует стандартное отклонение, равное 3,07? Оказывается, оно позволяет сказать, что большая часть результатов (выраженных здесь числом пораженных мишеней) располагается в пределах 3,07 от средней, т.е. между 12,73 (15,8-3,07) и 18,87 (15,8+3,07).
Для того чтобы лучше понять, что подразумевается под «большей частью результатов», нужно сначала рассмотреть те свойства стандартного отклонения, которые проявляются при изучении популяции с нормальным распределением.
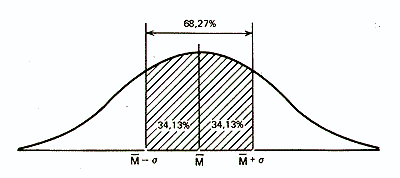
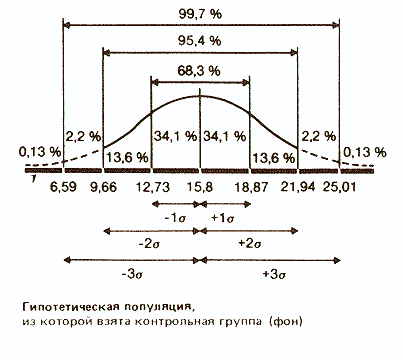
Статистики показали, что при нормальном распределении «большая часть» результатов, располагающаяся в пределах одного стандартного отклонения по обе стороны от средней, в процентном отношении всегда одна и та же и не зависит от величины стандартного отклонения: она соответствует 68% популяции (т.е. 34% ее элементов располагается слева и 34% — справа от средней):
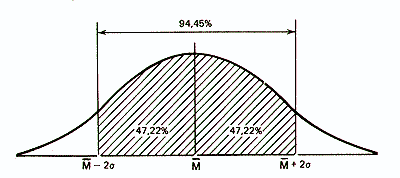
Точно так же рассчитали, что 94,45% элементов популяции при нормальном распределении не выходит за пределы двух стандартных отклонений от средней:
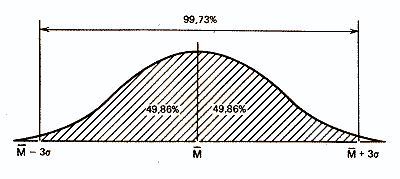
и что в пределах трех стандартных отклонений умещается почти вся популяция — 99,73%.
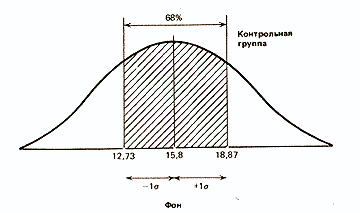
Учитывая, что распределение частот фона контрольной группы довольно близко к нормальному, можно полагать, что 68% членов всей популяции, из которой взята выборка, тоже будет получать сходные результаты, т.е. попадать примерно в 13-19 мишеней из 25. Распределение результатов остальных членов популяции должно выглядеть следующим образом:
Что касается результатов той же группы после воздействия изучаемого фактора, то стандартное отклонение для них оказалось равным 4,25 (пораженных мишеней). Значит, можно предположить, что 68% результатов будут располагаться именно в этом диапазоне отклонений от средней, составляющей 16 мишеней, т.е. в пределах от 11,75 (16-4,25) до 20,25 (16+4,25), или, округляя, 12 — 20 мишеней из 25. Видно, что здесь разброс результатов больше, чем в фоне. Эту разницу в разбросе между двумя выборками для контрольной группы можно графически представить следующим образом:
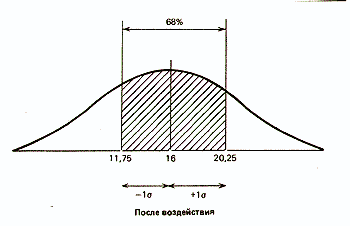
Поскольку стандартное отклонение всегда соответствует одному и тому же проценту результатов, укладывающихся в его пределах вокруг средней, можно утверждать, что при любой форме кривой нормального распределения та доля ее площади, которая ограничена (с обеих сторон) стандартным отклонением, всегда одинакова и соответствует одной и той же доле всей популяции. Это можно проверить на тех наших выборках, для которых распределение близко к нормальному, — на данных о фоне для контрольной и опытной групп.
Итак, ознакомившись с описательной статистикой, мы узнали, как можно представить графически и оценить количественно степень разброса данных в том или ином распределении. Тем самым мы смогли понять, чем различаются в нашем опыте распределения для контрольной группы до и после воздействия. Однако можно ли о чем-то судить по этой разнице — отражает ли она действительность или же это просто артефакт, связанный со слишком малым объемом выборки? Тот же вопрос (только еще острее) встает и в отношении экспериментальной группы, подвергнутой воздействию независимой переменной. В этой группе стандартное отклонение для фона и после воздействия тоже различается примерно на 1 (3,14 и 4,04 соответственно). Однако здесь особенно велика разница между средними — 15,2 и 11,3. На основании чего можно было бы утверждать, что эта разность средних действительно достоверна, т.е. достаточно велика, чтобы можно было с уверенностью объяснить ее влиянием независимой переменной, а не простой случайностью? В какой степени можно опираться на эти результаты и распространять их на всю популяцию, из которой взята выборка, т. е. утверждать, что потребление марихуаны и в самом деле обычно ведет к нарушению глазодвигательной координации?
На все эти вопросы и пытается дать ответ индуктивная статистика.
Лекции 7-11. Параметрические методы
Метод Стьюдента (f-тест)
Это параметрический метод, используемый для проверки гипотез о достоверности разницы средних при анализе количественных данных о популяциях с нормальным распределением и с одинаковой вариансой. К сожалению, метод Стьюдента слишком часто используют для малых выборок, не убедившись предварительно в том, что данные в соответствующих популяциях подчиняются закону нормального распределения (например, результаты выполнения слишком легкого задания, с которым справились все испытуемые, или же, наоборот, слишком трудного задания не дают нормального распределения).
Метод Стьюдента различен для независимых и зависимых выборок. Независимые выборки получаются при исследовании двух различных групп испытуемых (в нашем эксперименте это контрольная и опытная группы). В случае независимых выборок для анализа разницы средних применяют формулу
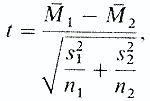
где М1 — средняя первой выборки; М2 — средняя второй выборки; s1 — стандартное отклонение для первой выборки; s2 — стандартное отклонениедля второй выборки; nl и n2 — число элементов в первой и второй выборках.
Теперь осталось лишь найти в таблице значений t (см. Приложение) величину, соответствующую n-2 степеням свободы, где n — общее число испытуемых в обеих выборках, и сравнить эту величину с результатом расчета по формуле.
Если наш результат больше, чем значение для уровня достоверности 0,05 (вероятность 5%), найденное в таблице, то можно отбросить нулевую гипотезу (Н0) и принять альтернативную гипотезу (Н1) т.е. считать разницу средних достоверной.
Если же, напротив, полученный при вычислении результат меньше, чем табличный (для n-2 степеней свободы), то нулевую гипотезу нельзя отбросить и, следовательно, разница средних недостоверна.
В нашем эксперименте с помощью метода Стьюдента для независимых выборок можно было бы, например, проверить, существует ли достоверная разница между фоновыми уровнями (значениями, полученными до воздействия независимой переменной) для двух групп. При этом мы получим:

Сверившись с таблицей значений t, мы можем прийти к следующим выводам: полученное нами значение t=0,53 меньше того, которое соответствует уровню достоверности 0,05 для 26 степеней свободы ()= 28); следовательно, уровень вероятности для такого t будет выше 0,05 и нулевую гипотезу нельзя отбросить; таким образом, разница между двумя выборками недостоверна, т. е. они вполне могут принадлежать к одной популяции.
Сокращенно этот вывод записывается следующим образом:
t=0,53; =28; р>0,05; недостоверно.
Как уже говорилось, поскольку объем выборок в данном случае невелик, а результаты опытной группы после воздействия не соответствуют нормальному распределению, лучше использовать непараметрический метод, например U-тест Манна-Уитни.
Однако наиболее полезным t-тест окажется для нас при проверке гипотезы о достоверности разницы средней между результатами опытной и контрольной групп после воздействия. Попробуйте сами найти для этих выборок значения и сделать соответствующие выводы.
Степени свободы
Для того чтобы свести к минимуму ошибки, в таблицах критических значений статистических критериев в общем количестве данных не учитывают те, которые можно вывести методом дедукции. Оставшиеся данные составляют так называемое число степеней свободы, т. е. то число данных из выборки, значения которых могут быть случайными.
Так, если сумма трех данных равна 8, то первые два из них могут принимать любые значения, но если они определены, то третье значение становится автоматически известным. Если, например, значение первого данного равно 3, а второго -1, то третье может быть равным только 4. Таким образом, в такой выборке имеются только две степени свободы. В общем случае для выборки в n данных существует п-1 степень свободы.
Если у нас имеются две независимые выборки, то число степеней свободы для первой из них составляет n1-1, а для второй — n2-1. А поскольку при определении достоверности разницы между ними опираются на анализ каждой выборки, число степеней свободы, по которому нужно будет находить критерий t в таблице, будет составлять (n1+n2)-2.
Если же речь идет о двух зависимых выборках, то в основе расчета лежит вычисление суммы разностей, полученных для каждой пары результатов (т.е., например, разностей между результатами до и после воздействия на одного и того же испытуемого). Поскольку одну (любую) из этих разностей можно вычислить, зная остальные разности и их сумму, число степеней свободы для определения критерия t будет равно n-1.
Дата: 2019-03-05, просмотров: 552.