Итак, мы получили частотное распределение значений рассматриваемого признака, т.е. выборочное представление изучаемой одномерной случайной величины. Конечно, анализ этого распределения может много дать социологу. Именно с расчета таких распределений для всех рассматриваемых признаков (так называемых “линеек”) он обычно и начинает анализ данных. Каждое распределение представляет собой своеобразное описание изучаемой совокупности объектов (респондентов). Такие описания позволяют исследователю лучше сориентироваться в проблематике, скорректировать перечень проверяемых гипотез, уточнить априорные представления об объекте и предмете исследования. Но этим анализ каждого одномерного распределения обычно не ограничивается.

Оказывается, что даже для одномерных случайных величин можно найти целый ряд статистических закономерностей. Конечно здесь они довольно примитивны (скажем, мы не можем говорить о связях между переменными), но все же это - статистические закономерности. В первую очередь мы имеем в виду так называемые меры средней тенденции, среди которых (в математической статистике известно бесконечное количество таких мер, им посвящена довольно обширная литература, см., например, [Джини, 1970]). в социологии наиболее часто используются математическое ожидание, мода и квантили (наиболее употребительным квантилем является медиана). Их мы и рассмотрим, полагая, что необходимость использования этих мер социологом очевидна. Подчеркнем лишь, что каждая из этих мер – некоторое значение (единственное!) рассматриваемого признака, которое должно характеризовать, как бы подменять, всю нашу совокупность. И социолог должен проявлять повышенное внимание к тому, чтобы с содержательной точки зрения такая подмена была оправданной.

Напомним, что названные средние являются параметрами распределения вероятностей. Не будем давать их строгого определения для генеральной совокупности. Опишем лишь то, как они измеряются для выборки. Говоря более грамотно, мы покажем, каковы выборочные точечные оценки указанных параметров, или, что то же самое, опишем способы расчета отвечающих этим параметрам выборочных статистик. (Напомним, что выборочные оценки параметров распределения делятся на точечные, когда для выборочных данных находится одно значение, служащее оценкой генерального параметра, и интервальные, когда на базе выборочной точечной оценки параметра строится так называемый доверительный интервал. Определенная на выборке переменная, значениями которой служат точечные оценки какого-либо параметра, называется статистикой, отвечающей этому параметру. Соответствующий материал обычно изучается в курсе математической статистики; см. также [Гласс, Стэнли, 1976; Статистические методы ..., 1979] .)

Все описываемые ниже меры средней тенденции являются "хорошими" выборочными точечными оценками генеральных параметров (напомним, что "хорошей" оценкой в математической статистике называются оценки, являющиеся несмещенными, состоятельными, эффективными; не будем напоминать, что это такое; отметим только, что выполнение указанных свойств

дает исследователю возможность с наибольшей вероятностью избежать сильного отклонения наблюденного значения статистики от соответствующего генерального параметра).

Пусть x₁, x₂, ..., x_N – выборочные значения рассматриваемого признака (N – объем выборки). Статистикой, отвечающей математическому ожиданию (дающей “хорошие”. точечные выборочные оценки этого параметра; это также – материал курса математической статистики) является знакомое всем среднее арифметическое значение признака:

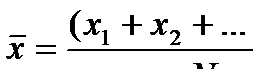
Среднее арифметическое значение признака, вычисленное для какой-либо группы респондентов, чаще всего интерпретируется как значение для наиболее типичного для этой группы человека, это среднее значение как бы служит "олицетворением" этой группы (по качеству, связанному с рассматриваемым признаком). Однако бывают случаи, когда подобная интерпретация среднего арифметического несостоятельна. Ниже мы рассмотрим некоторые из них.

Напомним, что квантиль – это такое значение признака q, которое делит диапазон его изменения на две части так, чтобы отношение числа элементов выборки, имеющих значение признака, меньшее q, к числу элементов, имеющих значение признака, большее q, было равно заранее заданной величине. Среди всех возможных квантилей обычно выделяют определенные семейства. Квантили одного семейства делят диапазон изменения признака на заданное число равнонаполненных частей. Семейство определяется тем, сколько частей получается. Наиболее популярными квантилями являются квартили, разбивающие диапазон изменения признака на 4 равнонаполненные части; децили - на 10 равнонаполненных частей; процентили – на 100 частей. Символически эти определения можно изобразить следующим образом.

Квартили:

Децили:

Процентили:

Рис. 2. Иллюстрация сущности наиболее употребительных квантилей.

Величина процента, указанная под интервалом означает долю объектов выборки, попавших в этот интервал.

Разного рода квантилями социолог пользуется очень часто. Нередко они упоминаются в средствах массовой информации (однако при этом сами термины "квантиль", "квартиль" и т.д. при этом не используются). Так, в газетах пишут о том, что, например, 10% наиболее богатых "россиян" имеют месячный доход свыше 100 тысяч рублей, а 10% наиболее бедных – ниже 300 рублей. Ясно, что 100 тысяч рублей – это девятый дециль D₉, а 300 рублей – это первый дециль D₁.

Медианой называется Мe = Q₂ = D₅ = Р₅₀.

Нетрудно видеть, что так определенная выборочная медиана – это значение рассматриваемого признака, которое делит отвечающий этому признаку вариационный ряд (т.е. последовательность значений признака, расположенных в порядке их возрастания) пополам. Иначе говоря, медиана обладает тем свойством, что половина всех выборочных значений признака меньше нее, а половина – больше. "Правомочность" медианы в качестве представителя анализируемой группы респондентов представляется очевидной. Для того, чтобы это почувствовать, достаточно "взглянуть", скажем, на две группы, в одной из которых медиана признака "доход" равна 500 рублей, а в другой – 5000 рублей. Ясно, что вторая группа "в среднем" гораздо богаче первой.

Обычно, построив вариационный ряд, полагают, что при нечетном числе элементов в выборке медиана равна центральному члену ряда, а при четном – точке, отвечающей середине расстояния между двумя центральными членами.

Нетрудно видеть, что вычисление медианы имеет смысл только для порядкового признака (и, конечно, для интервального, поскольку любая интервальная шкала является порядковой). Это представляется очевидным: для “чисто” номинальной шкалы (т.е. для такой, при использовании которой мы не ставим своей целью отображение какого бы то ни было эмпирического отношения порядка в числовое) само выражение “объект обладает значением признака, меньшим, чем медиана” становится бессмысленным. Понятия “больше” или “меньше” в этой ситуации не существуют

Вопросы для самопроверки

1. Каковы основные значения одномерного частотного распределения?

2. Среднее арифметическое значение признака.

Лекция 9.