Семейство коэффициентов, к рассмотрению которых мы переходим, основаны на такой модели связи, которая очень близка по своему содержательному смыслу к прогнозным моделям. В основе этих коэффициентов также лежит сравнение безусловного распределения с условными (условие - фиксация значения независимосго признака Х). Но сравнение это ведется не с точки зрения того, насколько при переходе от безусловного распределения к условным меняется качество возможного прогноза, а с точки зрения изучения изменения степени неопределенности рассматриваемых распределений. Здесь мы, как и в п. 1.3.5, вступаем в область теории информации и будем использовать ее терминологию.

Вернемся к рассмотренному нами в п. 1.3.5 раздела 1 понятию энтропии.

По аналогии с энтропией распределения одного признака, определяется энтропия двумерного распределения:

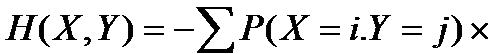
Точка внутри скобок означает конъюнкцию соответствующих событий, одновременной их выполнение. Если ввести обозначения, аналогичные использованным выше: 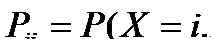, то же соотношение запишется в виде:

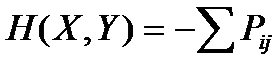
Точно так же можно определить энтропию любого многомерного распределения.

Необходимо дать определение еще одного очень важного для нас понятия – т.н. условной энтропии:

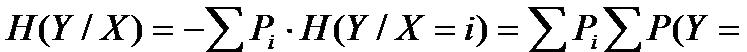(3)

Можно доказать следующие свойства энтропии.

H (X,Х) = Н (Х);       H (X,Y) = Н (Х) + Н (Y/Х);        H (X,Y) £ Н (Х) + Н (Y);

равенство в последнем соотношении появляется только тогда, когда X и Y статистически независимы, т.е. когда выполняется уже обсужденное нами соотношение: Р_ij = Р_i × Р_j..

В определенном смысле противоположным понятию энтропии является понятие информации, к рассмотрению которого мы переходим.

(Отметим, что говоря об информации в сочетании с энтропией, мы вступаем в сферу мощного научного направления – теории информации. Решающим этапом в становлении этой теории явилась публикация ряда работ К.Шеннона)

Приобретение информации сопровождается уменьшением неопределенности, поэтому количество информации можно измерять количеством исчезнувшей неопределенности, т.е. степенью уменьшения энтропии. Ниже речь пойдет об информации, содержащейся в одном признаке (случайной величине) относительно другого признака. Поясним смысл этого понятия более подробно, по существу используя другой язык для описания того же, о чем шла речь выше [Яглом, Яглом, 1980. С. 78].

Вернемся к величине Н(Y), характеризующей степень неопределенности распределения Y или, говоря несколько иначе, степень неопределенности опыта, состоящего в том, что мы случайным образом отбираем некоторый объект и измеряем для него величину Y.

Если Н(Y)=0, то исход опыта заранее известен. Большее или меньшее значение Н(Y) означает большую или меньшую проблематичность результата опыта. Измерение признака Х, предшествующее нашему опыту по измерению Y, может уменьшить количество возможных исходов опыта и тем самым уменьшить степень его неопределенности. Для того, чтобы результат измерения Х мог сказаться на опыте, состоящем в измерении Y, необходимо, чтобы упомянутый результат не был известен заранее. Значит, измерение Х можно рассматривать как некий вспомогательный опыт, также имеющий несколько возможных исходов. Тот факт, что измерение Х уменьшает степень неопределенности Y, находит свое отражение в том, что условная энтропия опыта, состоящего в измерении Y, при условии измерения Х оказывается меньше (точнее, не больше) первоначальной энтропии того же опыта. При этом, если измерение Y не зависит от измерения Х, то сведения об Х не уменьшают энтропию Y, т.е. Н(Y/Х) = Н (Y). Если же результат измерения Х полностью определяет последующее измерение Y, то энтропия Y уменьшается до нуля:

Н(Y/Х) = 0.

Таким образом, разность

I(X,Y) = Н(Y) – Н(Y/Х)                                                                                                     (4)

указывает, насколько осуществление опыта по измерению Х уменьшает неопределенность Y, т.е. сколько нового мы узнаем об Y, произведя измерение Х. Эту разность называют количеством информации относительно Y, содержащейся в Х (в научный обиход термин был введен Шенноном).

Приведенные рассуждения о смысле понятия информации очевидным образом отвечают описанной выше логике сравнения безусловного и условных распределений Y. В основе всех информационных мер связи (а о них пойдет речь ниже) лежит та разность, которая стоит в правой части равенства (4). Но именно эта разность и говорит о различии упомянутых распределений. Нетрудно понять и то, каким образом здесь происходит усреднение рассматриваемых характеристик всех условных распределений (напомним, что в качестве характеристики распределения у нас выступает его неопределенность, энтропия). По самому своему определению (см. соотношение (3)) выражение Н(Y/Х) есть взвешенная сумма всех условных энтропий (каждому значению признака Х отвечает своя условная энтропия Y:

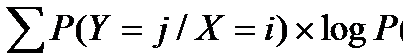
причем каждое слагаемое берется с весом, равным вероятности появления соответствующего условного распределения, т.е. вероятности Р_i . Другими словами, можно сделать вывод, что для выборки величина Н(Y/Х) - это обычное среднее взвешенное значение условных энтропий.

О возможных способах нормировки разности (Н(Y) – Н(Y/Х)) пойдет речь далее, поскольку рассматриемые ниже коэффициенты именно этой нормировкой фактически и отличаются друг от друга.

В заключение настоящего параграфа опишем некоторые свойства информации.

I(X,Y) – функция, симметричная относительно аргументов, поскольку, как нетрудно показать, имеет место соотношение:

I(X,Y) = Н(Х) + Н(Y) – Н(Х,Y),

а функция Н(Х, Y) симметрична по самому своему определению. Другими словами, количество информации, содержащейся в Х относительно Y, равно количеству информации в Y относительно Х, т.е. соотношение (4) эквивалентно соотношению

I(X,Y) = Н(Х) – Н(Х/Y),

Перейдем к описанию мер связи, основанных на понятии энтропии.