Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Раздел 3. Линейная алгебра и теория вероятностей

 

Электронная презентация – это групповое исследовательское задание. Электронная презентация разрабатывается группой студентов (2-3 чел.) в программе MS PowerPoint в соответствии с методическими рекомендациями по ее подготовке.

В процессе работы над презентацией студентам необходимо спланировать информационный поиск. Рекомендуется воспользоваться Федеральным государственным образовательным стандартом по специальности (в котором можно найти требования к специалисту и содержание учебной дисциплины Математика), изучить техническую литературу и современные научные разработки в области будущей профессиональной деятельности, актуальную нормативно-правовую документацию по специальности, а также самостоятельно подобрать литературу и другие источники, в том числе Интернет-ресурсы.

После изучения источников и отбора материала по выбранной теме информацию необходимо систематизировать. В презентацию студенты включают небольшие тематические задач (найденные или самостоятельно составленные) и приводят их решение.

Электронная презентация сдается преподавателю в указанные им сроки. Защита презентации проводится в устной форме в рамках теоретических занятий. При подготовке выступления по презентации студентам можно руководствоваться рекомендациями к подготовке устного сообщения.

Оценка электронной презентации осуществляется по следующим критериям: содержательный, логический, речевой, психологический, соблюдения дизайн-эргономических требований. При проведении консультаций и на защите презентации преподавателю необходимо обратить внимание на вклад каждого студента в выполнение группового задания, его анализ результатов своей деятельности и осознания степени персональной ответственности.

 

Тема презентаций: Теория вероятностей и математическая статистика в моей будущей профессии

 

Справочный материал

Теория вероятностей и математическая статистика находит широкое применение в машиностроении, например, при проведении контроля соответствия качества деталей требованиям технической документации.

 

Форма выполнения задания: внеаудиторная самостоятельная работа студентов.

В период разработки электронных презентаций преподаватель проводит индивидуальные консультации для студентов

 

Время на выполнение: 12 часов

ОЦЕНОЧНОЕ СРЕДСТВО № 18

КОМПЛЕКТ ЗАДАНИЙ ДЛЯ КОНТРОЛЬНОЙ работы

Раздел 3. Линейная алгебра и теория вероятностей

 

Вариант 1

1. Производительности трех станков, обрабатывающих одинаковые детали, относятся как 1:3:6. Из нерассортированной партии обработанных деталей взяты наудачу две. Какова вероятность того, что: а) одна из них обработана на 3-м станке; б) обе обработаны на одном станке?
2. У сборщика имеются 10 деталей, мало отличающихся друг от друга, из них четыре – первого, по две – второго, третьего и четвертого видов. Какова вероятность того, что среди шести взятых одновременно деталей три окажутся первого вида, два – второго и одна – третьего?
3. Прибор, работающий в течение времени t, состоит из трех узлов, каждый из которых независимо от других может за это время выйти из строя. Неисправность хотя бы одного узла выводит прибор из строя целиком. Вероятность безотказной работы в течение времени t первого узла равна 0,9, второго – 0,95, третьего – 0,8. Найти вероятность того, что в течение времени t прибор выйдет из строя.
4. Вся продукция цеха проверяется двумя контролерами, причем первый контролер проверяет 55% изделий, а второй – остальные. Вероятность того, что первый контролер пропустит нестандартное изделие, равна 0,01, второй – 0,02. Взятое наудачу изделие, маркированное как стандартное, оказалось нестандартным. Найти вероятность того, что это изделие проверялось вторым контролером.
5. Контролер ОТК, проверив качество 20 изготовленных деталей, установил, что 16 из них стандартные, а остальные имеют дефекты. Найти вероятность того, что среди взятых наудачу из этой партии трех деталей: а) одна будет иметь дефект; б) две будут иметь дефект.
6. Случайная величина Х задана законом распределения:

2	5	10
0,3	0,6	0,1

Найти:

а) математическое ожидание,

б) дисперсию,

в) среднее квадратичное отклонение этой случайной величины Х.

Вариант 2

1. К распределительному устройству подключено три потребителя с номинальной мощностью 20, 15 и 5 кВт. Вероятность включенного состояния потребителей равна Р₁ = 0,6, Р₂ = 0,7; Р₃ = 0,5. Определить вероятность того, что нагрузка на распределительном устройстве составит 40 кВт.
2. Прибор состоит из двух узлов: работа каждого узла безусловно необходима для работы прибора в целом. Надежность (вероятность безотказной работы в течение времени t) первого узла равна 0,8, второго – 0,9. Прибор испытывался в течение времени t, в результате чего обнаружено, что он вышел из строя (отказал). Найти вероятность того, что отказал только первый узел, а второй исправен.
3. Эксперт оценивает качественный уровень трех видов изделий по потребительским признакам. Вероятность того, что изделию первого вида будет присвоен знак качества, равна 0,7; для изделия второго вида эта вероятность равна 0,9; а для изделия третьего вида 0,8. Найти вероятность того, что знак качества будет присвоен: а) всем изделиям; б) только одному изделию; в) хотя бы одному изделию.
4. При включении зажигания двигатель начнет работать с вероятностью 0,6. Найти вероятность того, что: а) двигатель начнет работать при третьем включении зажигания; б) для запуска двигателя придется включать зажигание не более трех раз.
5. В коробке смешаны лампы одинакового размера и формы: по 100 Вт – 7 штук, по 75 Вт – 13 штук. Вынуты наудачу 3 лампы. Какова вероятность того, что: а) они одинаковой мощности; б) хотя бы две из них по 100 Вт?
6. Случайная величина Х задана законом распределения:

3	8	11
0,2	0,5	0,3

Найти:

а) математическое ожидание,

б) дисперсию,

в) среднее квадратичное отклонение этой случайной величины Х.

Вариант 3

1. Производятся испытания прибора. При каждом испытании прибор выходит из строя с вероятностью 0,8. После первого выхода из строя прибор ремонтируется; после второго признается негодным. Найти вероятность того, что прибор окончательно выйдет из строя в точности при четвертом испытании.
2. Мастер обслуживает 4 станка, работающих независимо друг от друга. Вероятность того, что первый станок в течение смены потребует внимания рабочего, равна 0,3, второй – 0,6, третий – 0,4 и четвертый – 0,25. Найти вероятность того, что в течение смены хотя бы один станок не потребует внимания мастера
3. В среднем каждое сотое изделие, производимое предприятием, дефектное. Если взять два изделия, какова вероятность, что оба окажутся исправными?
4. Завод выпускает определенного типа изделия; каждое изделие имеет дефект с вероятностью 0,7. После изготовления изделие осматривается последовательно тремя контролерами, каждый из которых обнаруживает дефект с вероятностями 0,8; 0,85; 0,9 соответственно. В случае обнаружения дефекта изделие бракуется. Определить вероятность того, что изделие: 1) будет забраковано; 2) будет забраковано: а) вторым контролером; б) всеми контролерами.
5. Среди 20 станков 8 нуждаются в срочном техническом обслуживании. Какова вероятность того, что среди выбранных одновременно наудачу 3 станков по крайней мере два нуждаются в обслуживании?
6. Случайная величина Х задана законом распределения:

4	3	7
0,1	0,4	0,5

Найти:

а) математическое ожидание,

б) дисперсию,

в) среднее квадратичное отклонение этой случайной величины Х.

Пакет преподавателя

 

Вариант 1

1.  а) Обозначим события: A_i – деталь обработана на i-м станке (i = 1, 2, 3);

В – одна из двух взятых деталей обработана на 3-м станке.

По условию

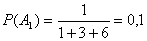
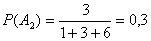
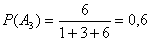
Очевидно, что B = A₁A₃+A₂A₃+A₃A₁+A₃A₂

(при этом надо учесть, что либо первая деталь обработана на 3-м станке, либо вторая).

По теоремам сложения и умножения (для независимых событий)

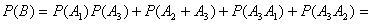
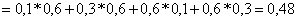
б) Пусть событие С – обе отобранные детали обработаны на одном станке.

Тогда C = A ₁ A ₁+A ₂ A ₂+A ₃ A ₃, P(C) = 0,1*0,1 + 0,3*0,3 + 0,6*0,6 = 0,46.

 

Вариант 2

4.  а) Обозначим события: А – двигатель начнет работать при каждом включении зажигания;

В – то же при третьем включении зажигания.

Очевидно, что В = 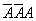, Р(В) =  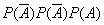= 0,4*0,4*0,6 = 0,096.

б) Пусть событие С – для запуска двигателя придется включать зажигание не более трех раз. Очевидно, событие С наступит, если двигатель начнет работать при 1-м включении, или при 2-м, или при 3-м включении, т.е. С = А+АА+ААА. Следовательно,

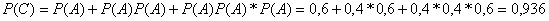
4. Программа промежуточной аттестации студентов

 

Промежуточная аттестация по дисциплине ЕН.01. Математика проводится в форме дифференцированного зачета.

При проведении промежуточной аттестации используются следующие оценочные средства:

- перечень теоретических вопросов к дифференцированному зачету,

- комплект практических заданий к дифференцированному зачету.

Перечень теоретических вопросов выдается студентам не позднее, чем за месяц до начала сессии.