I вариант	II вариант
№ 1. Вычислить следующий определенный интеграл:	№ 1. Вычислить следующий определенный интеграл:
.	.
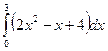№ 2. Вычислить следующий определенный интеграл методом подстановки:	№ 2. Вычислить следующий определенный интеграл методом подстановки:
.	.
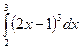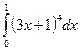№ 3. Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной следующими линиями:	№ 3. Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной следующими линиями:
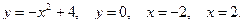
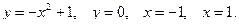
№ 4. Найти объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:	№ 4. Найти объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:
.	.
№ 5. Скорость движения точки изменяется по закону 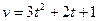 (м/с). Найти путь S, пройденный точкой за 10 с от начала движения.	№ 5. Скорость движения точки изменяется по закону 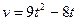 (м/с). Найти путь S, пройденный точкой за четвертую секунду.
№ 6. Сила в 2Н растягивает пружину на 4 см. Какую работу надо произвести, чтобы растянуть пружину на 4 см?	№ 6. Сила в 10 Н растягивает пружину на 2 см. Какую работу она при этом совершает?
№ 7. Сила в 60 Н достаточна, чтобы растянуть пружину на 2 см. Первоначальная длина пружины 14 см. Какую работу надо совершить, чтобы ее растянуть до 20 см?	№ 7. Деталь прогибается под нагрузкой 1,5*104 Н на 1 см. Какую работу надо затратить для деформации детали на 3 см? (Сила деформации пропорциональна величине деформации).
№ 8. Какую работу надо произвести при перемещении материальной точки на промежутке от 1 до 2 метров под действием силы, заданной законом 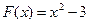.	№ 8. Тело движется неравномерно по закону .Найти его перемещение за первые 20 секунд.

Пакет преподавателя

Справочный материал

Формула для расчета перемещения неравномерного движения: .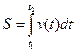

Зависимость между работой и силой выражается с помощью определенного интеграла: .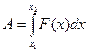

Вариант 1

7. R = 60 / 0,02 = 3000 и, следовательно,

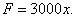
Растянуть пружину надо на 0,06 (м). Отсюда

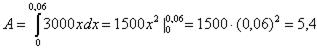
     8.

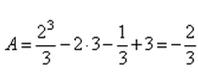
Вариант 2

6. По закону Гука сила F, растягивающая пружину, пропорциональна растяжению пружины, т.е. F = Rx. Из условия задачи R = 10 / 0,02, следовательно,

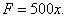
Значит,

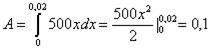
     7. F = Rx, где х – величина деформации. При х = 0,01 м имеем R:

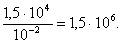
Отсюда:

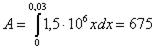
8.

Ответ: 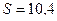 км.

ОЦЕНОЧНОЕ СРЕДСТВО № 12

РЕФЕРАТИВНОЕ ЗАДАНИЕ

Раздел 2. Комплексные числа

Форма выполнения задания: внеаудиторная самостоятельная работа студентов.

В период написания рефератов преподаватель проводит индивидуальные консультации для студентов

Время на выполнение: 6 часов

Инструкция для студентов

Уважаемые студенты! Реферат выполняется в соответствии с методическими рекомендациями по его выполнению, оформляется в бумажном варианте в соответствии со стандартом колледжа и сдается преподавателю в указанные им сроки.

В процессе работы над рефератом вам необходимо спланировать информационный поиск. Рекомендуем воспользоваться Федеральным государственным образовательным стандартом по своей специальности (в котором вы можете найти требования к специалисту и содержание учебной дисциплины Математика), изучить статьи по соответствующим разделам математики, техническую литературу и современные научные разработки в области машиностроения, актуальную нормативно-правовую документацию по специальности, а также самостоятельно подобрать литературу и другие источники, в том числе Интернет-ресурсы.

В основную часть реферата необходимо включить главу, содержащую информацию о применении понятийного и методологического аппарата теории комплексных чисел при разработке и внедрении управляющих программ обработки деталей. Например, если обрабатываемый контур представляет собой ломаную линию, то с помощью прямоугольной системы координат можно легко задать все характерные точки его профиля; однако ситуация меняется, если необходимо выполнить на плоскости сверление группы отверстий, расположенных по окружности. Если для одного отверстия координаты расположения его оси в прямоугольной системе координат можно рассчитать достаточно просто, то расчет расположения осей для всех других отверстий будет гораздо более трудоемким. В этом случае вычисления удобнее выполнять в полярной системе координат, где положение точки на плоскости определяется расстоянием (радиусом) r от точки до начала координат и углом между определенной осью координат и радиусом, проведенным в точку из начала координат.

Также в реферат включаются решения задач (из сборников или составленных самостоятельно) на выполнение действий над комплексными числами.

Защита реферата проводится в устной форме в рамках теоретических занятий. По желанию студента защита может сопровождаться электронной презентацией. При оценке реферата принимаются во внимание его исследовательский характер, грамотность изложенного материала, полнота раскрытия темы, наличие обоснованных выводов и его оформление.

Темы рефератов

1. История комплексных чисел.
2. Комплексные числа и действия над ними.
3. Тригонометрическая форма комплексного числа.
4. Показательная форма комплексного числа.
5. Применение комплексных чисел.
6. Полярная система координат и ее применение.

ОЦЕНОЧНОЕ СРЕДСТВО № 13