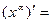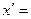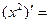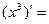Раздел 1. Математический анализ
Тема 1.1. Теория пределов
Справочный материал
В процессе проведения сборочных работ различных видов техники, обработки деталей применяются контрольно-измерительные приборы (КИП). Основной качественной характеристикой любого датчика КИП является погрешность измерения контролируемого параметра. Погрешность измерения прибора это величина расхождения между тем, что показал (измерил) датчик КИП и тем, что есть на самом деле. С точки зрения математики абсолютная погрешность может быть рассмотрена как приращение аргумента: разница между измеренным значением величины и ее действительным значением.
Приращение – это изменение величины, например, начальное значение напряжения U1=220В, конечное значение U2=120В; изменение напряжения (или дельта напряжения) будет равно ΔU=U2–U1=220В–120В=100В.
Вариант 1
1. Исследовать функцию 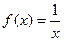 на непрерывность в точке
на непрерывность в точке 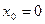 .
.
2. Вычислить приращение данной функции, если ее аргумент x получает приращение 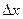 :
:
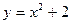 ,
, 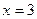 ,
, 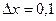 .
.
Вариант 2
1. Исследовать функцию 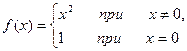 на непрерывность в точке
на непрерывность в точке 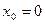 .
.
2. Вычислить приращение данной функции, если ее аргумент x получает приращение 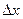 :
:
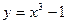 ,
, 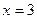 ,
, 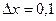 .
.
Вариант 3
1. Исследовать функцию 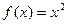 на непрерывность в точке
на непрерывность в точке 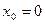 .
.
2. Вычислить приращение данной функции, если ее аргумент x получает приращение 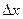 :
:
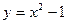 ,
, 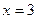 ,
, 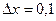 .
.
Пакет преподавателя
Вариант 1
1. Решение.
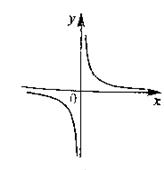
Проверим условия из определения.
1) 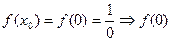 не существует, т. е. функция
не существует, т. е. функция 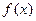 неопределенна в точке
неопределенна в точке 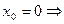 функция
функция 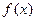 не является непрерывной в точке
не является непрерывной в точке 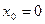 .
.
Ответ. Не является непрерывной.
Вариант 2
1. Решение.
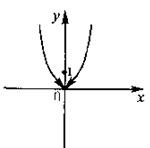
Проверим условия из определения.
1) 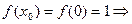 функция
функция 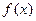 определенна в точке
определенна в точке 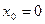 .
.
2) 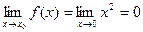 . Функция
. Функция 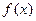 имеет конечный предел при
имеет конечный предел при 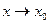 .
.
3) 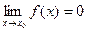 ,
, 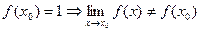 . Предел функции при
. Предел функции при 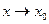 не равен значению функции в этой точке.
не равен значению функции в этой точке.
Ответ. Не является непрерывной.
Вариант 3
1. Решение.
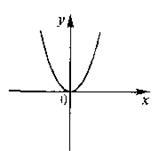
Проверим условия из определения.
1) 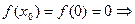 функция
функция 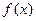 определенна в точке
определенна в точке 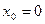 .
.
2) 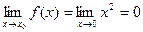 . Функция
. Функция 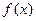 имеет конечный предел при
имеет конечный предел при 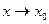 .
.
3) 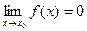 ,
, 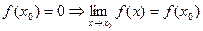 . Предел функции при
. Предел функции при 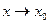 равен значению функции в этой точке.
равен значению функции в этой точке.
Ответ. Непрерывна.
ОЦЕНОЧНОЕ СРЕДСТВО № 4
КОМПЛЕКТ ЗАДАНИЙ ДЛЯ комбинированного (уплотненного) опроса
Раздел 1. Математический анализ
Тема 1.2. Производная, исследование функций с помощью производных
Перечень вопросов и задач
- Дать определение производной функции.
- В чем заключается геометрический смысл производной?
- В чем заключается физический смысл производной?
- Что такое дифференциал функции?
- Какая функция называется сложной?
- Что такое вторая производная и производные высших порядков?
- В чем заключается физический смысл второй производной?
- Сформулировать правила дифференцирования и записать производные основных элементарных функций и производную сложной функции:
| 1о. | 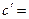
| 8о. | 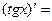
|
| 2о. |
В частности, | 9о. | 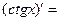
|
| 10о. | 
| ||
| 11о. | 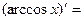
| ||
| 12о. | 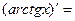
| ||
| 13о. | 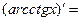
| ||
| ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ | |||
| 14о. | 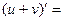
| ||
| 3о. | 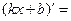
| 15о. | 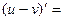
|
| 4о. |
В частности, | 16о. | 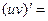
|
| 17о. | 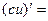
| ||
| 5о. | 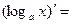 В частности,
В частности, 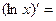
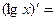
| 18о. | 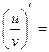 В частности,
В частности, 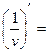
|
| 6о. | 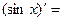
| ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ | |
| 7о. | 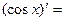
| 19о. | 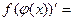
|
- Найти производные следующих функций:
а) 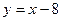 ;
;
б) 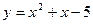 ;
;
в) 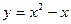 ;
;
г) 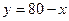 .
.
- Найти производные функций и вычислить их значения в точках
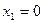 и
и 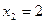 :
:
а) 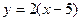 ;
;
б) 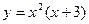 ;
;
в) 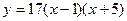 ;
;
г) 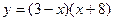 ;
;
д) 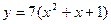 ;
;
е) 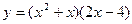 .
.
-
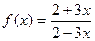 . Найти
. Найти 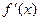 ,
, 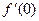 ,
, 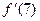 ,
, 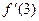 .
. -
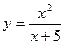 . Найти
. Найти 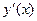 ,
, 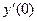 ,
, 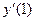 .
. - Найти производную следующей функции:
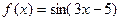 .
.
- Найти производную следующей функции:
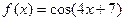 .
.
- Найти производную следующей функции:
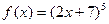 .
.
ОЦЕНОЧНОЕ СРЕДСТВО № 5
Дата: 2019-03-05, просмотров: 398.