Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Раздел 3. Линейная алгебра и теория вероятностей

Тема 3.1. Матрицы и определители

 

Справочный материал

В машиностроении широко применяется математическое моделирование. Математическая модель – приближённое описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики. Например, можно построить математическую модель сверления лазером, математическую модель работы газотурбинного двигателя, математическую модель силы резания токарной операции. Часто в качестве аппарата для построения математических моделей используются понятия линейной алгебры – системы линейных уравнений, матрицы и определители. Множество объектов рассматривают как преобразователи, для которых каждому входу соответствует некоторый выход. Так, если изучают задачу о прогибе прямолинейного стержня под действием поперечной распределенной нагрузки, то входом можно считать ее плотность, а выходом – прогиб. Решение уравнений математической модели будет являться выходом.

В процедурах, относящихся к конструкторскому аспекту проектирования, преобладает использование математических моделей, отражающих структурные свойства объекта, например его геометрическую форму, размеры, взаимное расположение элементов в пространстве, т. е. структурные модели, которые часто представляются в виде матриц.

 

Вариант 1

1. 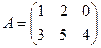, 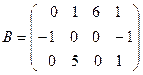. Найти .

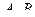2. 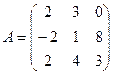, 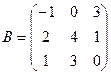. Найти C=A+B, C=2B, C=3A, C=2A-B.

 

Вариант 2

1. 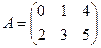, 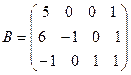. Найти .

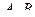2. 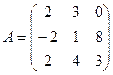, 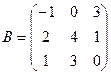. Найти C=2A, C=A-B, C=A+3B, C=A-4B.

Вариант 3

1. 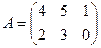, 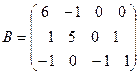. Найти .

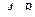2. 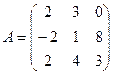, 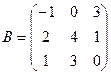. Найти C=4B, C=4A-B, C=3A+B, C=A+2B.

Пакет преподавателя

 

Вариант 1

2.  ;

     ;           ;

     .

 

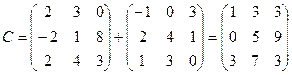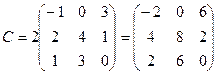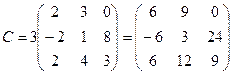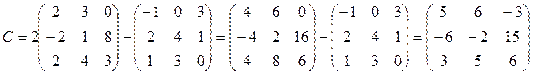Вариант 2

2.  ;

;

     ;

.

 

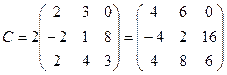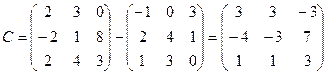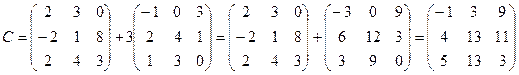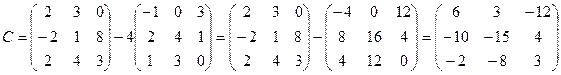Вариант 3

2.  ;

;

;

.

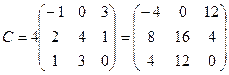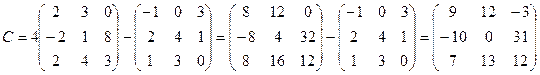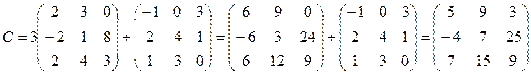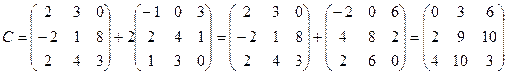ОЦЕНОЧНОЕ СРЕДСТВО № 14

КОМПЛЕКТ ЗАДАНИЙ ДЛЯ проверочной РАБОТЫ

Раздел 3. Линейная алгебра и теория вероятностей

Тема 3.1. Матрицы и определители

 

Справочный материал

В машиностроении широко применяется математическое моделирование. Математическая модель – приближённое описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики. Например, можно построить математическую модель сверления лазером, математическую модель работы газотурбинного двигателя, математическую модель силы резания токарной операции. Часто в качестве аппарата для построения математических моделей используются понятия линейной алгебры – системы линейных уравнений, матрицы и определители. Множество объектов рассматривают как преобразователи, для которых каждому входу соответствует некоторый выход. Так, если изучают задачу о прогибе прямолинейного стержня под действием поперечной распределенной нагрузки, то входом можно считать ее плотность, а выходом – прогиб. Решение уравнений математической модели будет являться выходом.

В процедурах, относящихся к конструкторскому аспекту проектирования, преобладает использование математических моделей, отражающих структурные свойства объекта, например его геометрическую форму, размеры, взаимное расположение элементов в пространстве, т. е. структурные модели, которые часто представляются в виде матриц.

 

Вариант 1

1. Вычислить определители:

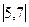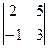а) ;    б) ;      в) .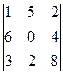

2. Вычислить определители четвертого порядка:

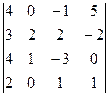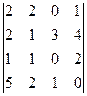а) ;   б) ;      в) .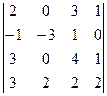

 

Вариант 2

1. Вычислить определители:

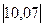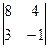а) ; б) ;      в) .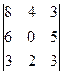

2. Вычислить определители четвертого порядка:

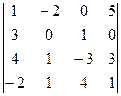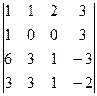а) ; б) ;    в) .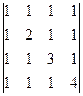

Вариант 3

1. Вычислить определители:

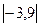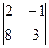а) ;  б) ;      в) .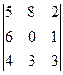

2. Вычислить определители четвертого порядка:

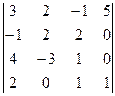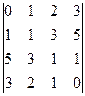а) ;  б) ;       в) .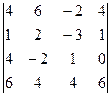

Пакет преподавателя

 

Вариант 1

2.  б) –24;   в) 5.

 

Вариант 2

2.  б) 50; в) 6.

 

Вариант 3

2.  б) –18;   в) –144.

ОЦЕНОЧНОЕ СРЕДСТВО № 15