Тема 3.2. Классическое определение вероятности
Инструкция по работе с кейсом
Уважаемые студенты!
Вашему вниманию предлагается кейс, выполняя который вы узнаете на примере исторического материала о Великой Отечественной войне, что для овладения современными военно-техническими системами и боевым мастерством совершенно необходимы математические знания.
Структура вашей работы будет следующей:
1. Внимательно изучите предложенный справочный материал кейса.
2. В микрогруппах решите тренировочную задачу, приведенную в кейсе, и представьте полученные результаты преподавателю.
3. Совместно с преподавателем определите место данного кейса в курсе Математики. Для этого ответьте на вопрос: какие математические понятия и методы используются для решении приведенной в кейсе задачи? Если в процессе деятельности вы осознаете недостаток информации, вы можете воспользоваться учебными и справочными пособиями по математике, предложенными преподавателем.
4. Решите в микрогруппах задачу для самостоятельного решения и представьте полученные результаты. Если в процессе решения вы осознаете недостаток информации, вы можете воспользоваться учебными и справочными пособиями по математике, предложенными преподавателем.
5. В микрогруппах составьте аналогичные задачи. Если в процессе составления задачи вы осознаете недостаток информации, вы можете воспользоваться учебными и справочными пособиями по математике, предложенными преподавателем. Разработайте стратегию решения данного класса задач для студентов (разбейте общую задачу на подзадачи, опишите последовательность действий – что изучить, что использовать при решении, чем руководствоваться и т.д.).
6. Представьте разработанную стратегию решения всей группе и предложите составленные вами задачи для решения другим микрогруппам.
КЕЙС № 1
Справочный материал
Большой вклад в победу над фашистской Германией в Великой Отечественной войне 1941 – 1945 гг. внесли математики. Так, только во время операций на Курской дуге было израсходовано несколько миллионов патронов для пулеметов. Однако их нужно было не только изготовить, но и проверить качество. Проверка же порой занимает больше времени, чем изготовление. Методы проверки качества боеприпасов были предложены ещё в XIX веке простым математиком Михаилом Васильевичем Остроградским, но получили развитие и широкое применение лишь в XX веке, особенно в период Великой Отечественной войны и после её окончания. Активное участие в этой работе принял академик Андрей Николаевич Колмогоров и его ученики.
Тренировочная задача
Вероятность попадания в мишень при каждом выстреле для 1-го стрелка равна 0,7, а для 2-го – 0,8. Оба они делают по одному выстрелу по мишени, а затем каждый из стрелков стреляет еще раз, если при первом сделанном им выстреле он промахнулся. Найти вероятность того, что в мишени ровно 2 пробоины.
Задача для самостоятельного решения
Вероятность изготовления изделия с браком на оборонном предприятии равна 0,04. Перед выпуском изделие подвергается упрощенной проверке, которая в случае бездефектного изделия пропускает его с вероятностью 0,96, а в случае изделия с дефектом – с вероятностью 0,05. Определить: а) какая часть изготовленных изделий выходит с предприятия; б) какова вероятность того, что изделие, выдержавшее упрощенную проверку, бракованное?
КЕЙС № 2
Справочный материал
Большой вклад в победу над фашистской Германией в Великой Отечественной войне 1941 – 1945 гг. внесли математики. Так, видная роль в деле обороны нашей Родины принадлежит выдающемуся математику академику А.Н. Крылову, чьи труды по теории непотопляемости и качки корабля были использованы нашими Военно-морскими силами. Он создал таблицы непотопляемости, в которых было рассчитано, как повлияет на корабль затопление тех или иных отсеков, какие номера отсеков нужно затопить, чтобы ликвидировать крен, и насколько это затопление может улучшить состояние корабля. Эти таблицы дали возможность спасти жизнь многих людей, сберечь большие материальные ценности.
Тренировочная задача
В пирамиде 5 винтовок, 3 из которых снабжены оптическим прицелом. Вероятность попадания для стрелка при выстреле из винтовки с оптическим прицелом равна 0.95, из обычной винтовки – 0.7. Стрелок наудачу берет винтовку и стреляет. Найти вероятность того, что мишень будет поражена.
Задача для самостоятельного решения
В сторону крейсера неприятеля подводной лодкой были выпущены 3 торпеды. Вероятность попадания первой торпеды равна 0,5, второй – равна 0,6, третьей – равна 0,8. При попадании одной торпеды вероятность того, что крейсер затонет, равна 0,3, при попадании двух торпед 0,6, а при попадании трёх торпед 1. Какова вероятность того, что неприятельский крейсер будет потоплен?
КЕЙС № 3
Справочный материал
Большой вклад в победу над фашистской Германией в Великой Отечественной войне 1941 – 1945 гг. внесли математики. Так, проблемы увеличения эффективности огня артиллерии и повышения меткости стрельбы в годы Великой Отечественной войны успешно решает академик А.Н. Колмогоров. По заданию Главного артиллерийского управления он, используя свои работы по математике в области теории вероятностей, дал определение наивыгоднейшего рассеяния артиллерийских снарядов. Математика помогла рассчитать, сколько нужно сделать одновременных выстрелов по самолёту противника для того, чтобы иметь наибольшую вероятность сбить его.
Тренировочная задача
В пирамиде 6 винтовок, 3 из которых снабжены оптическим прицелом. Вероятность попадания для стрелка при выстреле из винтовки с оптическим прицелом равна 0.9, из обычной винтовки – 0.6. Стрелок наудачу берет винтовку и стреляет. Найти вероятность того, что мишень будет поражена.
Задача для самостоятельного решения
Батарея, состоящая из 3 орудий, ведет огонь по группе, состоящей из 5 самолетов. Каждое орудие выбирает себе цель случайно и независимо от других. Найти вероятность того, что все орудия будут стрелять: а) по одной и той же цели; б) по разным целям.
КЕЙС № 4
Справочный материал
Большой вклад в победу над фашистской Германией в Великой Отечественной войне 1941 – 1945 гг. внесли математики. Так, только во время операций на Курской дуге было израсходовано несколько миллионов патронов для пулеметов. Однако их нужно было не только изготовить, но и проверить качество. Проверка же порой занимает больше времени, чем изготовление. Методы проверки качества боеприпасов были предложены ещё в XIX веке простым математиком Михаилом Васильевичем Остроградским, но получили развитие и широкое применение лишь в XX веке, особенно в период Великой Отечественной войны и после её окончания. Активное участие в этой работе принял академик Андрей Николаевич Колмогоров и его ученики.
Тренировочная задача
Два стрелка сделали по одному выстрелу в мишень. Вероятность попадания в мишень для первого стрелка равна 0,6, а для второго – 0,3. В мишени оказалась одна пробоина. Найти вероятность того, что она принадлежит первому стрелку.
Задача для самостоятельного решения
Брак в продукции военного завода вследствие дефекта А составляет 4%, а вследствие дефекта В – 3,5%. Годная продукция завода составляет 95%. Найти вероятность того что: а) среди продукции, не обладающей дефектом А, встретится дефект В; б) среди забракованной по признаку А продукции встретится дефект В.
КЕЙС № 5
Справочный материал
Большой вклад в победу над фашистской Германией в Великой Отечественной войне 1941 – 1945 гг. внесли математики. Так, видная роль в деле обороны нашей Родины принадлежит выдающемуся математику академику А.Н. Крылову, чьи труды по теории непотопляемости и качки корабля были использованы нашими Военно-морскими силами. Он создал таблицы непотопляемости, в которых было рассчитано, как повлияет на корабль затопление тех или иных отсеков, какие номера отсеков нужно затопить, чтобы ликвидировать крен, и насколько это затопление может улучшить состояние корабля. Эти таблицы дали возможность спасти жизнь многих людей, сберечь большие материальные ценности.
Тренировочная задача
В пирамиде 7 винтовок, 3 из которых снабжены оптическим прицелом. Вероятность попадания для стрелка при выстреле из винтовки с оптическим прицелом равна 0.9, из обычной винтовки – 0.6. Стрелок наудачу берет винтовку и стреляет. Найти вероятность того, что мишень будет поражена.
Задача для самостоятельного решения
Батарея из трех орудий произвела залп, причем два снаряда попали в корабль. Найти вероятность того, что первое орудие дало попадание, если вероятности попадания в цель первым, вторым и третьим орудиями соответственно равны p 1 = 0,4, p 2 = 0,3, p 3 = 0,5.
КЕЙС № 6
Справочный материал
Большой вклад в победу над фашистской Германией в Великой Отечественной войне 1941 – 1945 гг. внесли математики. Так, проблемы увеличения эффективности огня артиллерии и повышения меткости стрельбы в годы Великой Отечественной войны успешно решает академик А.Н. Колмогоров. По заданию Главного артиллерийского управления он, используя свои работы по математике в области теории вероятностей, дал определение наивыгоднейшего рассеяния артиллерийских снарядов. Математика помогла рассчитать, сколько нужно сделать одновременных выстрелов по самолёту противника для того, чтобы иметь наибольшую вероятность сбить его.
Тренировочная задача
В пирамиде 6 винтовок, 4 из которых снабжены оптическим прицелом. Вероятность попадания для стрелка при выстреле из винтовки с оптическим прицелом равна 0.95, из обычной винтовки – 0.8. Стрелок наудачу берет винтовку и стреляет. Найти вероятность того, что мишень будет поражена.
Задача для самостоятельного решения
Вероятность одного попадания в самолет неприятеля при одном залпе из двух орудий равна 0,38, а при выстреле из первого орудия вероятность попадания равна 0,8. Какова вероятность попадания при выстреле из второго орудия?
КЕЙС № 7
Справочный материал
Большой вклад в победу над фашистской Германией в Великой Отечественной войне 1941 – 1945 гг. внесли математики. Так, только во время операций на Курской дуге было израсходовано несколько миллионов патронов для пулеметов. Однако их нужно было не только изготовить, но и проверить качество. Проверка же порой занимает больше времени, чем изготовление. Методы проверки качества боеприпасов были предложены ещё в XIX веке простым математиком Михаилом Васильевичем Остроградским, но получили развитие и широкое применение лишь в XX веке, особенно в период Великой Отечественной войны и после её окончания. Активное участие в этой работе принял академик Андрей Николаевич Колмогоров и его ученики.
Тренировочная задача
Быстро вращающийся диск разделен на четное число равных секторов, попеременно окрашенных в белый и черный цвет. По диску произведен выстрел. Найти вероятность того, что пуля попадет в один из белых секторов. Предполагается, что вероятность попадания пули в плоскую фигуру пропорциональна площади этой фигуры.
Задача для самостоятельного решения
При приеме партии боеприпасов подвергается проверке половина изделий. Условие приемки – наличие брака в выборке менее 2%. Вычислить вероятность того, что партия из 100 изделий, содержащая 5% брака, будет принята.
КЕЙС № 8
Справочный материал
Большой вклад в победу над фашистской Германией в Великой Отечественной войне 1941 – 1945 гг. внесли математики. Так, видная роль в деле обороны нашей Родины принадлежит выдающемуся математику академику А.Н. Крылову, чьи труды по теории непотопляемости и качки корабля были использованы нашими Военно-морскими силами. Он создал таблицы непотопляемости, в которых было рассчитано, как повлияет на корабль затопление тех или иных отсеков, какие номера отсеков нужно затопить, чтобы ликвидировать крен, и насколько это затопление может улучшить состояние корабля. Эти таблицы дали возможность спасти жизнь многих людей, сберечь большие материальные ценности.
Тренировочная задача
В пирамиде 7 винтовок, 4 из которых снабжены оптическим прицелом. Вероятность попадания для стрелка при выстреле из винтовки с оптическим прицелом равна 0.95, из обычной винтовки – 0.7. Стрелок наудачу берет винтовку и стреляет. Найти вероятность того, что мишень будет поражена.
Задача для самостоятельного решения
Произведено три выстрела по кораблю неприятеля из орудия. Вероятность попадания при первом выстреле равна 0,75; при втором – 0,8; при третьем – 0,9. Определить вероятность того, что будет: а) три попадания; б) хотя бы одно попадание.
КЕЙС № 9
Справочный материал
Большой вклад в победу над фашистской Германией в Великой Отечественной войне 1941 – 1945 гг. внесли математики. Так, проблемы увеличения эффективности огня артиллерии и повышения меткости стрельбы в годы Великой Отечественной войны успешно решает академик А.Н. Колмогоров. По заданию Главного артиллерийского управления он, используя свои работы по математике в области теории вероятностей, дал определение наивыгоднейшего рассеяния артиллерийских снарядов. Математика помогла рассчитать, сколько нужно сделать одновременных выстрелов по самолёту противника для того, чтобы иметь наибольшую вероятность сбить его.
Тренировочная задача
В пирамиде 8 винтовок, 4 из которых снабжены оптическим прицелом. Вероятность попадания для стрелка при выстреле из винтовки с оптическим прицелом равна 0.95, из обычной винтовки – 0.8. Стрелок наудачу берет винтовку и стреляет. Найти вероятность того, что мишень будет поражена.
Задача для самостоятельного решения
Вероятность одного попадания в самолет неприятеля при одном залпе из двух зенитных орудий равна 0,46. Найти вероятность попадания при одном выстреле второго орудия, если известно, что для первой эта вероятность равна 0,7.
Пакет преподавателя
КЕЙС № 1
Тренировочная задача
Пусть события: Ai, Bi – попадание в цель соответственно 1-м, 2-м стрелком при i-м выстреле (i=1,2);
С – в мишени ровно 2 пробоины.
Событие С произойдет, если:
- у каждого стрелка по одному попаданию с первого раза;
- у 1-го стрелка – попадание (при одном выстреле), у 2-го стрелка – промах и попадание;
- у 1-го стрелка – промах и попадание, у 2-го стрелка – попадание (при одном выстреле);
- у каждого стрелка – промах и попадание после двух выстрелов.
Итак,
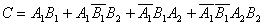
Используя теоремы сложения для несовместных и умножения для независимых событий, получим:
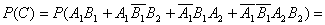
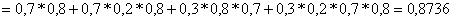
КЕЙС № 2
Задача для самостоятельного решения

КЕЙС № 5
Задача для самостоятельного решения

КЕЙС № 6
Задача для самостоятельного решения

КЕЙС № 9
Задача для самостоятельного решения
При работе над кейсом применяется групповая технология обучения, в рамках которой с помощью наблюдения за деятельностью студентов можно зафиксировать следующие поведенческие признаки:
- планирование студентами своей деятельности в рамках заданной технологии;
- обучение студентами других членов микрогрупп и всей группы рациональным приемам по организации деятельности для эффективного выполнения коллективного проекта;
- распределение студентами объема работы среди участников коллективного проекта;
- преодоление студентами кризисов взаимодействия совместно с членами группы.
Данные признаки нашли отражение в критериях оценки выполнения кейс-задания.
Кроме того, при наблюдении за выполнением студентами данного задания можно оценить, в какой мере каждый студент осознает и восполняет недостаток информации, освоенных умений и усвоенных знаний в процессе реализации деятельности, определяет стратегию решения проблемы, разбивает поставленную цель на задачи, проявляет патриотизм, анализирует полученные профессиональные знания применительно к военным технологиям.
ОЦЕНОЧНОЕ СРЕДСТВО № 17
исследовательское задание –
Дата: 2019-03-05, просмотров: 890.