6.4.1. Описание (задание) движения

На рис.60 изображено несколько тел, совершающих такое движение. Так на рис.60.а тело прикреплено к неподвижной опорной поверхности шаровым шарниром, на рис.60.б изображен двухстепенной гироскоп, а на рис.60.в – конус, катящийся по плоскости без проскальзывания.

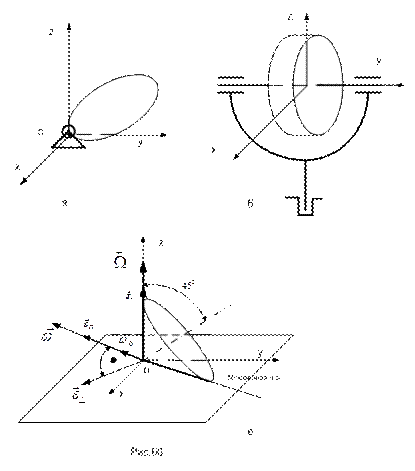
Так как расстояние между неподвижной точкой тела и любой другой остается неизменным в силу его абсолютной твердости, траектория движения любой точки лежит на сфере, радиус которой равен этому расстоянию. Отмеченная особенность и определила название движения как сферическое.

Этот тип движения тесно связан с ранее рассмотренным случаем вращения тела вокруг неподвижной оси, так как сферическое движение может быть представлено в виде непрерывной последовательности малых (элементарных) поворотов вокруг перемещающейся в пространстве оси. Эта ось называется мгновенной осью вращения тела. Скорости всех точек мгновенной оси равны нулю. Часто положение этой оси и ее движение очевидны. Так, для изображенного на рис.60.в конуса, катящегося без проскальзывания по неподвижной плоскости, мгновенной осью будет линия их соприкосновения; в процессе движения конуса эта ось вращается вокруг вертикальной оси .

Отличительная особенность этого подхода заключается в том, что понятие суммарного угла поворота лишается обычного смысла, так как элементарные повороты происходят вокруг различных положений мгновенной оси.

При таком подходе, как и в пункте 6.2.1, можно ввести в рассмотрение вектор 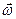 угловой скорости, направленный вдоль орта  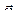мгновенной оси, т.е. 

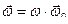                                                                                 (47)

и вектор углового ускорения

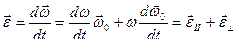 .                                  (48)

Первая из компонент вектора 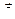 отражает изменение модуля вектора 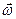; она обозначается  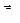 и называется параллельной составляющей углового ускорения, т.к. совпадает с направлением мгновенной оси. Вторая компонента связана с переменностью направления мгновенной оси и, как следствие, орта 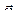; она обозначается  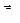и называется перпендикулярной составляющей углового ускорения (т.к. перпендикулярна орту  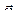мгновенной оси).

Тогда 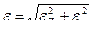.                                                              (49)

Рассмотренный подход позволяет для вычисления локальных характеристик использовать полученные ранее формулы (44) и (45):

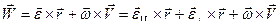                        (50)

При этом последнее слагаемое называется осестремительной составляющей ускорения, а два первых – параллельной и перпендикулярной вращательной составляющими.

В наиболее общем случае сферическое движение тела с тремя степенями свободы описывается (задается) тремя обобщенными координатами, называемыми углами Эйлера. В настоящем курсе этот подход не обсуждается.

ПРИМЕР  23. Коническое зубчатое колесо радиуса 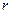 катится по неподвижному зубчатому колесу радиуса 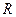; угол между осями колес составляет  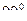(см. рис.61). Время одного оборота относительно вертикальной оси постоянно и равно Т . Найти угловую скорость  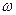и угловое ускорение  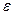колеса, а так же скорость  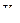и ускорение 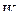его верхней точки А.

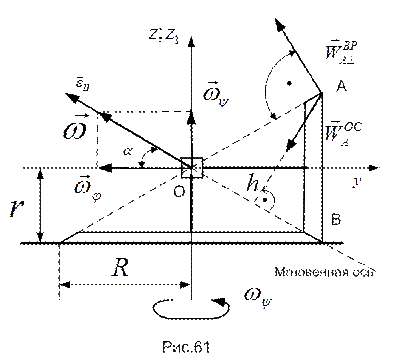
РЕШЕНИЕ. Угловая скорость прецессии колеса 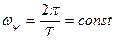. Угол нутации постоянен и равен 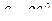, т.е. 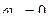. В этом случае 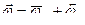. Построив соответствующий параллелограмм угловых скоростей (сторона  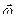известна, линия вектора 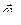совпадает с осью подвижного колеса, линия мгновенной оси проходит через две неподвижные точки – точку О и точку В контакта с неподвижным колесом), получим:

 ,  .

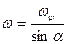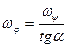При движении колеса вектор мгновенной угловой скорости поворачивается вокруг вертикальной оси, образуя коническую поверхность с углом при вершине ( 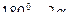); поскольку  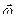и направления векторов  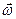и 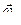 в подвижной системе осей не изменяются, не изменяется и модуль вектора 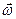. В этом случае ; .

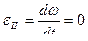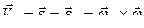Вектор углового ускорения приложен в точке О и направлен на нас перпендикулярно плоскости рисунка. Модуль углового ускорения равен  

.

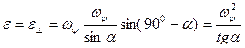Опустив из точки А на мгновенную ось перпендикуляр, найдем кратчайшее расстояние от точки до линии вектора 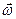 как

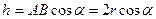. Тогда вектор скорости точки А будет направлен перпендикулярно плоскости рисунка в противоположную от нас сторону, а его модуль будет равен

 .

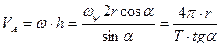Осестремаительная составляющая ускорения точки А направлена от точки к мгновенной оси (см. рисунок), а ее модуль равен

 .

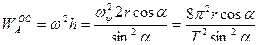Вращательная составляющая ускорения, равная

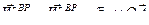 , расположена в плоскости рисунка и составляет угол 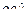c 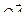 (см. рисунок). Ее модуль равен

 .

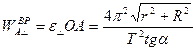Обе компоненты ускорения лежат в плоскости рисунка и составляют между собой угол ( 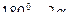). Тогда

 .

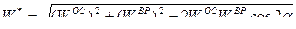Рассмотрим теперь более общий случай, когда вращение конического колеса вокруг вертикальной оси ускоренное (в этом случае полагаются известными величины угловой скорости 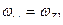 и углового ускорения  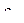вращательного движения вокруг вертикальной оси).

Если в рамках предыдущих исходных данных параллелограмм угловых скоростей равномерно вращался вокруг вертикальной оси без изменения размеров своих сторон, то в рассматриваемом случае, во-первых, вращение будет ускоренным, и, во-вторых, стороны будут возрастать, сохраняя при этом выведенные ранее соотношения. Так же остаются справедливыми формулы для расчета 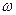, , ,  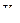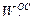и .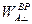

Продифференцировав формулу для расчета угловой скорости, получим:

 .

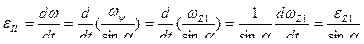Тогда вектор

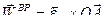перпендикулярен плоскости рисунка и направлен в противоположную от нас сторону, а его модуль .

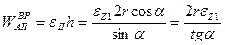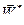Полное ускорение точки А будет результатом сложения двух ортогональных векторов  и 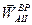, т.е.

.

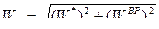Вопросы и задачи для самоконтроля

1. Дайте определение поступательного движения тела. Что можно сказать о траекториях, скоростях и ускорениях точек при таком движении тела?

2. Может ли быть окружность траекторией движения точек тела при поступательном движении? Каким будет движение подвесной кабины колеса обозрения?

3. Что можно сказать о глобальных и локальных кинематических характеристиках при поступательном движении тела?

4. Дайте определение вращательного движения тела. Сколько степеней свободы имеет тело в этом случае? Каковы его глобальные характеристики? Может ли ось вращения быть вне границ тела?

5. Как связаны величины локальных и глобальных кинематических характеристик при вращательном движении? Запишите формулы для величин скорости, осестремительной и вращательной составляющих ускорения точки, полного ускорения точки.

6. Как связаны векторы локальных и глобальных кинематических характеристик? Запишите формулы для векторов скорости, осестремительной и вращательной составляющих ускорения точки.

7. Что можно сказать о скоростях в точках контакта элементов, образующих простейшие механические передачи? 

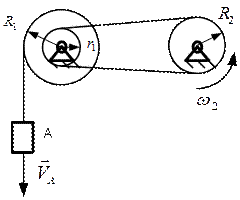
8. Найти угловую скорость  колеса 2, если известна скорость груза А и радиусы колес (нити полагать нерастяжимыми, проскальзывание – отсутствующим)?

Лекция 7