Примем в качестве независимых обобщенных координат, определяющих положение тела при плоскопараллельном движении (плоской фигуры при плоском движении), функции (51). Тогда глобальными кинематическими характеристиками движения будут так же скорость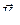 
и ускорение 
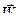полюса, угловая скорость 
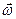и угловое ускорение 
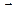вращения вокруг полюса.
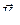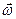Выражения для и получаются после дифференцирования функций (51):
;
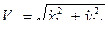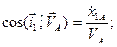
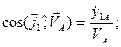(52)
,
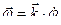где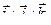 
- орты неподвижной координатной системы 
.
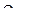Повторное дифференцирование позволяет определить 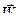и :
;
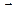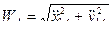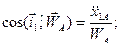
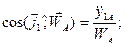(53)
.
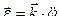В формулах (51)-(53) от выбора полюса зависят векторы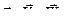 
7.3. Локальные кинематические характеристики и некоторые способы их определения
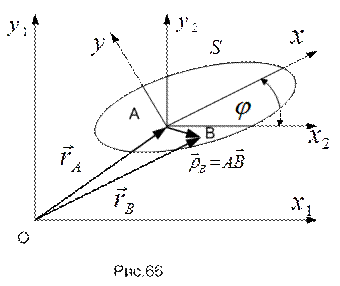
Пусть для плоской фигуры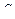 
известны уравнения движения (49). Найдем скорость и ускорение произвольной точки 
фигуры (рис.66).
Радиус-вектор 
, определяющий положение точки 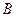в неподвижной системе отсчета, может быть представлен в виде
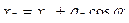
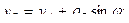(54)
где - радиус-вектор точки 
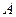в неподвижной системе отсчета, а 
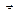- радиус-вектор точки 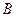в координатной системе 
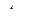(для недеформируемого тела 
).
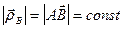Продифференцируем выражение (5.4) по времени:
.
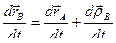Здесь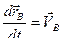 
и 
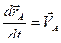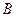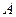- скорости точек и в неподвижной системе отсчета. Слагаемое
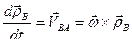(55)
есть скорость точки 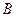в полусвязанной системе 
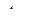, т.е. скорость, обусловленная вращением плоской фигуры вокруг полюса. Поэтому выражение для скорости точки 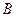примет вид
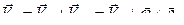, (56)
т.е. скорость произвольной точки 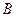плоской фигуры равна сумме скорости полюса 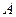и скорости точки 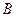при вращении плоской фигуры вокруг полюса .
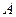Графическая интерпретация формулы (56) приведена на рис.67.
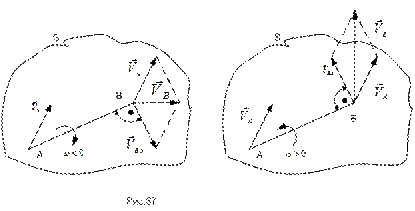
Модули и направления векторов, входящих в формулу (56), определяются из уравнений (52) и (55). При этом
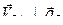. (57)
Для определения ускорения точки 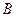продифференцируем равенство (56) по времени:
.
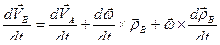Здесь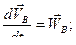 
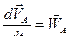- ускорения точек 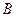и 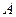в неподвижной системе отсчета; 
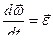- вектор углового ускорения; 
.
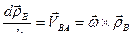Таким образом, ускорения точек 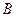и 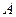связаны между собой соотношением
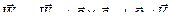. (58)
Второе и третье слагаемые являются соответственно вращательной (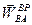 
) и осестремительной ( 
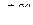) составляющими ускорения точки 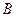при вращении плоской фигуры вокруг полюса ( 
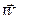) (см. рис.5.4.б). Тогда формулу (58) можно записать так
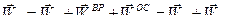. (59)
Графическая интерпретация формулы (59 при совпадающих по направлению векторах 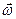и приводятся на рис.68.
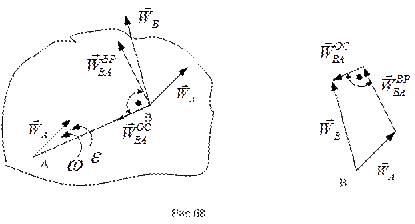
Ускорение 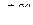направлено от рассматриваемой точки к полюсу, а ускорение 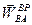- по перпендикуляру к отрезку АВ. Для определения модуля и направления ускорения точки 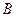следует воспользоваться уравнениями (53) и (58). При этом
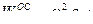
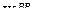. (60)
В некоторых случаях удобно использовать следующее полезное свойство: проекции скоростей точек твердого тела на прямую, проходящую через эти точки, равны между собой.
Для доказательства спроецируем (56) на прямую, проходящую через точк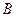и и 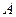. Очевидно, что проекция на эту прямую скорости 
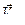равна нулю, т.к. 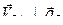. Тогда
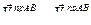. (61)
Отмеченное свойство справедливо и в общем случае движения твердого тела, так как является следствием неизменности расстояния АВ.
В том случае, когда за полюс выбрана точка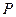 
, скорость которой равна нулю (рис.69), выражение (56) приобретает наиболее простой и удобный для расчета вид:
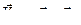. (62)
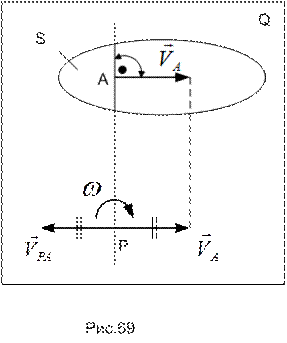
Это означает, что скорости точек при плоскопараллельном движении тела можно определять так же, как и в случае вращения тела вокруг неподвижной оси (см. пункт 6.2.2). При этом ось вращения движется; в каждый момент времени она перпендикулярна плоскости фигуры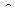 
и проходит через точку 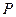. Она называется мгновенной осью вращения тела, а точка 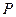- мгновенным центром скоростей (м.ц.с.) плоской фигуры. Часто мгновенная ось вращения – вне тела.
В некоторых случаях (рис.70) существование и положение такой точки очевидно. Так, если колесо катится без скольжения по рельсу, то равна нулю скорость той точки колеса, которая соприкасается с рельсом.
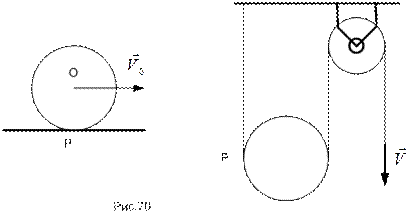
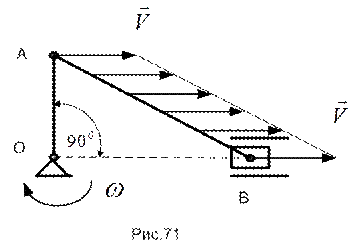
При плоском движении м.ц.с. существует всегда, за исключением случая, когда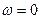 
и, значит, скорости всех точек тела равны и параллельны (рис.71).
Существует и иная трактовка, утверждающая, что м.ц.с. существует и в этом случае, но располагается в бесконечности.
Очевидно, что если при этом равны ускорения всех точек, то движение тела поступательное, плоское. При неравных ускорениях движение называется мгновенно-поступательным.
Так движутся точки шатуна АВ кривошипно-шатунного механизма (рис.71), обладая в рассматриваемом положении равными скоростями, но разными ускорениями.
При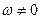 
возможны различные ситуации. В том случае, когда известны линии возможных направлений скоростей любых двух точек А и В плоской фигуры, м.ц.с. расположен на пересечении перпендикуляров к указанным линиям, восстановленным из этих точек (рис.72).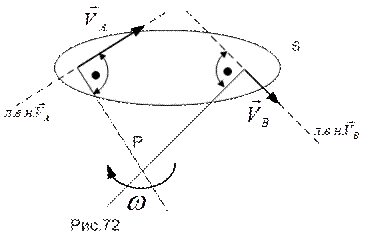 
Если перпендикуляры параллельны, то движение плоской фигуры мгновенно-поступательное либо поступательное, плоское. Если перпендикуляры совпадают, то для определения положения м.ц.с. необходимо знать дополнительно модули скоростей точек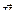 
и .
Тогда, используя формулу (62) и свойство пропорции, имеем:
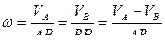. (63)
Соотношение (63) позволяет найти как длину любого из отрезков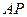 
или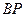 
, так и угловую скорость вращения тела.
ПРИМЕР 24. Судно на регулярном волнении совершает поперечную качку, причем угол крена судна изменяется по закону
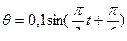, а центр тяжести судна G движется согласно уравнениям 
; 
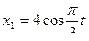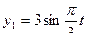. При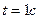 
определить скорость и ускорение вершины мачты А , которая расположена над центром тяжести судна на высоте 
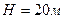(рис.73).
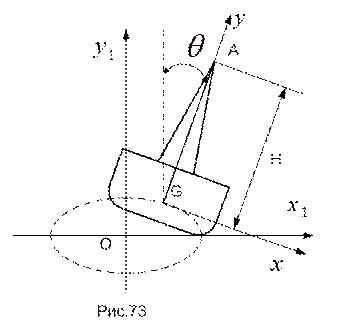
РЕШЕНИЕ. Примем за полюс центр тяжести судна – точку G. В момент времени 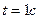координаты полюса и угол крена равны:
;
.
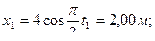
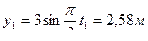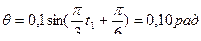Проекции скорости и ускорения полюса на оси неподвижной координатной системы при 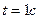имеют значения:
.
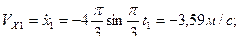
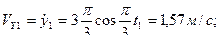
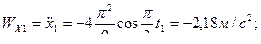
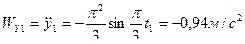Значение угловой скорости и ускорения при :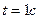
.
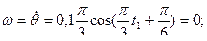
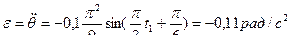Для скорости точки А можно записать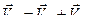 
.
Поскольку в рассматриваемый момент 
то 
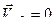и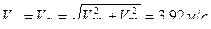 
.
Для ускорения точки А справедливо равенство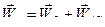 
.
На рис.74 показаны найденные выше составляющие ускорения полюса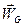 
, а так же вращательная составляющая ускорения 
:
( 
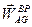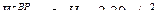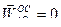так как ).
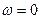Из рисунка следует:
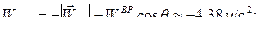
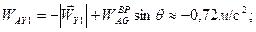
Отсюда получаем
.
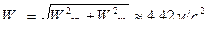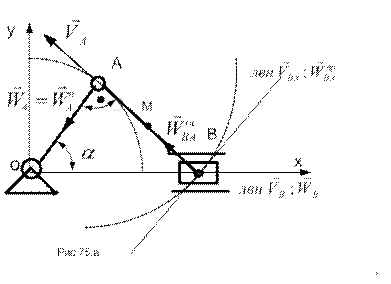
ПРИМЕР 25. Кривошип ОА кривошипно-шатунного механизма, изображенного на рисунке 75.а, вращается с заданной постоянной угловой скоростью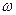 
. Длины кривошипа 
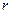и шатуна 
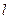известны. Для изображенного на рисунке положения механизма (заданы угол наклона кривошипа 
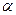и прямой угол между кривошипом и шатуном) найти скорости и ускорения точек А, В и М (точка М расположена на середине шатуна).
РЕШЕНИЕ. Сначала найдем скорость и ускорение точки А кривошипа, вращающегося с заданной угловой скоростью, как
.
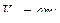
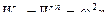Точка А является общей точкой кривошипа и шатуна, который совершает плоское движение. Для нахождения скорости и ускорения точки В воспользуемся методом полюса. Сначала построим треугольник скоростей (рис.75.б), соответствующий векторному равенству
.
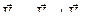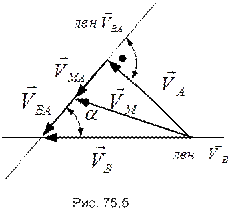
В этом треугольнике скорость точки А известна по величине и направлению, линия возможного направление (лвн) скорости точки В определена направляющими, а лвн скорости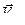 
должна быть перпендикулярна шатуну, так как траекторией точки В при вращении вокруг полюса является окружность радиуса АВ= 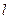. Из треугольника находим:
.
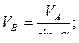
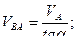
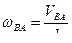Применим метод полюса для расчета скорости точки М.
.
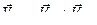Поскольку точка М делит шатун пополам,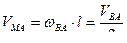 
. Треугольник для расчета скорости точки М построен внутри треугольника скоростей для точки В.
Очевидно, что аналогичные построения могут быть выполнены для любой точки шатуна. Совокупность таких построений для звена механизма называются его планом скоростей.
Для расчета ускорения точки В запишем формулу метода полюса:
.
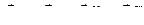В этом четырехугольнике (см. рис.75.в) ускорение полюса А определено ранее, ускорение 
следует вычислить и направить от точки В к точке А (см. рис.75.а), а направления ускорени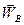й 
и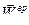 
совпадают с направлениями соответствующих скоростей.
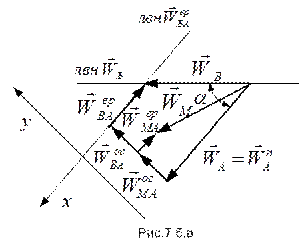
Спроецировав построенный векторный четырехугольник на выбранные координатные оси, получим два уравнения:
.
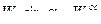Отсюда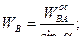 
.
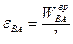Применим метод полюса для расчета ускорения точки М:
.
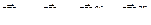Вычисленные величины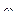 
и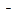 
позволяют найти соответствующие проекции ускорений. Четырехугольник ускорений для точки М построен внутри четырехугольника ускорений для точки В.
Очевидно, что аналогичные многоугольники могут теперь быть построены для любой точки шатуна. Совокупность таких построений для звена механизма носит название его плана ускорений.
ПРИМЕР 26. Колесо радиуса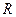 
катится без проскальзывания по горизонтальной поверхности. Скорость и ускорение центра А колеса заданы (см. рисунок 76.а). Определить скорость и ускорение точки В его горизонтального диаметра.
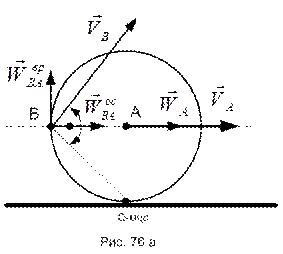
РЕШЕНИЕ. Точка О контакта колеса с неподвижной плоскостью является его мгновенным центром скоростей (мцс). В этом случае угловая скорость вращения колеса может быть найдена как
;
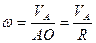а угловое ускорение как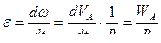 
.
Тогда скорость точки В будет перпендикулярна радиусу ВО до мцс, и равна
.
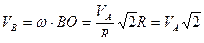Для определения ускорения точки В воспользуемся методом полюса
.
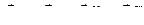Первое слагаемое в правой части известно, два других могут быть рассчитаны как
.
Четырехугольник ускорений приведен на рис. 76.б.
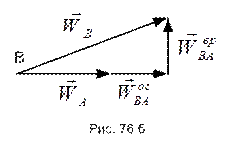
В рассматриваемом случае выражение для ускорения точки В будет
.
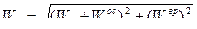Вопросы и задачи для самоконтроля
1. Дайте определение плоско – параллельного движения тела. Сколько степеней свободы, в общем случае, имеет при этом тело?
2. В чем суть метода полюса? Какие кинематические характеристики при таком движении являются глобальными? Что происходит с ними при смене полюса?
3. Запишите формулы для вычисления локальных кинематических характеристик по методу полюса.
4. Что такое «мгновенный центр скоростей» тела и как найти точку его расположения? Вычисление скоростей точек плоской фигуры при использовании этого понятия.
5. Теорема о проекциях скоростей точек плоской фигуры на линию, их соединяющую.
6. Найти скорость ползуна В плоского механизма в указанном положении, если скорость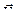 
ползуна А известна?
При решении сначала использовать методом полюса, потом найти мгновенный центр скоростей и воспользоваться им, затем использовать теорему о проекциях скоростей плоской фигуры. Сравнить трудоемкость получения результата различными приемами.
Лекция 8
Дата: 2019-03-05, просмотров: 349.
