Механическую передачу называют простейшей, если ее элементы двигаются поступательно либо вращаются вокруг неподвижной оси. На рис.57.а-в изображено несколько наиболее простых передач этого типа: барабан лебедки с поднимаемым грузом, рядовая зубчатая передача (ее колеса могут быть цилиндрическими либо коническими), цепная (либо ременная) передача.
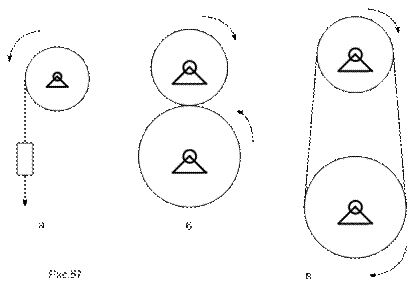
Суть кинематического расчета любой передачи состоит в том, что бы по известным кинематическим характеристикам элемента, (обычно называемого приводом), рассчитать кинематические характеристики остальных элементов передачи.
Соображение, на основании которого осуществляется переход от одного элемента к другому, достаточно очевидно: при отсутствии проскальзывания в точке контакта элементарные (бесконечно малые) линейные перемещения точек контактирующих элементов должны быть равны. Равенство элементарных линейных перемещений приводит к равенству скоростей и касательных составляющих ускорений соответствующих точек элементов.
ПРИМЕР 21. (задача 14.4 из [2]). В механизме стрелочного индикатора (см. рис.58) движение от рейки мерительного штифта 1 передается шестерне 2, на оси которой укреплено зубчатое колесо 3, сцепляющееся с шестерней 4, несущей стрелку. Определить угловую скорость стрелки, если движение штифта задано уравнением 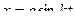 и радиусы зубчатых колес соответственно равны
и радиусы зубчатых колес соответственно равны 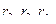
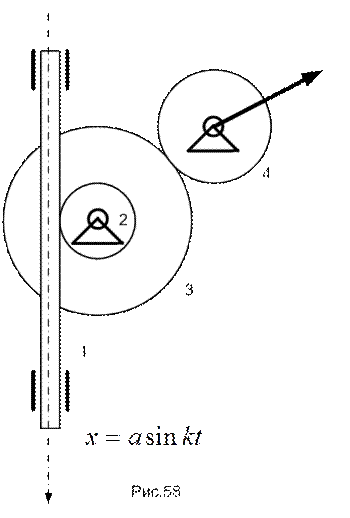
Проведем рассуждения, вычисляя скорости точек контактирующих элементов (как было сказано выше, можно было рассматривать элементарные линейные перемещения либо касательные ускорения).
Скорости точек поступательно двигающегося штифта одинаковы и равны  . В точке контакта точка А штифта и точка В шестерни 2 при отсутствии проскальзывания должны иметь равные скорости, т.е.
. В точке контакта точка А штифта и точка В шестерни 2 при отсутствии проскальзывания должны иметь равные скорости, т.е.
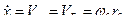 , где
, где 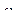 - угловая скорость вращения шестерни 2.
- угловая скорость вращения шестерни 2.
Шестерня 2 и зубчатое колесо 3 укреплены на общей оси вращения, следовательно, их угловые скорости одинаковы, т.е. 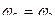 .
.
Скорости точек С и Д зубчатых колес 3 и 4 при так же должны быть равны между собой, тогда
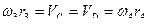 .
.
Поскольку стрелка индикатора прикреплена к шестерне 4, то их угловые скорости равны.
Записанные соотношения позволяют выразить через скорость штифта угловую скорость шестерни 2, затем угловую скорость шестерни 4, т.е. получить выражение
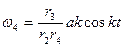 .
.
ПРИМЕР 22 (задача 14.2 из [2]). Редуктор скорости, служащий для замедления вращения и передающий вращение вала I валу II, состоит из четырех шестерен с соответствующим числом зубцов: 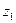 =10,
=10, 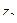 =60,
=60, 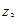 =12,
=12, 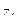 =70. Определить передаточное отношение механизма.
=70. Определить передаточное отношение механизма.
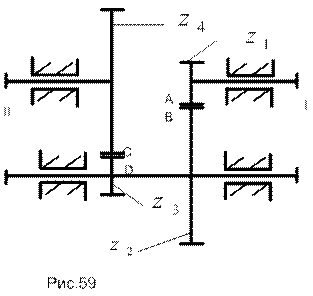
На рис.59 изобразим схему двухступенчатого редуктора; при этом шестерня 1, насаженная на вал I, находится в зацеплении с шестерней 2 (см. рис.57.б), насаженной на промежуточный вал, общий с шестерней 3, которая находятся в зацеплении с шестерней 4 (см. рис.57.б), последняя насажена на вал II.
Угловая скорость вала I есть угловая скорость шестерни 1. В силу отсутствия взаимного проскальзывания между шестернями 1 и 2 можно приравнять скорости в точке их контакта, т.е. 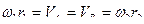 , где
, где 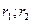 - радиусы соответствующих шестерен. Аналогичное выражение может быть записано для точки контакта шестерен 3 и 4, т.е.
- радиусы соответствующих шестерен. Аналогичное выражение может быть записано для точки контакта шестерен 3 и 4, т.е. 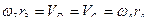 . Поскольку шестерни 2 и 3 насажены на общий промежуточный вал, их угловые скорости равны (
. Поскольку шестерни 2 и 3 насажены на общий промежуточный вал, их угловые скорости равны ( 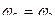 ). Полученные выражения позволяют получить отношение угловых скоростей валов I и II как
). Полученные выражения позволяют получить отношение угловых скоростей валов I и II как
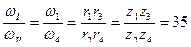 .
.
В окончательном выражении учтено, что число зубцов шестерни пропорционально ее радиусу (так как длина окружности шестерни, с одной стороны, равна произведению числа зубцов на длину одного зубца, а с другой, - произведению 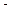 на радиус шестерни).
на радиус шестерни).
Дата: 2019-03-05, просмотров: 508.