Наиболее просто кинематические характеристики движения определяются в ортонормированном базисе 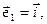
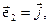
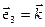 (единичные базисные векторы ортогональны). Обычно с этим базисом связывают декартову систему осей
(единичные базисные векторы ортогональны). Обычно с этим базисом связывают декартову систему осей 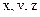 . Три числа
. Три числа 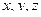 , которые определяют положение точки М относительно этой системы координат,- это проекции радиуса-вектора на координатные оси:
, которые определяют положение точки М относительно этой системы координат,- это проекции радиуса-вектора на координатные оси:

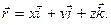 (25)
(25)
Координаты 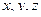 движущейся точки
движущейся точки

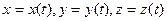 (26)
(26)
обычно полагают дважды дифференцируемыми по времени функциями. Сами уравнения (26) называют уравнениями движения точки в декартовой координатной системе или уравнениями траектории точки в параметрической форме. Если удается исключить из этих уравнений время 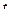 , то комбинации любых двух полученных соотношений
, то комбинации любых двух полученных соотношений 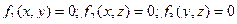 задают траекторию движения точки явно.
задают траекторию движения точки явно.
Для траектории движения, расположенной в одной плоскости (ее всегда можно совместить с плоскостью 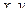 ), в (26) достаточно записать лишь первые два уравнения либо получить
), в (26) достаточно записать лишь первые два уравнения либо получить 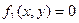 .
.
Продифференцировав (25) по времени, вектор скорости можно представить в форме:
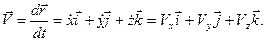 (27)
(27)
где 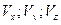 - проекции вектора скорости на соответствующие оси координат.
- проекции вектора скорости на соответствующие оси координат.
Модуль вектора скорости определяется по формуле
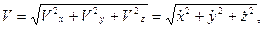 (28)
(28)
а направление этого вектора задается косинусами углов с соответствующими координатными осями («направляющие косинусы»):
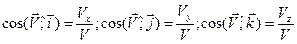 . (29)
. (29)
Выполнив такую же последовательность операций, можно получить выражения для вектора ускорения, его проекций, модуля и направляющих косинусов углов:
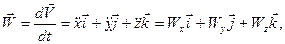
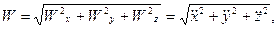 (30)
(30)
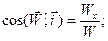
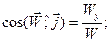
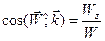 .
.
ПРИМЕР 13. Морское орудие, дульный срез которого расположен на высоте 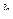 над уровнем моря, производит выстрел под углом
над уровнем моря, производит выстрел под углом 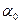 к горизонту; скорость вылета снаряда
к горизонту; скорость вылета снаряда 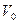 (см. рис.43).
(см. рис.43).
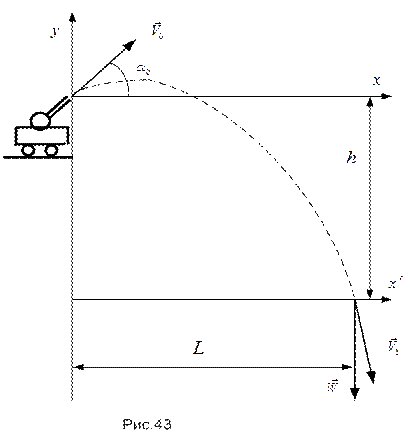
Полагая известными уравнения движения снаряда в декартовой координатной системе (начало координат на дульном срезе, 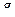 - ускорение свободного падения,
- ускорение свободного падения, 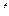 - время движения, сопротивление воздуха не учитывается):
- время движения, сопротивление воздуха не учитывается):
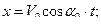
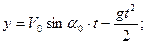
необходимо рассчитать дальность полета снаряда, его скорость и ускорение в момент удара о воду.
РЕШЕНИЕ. Формулы для вычисления проекций скорости и ускорения на оси декартовой системы получаются дифференцированием по времени уравнений движения снаряда:
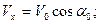
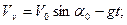
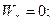
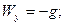
В общем случае значения величин проекций могут быть получены только после расчета времени полета снаряда  . Заметим, что в рассматриваемом случае на всем протяжении полета ускорение снаряда оказалось постоянным и равным ускорению свободного падения.
. Заметим, что в рассматриваемом случае на всем протяжении полета ускорение снаряда оказалось постоянным и равным ускорению свободного падения.
Время полета снаряда определим из условия 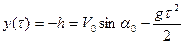 .
.
Решив квадратное уравнение относительно  , получим:
, получим:
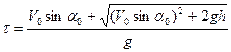 .
.
Второй, отрицательный, корень уравнения отброшен, как не имеющий физического смысла.
Подставим найденное значение в формулы для проекций скорости:
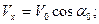
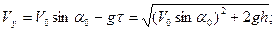
Тогда величина скорости снаряда при ударе о воду будет
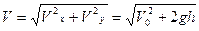 ,
,
а дальность полета снаряда равна
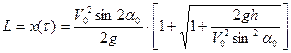 .
.
ПРИМЕР 14. Кривошип ОА кривошипно-шатунного механизма вращается с постоянной угловой скоростью 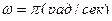 . В начальный момент времени кривошип занимал горизонтальное положение. Длина шатуна АВ = ОА = 80 см. Точка М шатуна лежит на его середине. Составить уравнения для вычисления координат точек А, В и М механизма в декартовой координатной системе, изображенной на рисунке 44. Найти положение точки М в момент времени
. В начальный момент времени кривошип занимал горизонтальное положение. Длина шатуна АВ = ОА = 80 см. Точка М шатуна лежит на его середине. Составить уравнения для вычисления координат точек А, В и М механизма в декартовой координатной системе, изображенной на рисунке 44. Найти положение точки М в момент времени 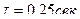 , а так же проекции скорости и ускорения, их модули и направляющие косинусы с координатными осями.
, а так же проекции скорости и ускорения, их модули и направляющие косинусы с координатными осями.
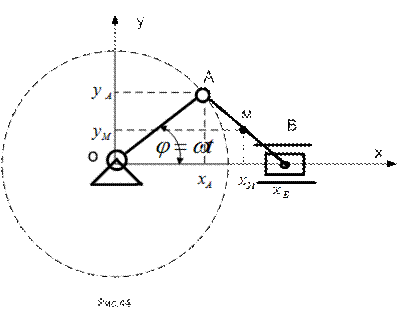
РЕШЕНИЕ. Запишем выражения для проекций точек механизма на оси декартовой координатной системы:
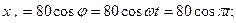
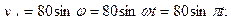
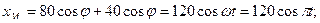
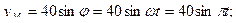
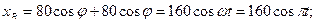
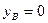 .
.
Для нахождения положения точки М в заданный момент времени подставим значение 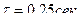 в выражения для проекций, тогда
в выражения для проекций, тогда
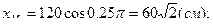
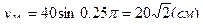 .
.
Для вычисления проекций скорости продифференцируем полученные выражения по времени и подставим величину 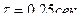 . Тогда
. Тогда
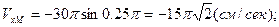
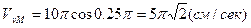 .
.
Теперь можно вычислить модуль вектора скорости и его направляющие косинусы:
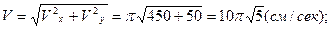
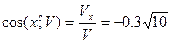 ;
; 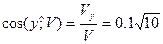 .
.
Для вычисления проекций ускорения второй раз продифференцируем полученные выражения по времени и подставим величину 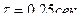 . Тогда
. Тогда
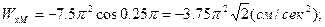
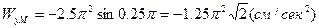 .
.
Теперь можно вычислить модуль вектора ускорения и его направляющие косинусы:
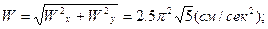
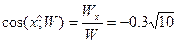 ;
; 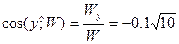 .
.
Результаты выполненных расчетов нанесены на рисунок 45.
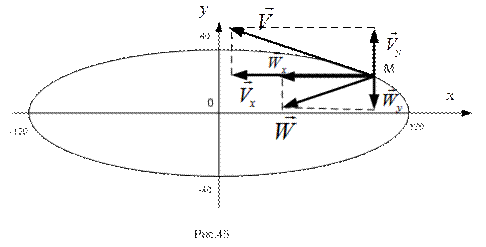
Дата: 2019-03-05, просмотров: 426.