Возьмем неподвижную координатную систему  и движущуюся по отношению к ней известным образом подвижную систему
и движущуюся по отношению к ней известным образом подвижную систему 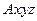 (см. рис. 78). Скорость точки М по отношению к системе
(см. рис. 78). Скорость точки М по отношению к системе  (абсолютная скорость) будем обозначать
(абсолютная скорость) будем обозначать 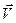 , скорость по отношению к системе
, скорость по отношению к системе 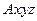 (относительная скорость) -
(относительная скорость) - 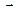 , скорость той точки подвижной системы, с которой в рассматриваемый момент времени совпадает точка М (переносная скорость) -
, скорость той точки подвижной системы, с которой в рассматриваемый момент времени совпадает точка М (переносная скорость) - 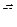 .
.
Продифференцируем равенство (64) по времени:
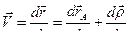 .
.
С учетом (66) и введенных обозначений, имеем
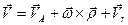 , (67)
, (67)
где 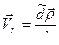 .
.
Первые два слагаемых в формуле (67) являются скоростью точки подвижной координатной системы, совпадающей с точкой М в данный момент времени, т.е. являются ее переносной скоростью 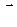 . В таком случае абсолютная скорость точки равна сумме ее переносной и относительной скоростей.
. В таком случае абсолютная скорость точки равна сумме ее переносной и относительной скоростей.
Окончательный вид формулы (67) будет
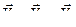 . (68)
. (68)
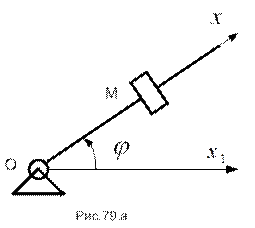
ПРИМЕР 27 (задача 23.31 из [2]). Шайба М движется по горизонтальному стержню ОА так, что  . В то же время стержень вращается вокруг горизонтальной оси, проходящей через точку О, по закону
. В то же время стержень вращается вокруг горизонтальной оси, проходящей через точку О, по закону 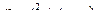 (см. рис.79.а). Определить радиальную и трансверсальную составляющие абсолютной скорости и ускорения шайбы в момент времени
(см. рис.79.а). Определить радиальную и трансверсальную составляющие абсолютной скорости и ускорения шайбы в момент времени 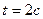 .
.
РЕШЕНИЕ. Примем за относительное движение шайбы ее движение вдоль стержня ОА по закону  ; картина этого движения (КОД) и радиальная составляющая скорости шайбы (скорость в относительном движении), вычисленная для момента времени
; картина этого движения (КОД) и радиальная составляющая скорости шайбы (скорость в относительном движении), вычисленная для момента времени 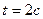 , изображена на рис.79.б.
, изображена на рис.79.б.
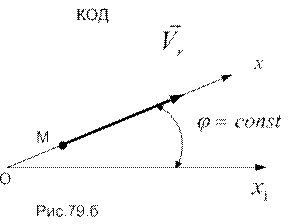
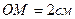 ;
; 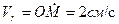 .
.
Переносным движением шайбы М будет движение точки стержня, находящейся в рассматриваемый момент времени под шайбой. Для расчета ее скорости сначала необходимо рассчитать угловую скорость и угловое ускорение стержня ОА:
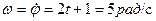 ;
; 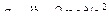 ;
;
 .
.
Картина переносного движения (КПД) и вычисленная для заданного момента времени трансверсальная составляющая скорости (скорость шайбы в переносном движении) изображены на рис.79.в.
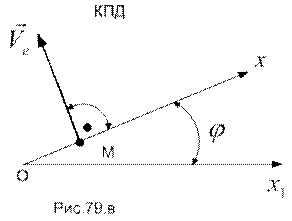
При необходимости можно найти величину абсолютной скорости шайбы как геометрическую сумму ее составляющих. В данном случае
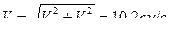 .
.
Вычисление соответствующих проекций ускорения шайбы будет выполнено ниже в ПРИМЕРЕ 29.
ПРИМЕР 28 (задача 22.3 из [2]). Корабль, проходящий точку А, движется с постоянной по модулю и направлению скоростью  . Под каким углом
. Под каким углом 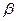 к прямой АВ надо начать двигаться катеру из точки В, чтобы встретиться с кораблем, если скорость катера постоянна по модулю и направлению и равна
к прямой АВ надо начать двигаться катеру из точки В, чтобы встретиться с кораблем, если скорость катера постоянна по модулю и направлению и равна 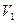 ? Линия АВ составляет угол
? Линия АВ составляет угол  с перпендикуляром к курсу корабля.
с перпендикуляром к курсу корабля.
РЕШЕНИЕ. На рис.80 схематично изображена акватория, где движутся точки А (корабль) и В (катер). Точкой С обозначено место их предполагаемой встречи.
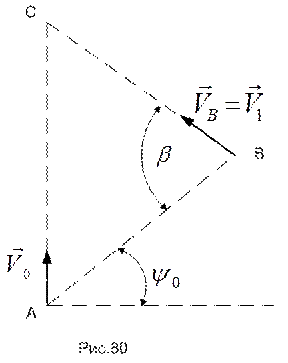
Представим прямолинейное движение катера (по прямой BС) как сложное, состоящее из переносного движения вместе с кораблем (поступательное движение по прямой АС) и относительного – по отношению к кораблю (в момент старта катера - движение по прямой АВ). Тогда
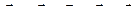 .
.
В этом треугольнике известны модули скоростей корабля  и катера
и катера 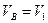 , а так же угол
, а так же угол  между скоростью корабля и линией АВ. Теорема синусов позволяет записать соотношение
между скоростью корабля и линией АВ. Теорема синусов позволяет записать соотношение
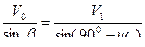 .
.
Тогда 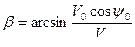 .
.
Дата: 2019-03-05, просмотров: 440.