Задание положения точки. Естественный трехгранник кривой и его оси
В технических приложениях выделяется круг задач о движении точки по заранее известной траектории (в общем – криволинейной). В таких случаях для описания движения точки достаточно задаться лишь одной криволинейной координатой – длиной дуги 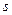 , измеряемой вдоль траектории от избранного на траектории начала
, измеряемой вдоль траектории от избранного на траектории начала 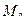 (рис.46).
(рис.46).

Движение точки 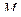 определится законом изменения дуги как функции времени
определится законом изменения дуги как функции времени
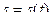 . (31)
. (31)
Дуговая координата 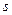 точки, в общем случае, отличается от пройденного пути, который является неубывающей функцией времени (они совпадают при условии движения точки по траектории только в одну сторону).
точки, в общем случае, отличается от пройденного пути, который является неубывающей функцией времени (они совпадают при условии движения точки по траектории только в одну сторону).
Для определения скорости и ускорения несвободной точки напомним некоторые сведения из дифференциальной геометрии пространственных кривых.
Плоскость  , перпендикулярная касательной
, перпендикулярная касательной  к траектории в точке
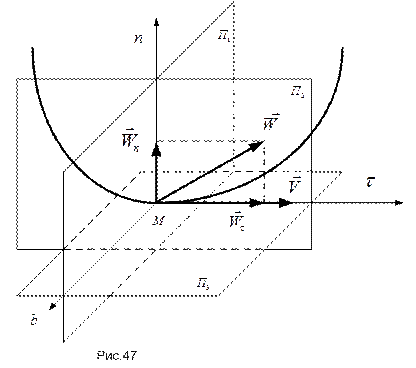
к траектории в точке  , называется нормальной плоскостью (рис.47). Любая прямая, лежащая в этой плоскости и проходящая через точку
, называется нормальной плоскостью (рис.47). Любая прямая, лежащая в этой плоскости и проходящая через точку 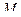 , направлена по нормали к кривой.
, направлена по нормали к кривой.
Касательную к траектории в точке 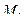 , близко расположенной к точке
, близко расположенной к точке 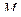 , обозначим
, обозначим 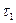 , а дугу
, а дугу 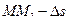 (см. рис.46).
(см. рис.46).
Если перенести прямую 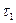 параллельно самой себе в точку
параллельно самой себе в точку 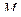 , то можно провести плоскость, содержащую прямые
, то можно провести плоскость, содержащую прямые  и
и 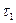 ; угол
; угол 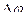 между этими прямыми называется углом смежности. С уменьшением
между этими прямыми называется углом смежности. С уменьшением 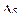 до нуля эта плоскость, поворачиваясь вокруг прямой
до нуля эта плоскость, поворачиваясь вокруг прямой  , приближается к некоторому предельному положению – соприкасающейся плоскости
, приближается к некоторому предельному положению – соприкасающейся плоскости 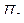 (см. рис.46). Прямая, по которой пересекаются нормальная и соприкасающаяся плоскости, называется главной нормалью к кривой в точке
(см. рис.46). Прямая, по которой пересекаются нормальная и соприкасающаяся плоскости, называется главной нормалью к кривой в точке 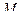 . Нормаль, перпендикулярная главной нормали, называется бинормалью кривой. Плоскость
. Нормаль, перпендикулярная главной нормали, называется бинормалью кривой. Плоскость 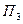 , проходящая через касательную и бинормаль в точке М, называется спрямляющей плоскостью.
, проходящая через касательную и бинормаль в точке М, называется спрямляющей плоскостью.
Нормальная, соприкасающаяся и спрямляющая плоскости образуют естественный трехгранник кривой в точке 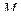 , а оси
, а оси 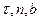 являются его осями. Единичные орты этих осей образуют ортонормированный базис локальной естественной координатной системы.
являются его осями. Единичные орты этих осей образуют ортонормированный базис локальной естественной координатной системы.
Скорость и ускорение точки
Найдем проекции векторов скорости 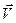 и ускорения
и ускорения 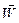 точки в естественном базисе.
точки в естественном базисе.
Радиус-вектор точки 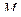 представляет собой сложную функцию времени
представляет собой сложную функцию времени 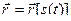 , поэтому
, поэтому
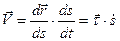 . (32)
. (32)
При выводе формулы учтено, что
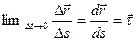 - является единичным ортом касательной к траектории движения точки
- является единичным ортом касательной к траектории движения точки 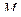 .
.
По определению ускорения имеем
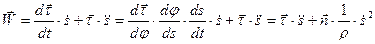 . (33)
. (33)
При выводе формулы учтено, что, во-первых,
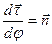 - есть орт главной нормали, а, во-вторых, кривизна траектории
- есть орт главной нормали, а, во-вторых, кривизна траектории 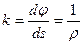 , где
, где 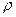 - радиус кривизны траектории в точке
- радиус кривизны траектории в точке 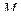 .
.
Для доказательства первого обстоятельства продифференцируем по углу смежности скалярное произведение
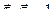 . Получим, что
. Получим, что 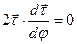 , т.е. скалярное произведение двух векторов, расположенных в соприкасающейся плоскости, равно нулю. Это возможно только в случае их ортогональности.
, т.е. скалярное произведение двух векторов, расположенных в соприкасающейся плоскости, равно нулю. Это возможно только в случае их ортогональности.
Величина проекции ускорения на касательную
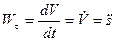 называется касательным ускорением, оно характеризует изменение вектора скорости по величине. Величина проекции ускорения на главную нормаль
называется касательным ускорением, оно характеризует изменение вектора скорости по величине. Величина проекции ускорения на главную нормаль
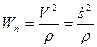 называется нормальным ускорением, оно характеризует изменение вектора скорости по направлению. Нормальное ускорение всегда направлено к центру кривизны траектории.
называется нормальным ускорением, оно характеризует изменение вектора скорости по направлению. Нормальное ускорение всегда направлено к центру кривизны траектории.
Полное ускорение точки 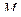 равно
равно
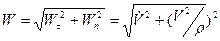 .
.
Заметим, что в выбранной координатной системе отсутствуют проекции скорости на главную нормаль и бинормаль, а так же проекция на бинормаль ускорения точки.
Рассмотрим несколько частных случаев движения точки.
1.Равномерное движение точки по прямой. Скорость движения не изменяется, поэтому равно нулю касательное ускорение.
Нормальное ускорение так же равно нулю (бесконечно большой радиус кривизны). Тогда
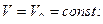
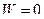 .
.
2.Равнопеременное движение по прямой ( 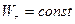 ). Нормальное ускорение равно нулю. Тогда
). Нормальное ускорение равно нулю. Тогда
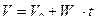 ;
; 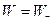 .
.
3. Равномерное движение по окружности радиуса 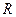 . Вектор скорости направлен по касательной к окружности (к радиусу - под прямым углом). Скорость движения не изменяется по величине, поэтому равно нулю касательное ускорение. Полное ускорение равно нормальному, т.е.
. Вектор скорости направлен по касательной к окружности (к радиусу - под прямым углом). Скорость движения не изменяется по величине, поэтому равно нулю касательное ускорение. Полное ускорение равно нормальному, т.е. 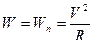 . Ускорение
. Ускорение  направлено к центру окружности.
направлено к центру окружности.
4. Равнопеременное движение по окружности радиуса 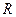 . В этом случае скорость изменяется и по величине и по направлению, поэтому
. В этом случае скорость изменяется и по величине и по направлению, поэтому
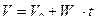 ;
; 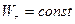 ;
; 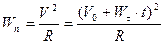 ;
; 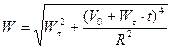 .
.
ПРИМЕР 15. Центр тяжести катера, разгоняющегося из состояния покоя, описывает дугу окружности радиуса R=75м. Его касательное ускорение изменяется по закону 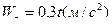 . Определить скорость и ускорение центра тяжести катера в момент, когда он пройдет путь 50 м.
. Определить скорость и ускорение центра тяжести катера в момент, когда он пройдет путь 50 м.
РЕШЕНИЕ. Интегрируя условие 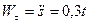 дважды по времени с учетом нулевых начальных условий, получим:
дважды по времени с учетом нулевых начальных условий, получим:
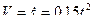 ;
; 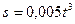 .
.
Значение 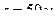 достигается в момент времени
достигается в момент времени 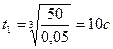 . При этом скорость центра тяжести катера будет
. При этом скорость центра тяжести катера будет 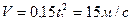 , а касательное ускорение -
, а касательное ускорение - 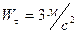 . Тогда полное ускорение равно
. Тогда полное ускорение равно
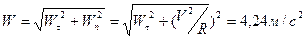 .
.
5.4. Связь кинематических характеристик при различных способах задания положения точки
В качестве примера разберем переход от задания положения точки в декартовой координатной системе к ее заданию в естественной координатной системе, а так же выведем формулы связи между соответствующими кинематическими характеристиками.
Пусть заданы уравнения движения точки в декартовой координатной системе 
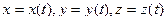 . Как уже говорилось выше, будем полагать эти функции дважды дифференцируемыми по времени.
. Как уже говорилось выше, будем полагать эти функции дважды дифференцируемыми по времени.
Записанные уравнения могут быть трактованы как уравнения траектории точки в параметрической форме. Если удается исключить из этих уравнений время 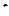 , то комбинации любых двух полученных соотношений
, то комбинации любых двух полученных соотношений 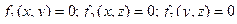 задают траекторию движения точки явно как линию пересечения соответствующих поверхностей.
задают траекторию движения точки явно как линию пересечения соответствующих поверхностей.
Для траектории движения, расположенной в одной плоскости (ее всегда можно совместить с плоскостью 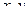 ), достаточно записать первые два уравнения либо получить
), достаточно записать первые два уравнения либо получить 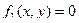 .
.
Координаты точки начала движения получаются подстановкой начального времени (обычно 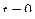 ) в уравнения движения, а анализ изменения координат с ростом параметра
) в уравнения движения, а анализ изменения координат с ростом параметра  определяет положительность или отрицательность направления движения вдоль траектории.
определяет положительность или отрицательность направления движения вдоль траектории.
Теперь получим зависимость криволинейной координаты от времени. Для этого воспользуемся формулами для вычисления скорости точки в декартовой и естественной координатных системах:
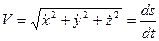 (34)
(34)
Разделим переменные и возьмем интегралы от правой и левой частей равенства. Получим
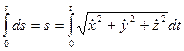 (35)
(35)
ПРИМЕР 16. По заданным уравнениям движения точки на плоскости
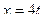 ;
; 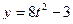
найти ее траекторию, указать начало движения, его положительное направление, а так же получить закон изменения во времени криволинейной координаты точки.
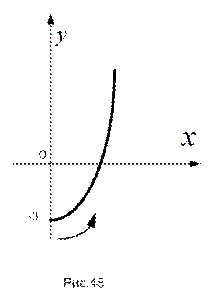
РЕШЕНИЕ. Исключим время из уравнений движения точки, выразив время 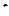 из первого уравнения и подставив его во второе уравнение. Получим уравнение параболы
из первого уравнения и подставив его во второе уравнение. Получим уравнение параболы 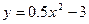 . Так как время не может быть отрицательным (
. Так как время не может быть отрицательным ( 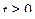 ), траектория точки – правая ветвь параболы (см. рис.48).
), траектория точки – правая ветвь параболы (см. рис.48).
Подставив 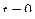 в уравнения движения, получим координаты точки начала движения:
в уравнения движения, получим координаты точки начала движения:
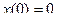 ;
; 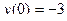 .
.
Анализ изменения координат при возрастании времени показывает, что и абсцисса и ордината точки возрастают; что соответствует движению точки от начального положения вправо вверх (на рисунке положительное направление движения указано стрелкой).
Для получения закона изменения криволинейной координаты от времени сначала найдем выражения для соответствующих проекций скорости 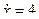 ;
; 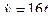 , а затем воспользуемся соотношением (2.4). Тогда
, а затем воспользуемся соотношением (2.4). Тогда
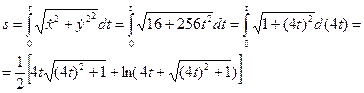 .
.
ПРИМЕР 17. По заданным уравнениям движения точки на плоскости
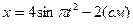 ;
; 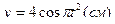
найти ее траекторию, указать начало движения и его положительное направление, а так же записать закон изменения во времени криволинейной координаты точки.
РЕШЕНИЕ. Для исключения времени из уравнений движения воспользуемся известным тригонометрическим соотношением 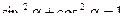 . В этом случае уравнение траектории будет иметь вид
. В этом случае уравнение траектории будет иметь вид 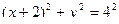 (окружность радиуса 4 см, сдвинутая на 2 см вдоль оси абсцисс влево, изображена на рис.49).
(окружность радиуса 4 см, сдвинутая на 2 см вдоль оси абсцисс влево, изображена на рис.49).
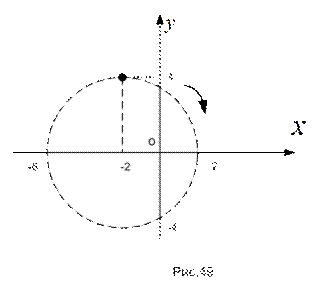
Подставив 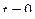 в уравнения движения, получим координаты точки начала движения:
в уравнения движения, получим координаты точки начала движения:
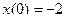 ;
; 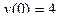 .
.
Анализ изменения координат при возрастании времени показывает, что абсцисса точки возрастает, а ордината убывает; что соответствует движению точки от начального положения вправо вниз (на рисунке положительное направление движения указано стрелкой).
Для получения закона изменения криволинейной координаты от времени сначала найдем выражения для соответствующих проекций скорости 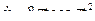 ;
; 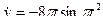 , а затем воспользуемся соотношением (6.4). Тогда
, а затем воспользуемся соотношением (6.4). Тогда
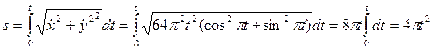 .
.
Формула (2.4) показывает связь между вычислением скорости точки в декартовой и естественной координатных системах
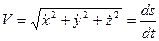 .
.
Для получения связи между вычислением ускорения точки в указанных координатных системах запишем формулы для его касательной и нормальной составляющих ускорения через проекции скорости и ускорения на оси декартовой координатной системы:
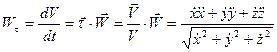 (36)
(36)
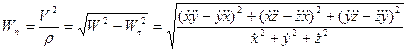
(37)
Радиус кривизны траектории в рассматриваемой точке может быть вычислен как
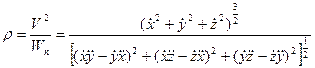 (38)
(38)
ПРИМЕР 18. Продолжить решение предыдущего примера, определив положение точки М и вычислив в декартовой и естественной координатных системах ее скорость и ускорение в момент времени 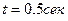 .
.
РЕШЕНИЕ. Для определения положения точки М подставим 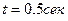 в уравнения движения точки:
в уравнения движения точки:
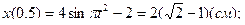 ;
; 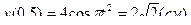 .
.
Теперь вычислим проекции скорости и ускорения точки М в декартовой координатной системе, взяв соответствующие производные по времени от уравнений движения точки и подставив в них время 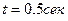 . Тогда получим:
. Тогда получим:
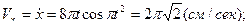
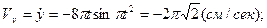
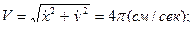
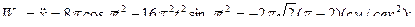
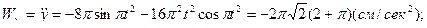
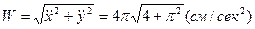 .
.
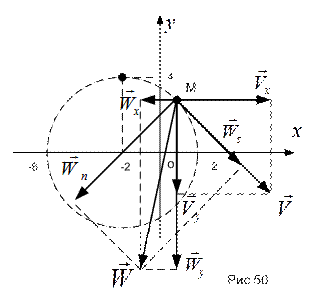
Все вычисленные характеристики нанесены на рис.50.
Для определения положения точки М на окружности подставим 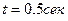 в закон изменения криволинейной координаты:
в закон изменения криволинейной координаты:
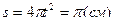 .
.
Поскольку длина окружности радиуса 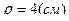 будет
будет 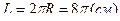 , то точка М за указанное время прошла в положительном направлении одну восьмую часть окружности.
, то точка М за указанное время прошла в положительном направлении одну восьмую часть окружности.
Теперь вычислим скорость и проекции ускорения точки на оси естественной координатной системы, взяв соответствующие производные от полученного выше закона изменения криволинейной координаты 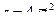 :
:
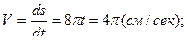
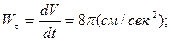
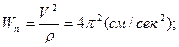
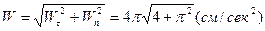 .
.
При желании можно убедиться, что вычисления по формулам (36, 37 и 38) совпадают с полученными результатами.
Все вычисленные кинематические характеристики так же нанесены на рис.50.
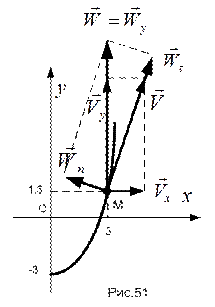
ПРИМЕР 19. Продолжить решение примера 16, определив положение точки М и вычислив в декартовой и естественной координатных системах ее скорость и ускорение в момент времени 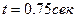 .
.
РЕШЕНИЕ. Для определения положения точки М в декартовой координатной системе подставим 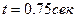 в уравнения движения точки:
в уравнения движения точки:
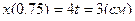 ;
; 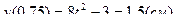 .
.
Теперь вычислим проекции скорости и ускорения точки М, взяв соответствующие производные по времени от уравнений движения точки и подставив в них время 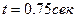 . Тогда получим:
. Тогда получим:
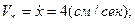
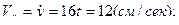
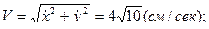
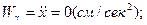
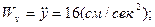
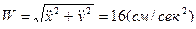 .
.
Для вычисления касательной и нормальной проекций ускорения и радиуса кривизны траектории в точке М воспользуемся формулами (36, 37 и 38). В случае движения точки по плоскости формулы примут более простой вид:
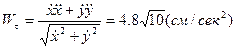 ;
;
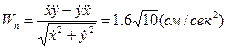 ;
;
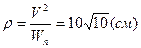 .
.
Все вычисленные характеристики нанесены на рис.51.
Вопросы и задачи для самоконтроля
1. Запишите формулы для скорости и ускорения точки при векторном способе задания ее положения. Каковы достоинства и недостатки этого способа?
2. В каком случае величины средней скорости точки и скорости в данный момент времени совпадают?
3. Запишите формулы для проекций скорости и ускорения точки при задании ее положения в декартовой системе координат.
4. Вычислите величину скорости точки через 1 секунду после начала движения, если ее положение на плоскости  задано радиусом – вектором
задано радиусом – вектором 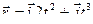 , где
, где  - орты координатных осей. Размерность проекций радиуса – вектора - метр, времени – секунда.
- орты координатных осей. Размерность проекций радиуса – вектора - метр, времени – секунда.
5. Что должно быть известно при естественном способе задания положения точки?
6. Что характеризует нормальная составляющая ускорения? Запишите формулу для ее вычисления. Как направлена эта составляющая по отношению к траектории?
7. Что характеризует касательная составляющая ускорения? Запишите формулу для ее вычисления.
8. Как движется точка по траектории, если скорость и касательная составляющая ускорения сонаправлены? Если они направлены в разные стороны?
9. Чему равна проекция ускорения точки на бинормаль?
10. По какой траектории движется точка, если векторы ее скорости и ускорения сонаправлены?
Лекция 6:
Дата: 2019-03-05, просмотров: 542.