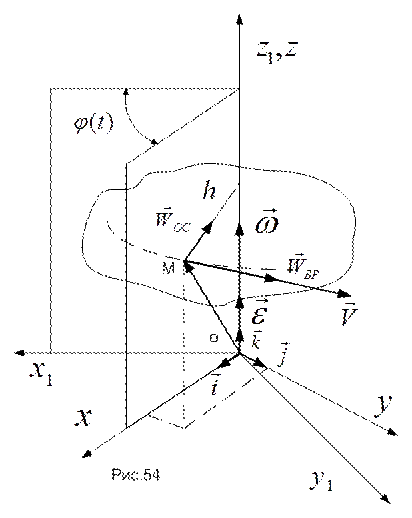
Для определения скорости и ускорения точки (локальные кинематические характеристики) тела, вращающегося вокруг неподвижной оси, могут быть использованы формулы (32) и (33), полученные при рассмотрении естественного способа задания положения точки. В частном случае – при движении точки по окружности постоянного радиуса 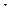 (см. рис. 54), элемент длины дуги окружности будет
(см. рис. 54), элемент длины дуги окружности будет 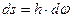 . Тогда:
. Тогда:
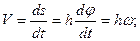
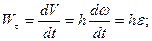
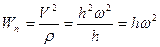 . (43)
. (43)
Заметим, что полученное для скорости выражение может быть представлено как результат векторного произведения
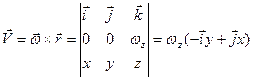 . (44.а)
. (44.а)
Оба выражения для скорости точки M дают один и тот же результат, так как при вращении вокруг неподвижной оси z 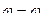 .
.
Окончательно для проекций вектора скорости точки М на оси подвижной координатной системы и его величины имеем:
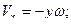
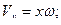
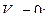
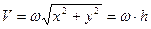 . (44.б)
. (44.б)
Заметим, что вычисление модуля векторного произведения дает тот же результат:
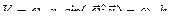 . (44.в)
. (44.в)
Для получения ускорения точки М продифференцируем по времени выражение (44.а):
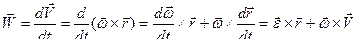 . (45)
. (45)
Первое слагаемое в (45) называют вращательным ускорением, а второе – осестремительным. Модули этих составляющих и модуль ускорения точки определяются выражениями
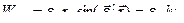
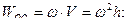
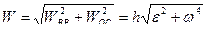 . (46)
. (46)
Если рассматривать движение точки по окружности, то первая составляющая является касательной составляющей ускорения, а вторая – нормальной (сравните выражения (43) и (46)).
На рис.54 изображены скорость и составляющие ускорения точки М при ускоренном вращении тела.
Необходимо отметить, что использование векторных соотношений особенно удобно при выполнении расчетов на ЭВМ, при этом векторы представляются в виде матриц, операции с которыми для ЭВМ являются стандартными.
ПРИМЕР 20. Антенна радиолокатора, шарнирно укрепленная на мачте судна, начинает вращаться в горизонтальной плоскости (вид сверху изображен на рис.55).
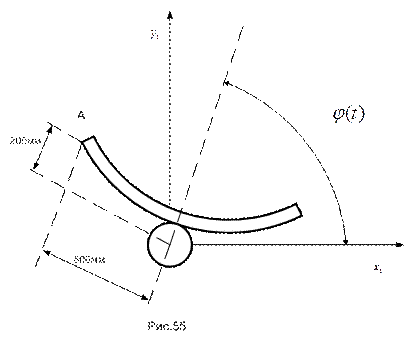
При этом угол между осью луча антенны и диаметральной плоскостью судна нарастает по закону 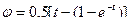 . Найти угловую скорость и угловое ускорение антенны, а так же скорость и ускорение ее точки А для трех моментов времени:
. Найти угловую скорость и угловое ускорение антенны, а так же скорость и ускорение ее точки А для трех моментов времени: 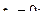
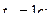
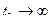 . Линейные размеры антенны указаны на рисунке.
. Линейные размеры антенны указаны на рисунке.
РЕШЕНИЕ. Получим выражения для глобальных кинематических характеристик антенны:
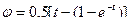 ;
;
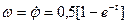 ;
;
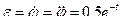 .
.
Мгновенные значения этих величин для трех моментов времени сведем в таблицу 3.1.
В формулах (3.6) и (3.8) для определения скоростей и ускорений точки А, а так же ее осестремительной и вращательной составляющих, расстояние от точки А до оси вращения будет 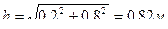
Результаты вычислений так же занесем в таблицу.
| 0 | 1 | 
|
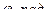
| 0 | 0,18 | 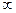
|
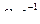
| 0 | 0,32 | 0,50 |
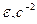
| 0,50 | 0/18 | 0 |
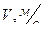
| 0 | 0,26 | 041 |
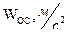
| 0 | 0,08 | 0,20 |
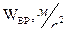
| 0,41 | 0,15 | 0 |
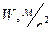
| 0,41 | 0,17 | 0,20 |
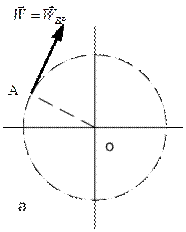
Из полученных данных следует, что антенна начинает разгоняться с довольно большим угловым ускорением, которое впоследствии уменьшается. Вскоре (хотя формально при 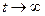 ) антенна выходит на режим установившегося вращения. Начальное ускорение точки А состоит только из вращательной составляющей (рис.56.а).
) антенна выходит на режим установившегося вращения. Начальное ускорение точки А состоит только из вращательной составляющей (рис.56.а).
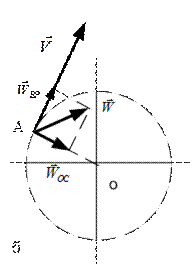
Скорость и ускорение точки А, а так же его составляющие, имеющие место на этапе разгона (  ), изображены на рис.56.б.
), изображены на рис.56.б.
Скорость и ускорение на заключительном этапе движения изображены на рис.56.в.
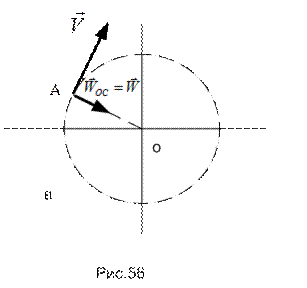
Дата: 2019-03-05, просмотров: 500.