Ковариационный анализ
Ковариационный анализ анализирует зависимость среднего значения некоторой СВ Y одновременно от набора количественных показателей (факторов) X и качественных F (индикаторных, неколичественных).
По отношению к Y переменные Х называются сопутствующими, а факторы F задают сочетание условий качественной природы, при которых полученные наблюдения Y и Х описываются с помощью, так называемых, индикаторных переменных.
Среди сопутствующих и индикаторных переменных могут быть как случайные, так и неслучайные (контролируемые в эксперименте).
Если СВ Y является вектором, то говорят о многомерном ковариационном анализе.
Часто рассматриваются линейные модели ковариационного анализа:
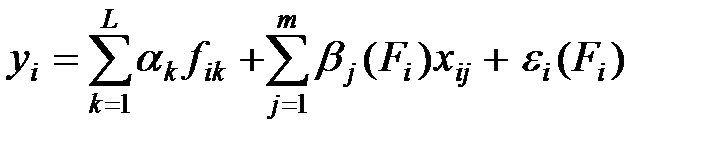 ,
,
где i = 1, 2, ..., n – индекс наблюдения;
k = 1, 2, ..., L – индекс типа условий эксперимента;
j = 1, 2, ..., m – индекс сопутствующей переменной;
fik – индикаторные переменные: fik = 1, если k – е уравнение имело место при yi, fik = 0, в ином случае;
a k – коэффициент влияния k – го условия;
xij – значение сопутствующей переменной Xj, при которой получено наблюдение yi, (i = 1, 2, ..., n; j = 1, 2, ..., m);
b j(Fi) – коэффициенты регрессии Y по Xj, зависящие от конкретного сочетания условий эксперимента, т.е. от вектора Fi = (fi1, fi2,..., fiL)T;
e i(Fi) – случайные ошибки, имеющие нулевые средние значения.
Основное содержание ковариационного анализа заключается в построении статистических оценок для неизвестных параметров a k, (k = 1, 2, m..., L) и b j (j = 1, 2, ..., m) и статистических критериев для проверки различных гипотез относительно значений этих параметров.
Если в рассматриваемой модели постулировать априори b1 = b2 =…= b m = 0, то получится модель дисперсионного анализа.
Если исключить влияние неколичественных факторов (положить a1 = a2 = = a L = 0), то получится модель регрессионного анализа.
Своим названием ковариационный анализ обязан тому, что в его вычислениях используются разбиения величин Y по X точно так же, как в дисперсионном анализе используются разбиения суммы квадратов отклонений Y.
Конфлюэнтный анализ
Конфлюэнтный анализ – совокупность методов математической статистики, относящихся к анализу априори постулируемых функциональных связей между количественными (случайными и неслучайными) переменными Х1, Х2, ..., Хm, в условиях, когда наблюдаются не сами переменные Хj, (j = 1, 2, ..., m), а случайные величины
х*ij, = хij, + e i; i = 1, 2, ... n,
где e i –случайная ошибка измерения хij переменной Хj, в i–м наблюдении.
При этом общий вид исследуемых функциональных (структурных) соотношений между ненаблюдаемыми переменными считается заданным.
В задачу конфлюэнтного анализа входит построение статистических значений для неизвестных значений параметров, участвующих в уравнениях исследуемых структурных отношений, а также статистических критериев, предназначенных для проверки различных гипотез о природе анализируемых связей.
В рамках линейной модели (или линеаризованному с помощью подходящих преобразований исходных переменных) априорное постулирование m линейных связей между Q (Q < m) переменными может быть сформулировано как допущение существования к – m общих факторов, таких что
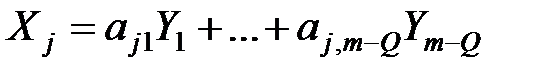 ,
,
причём матрица 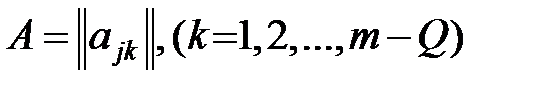 имеет ранг m – Q.
имеет ранг m – Q.
Параметризация модели конфлюэнтного анализа в рассматриваемом виде позволяет сформулировать основные задачи в терминах статистического оценивая неизвестных значений параметров аjк и статистической проверки гипотез, с ними связанных.
Формально модель выглядит также, как модель факторного анализа, однако задачи этих методов почти не пересекаются.
Если цель конфлюэнтного анализа – описание структурных соотношений, существующих между переменными Х1, Х2, ..., Хm, то в факторном анализе основной задачей является построение и интерпретация общих факторов 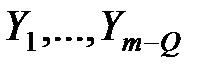 .
.
Но некоторые частные схемы конфлюэнтного анализа укладываются в рамках схемы регрессионного анализа, например если по наблюдениям надо выявить единственную зависимость переменной Х1, измеренной с ошибкой, от остальных переменных, измеренных без ошибок.
ПРИМЕРЫ ТЕСТОВ
1. Проверено 3000 электролампочек. Доля брака в этой партии составляет 0,15. Какова вероятность того, что отклонение установочной частоты брака от доли брака во всей продукции не превышает по абсолютной величине 0,01%? Выборку считать повторной.
2. Из партии в 800 деталей было подвергнуто проверке 12,5% деталей. Среди них оказалось 4% нестандартных. Определить вероятность того, что доля нестандартных деталей во всей партии отличается от выборочной доли не более чем на 1,5%.
3. С какой вероятностью можно утверждать, что ошибка средней арифметической 25 измерений не превзойдёт 0,04 см, если каждое измерение характеризовалось средним квадратическим отклонением 0,097 см?
4. Провели 11 наблюдений за временем обслуживания клиента в фирме. Получили следующие данные (мин):4,8; 3,8; 1,9; 4,7; 2,3; 2,8: 5,7; 2,2; 3,0; 3,5; 5,1. Найти параметр показательного закона распределения времени обслуживания клиента в фирме, используя метод квантилей.
5. На сколько процентов увеличится ошибка выборки при уменьшении процента отбора с 36% до 19% и неизменных дисперсии и объёме выборки?
6. При исследовании корреляционной зависимости между объёмом производства X и доходами от реализации продукции Y получены следующие уравнения регрессии: y = 0,3x + 120 и x = 1,6y – 88. Найти выборочный коэффициент корреляции между величинами X и Y.
7. Какая из представленных матриц может являться ковариационной матрицей переменных, для которых строится уравнение регрессии?
1) 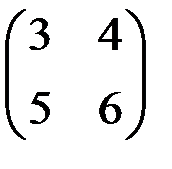 2)
2) 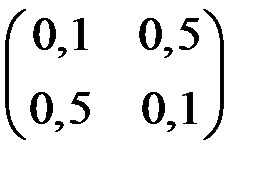 3)
3) 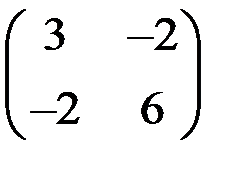 4)
4) 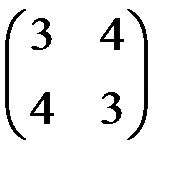 5)
5) 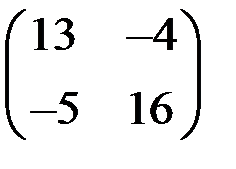 6)
6) 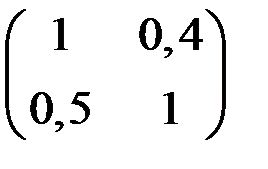 .
.
8. Доходы трёх банков от кредитов в отчётном году характеризуются следующими показателями:
| № банка | Процентная ставка | Доход (прибыль) банка, тыс. руб. |
| 1 | 22 | 900 |
| 2 | 15 | 1700 |
| 3 | 18 | 1400 |
Определить среднюю процентную ставку кредитов банков
9. Если известны уравнения регрессии
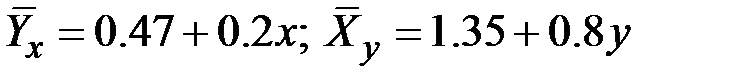 , то коэффициент корреляции равен:
, то коэффициент корреляции равен:
10. Обследовано 20% продукции предприятия. На сколько процентов ошибка собственно–случайной бесповторной выборки будет меньше ошибки повторной выборки?
11. Известны уравнения регрессии в виде  .
.
Чему равен коэффициент корреляции величин Х и Y?
12. Статистика показывает, что время обработки заявки на ЭВМ подчиняется показательному распределению со средним значением 3,5 мин. Чему равен коэффициент вариации времени обработки заявки на ЭВМ?
13. Сколько изделий необходимо обследовать, чтобы определить долю брака с точностью 2% при доверительной вероятности 0,954:
14. Провели 12 замеров случайной величины Х. Получили следующие основные характеристики: 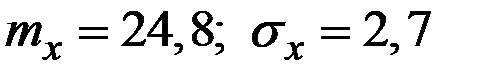 . Найти предельную ошибку среднего значения случайной величины Х с доверительной вероятностью 0,95.
. Найти предельную ошибку среднего значения случайной величины Х с доверительной вероятностью 0,95.
15. Средний балл 25 студентов первой группы составляет 4,3.
Средний балл 15 студентов первой группы составляет 3,9.
При каком максимальном уровне значимости можно считать эти баллы одинаковыми?
16. Связь между нормально распределёнными показателями Х и Y выражается зависимостью y = 1,2х + 0,5. При этом дисперсия Y в 4 раза выше дисперсии Х. Найти степень тесноты связи величин Х и Y .
17. По данным 2%–го выборочного обследования (n = 100) доля сотрудников коммерческих банков города, имеющих стаж работы в банке менее одного года, равна 10%. Ошибка выборки для доли рабочих, имеющих стаж работы в банке менее одного года, с вероятностью 0,954 равна (в процентах):
18. При исследовании корреляционной зависимости между объёмом валовой продукции Y (млн. руб.) и среднесуточной численностью работающих Х (тыс. чел) для ряда предприятий отрасли получено следующее уравнение регрессии Х и Y: ху = 0,2у – 2,5. Средний объём валовой продукции предприятий составил 40 млн. руб. Найти значение среднесуточной численности работающих на предприятиях.
19. Сколько надо произвести опытов, чтобы с вероятностью 0,9 получить коэффициент корреляции с точностью 0,2?
20. Известны основные числовые характеристики величин  :
:
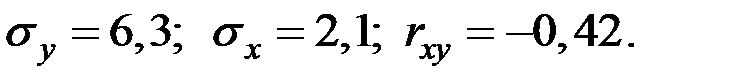
Найти коэффициент линейной регрессии  от Х имеет значение.
от Х имеет значение.
21. Общая сумма квадратов отклонений 55 наблюдений величины Х составила величину 144. Остаточная сумма квадратов отклонений наблюдений величины Х от уравнения регрессии 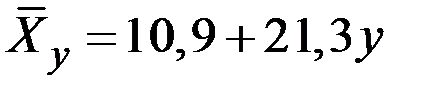 составила величину 36. Чему равна точность модели регрессии?
составила величину 36. Чему равна точность модели регрессии?
22. Дисперсии двух независимых СВ (X, Y) соответственно равны 9 и 16. Величина Z = X + Y . Найти коэффициент корреляции величин (Y,Z).
23. По выборке объёмом n получены уравнения регрессии в виде
 .
.
При каком n эти уравнения значимы при уровне значимости a = 0,05?
24. По выборке из 46 наблюдений за тремя показателями вычислены парные коэффициенты корреляции:  .
.
Вычислить множественный коэффициент корреляции зависимости первого показателя от остальных.
25. По выборке из 72 наблюдений за тремя показателями вычислены парные коэффициенты корреляции: 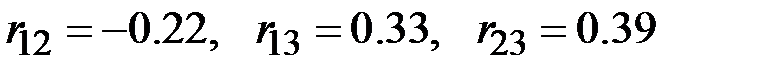 . Частный (парциальный) коэффициент корреляции первых двух показателей равен
. Частный (парциальный) коэффициент корреляции первых двух показателей равен
26. При исследовании корреляционной зависимости между объёмом производства X и доходами от реализации продукции Y получены следующие уравнения регрессии: y = 0,3x + 120 и x = 1,6y – 88. Найти выборочный коэффициент корреляции между величинами X и Y.
27. По статистике среднедушевые доходы по региону за два квартала года составили соответственно 140 и 150 тыс. руб. Потребление мясных продуктов за эти периоды характеризуются величинами 22 и 20 кг/чел. Потребление овощей и фруктов за эти периоды характеризуются величинами 75 и 81 кг/чел. Чему равен коэффициент эластичности потребления мясных продуктов в зависимости от дохода?
28. По выборке объёмом n был найден ранговый коэффициент корреляции Спирмена, равным 0,5. При каком n ранговый коэффициент корреляции Спирмена значим при уровне значимости a = 0,05?
29. По выборке объёмом n при работе четырёх экспертов вычислен коэффициент конкордации, равным 0,55. При каком n коэффициент конкордации значим при уровне значимости a = 0,05?
30. На трёх уровнях качественного показателя измерены значения количественного показателя Х. Сумма квадратов отклонений наблюдений величины Х по уровням составила величину 8,6. Остаточная сумма квадратов отклонений наблюдений величины Х составила величину 17. При каком количестве наблюдений можно сделать вывод о том, что качественный показатель влияет на количественный при уровне значимости a = 0,05?
31. Общая сумма квадратов отклонений 25 наблюдений величины Х составила величину 186. Остаточная сумма квадратов отклонений наблюдений величины Х от уравнения регрессии 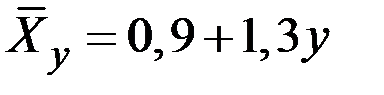 составила величину 57. Чему равен коэффициент детерминации?
составила величину 57. Чему равен коэффициент детерминации?
32. Известны основные числовые характеристики величин  :
:
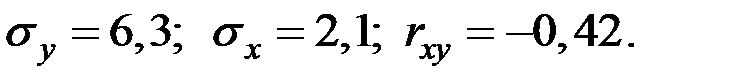
Тогда коэффициент линейной регрессии  от Х имеет значение:
от Х имеет значение:
33. Общая сумма квадратов отклонений 35 наблюдений величины Х составила величину 144. Остаточная сумма квадратов отклонений наблюдений величины Х от уравнения регрессии 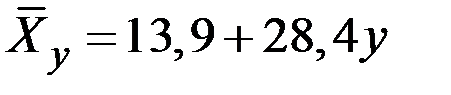 составила величину 46. Чему равна точность модели регрессии?
составила величину 46. Чему равна точность модели регрессии?
34. Известны основные числовые характеристики величин 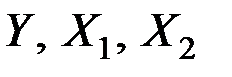 :
:
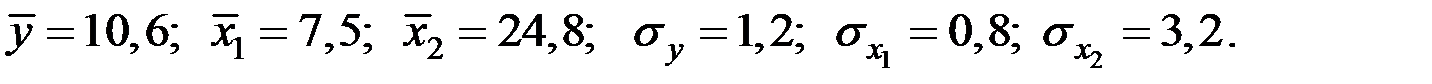
Уравнение множественной регрессии имеет вид:
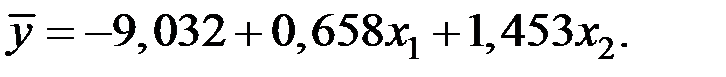
Чему равен коэффициент эластичности для 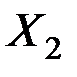 ?
?
35. По выборке объёмом n был найден индекс корреляции (корреляционное отношение) 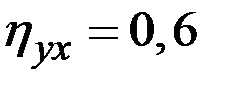 . При каком n индекс значим при уровне значимости a = 0,05?
. При каком n индекс значим при уровне значимости a = 0,05?
36. Числовые характеристики исследуемых показателей следующие:
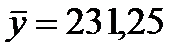 ;
; 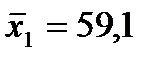 ;
; 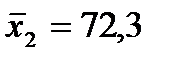 ;
; 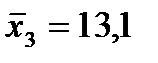 ;
;
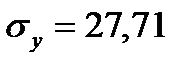 ;
; 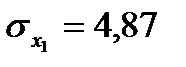 ;
; 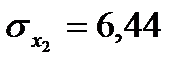 ;
; 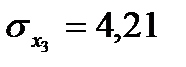 .
.
Уравнение множественной регрессии имеет вид:
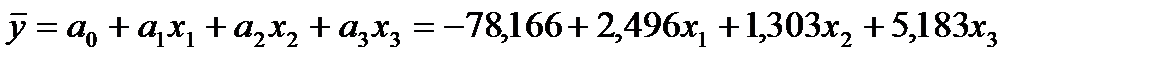 .
.
Вычислить стандартизированный коэффициент регрессии показателя Х1.
37. Два товароведа расположили девять мотков пряжи в порядке убывания качества окраски нити. Получены две последовательности рангов:
| xi | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| yi | 4 | 1 | 5 | 3 | 2 | 6 | 9 | 8 | 7 |
Найти коэффициент корреляции Спирмена между рангами xi и yi
38. Известны основные числовые характеристики величин 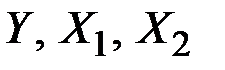 :
:
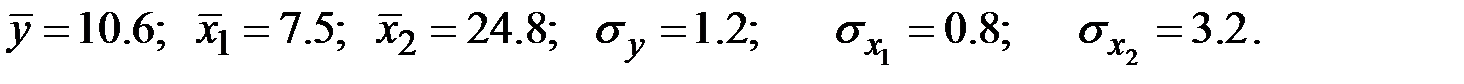
Уравнение множественной регрессии имеет вид

Коэффициент эластичности для 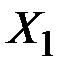 равен
равен
39. Известны основные числовые характеристики величин 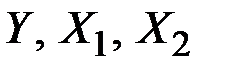 :
:
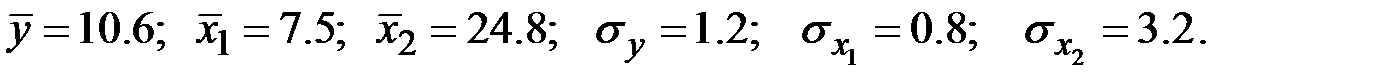
Уравнение множественной регрессии имеет вид

Чему равен коэффициент эластичности для 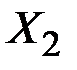 ?
?
40. При приёме на работу семи кандидатам было предложено два теста. Результаты тестирования (в баллах) приведены в таблице:
|
Тест | Кандидат | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 31 | 82 | 25 | 26 | 53 | 30 | 29 |
| 2 | 21 | 55 | 8 | 27 | 32 | 42 | 26 |
Вычислить ранговый коэффициент корреляции Спирмена.
41. Числовые характеристики исследуемых показателей следующие:
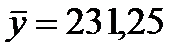 ;
; 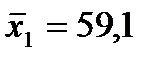 ;
; 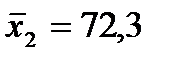 ;
; 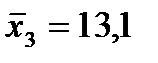 ;
;
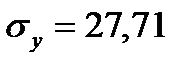 ;
; 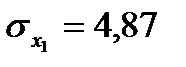 ;
; 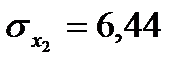 ;
; 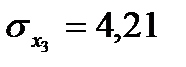 .
.
Уравнение множественной регрессии имеет вид:
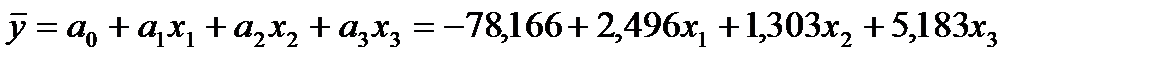 .
.
Вычислить коэффициент эластичности показателя Х3.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика. Основы моделирования и первичная обработка данных. – М.: Финансы и статистика. 1983. – 471 с.
2. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. – М.: ЮНИТИ, 1998. – 1022 с.
3. Браилов А.В., Зададаев С.А., Рябов П.Е. Практикум для самостоятельной работы студентов по дисциплине «Теория вероятностей и математическая статистика». М.: Финуниверситет, 2014. – 206 с.
4. Енюков И.С. Методы, алгоритмы, программы многомерного статистического анализа. – М.: Финансы и статистика, 1986. – 232 с.
5. Ивченко Г.И., Медведев Ю.И. Математическая статистика. – М.: Высшая школа, 1984. – 248 с.
6. Колемаев В.А., Староверов О.В. Турундаевский В.Б. Теория вероятностей и математическая статистика/ Учеб. пособие. Под ред. В.А. Колемаева. – М.: Высшая школа, 1991. – 400 с.
7. Кочетыгов А.А. Статистика. Учебное пособие. Тула: ТулГУ, 2003. – 292 с.
8. Кочетыгов А.А. Тория вероятностей. Учебное пособие. Тула: ТулГУ, 2016. – 234 с.
9. Кочетыгов А.А. Тория вероятностей и математическая статистка. Учебное пособие. Тула: ТулГУ, 2006. – 320 с.
10. Кочетыгов А.А. Математическая статистика. Решение задач с использованием пакета SPSS: Учеб. пособие/Тула: Изд–во ТулГУ, 2011. –156 с.
11. Кочетыгов А.А., Толоконников Л.А. Эконометрика. Учебное пособие. Тула: ТулГУ, 2006. – 320 с.
12. Кочетыгов А.А., Толоконников Л.А. Основы эконометрики. Учебное пособие. – М: ИКЦ «Март». 2007. – 344 с.
13. Кочетыгов А.А. Случайные процессы: Учеб. пособие. – Тула: Изд–во Тул. гос. ун–та. 2000. – 308 с.
14. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник. – М.: ЮНИТИ–ДАНА, 2000. – 543 с.
15. Мелихов М.Б., Кочетыгов А.А. Моделирование и анализ стохастических процессов в экономике: Учебное пособие для вузов. – М.: Изд–во МГУК, 2000. – 363 с.
16. Христич Д.В. Теория вероятностей и математическая статистика: учеб. пособие / – Тула, Изд–во ТулГУ, 2011. – 226 с.
ПРИЛОЖЕНИЕ
Дата: 2019-03-05, просмотров: 1643.