Метод главных компонент
В компонентном анализе вычисляются главные компоненты, т.е. некоррелированные комбинации исходных показателей, сохраняющие их общую дисперсию без изменений.
Определение главных компонент (ГК) производится по корреляционной матрице исходных показателей. Результатом компонентного анализа на ЭВМ являются дисперсии главных компонент, их доли в общей дисперсии и сами главные компоненты.
Другими словами, метод главных компонент (МГК) позволяет по заданной (вычисленной) m–мерной корреляционной матрице R исходных показателей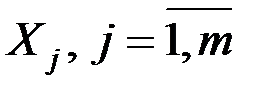 
найти новую ортогональную m–мерную систему координат 
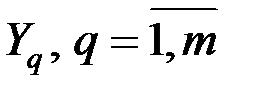и именно так, чтобы максимум полной дисперсии лежал в направлении первой главной оси, а максимум оставшийся дисперсии – в направлении второй главной оси и т.д. (рис. 6.1).
| Y |
| 1 |
| Y |
| 2 |
| Y |
| m |
|
|
|
|
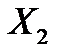
Рис. 6.1. Графическое представление преобразования
в методе главных компонент
Процедуру вычисления последовательностей осей можно прекратить в любом месте и, например, выбрать только две первые главные компоненты, которые воспроизводят, например, лишь 80% полной дисперсии.
Главные компоненты представляют собой новое множество показателей 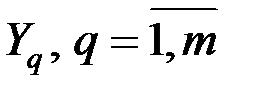, которые обладают следующими свойствами.
1. Каждая главная компонента (новый фактор) является линейной комбинацией исходных нормированных показателей:
Здесь А = {аjq} – матрица нагрузок показателей на ГК;
– собственные числа матрицы R.
2. Все главные компоненты статистически независимы друг от друга, т.е. Cov[Y k, Y р] = 0, при k № р.
3. ГК упорядочиваются по их дисперсиям:
D[Y1] і D[Y2] і ... і D[Ym].
4. Дисперсии D[Y q] являются собственными числами корреляционной матрицы R, а матрица преобразования AТ состоит из собственных векторов матрицы R.
Число l j, являющееся корнем уравнения |R – l jЕ| = 0 называется собственным числом или собственным значением матрицы R.
Здесь Е – единичная матрица (все элементы нулевые, кроме диагональных, равных 1).
Для матрицы R величины l j будут действительными положительными числами.
Любой вектор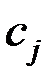 
единичной длины, являющийся решением системы 
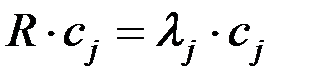, называется собственным вектором матрицы R, соответствующим собственному числу 
.
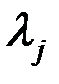5. Поскольку у корреляционной матрицы имеется лишь одно множество отличных от нуля собственных чисел, то переход к ГК определяется однозначно.
6. При переходе к ГК сумма дисперсий всех показателей остаётся неизменной:
.
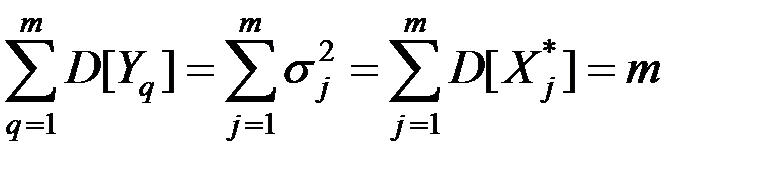7. Исходные нормированные показатели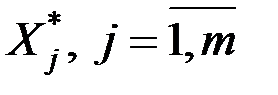 
выражаются через новые 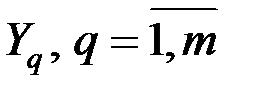по следующей матричной зависимости: 
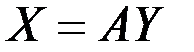, или в другом виде
,
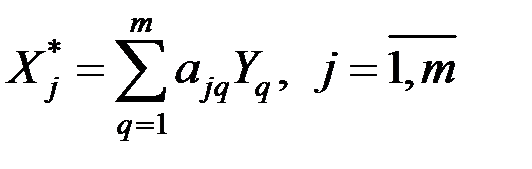где 
– матрица значений ГК для наблюдений.
Пусть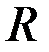 
– корреляционная матрица стандартизованный показателей.
Тогда, в соответствии с определением, дисперсия вектор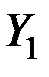а 
равна
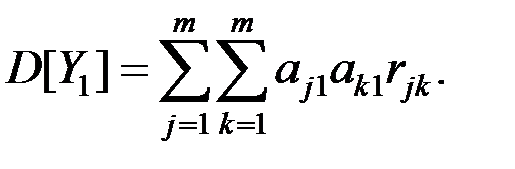
Необходимо найти вектор–столбец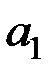 
, который максимизирует эту дисперсию при условии 
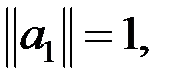которое обеспечивает единственность решения.
Выражение для дисперсии можно переписать в эквивалентной форме в виде скалярного произведения
Решением этого соотношения является максимальное собственное значение матрицы 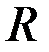и соответствующий ему собственный вектор 
.
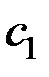Аналогично находятся остальные ГК.
Таким образом, первые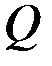 
главных компонент объясняют
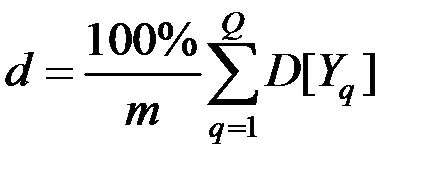
процентов дисперсии исходных переменных.
На практике обычно ограничиваются таким числом компонент, при котором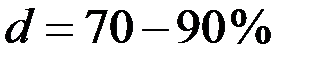 
.
При этом условии число ГК получается значительно меньшим числа исходных показателей, что облегчает процесс анализа данных.
Коэффициенты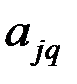 
главных компонент определяются по формуле
где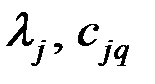 
– собственное значение матрицы и соответствующий ему собственный вектор применительно к j–й ГК.
Исходя из значений коэффициентов главных компонент можно ранжировать факторы по степени их значимости в главной компоненте.
Можно вычислить индивидуальные значения главных компонент (для каждого наблюдения) и использовать их в дальнейшем для построения уравнения регрессии для исходных показателей.
6.2.2. Факторный анализ – это способ приведения (синтеза) множества непосредственно наблюдаемых показателей 
к меньшему числу Q < m новых линейно независимых факторов (признаков, показателей, главных компонент)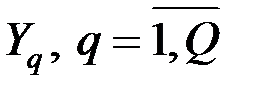 
.
Пусть исходные данные представлены в виде матрицы
),
где n – количество наблюдений,
m – количество показателей.
Так как величины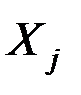 
могут иметь различный физический смысл и различные шкалы измерений, удобнее перейти к стандартизированной матрице исходных данных
.
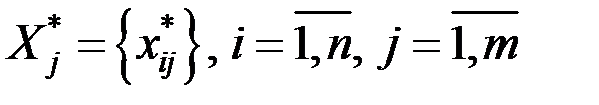В факторном анализе предполагается линейная связь между измеряемыми нормированными показателями и факторами:
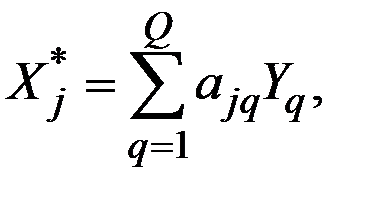
где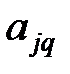 
– подлежащиe определению коэффициенты.
В факторном анализе возникают несколько проблем (рис. 6.2).
1. Проблема общности состоит в определении доли дисперсии показателя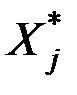 
, обусловленной общностью ( 
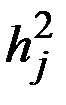). Оценка 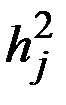должна быть определена до выделения факторов, что и составляет проблему.
2. Проблема факторов состоит в установлении числа и вида новых осей координат 
, необходимых для отображения m переменных.
Здесь применяются три основные модели: модель главных компонент, модель центроидных компонент и факторная модель.
При любых способах решения проблемы факторов вводятся различные ограничения для однозначного решения системы равенств
R = А AT + U2,
где AT – транспонированная матрица факторных нагрузок;
U2 – специфичность исходных показателей.
Процедура выделения факторов имеет бесконечно много эквивалентных решений, которые одинаково хорошо удовлетворяют равенству
Rh = А AT.
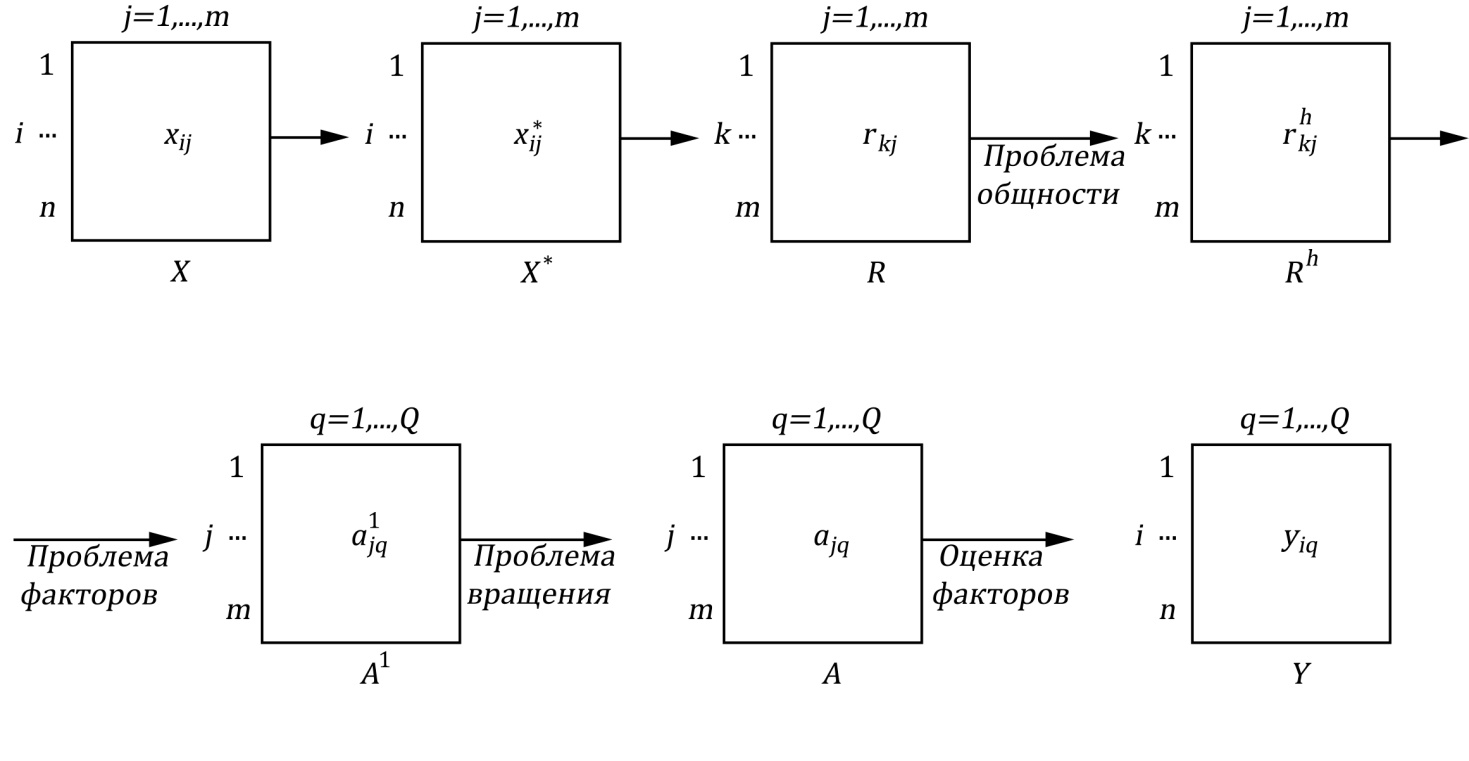Рис. 6.2. Последовательность действий
при проведении факторного анализа
Здесь X = {xij} – матрица исходных данных;
i = 1, 2, ..., n – наблюдения (объекты);
j = 1, 2, ..., m – переменные;
X* = {x*ij} – стандартизированная матрица исходных данных;
R = {r k j} – корреляционная матрица показателей;
Rh = {rh k j} – редуцированная корреляционная матрица;
А1 = {а1jq} – первичная матрица факторных нагрузок;
q = 1, 2, ..., Q – факторы;
А = {аjq} – факторная матрица после поворота осей;
Y = {yjq} – матрица значений факторов.
3. При решении проблемы вращения речь идёт о том, чтобы в уже установленном нами пространстве общих факторов дать каждой новой переменной наиболее простое факторное объяснение (максимальные нагрузки для одних факторов, минимальные для других).
Конечным результатом факторного анализа является получение содержательно интерпретируемых факторов , воспроизводящих матрицу коэффициентов корреляции между исходными переменными.
Для отдельного наблюдения (объекта) имеем
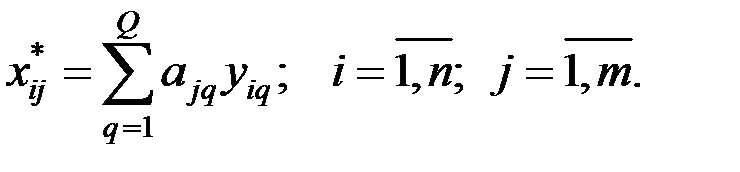
Здесь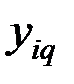 
– значение фактора q у i–го объекта.
4. Измерение факторов осуществляется, исходя из равенства:
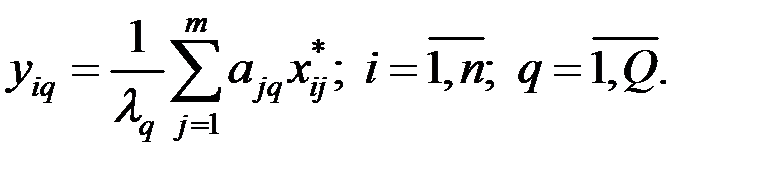
Здесь – собственные числа матрицы R.
Существенное отличие МГК от факторного анализа заключается в том, что диагональные элементы матрицы R, используемые в МГК, каждый раз равны единице.
Это означает, что общности равны единице, т.е. характерные факторы отсутствуют.
Пример 6.1. Для 27 предприятий города методом главных компонент исследовать взаимосвязь трёх показателей: выработка (тыс. руб.) на одного среднегодового работника ( 
); уровень рентабельности (%) предприятия ( 
); фондоотдача (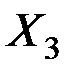 
,%).
Решение. Технологию использования метода главных компонент продемонстрируем на условных данных.
1. Пусть стандартизованная матрица исходных данных имеет вид:
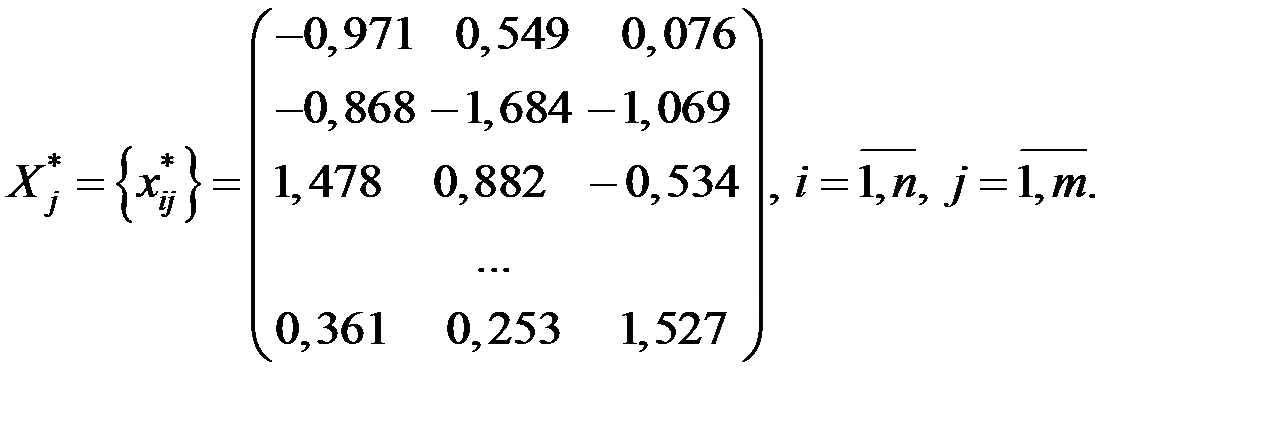
Размерность матицы: n = 27; m = 3.
2. Обработка матрицы наблюдений дала следующую матрицу коэффициентов корреляции (k = 1, 2,..., m; j = 1, 2,..., m):
3. Определитель этой матрицы
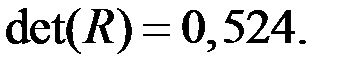
4. Найдём собственные числа матрицы R.
Число l j, являющееся корнем уравнения |R – l jЕ| = 0 называется собственным числом или собственным значением матрицы R. Здесь Е – единичная матрица (все элементы нулевые, кроме диагональных, равных 1).
Составим характеристическое уравнение
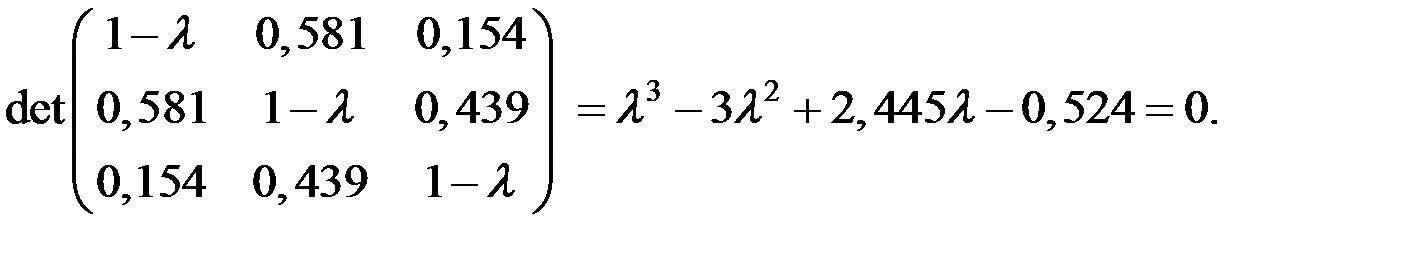
Отсюда: 
Это означает, что главная компонента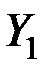 
объясняет 1,798/3 = 59,9% всей вариации исходных показателей. 
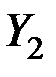объясняет 0,875/3 = 29,2%, а 
0,327/3 = 10,9% всей вариации исходных показателей.
5. Найдём собственные векторы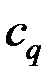 
матрицы R, соответствующие собственным числам 
Любой вектор 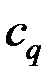единичной длины, являющийся решением системы 
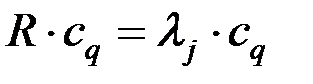, называется собственным вектором матрицы R, соответствующим собственному числу
Каждый вектор 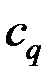имеет компоненты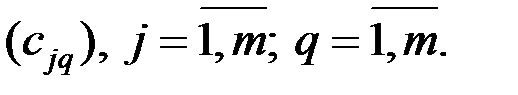 
Для вектора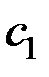 
имеем систему уравнений
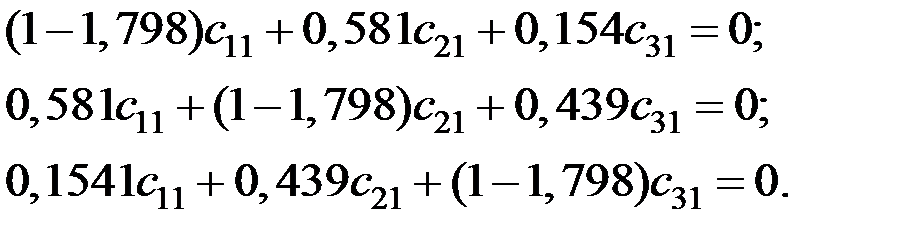
Получаем компоненты вектора :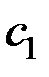
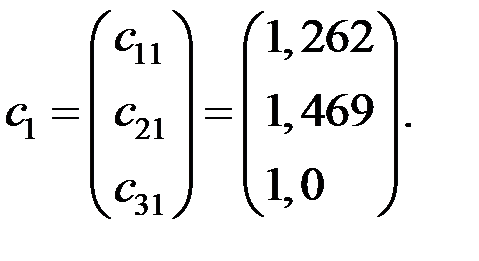
Для вектора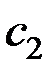 
имеем систему уравнений
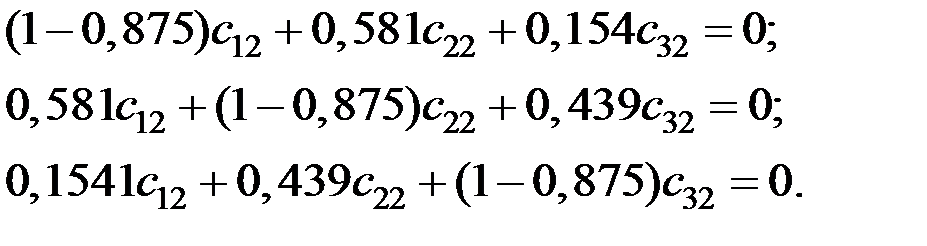
Получаем компоненты вектора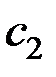 
:
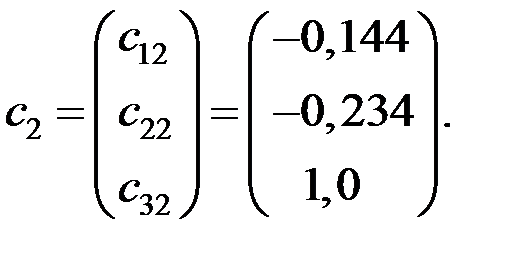
Для вектора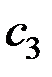 
имеем систему уравнений
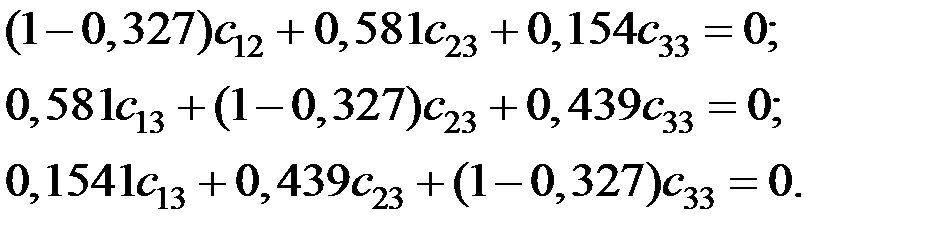
Получаем компоненты вектора :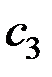
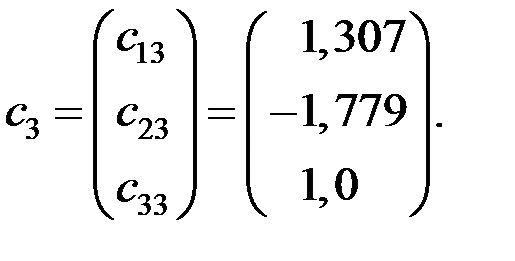
Матрица собственных векторов принимает вид:
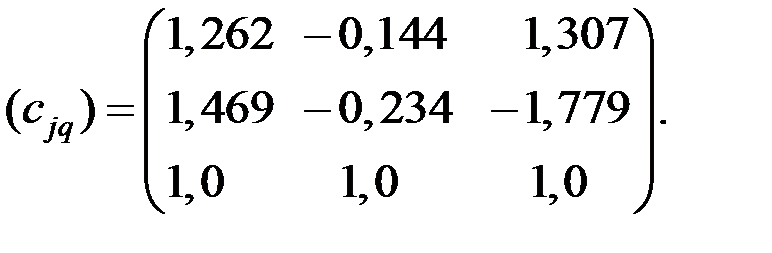
6. Пронормируем векторы 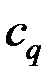. Найдём векторы
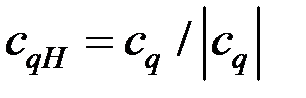
и получим матрицу нормированных собственных векторов 
.
Получаем:
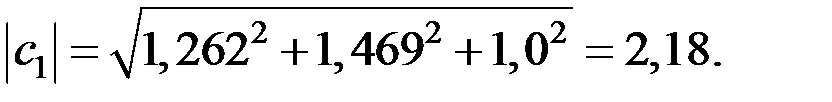
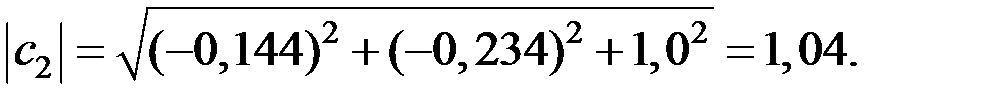
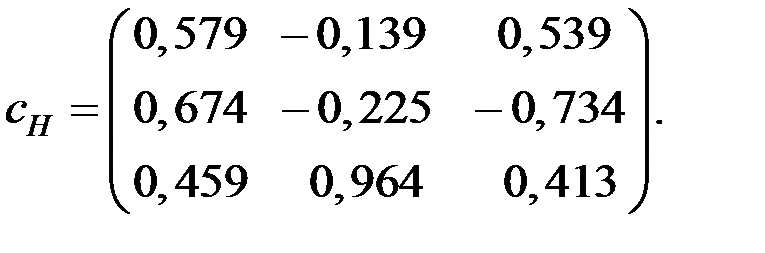
Должно выполняться условие
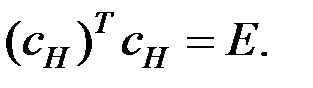
Проверяем:
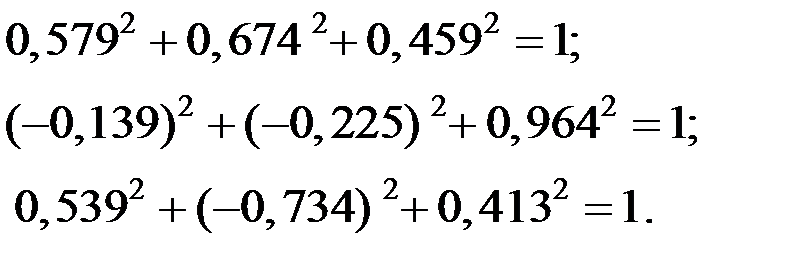
7. Матрицу факторного отображения А получаем из уравнения:
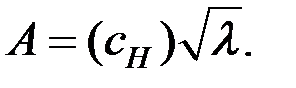
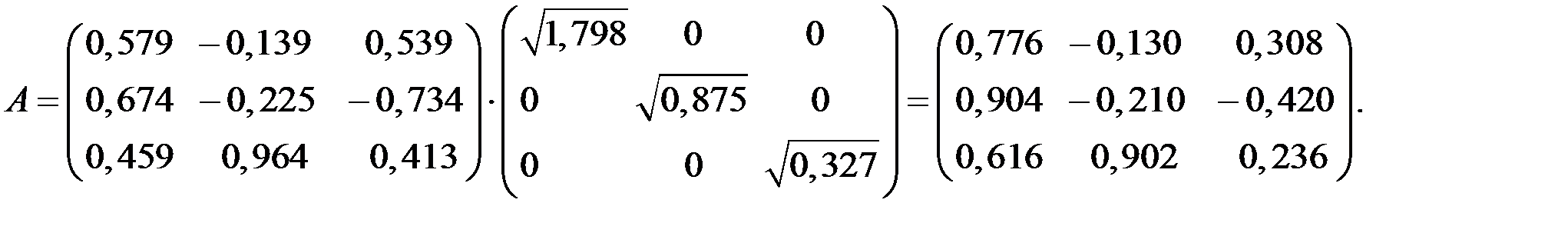
Матрица факторного отображения А содержит частные коэффициенты корреляции, представляющие связи исходных показателей и главных компонент.
Из равенства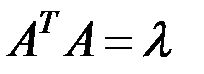 
следует условие
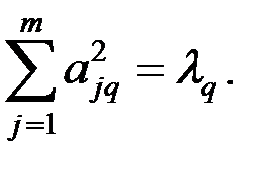
Проверяем:
8. Система уравнений взаимосвязи нормированных показателей (опустим * у обозначения) 
и 
и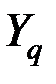меет вид:
9. Система уравнений взаимосвязи показателе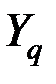й и выражается через матрицу А и собственные числа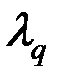 
по соотношению
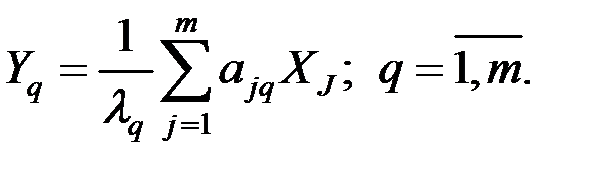
Получаем:
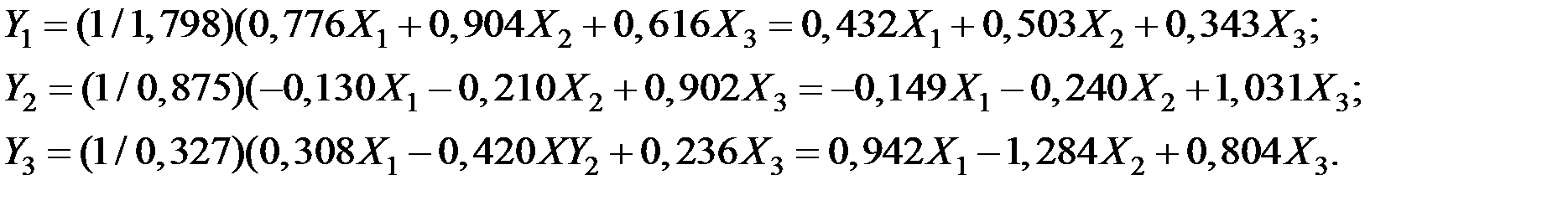
10. В матричном виде имеем соотношения:
Получаем:
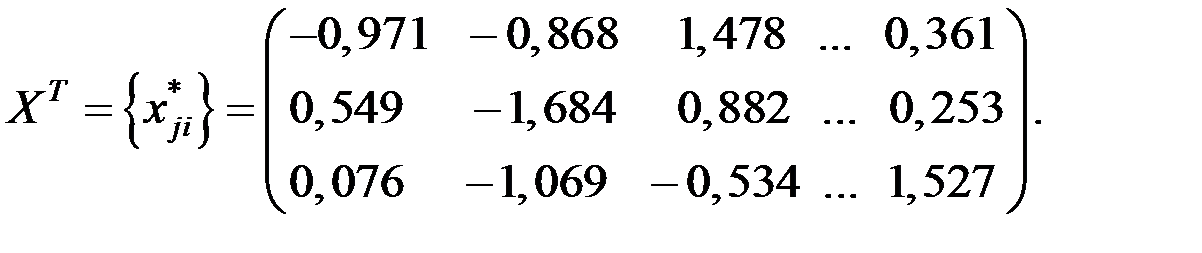
Пример 6.2. Исследовать взаимосвязь результатов спортсменов по 4 видам спорта: прыжкам в высоту, прыжкам в длину, бегу на 400 метров, поднятию штанги. Для этого провели наблюдение за 25 спортсменами. Получили матрицу наблюдений:
X = {xij}, i = 1, 2, ..., n; j = 1, 2, ..., m; n = 25; m = 4.
Обработка матрицы наблюдений дала следующую матрицу коэффициентов корреляции (k = 1, 2,..., m; j = 1, 2,..., m):
.
Проанализировать имеющиеся коэффициенты корреляции с применением метода факторного анализа.
Решение. Наблюдаемые коэффициенты корреляции можно попытаться воспроизвести с помощью следующего уравнения: R = A AT.
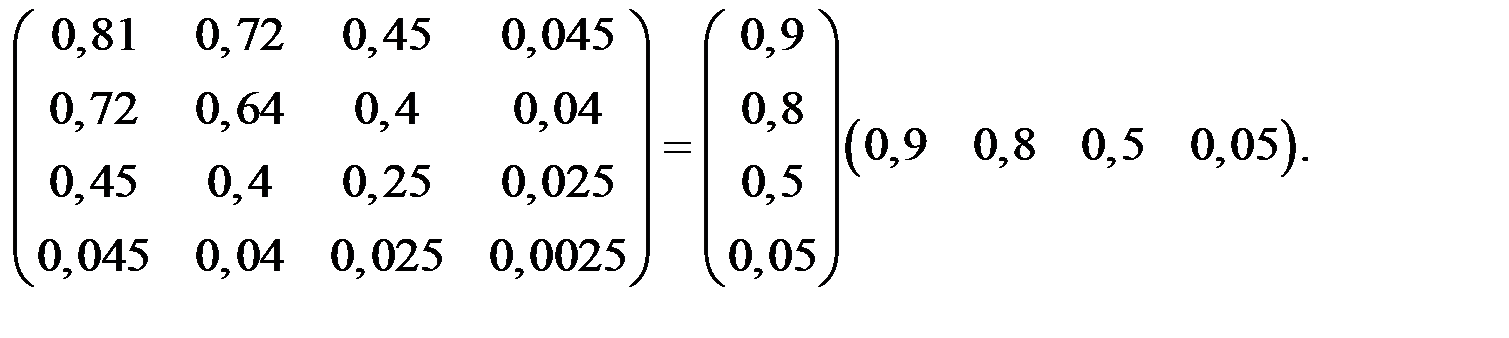
Здесь A – факторные нагрузки на исходные показатели (диагональные элементы – общности).
Равенство даёт основание полагать (предполагать), что за наблюдаемыми корреляциями стоит фактор, который мог бы причинно обусловить эти корреляции.
Десять различных значений элементов корреляционной матрицы привели к четырём элементам матрицы (вектора) А.
Эти четыре значения содержат ту же самую информацию, что и вся корреляционная матрица, т.е. достигается упрощение, причём объём информации сохраняется (рис. 6.3).
Факторные нагрузки соответствуют коэффициентам корреляции, т.е. переменная Х1 имеет много общего с фактором Y1 (а11 = 0,9) и т.д.
Геометрически упрощение заключается в том, что единственная мера, а именно фактор Y1, достаточна для отображения связей между переменными.
В этом примере все переменные (все стрелки) примут одно направление, а именно направление фактора Y, который рассматривается как координатная ось новой полученной одномерной системы координат
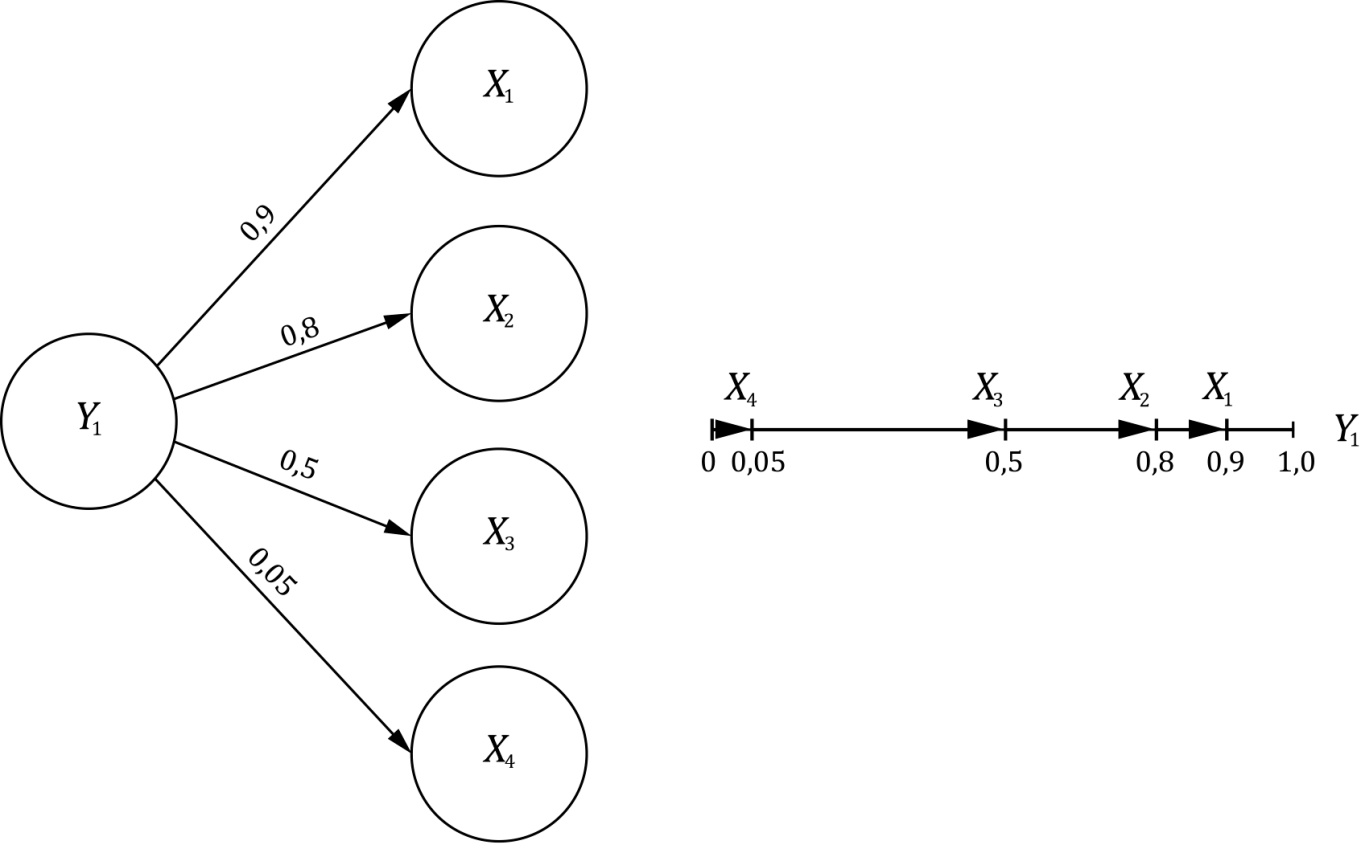
Рис. 6.3. Геометрическая интерпретация решения задачи
Пример 6.3. Исследовалась взаимосвязь результатов спортсменов по 4 видам спорта: прыжкам в высоту, прыжкам в длину, толканию ядра, поднятию штанги. Для этого провели наблюдение за 30 спортсменами (в отличие от примера 6.2 заменили бег на 400 м толканием ядра).
Получили следующую корреляционную матрицу:
.
Проанализировать имеющиеся коэффициенты корреляции с применением метода факторного анализа.
Решение.
Первый фактор Y1 = (0,9; 0,8; 0,05; 0,05) может объяснить следующие корреляции
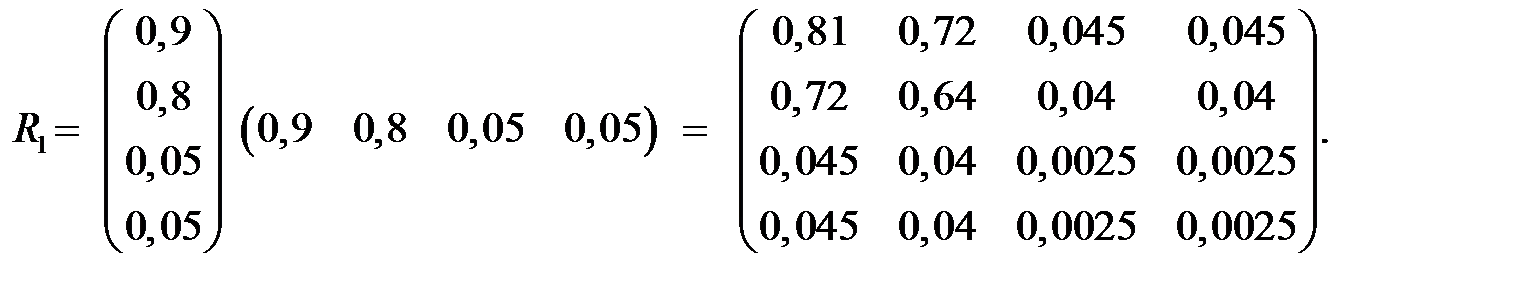
Остаточная матрица Rост = R – R1 (за исключением диагональных элементов) может быть объяснена вторым фактором
Y2 = (0,05; 0,05; 0,8; 0,7).
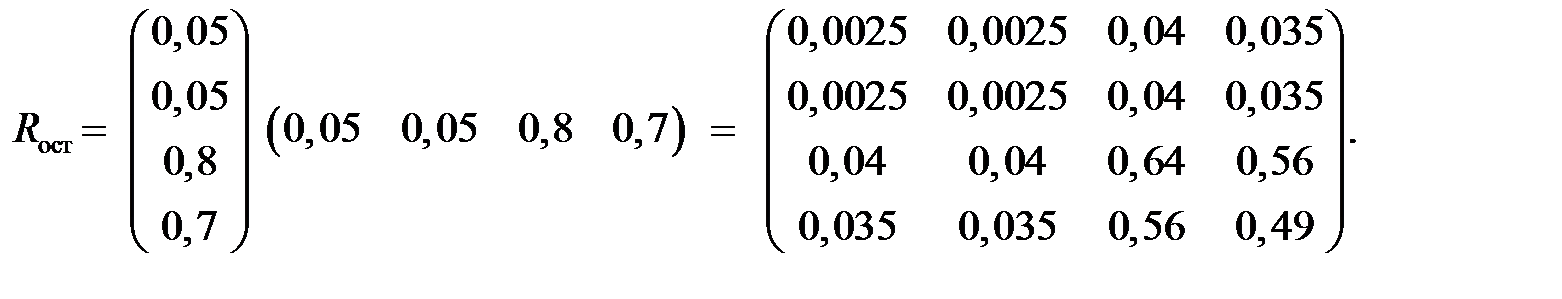
Окончательно получим
Rh = A AT:
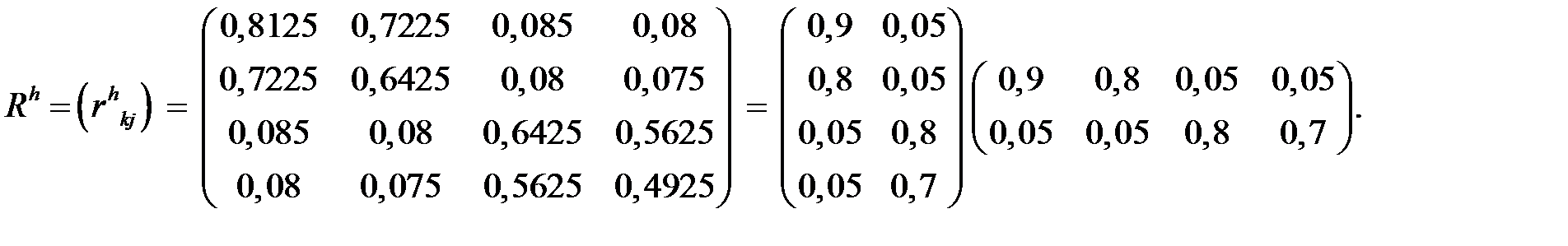
От четырёх наблюдаемых переменных Х перешли к двум новым факторам Y (неизвестной природы) (рис. 6.4).
Достигнуто определённое сжатие информации (работать с двумя показателями легче, чем с четырьмя).
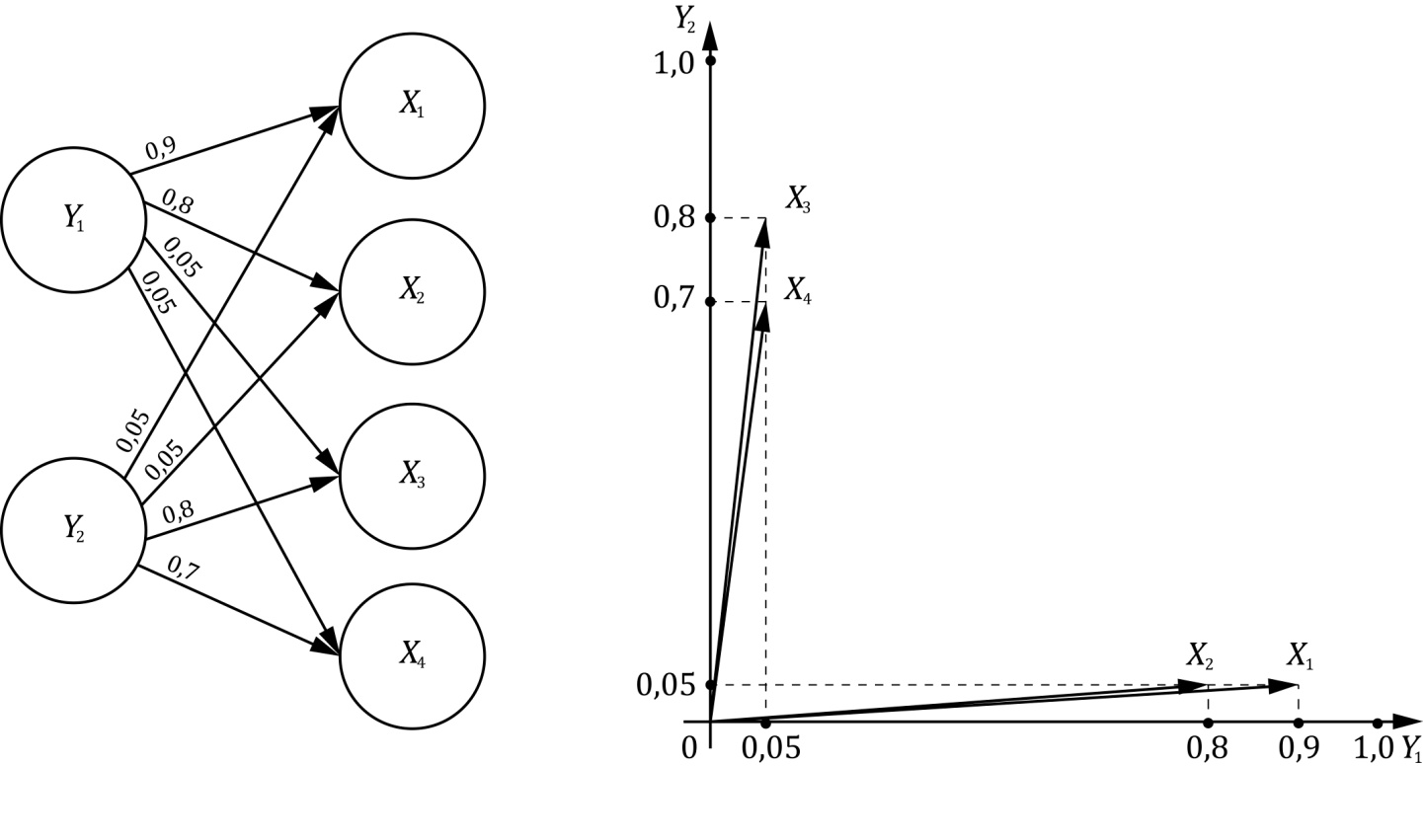
Рис. 6.4. Геометрическая интерпретация решения задачи
для двух факторов
Новые показатели (факторы) ещё не обладают физической интерпретацией. Если бы мы научились измерять их, то мы могли бы отказаться от исходных четырёх показателей и перейти к двум новым.
Здесь можно выдвигать различные гипотезы о смысле Y.
Условно можно называть Y1 "прыгучесть" спортсмена, т.к. этот показатель определяет на 90% результаты в высоту и на 80% в длину, а показатель Y2 – в основном определяет результаты по толканию ядра и по штанге, и может быть условно назван " мощь (мощность)" спортсмена.
Если даже мы не сможем физически интерпретировать Y, то польза от них может быть в чисто прикладном аспекте, например, при классификации спортсменов по группам, т.к. классифицировать по двум показателям легче, чем по четырём.
Пример 6.4. По 52 предприятиям города собраны данные по 5 показателям: X1 - коэффициент сменности оборудования; X2 - среднегодовая численность персонала; X3 - среднегодовая стоимость фондов; X4 - среднегодовой фонд заработной платы персонала; X5 - непроизводственные расходы. Ниже приведена сокращённая матрица исходных данных:
| № предприятия | X1 | X2 | X3 | X4 | X5 |
| 1 | 1,37 | 26006 | 167,69 | 47750 | 17,72 |
| 2 | 1,49 | 23935 | 186,1 | 50391 | 18,39 |
| 3 | 1,44 | 22589 | 220,45 | 43149 | 26,46 |
| … | … | … | … | … | … |
| 52 | 1,22 | 11795 | 78,11 | 22225 | 19,41 |
Обработать имеющиеся данные методом факторного анализа.
Решение. Проведём анализ с помощью пакета SPSS 12.0 (Анализ – Обработка данных – Факторный анализ – Метод главных компонент).
Ниже приведены результаты работы программы факторного анализа.
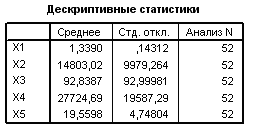
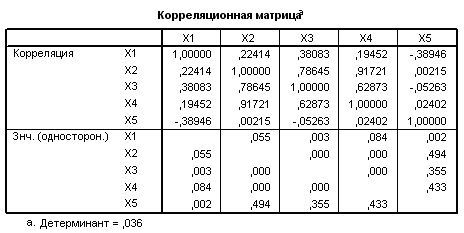
Можно выбрать две главные компоненты, вклад которых в дисперсию изучаемых признаков составляет 80,486%.
Матрица факторных нагрузок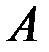 
имеет вид:
| 0,4529 | – 0,70957 | 0,50413 | – 0,1925 | – 0,0126 |
| 0,9518 | 0,209987 | – 0,13638 | – 0,0448 | – 0,17286 |
| 0,87961 | 0,0070 | 0,14787 | 0,4490 | 0,0635 |
| 0,89274 | 0,241139 | – 0,19001 | – 0,3054 | 0,1277 |
| – 0,11816 | 0,85149 | 0,50643 | – 0,0663 | – 0,0045 |
Матрица главных компонент будет иметь вид:
| № предприятия |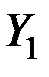
| 
| 
| 
| 
|
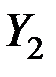
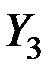
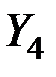
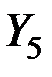
| 1 | 1,061 | 0,004 | –0,541 | –0,052 | –0,270 |
| 2 | 1,2335 | –0,3635 | 0,3639 | –0,391 | 0,819 |
| 3 | 1,0496 | 0,8351 | 1,787 | 0,323 | 0,7429 |
| … | … | … | … | … | … |
| 52 | –0,3935 | 0,32689 | –0,6269 | 0,5681 | 0,3388 |
Приведём пример возможного использования факторного анализа для оценки финансово–экономического состояния предприятий, прогноза их развития и перспектив выхода из кризиса на основе экономического анализа статей бухгалтерского баланса.
Рассматривалась система 12 коэффициентов несостоятельности :
К1 – коэффициент текущей ликвидности;
К2 – коэффициент обеспеченности собственными средствами;
К3 – коэффициент восстановления (утраты) платёжеспособности;
К4 – коэффициент покрытия; К5 – коэффициент автономии;
К6 , К7 – коэффициенты рентабельности активов и оборота;
К8 , К9 , К10 – коэффициенты оборотов дебиторской, кредиторской задолженности и оборотов готовой продукции и товарных запасов;
К11 – коэффициент напряжённости кредиторской задолженности;
К12 – коэффициент напряжённости задолженности в бюджет.
Коэффициенты К1 – К12 вычислялись по данным стандартных форм бухгалтерского баланса по определённым формулам.
Факторный анализ позволил сжать информацию, содержащуюся в 12 показателях (коэффициентах несостоятельности), без существенной потери в 4 фактора несостоятельности: Y1 – фактор оборачиваемости средств; Y2 – фактор финансовой устойчивости; Y3 – фактор автономии; Y4 – фактор обслуживания задолженности.
Полученные 4 фактора с учётом экспертных оценок их важности образовали с помощью линейной свёртки единый показатель несостоятельности, что весьма удобно для экспресс–анализа совокупности многих предприятий (и их классификации по единому показателю).
Дискриминантный анализ
Основные понятия
Дискриминантный анализ – это общий термин, относящийся к нескольким тесно связанным статистическим процедурам.
Эти процедуры можно разделить на методы интерпретации межгрупповых различий и методы классификации наблюдений (объектов) по группам.
Основным предположением дискримнантного анализа является то, что существуют две или более группы (классы, таксоны, кластеры, множества, совокупности), которые по некоторым параметрам отличаются между собой.
Основная задача дискриминантного анализа часто состоит в определении по результатам наблюдений, какой из возможных групп принадлежит объект, случайно извлечённый из одной из них. Метод используется, когда информация об истинной принадлежности объекта недоступна, требует разрушения объекта или чрезмерных материальных затрат и времени.
Основные ограничения, касающиеся статистических свойств дискриминантных переменных, т.е. показателей, с помощью которых описываются объекты в группах, сводятся к следующему.
1. Ни одна переменная 
не может быть линейной комбинацией других переменных.
2. Ковариационные матрицы дискриминантных переменных 
для генеральных совокупностей равны между собой для различных групп.
Это обеспечивает возможность использования для принятия решений о классификации линейных дискриминантных функций.
3. Закон распределения дискриминантных переменных для каждого класса является многомерным нормальным, т.е. каждая переменная имеет нормальное распределение при фиксированных остальных переменных. Данное предположение позволяет получить точные значения вероятности принадлежности объектов к данной группе и критерия значимости.
Пусть имеются две или более генеральные совокупности 
с известными (или оцениваемыми по выборкам) распределениями.
Получена реализация какой–то из рассматриваемых многомерных СВ, характеризующих соответствующую совокупность.
Задача дискриминации (различения, идентификации) состоит в построении правила, позволяющего приписать полученную реализацию (или объект) к определённой совокупности, т.е. идентифицировать этот новый объект.
Решение задачи дискриминации состоит в разбиении всего выборочного пространства всех возможных реализаций изучаемых СВ на некоторое число областей.
При попадании идентифицируемого объекта в соответствующую область этот объект приписывается к соответствующей генеральной совокупности.
Границы указанных областей должны быть по возможности простыми (например, гиперплоскостями) и выбраны таким образом, чтобы уменьшить потери от ложной дискриминации.
Часто информация о распределениях генеральных совокупностей представлена независимыми выборками из них.
Такие выборки называются обучающими выборками.
Рассмотрим две нормально распределённые m–мерные генеральные совокупност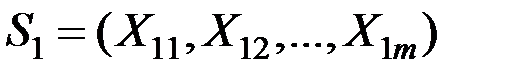и
и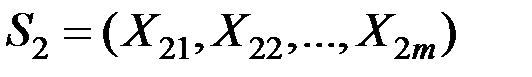 
с математическими ожиданиями
и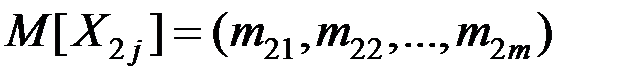 
и одинаковыми ковариационными матрицами
.
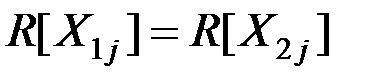Если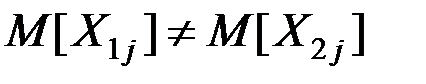 
(т.е. центры совокупностей не совпадают), то выборочное пространство случайных величин 
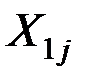и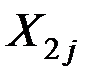 
можно разделить на две област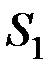и 
и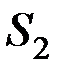 
гиперплоскостью
.
Левая часть уравнения
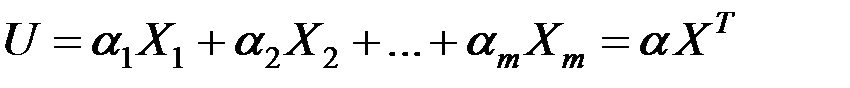
называется дискриминантной функцией.
Здесь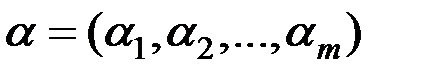 
вектор коэффициентов дискриминантной функции.
Област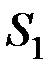и и 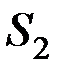можно задать неравенствами
, 
.
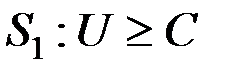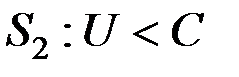Величина С называется пороговым значением.
Пусть имеется элемент выборки (или объект), которому соответствует вектор наблюдений
.
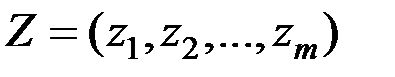Если U(Z) і C, то Z относим к 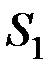, если же U(Z) < C, то Z относим к .
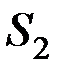Таким образом, задача дискриминации сводится к определению коэффициентов 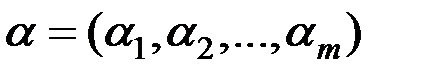дискриминантной функции U и порогового значения С (рис. 6.5).
Рис. 6.5. Графическое представление дискриминантной функции
для двух переменных и двух обучающих выборок
Алгоритмы классификации
1. Рассмотрим случай 
.
Пусть имеются две генеральные совокупности одномерной величины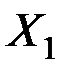 
и 
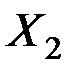с известными законами распределениями 
и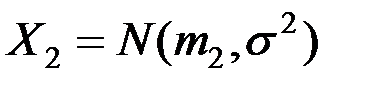 
(рис. 6.6).
Пусть наблюдаемый объект имеет значение Z. К какой из генеральных совокупносте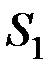й ( или 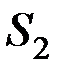) принадлежит этот объект?
Рис. 6.6. Принятие решения для одной переменной
Функция плотность величины 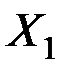при 
равна
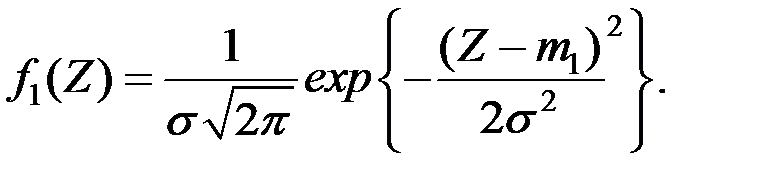
Функция плотность величины 
при 
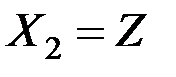равна
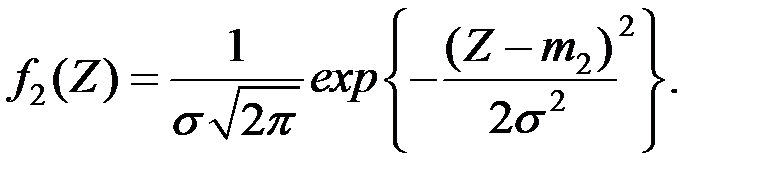
Выбираем следующий простой алгоритм классификации: если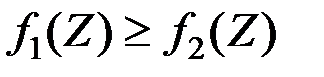 
, то отнесём объект к первой генеральной совокупности 
, если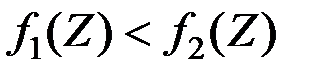 
, то – ко второй совокупности 
.
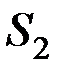Таким образом, имеем правило принятия решения:
; 
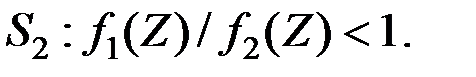
Так как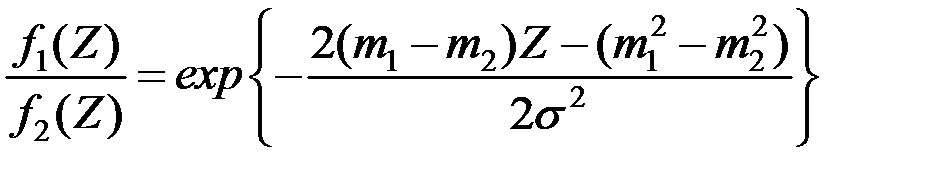 
,
то область задаётся неравенством:
2. Рассмотрим теперь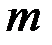 
–мерный случай.
Пусть имеются две генеральные совокупности величин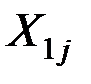 
и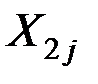 
с известными 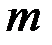–мерными распределениям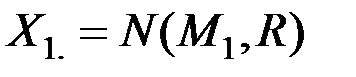и
и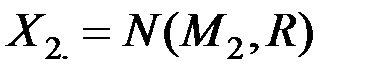 
.
Для вектора наблюдений 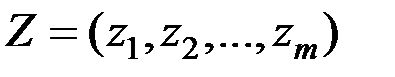плотности вероятностей этих величин равны соответственно
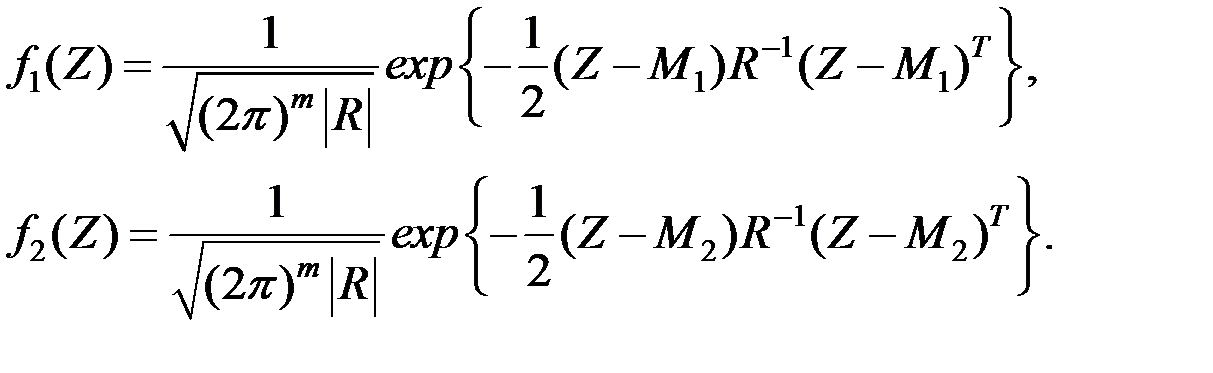
Области и 
определяются аналогично:
; 
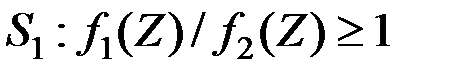Для области получаем обобщение неравенства
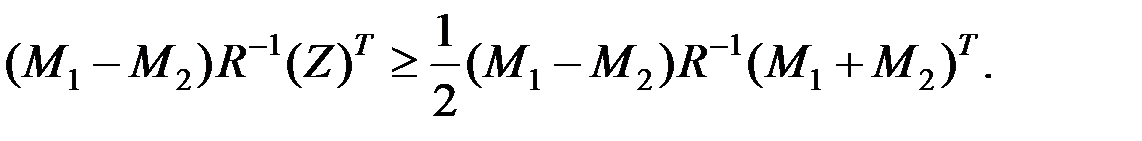
Если обозначить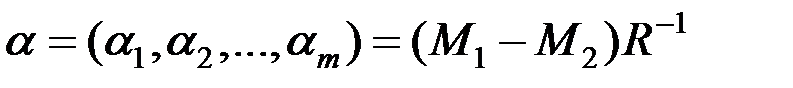 
и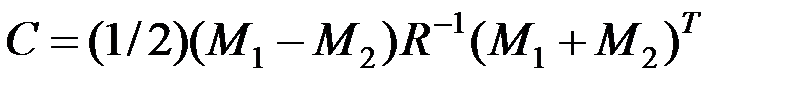 
,
то указанное неравенство можно записать в виде
,
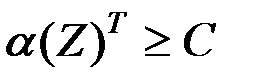где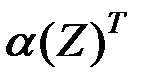 
– дискриминантная функция,
С – пороговое значение.
3. Предположим теперь, что известны априорные вероятност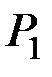и 
и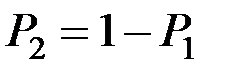 
того, что случайно наблюдаемый объект принадлежит соответственно к первой генеральной совокупности или ко второй.
Пусть также известны стоимости ошибочной классификации:
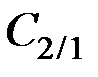– стоимость потерь из–за отнесения ко второй генеральной совокупности вектора наблюдений 
, принадлежащего к первой генеральной совокупности;
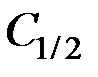– стоимость потерь из–за отнесения к первой генеральной совокупности вектора наблюдений , принадлежащего ко второй генеральной совокупности.
Тогда по теореме Байеса наблюдаемый вектор будет принадлежать первой совокупности 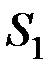с вероятностью
,
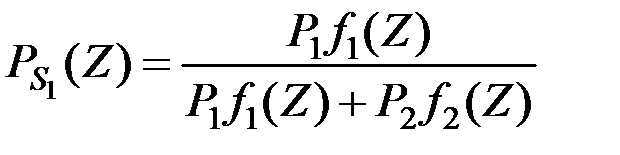а второй совокупности с вероятностью
.
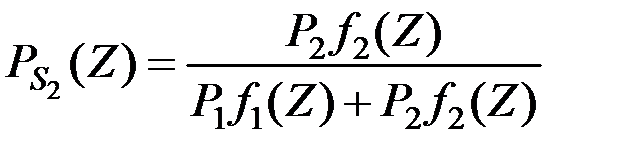Тогда, если мы отнесём вектор наблюдений к первой совокупности 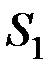, то математическое ожидание потерь составит величину
.
Если отнести вектор наблюдений ко второй совокупности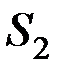 
, то математическое ожидание потерь составит величину
.
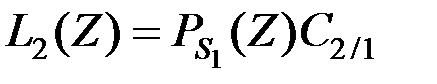В качестве алгоритма классификации примем
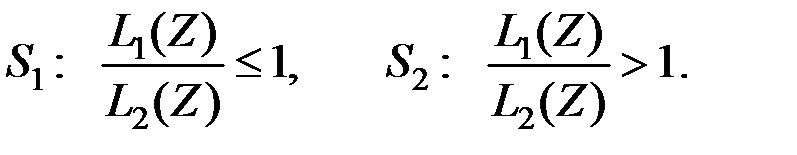
Несложно определить, что область 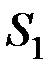задаётся неравенством
.
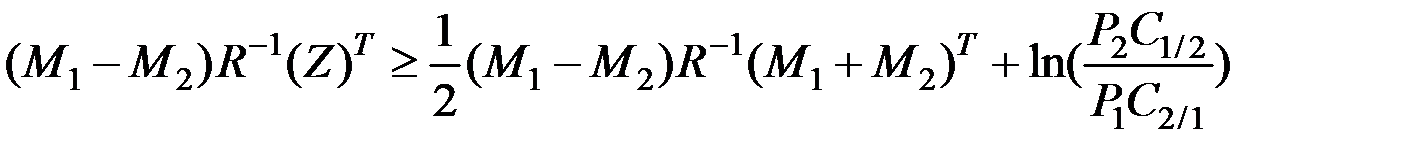Если какая–либо априорная информация о генеральных совокупностях отсутствует, то обычно полагают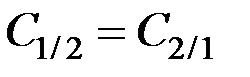 
.
Если 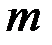–мерные векторы математических ожиданий 
, 
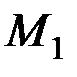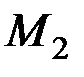и ковариационная матрица R генеральных совокупностей неизвестны, то по обучающим выборкам 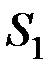и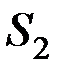 
находят оценки этих параметров. В этом случае оценка ковариационной матрицы вычисляется по формуле
где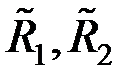 
– несмещённые оценки ковариационных матриц 
;
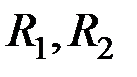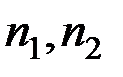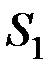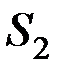– объёмы выборок из и соответственно.
4. Рассмотрим задачу дискриминации для случая G нормально распределённых генеральных совокупностей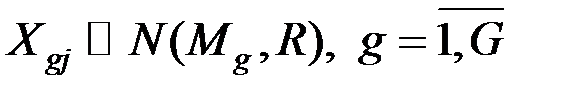 
.
Дискриминантную функцию i –й и q –й совокупностей можно записать в виде
.
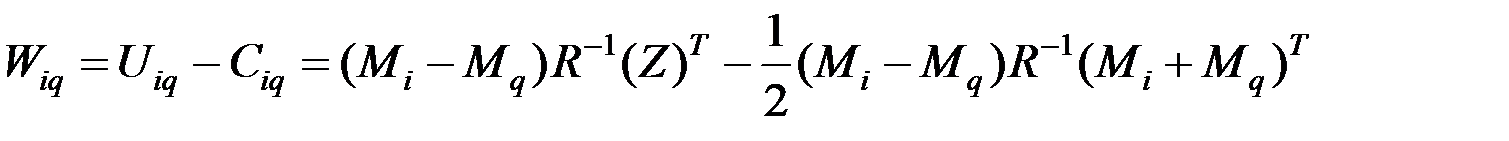Если параметры генеральных совокупностей неизвестны, то вычисляют их оценки по соответствующим обучающим выборкам, причём
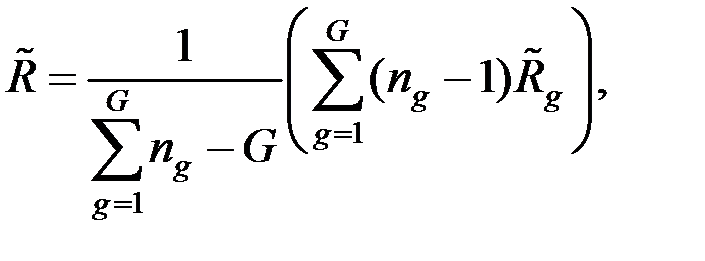
где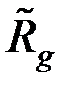 
– несмещённая оценка ковариационной матрицы 
;
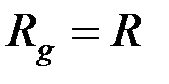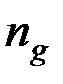– объём выборки из 
–й совокупности, 
.
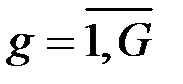Если для всех q № i выполняется неравенство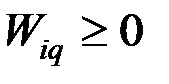 
, то наблюдаемый вектор относят к совокупности 
.
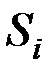Дискриминантный анализ широко используется во многих прикладных исследованиях: психологическое тестирование взрослых и детей; тестирование при приёме на работу; анализ переписи населения; изучение эффектов какого–либо метода лечения; изучение различий между фирмами, географическими районами; социологические исследования и др.
Считается, что наилучшим правилом классификации является байесовское решающее правило, обеспечивающие минимальные средние потери от неправильной классификации и основанные на отношении апостериорных вероятностей различных классов в данной точке пространства признаков.
На практике эти отношения оцениваются по обучающей выборке (наблюдениям с известной классификацией) с помощью параметрических и непараметрических методов. Примером могут служить линейные дискриминантные функции Р.Фишера для нормальных распределений или метод "ближайшего соседа".
Другим возможным методом дискриминантного анализа является минимизация оценки среднего риска или метод "скользящего экзамена" в заранее заданном классе решающих правил.
Линейная дискриминантная функция Р.Фишера – такая линейная комбинация признаков, средние значения которых в разных классах, отнесённые к их средним квадратическим отклонениям максимально различаются.
Для нормальных распределений, отличающихся только средними, дискриминантная функция задаёт байесовское правило классификации.
В дискриминантном анализе нескольких классов для реализации байесовского решающего правила надо рассматривать несколько функций, позволяющие сравнивать апостериорные вероятности классов.
Рассмотрим применение дискриминантного анализа для прогнозирования вероятности банкротства. В результате финансового анализа деятельности фирмы получается система показателей, которая характеризует состояние дел в фирме. Какие–то показатели могут находиться в критической зоне, а какие–то могут быть вполне удовлетворительными.
Задача прогнозирования банкротства может быть решена методом дискриминантного анализа. В этом случае речь идёт о делении всех фирм (предприятий) на две генеральные совокупности:
1) подлежащие банкротству; 2) способные избежать банкротства.
Данная задача решалась американским учёным Э. Альтманом.
За определённый период собирались данные о финансовом положении нескольких фирм (порядка 20) по нескольким показателям (двум, пяти, семи), так или иначе влияющим на возможность банкротства.
В результате наблюдений часть обследуемых фирм оказалась банкротами, а часть выжила. Эти данные послужили обучающими выборками.
В простейшей двухфакторной модели факт банкротства определялся значениями двух показателей:
1) коэффициента покрытия Кп, т.е. отношением текущих активов к краткосрочным обязательствам;
2) коэффициентом финансовой зависимости Кфз, т.е. отношением заёмных средств к общей величине активов.
Первый показатель характеризует ликвидность, второй – финансовую устойчивость фирмы. Очевидно, что при прочих равных условиях вероятность банкротства тем меньше, чем больше Кп и меньше Кфз.
Задача состоит в нахождении уравнения дискриминантной границы
U = a0 + a1Кп + a2Кфз,
которая разделит все возможные сочетания (комбинации) указанных показателей на два класса:
1) значения показателей, при которых фирма обанкротится;
2) значения показателей, при которых фирме банкротство не грозит.
В результате обработки статистических данных было получено уравнение
U = – 0,3877 – 1,0736Кп + 0,0579Кфз.
При U = 0 получаем уравнение дискриминантной границы.
При U > 0 относим фирму к подлежащим банкротству, при U < 0 – к способным избежать банкротства.
Можно также связать значение U с вероятностью предстоящего банкротства. Считаем, что вероятность банкротства возрастает с ростом U, и при U = 0 эта вероятность равна 0,5.
В пятифакторной модели учитывались показатели ликвидности, финансовой устойчивости, рентабельности и активности:
Коб – доля оборотных средств в активах, т.е. (текущие активы)/активы;
Кнп – рентабельность активов, исчисленная по нераспределённой прибыли, т.е. (чистая прибыль – дивиденды)/активы;
Кр – рентабельность активов, исчисленная по балансовой прибыли, т.е. (балансовая прибыль до вычета налогов)/активы;
Кп – коэффициент покрытия по рыночной стоимости собственного капитала, т.е. (рыночная стоимость акций фирмы)/(краткосрочные обязательства);
Кот – отдача всех активов, т.е. (выручка от реализации)/(активы).
Пятифакторная модель имела вид
U = 1,2 Коб + 1,4 Кнп + 3,3 Кр + 0,6 Кп + 1,0 Кот.
В зависимости от значения U можно прогнозировать вероятность банкротства:
если U Ј 1,8 , то вероятность банкротства очень высокая;
если 1,8 < U Ј 2,7, то вероятность банкротства высокая;
если 2,7 < U Ј 2,9, то вероятность банкротства возможная;
если 2,9 < U, то вероятность банкротства очень низкая.
Пример 6.5. Каждое предприятие характеризуется пятью экономическими показателями: Х1 - производительность труда; Х2 - удельный вес рабочих в составе промышленного персонала; Х3 - коэффициент сменности оборудования; Х4 - удельный вес потерь от брака; Х5 - фондоотдача активной части основных производственных фондов. Даны две обучающие выборки, первая из которых включает 9 передовых предприятий (группа 1), а вторая – 8 остальных предприятий (группа 2).
| № предп. | Группа | Х1 | Х2 | Х3 | Х4 | Х5 |
| 1 | 1 | 9,26 | 0,78 | 1,37 | 0,23 | 1,45 |
| 2 | 1 | 9,38 | 0,75 | 1,49 | 0,39 | 1,3 |
| 3 | 1 | 12,11 | 0,68 | 1,44 | 0,43 | 1,37 |
| 4 | 1 | 9,35 | 0,62 | 1,35 | 0,15 | 1,91 |
| 5 | 1 | 9,87 | 0,76 | 1,39 | 0,34 | 1,68 |
| 6 | 1 | 9,12 | 0,71 | 1,27 | 0,09 | 1,89 |
| 7 | 1 | 9,37 | 0,79 | 1,4 | 0,21 | 2,3 |
| 8 | 1 | 10,02 | 0,76 | 1,22 | 0,32 | 2,62 |
| 9 | 1 | 9,42 | 0,7 | 1,2 | 0,28 | 2,03 |
| 10 | 2 | 5,49 | 0,74 | 1,1 | 0,05 | 1,02 |
| 11 | 2 | 6,61 | 0,72 | 1,23 | 0,48 | 0,88 |
| 12 | 2 | 7,37 | 0,77 | 1,38 | 0,62 | 1,09 |
| 13 | 2 | 6,64 | 0,77 | 1,35 | 0,5 | 1,32 |
| 14 | 2 | 5,52 | 0,72 | 1,24 | 1,2 | 0,68 |
| 15 | 2 | 5,68 | 0,71 | 1,28 | 0,66 | 1,43 |
| 16 | 2 | 5,22 | 0,79 | 1,33 | 0,74 | 1,82 |
| 17 | 2 | 6,7 | 0,79 | 1,35 | 0,39 | 1,24 |
Подлежат дискриминации (классификации) предприятия № 18, 19:
| № предп. | Группа | Х1 | Х2 | Х3 | Х4 | Х5 |
| 18 | ? | 8,17 | 0,73 | 1,16 | 0,38 | 1,94 |
| 19 | ? | 6,5 | 0,66 | 1,15 | 0,29 | 1,85 |
По обучающим выборкам построить дискриминантную функцию и провести классификацию объектов № 18, 19.
Решение.
Задача состоит в том, чтобы найти уравнение дискриминантной границы, которая разделит все возможные комбинации указанных показателей на две группы:
1) значения показателей, при которых предприятие следует отнести к группе передовых;
2) значения показателей, при которых предприятие следует отнести к группе остальных (непередовых) предприятий.
Проведём дискриминантный анализ с помощью пакета программ SPSS 12.0 (Анализ – Классифицировать – Дискриминантный анализ).
В окне просмотра SPSS приводится таблица, содержащая средние значения, стандартные отклонения, количество наблюдений для каждой группы в отдельности и суммарные показатели для обеих групп.
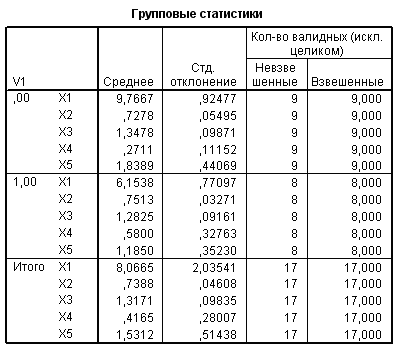
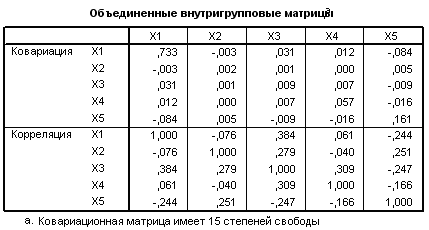
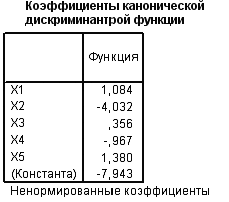
В SPSS сохраняется таблица, в которой построчно для каждого наблюдения приводится информация о принадлежности к одной из двух групп и значении дискриминантной функции.
В последней колонке содержится информация о прогнозной вероятности принадлежности объекта к первой группе, сделанной на основании значения дискриминантной функции:
| № предприятия | Предсказанная группа | Значения дискриминантной функции | Вероятность принадлежности к группе 0 |
| 1 | 0 | 1,21493 | 0,99923 |
| 2 | 0 | 1,147 | 0,9989 |
| 3 | 0 | 4,42871 | 1 |
| 4 | 0 | 2,66249 | 1 |
| 5 | 0 | 2,17486 | 0,99999 |
| 6 | 0 | 2,05224 | 0,99999 |
| 7 | 0 | 2,49647 | 1 |
| 8 | 0 | 3,59312 | 1 |
| 9 | 0 | 2,40228 | 1 |
| 10 | 1 | – 3,22567 | 0 |
| 11 | 1 | – 2,49366 | 0 |
| 12 | 1 | – 1,66375 | 0,00037 |
| 13 | 1 | – 2,03241 | 0,00005 |
| 14 | 1 | – 4,64383 | 0 |
| 15 | 1 | – 2,85899 | 0 |
| 16 | 1 | – 3,20177 | 0 |
| 17 | 1 | – 2,052 | 0,00005 |
| 18 | 0 | 0,69121 | 0,98816 |
| 19 | 1 | – 0,87752 | 0,02214 |
Кластерный анализ
Рассматривается некоторая выборка наблюдаемых показателей
.
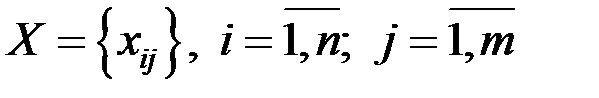Задача состоит в классификации элементов выборки (объектов) по группам (классам, кластерам, таксонам, множествам) так, чтобы объекты внутри групп были схожими ("близкими" по соответствующим характеристикам), а сами группы были бы максимально различными (разделёнными), насколько это возможно.
Критерием классификации является некоторая функция "близости" или расстояние между объектами.
Например, при классификации показателей характеристикой расстояния между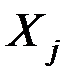 
и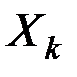 
часто является коэффициент корреляции 
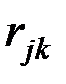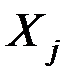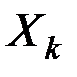, т.е. в этом случае функция "близости" или "расстояние" между и может быть задана в виде:
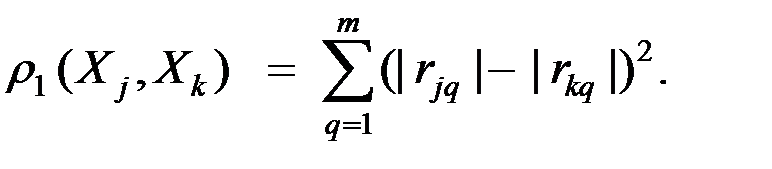
Другими примерами метрик близости являются:
евклидово расстояние между показателями
;
расстояние между объектами
,
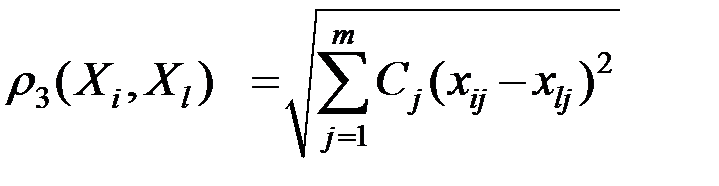где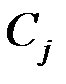 
– вес j–го показателя.
Расстояние Хемминга между показателями имеет вид:
При конструировании различных кластер–процедур часто используется понятие расстояния не между отдельными объектами, а между целыми группами (классами, таксонами) объектов.
1. Расстояние между двумя группами Si и Sj равно расстоянию между ближайшими объектами этих групп ("ближайший сосед"):
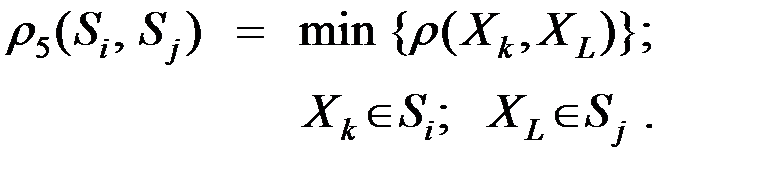
2. Расстояние между двумя группам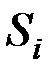и 
и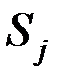 
равно расстоянию между их математическими ожиданиями ("центр тяжести")
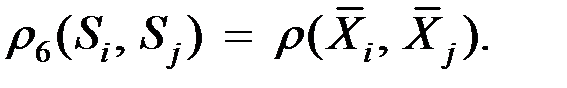
Здесь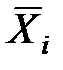 
– вектор математического ожидания для i–й группы.
3. Расстояние между двумя группам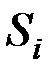и и 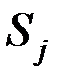равно расстоянию между самыми дальними объектами этих групп ("дальний сосед")
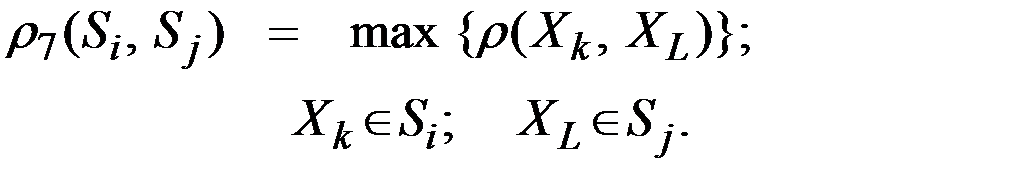
4. Расстояние между двумя группам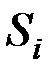и и 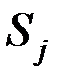равно среднему арифметическому возможных попарных расстояний между представителями рассматриваемых групп:
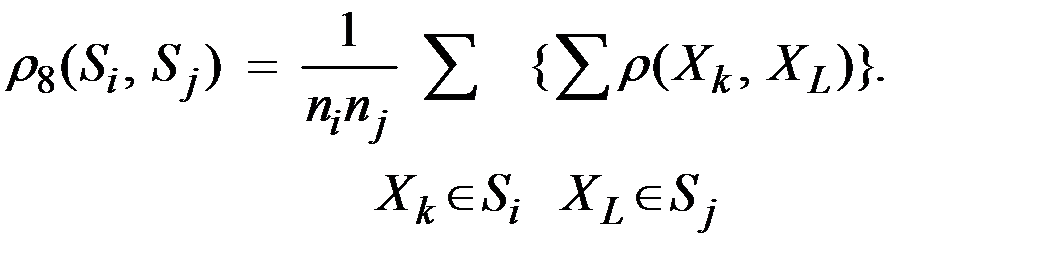
Здесь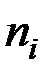 
– число объектов в группе .
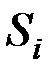На практике иногда целесообразно использовать иерархические кластер–процедуры.
Иерархическая кластер–процедура – это пошаговый алгоритм, при котором на каждом шаге происходит разбиение (объединение) множества объектов, подлежащих классификации, на (в) непересекающиеся кластеры, при этом каждое последующее разбиение (объединение) относится к кластерам, полученным на предыдущем шаге.
При работе таких процедур происходит построение так называемого иерархического классификационного дерева.
Под ним понимается множество разбиений исходной выборки на классы, упорядоченные по уровням иерархии, т.е. по номеру шага иерархической процедуры.
Из сказанного следует существование двух типов процедур:
а) агломеративные, которые на каждом шаге объединяют полученные ранее кластеры в более крупные группы;
б) дивизимные, которые на каждом шаге дробят полученные ранее кластеры на более мелкие.
Примером агломеративной процедуры является пороговый алгоритм.
Здесь имеется монотонно возрастающая последовательность порогов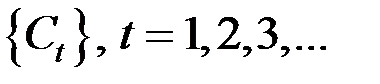 
и на каждом шаге t к одному классу относятся те объекты, расстояние между которыми не превосходит 
.
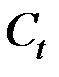К недостаткам иерархических процедур относят громоздкость их реализации на ЭВМ.
Достоинство – делают полный и достаточно тонкий анализ структуры объектов, например, при выявлении естественных групп признаков по алгоритму типа "средней связи" или "ближайшего соседа".
Обнаружив такие группы можно снизить размерность описания либо выбрасыванием дублирующих (близких) признаков, либо заменив каждую группу новым показателем, общим для этой группы свойством с соответствующей интерпретацией.
Общая схема иерархической процедуры (для определённости агломеративной):
1) все объекты считаются отдельными кластерами;
2) два самых близких кластера по матрице межклассовых расстояний объединяются в один;
3) пересчитывается матрица межклассовых расстояний;
4) переход к пункту 2.
Очевидно такая процедура за n – 1 шагов (n – число объектов) объединит все объекты в один кластер.
На каждом шаге будем фиксировать расстояние между объединяемыми кластерами как функцию j(t) от номера шага t.
Такая функция будет монотонно возрастать, поскольку каждый раз происходит объединение ближайших классов, расстояние между которыми наименьшее (рис. 6.7).
Рис. 6.7. Принятие решения о классификации объектов
По производной j '(t) можно принять решение о том, что на (k – 1)–м шаге была самая удачная группировка объектов, т.к. на шаге k были объединены кластеры (объекты) с большим межклассовым расстоянием.
Дендограмма – графическое изображение результатов кластерного анализа в виде дерева решений.
Пример 6.6. Предприятия оцениваются по 6 показателям.
Известна матрица значений показателей по 12 предприятиям:
| № объекта | Х1 | X2 | X3 | X4 | X5 | X6 |
| 1 | 9,26 | 1,37 | 26006 | 167,69 | 47750 | 17,72 |
| 2 | 9,38 | 1,49 | 23935 | 186,1 | 50391 | 18,39 |
| 3 | 12,11 | 1,44 | 22589 | 220,45 | 43149 | 26,46 |
| 4 | 10,81 | 1,42 | 21220 | 169,3 | 41089 | 22,37 |
| 5 | 9,35 | 1,35 | 7394 | 39,53 | 14257 | 28,13 |
| 6 | 9,87 | 1,39 | 11586 | 40,41 | 22661 | 17,55 |
| 7 | 8,17 | 1,16 | 26609 | 102,96 | 52509 | 21,92 |
| 8 | 9,12 | 1,27 | 7801 | 37,02 | 14903 | 19,52 |
| 9 | 5,88 | 1,16 | 11587 | 45,74 | 25587 | 23,99 |
| 10 | 6,3 | 1,25 | 9475 | 40,07 | 16821 | 21,76 |
| 11 | 6,22 | 1,13 | 10811 | 45,44 | 19459 | 25,68 |
| 12 | 5,49 | 1,1 | 6371 | 41,08 | 12973 | 18,13 |
Здесь: X 1 - производительность труда; X2 - коэффициент сменности оборудования; X3 - среднегодовая численность производственного персонала; X4 - среднегодовая стоимость фондов; X5 - среднегодовой фонд заработной платы производственного персонала; X6 - непроизводственные расходы.
Классифицировать предприятия (объекты) по группам (кластерам).
Решение.
Используем агломеративный алгоритм кластеризации.
Расстояние между кластерами определим по правилу «ближайшего соседа». В качестве метрики будем использовать обычное евклидово расстояние.
Так как признаки Х1, X2, X3, X4, X5 , X6 измерены в разных единицах, то перейдём от исходной матрицы данных к стандартизированной матрице:
Стандартизированная матрица данных будет иметь вид:
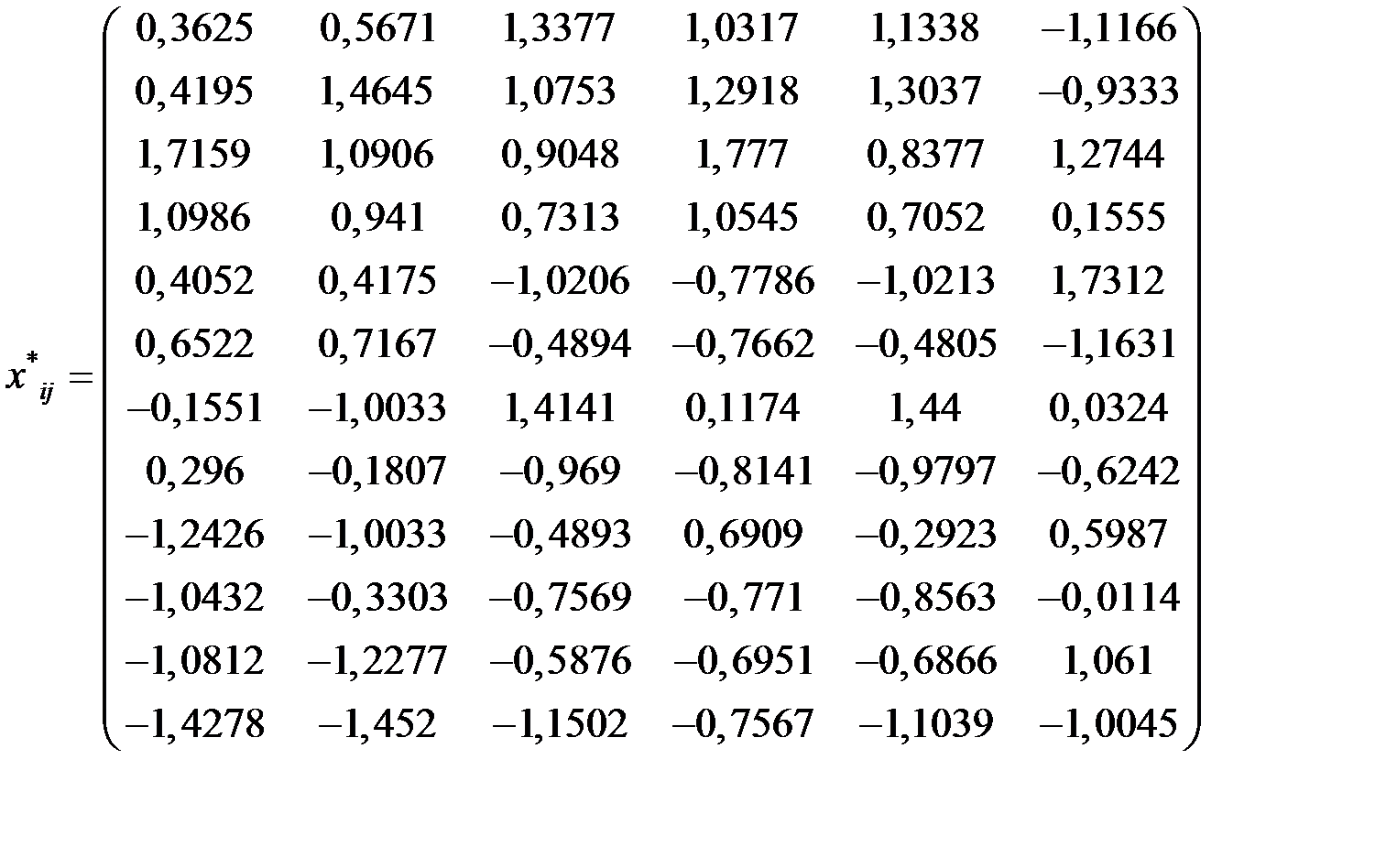
Расстояние между кластерами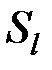 
и 
определяется по формуле:
.
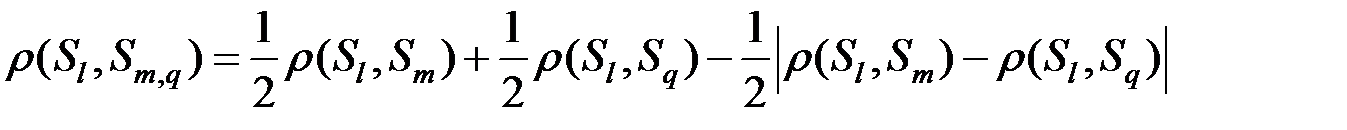Так как число кластеров заранее не задано, то оптимальным (рациональным) считается число кластеров, равное разности количества наблюдений и количества шагов, после которого метрика расстояния увеличивается скачкообразно.
В этом случае процесс объединения в новые кластеры необходимо остановить, так как в противном случае были бы объединены уже кластеры, находящиеся на относительно большом расстоянии друг от друга.
Проведём кластерный анализ с помощью пакета программ SPSS 12.0 (Анализ – Классифицировать – Иерархический кластер – Кластер по наблюдениям; Кластерный метод – «ближайший сосед»; Интервал – евклидово расстояние; Преобразовать значения – стандартизировать).
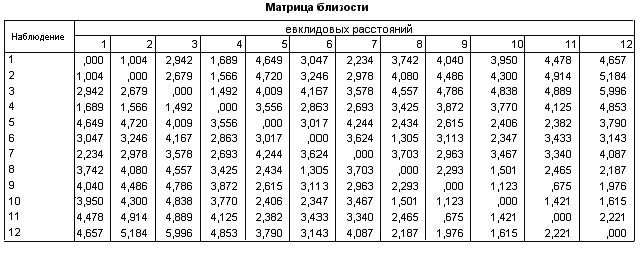
SPSS выдаёт симметричную матрицу расстояний между рассматриваемыми объектами, значения показателей которых подверглись стандартизации.
Ниже приведены оригинальные таблицы и графики результатов работы статистической программы кластерного анализа.
| 
|
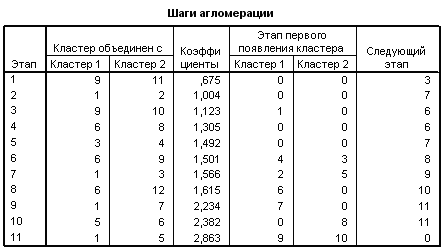
Дендрограмма визуализирует процесс слияния, приведённый в обзорной таблице шагов агломерации. Она идентифицирует объединённые кластеры и значения евклидовых расстояний на каждом шаге (рис. 6.8).
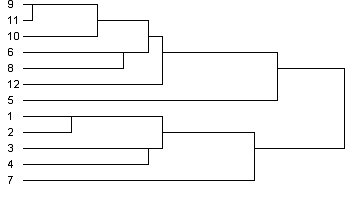
Рис. 6.8. Дендрограмма иерархической кластеризации объектов
Применение агломеративного алгоритма к нестандартизированным данным даёт в данном случае аналогичные результаты классификации объектов (рис. 6.9).
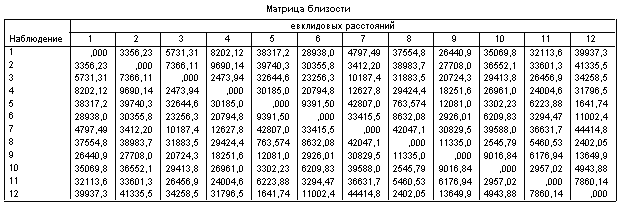
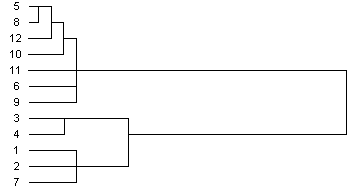
Рис. 6.9. Дендрограмма работы агломеративного алгоритма
с использованием нестандартизированных данных
Таким образом, получили, что предприятия № 1,2,3,4,7 относятся к первому кластеру, а предприятия № 4,6,8,9,10,11,12 – ко второму.
Распознавание образов
Имеется матрица наблюдений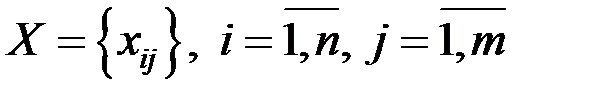 
.
Пусть исследователем указана принадлежность N1 объектов к G образам, множествам, группам, классам, таксонам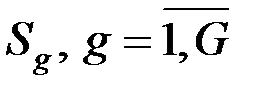 
.
Число объектов, принадлежащих группе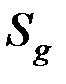 
, известно и равно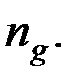 
При этом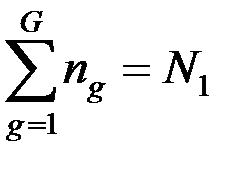 
.
Требуется найти принадлежность остальных N2 = n – N1 объектов к одному из указанных образов.
Множества 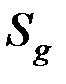обычно называют обучающими выборками (ОВ), объекты не входящие в ОВ – распознаваемыми или классифицируемыми, а сама задача в указанной постановке – задачей распознавания образов.
Существует большое число различных способов решения указанной задачи в зависимости от дополнительных свойств всего множества n объектов или его отдельных частей.
1. Байесовская теория принятия решения основана на минимизации общего риска принятия решения.
Предполагается, что известна статистическая структура обучающих выборок, то есть вид распределения случайных величин, соответствующих каждому из образов.
Если вид распределения неизвестен, то находят его оценку или вероятность появления объектов в каждой точке пространства.
Пусть f(x|Sg), xОRm – oценка функции плотности распределения (ОФПР) для образа Sg.
При условии равновероятного появления образов Sg объект с координатами x* следует отнести к тому образу, для которого f(x*|Sg) максимальнa.
При различных вероятностях образов P(Sg) каждая из ОФПР домножается на некоторый коэффициент, зависящий от P(Sg).
2. Локальные методы распознавания учитывают расположение ближайших к х* точек ОВ и опираются на оценку
f(x*|Sg) = Mg/(ngV),
где V – объём некоторой окрестности точки;
Mg – число объектов образа Sg, попавшего в этот объём.
Например:
а) правило "ближайшего соседа" – классифицируемый объект относится к тому образу, которому принадлежит ближайший объект из ОВ;
б) "средняя связь" – объект относится к той ОВ (образу), сумма расстояний до объектов которой меньше всего;
в) "дальний сосед" – объект относится к ОВ, расстояние до самого далекого объекта которой минимально.
3. Рекурсивный алгоритм распознавания образов базируется на рекурсивном отображении многомерного пространства на числовую ось.
Рекурсивное отображение многомерного пространства на числовую ось заключается в следующем.
Имеем матрицу стандартизованных наблюдений
.
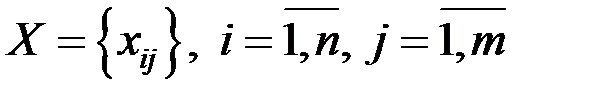Пусть Dm – единичный m – мерный гиперкуб, тогда D1 – единичный интервал.
Гиперкуб разобьём на 2m гиперкубов, называемых квантами первого разбиения. Длина ребра такого кванта равна 1/2.
Кванты нумеруются индексом i1 от 0 до 2m – 1 так, чтобы номера квантов, имеющих общую грань, отличались на единицу.
Обозначаются кванты первого разбиения – d(i1), i1 = 0,1,...,2m – 1.
Каждый квант первого разбиения аналогично разбивается на кванты второго разбиения с длиной ребра 1/4, которые нумеруют по тому же закону, что и кванты первого разбиения.
При этом нулевой квант второго разбиения, входящий в d(i1), должен иметь общую грань с (2m – 1) – м квантом второго разбиения, входящим в d(i1 –1).
Кванты второго разбиения обозначим d(i2), где i2 – номер кванта второго разбиения, входящего в квант d(i1) (рис. 6.10).
| 1 | 2 | 1 | 2 |
| 0 | 3 | 0 | 3 |
| 3 | 2 | 1 | 0 |
| 0 | 1 | 2 | 3 |
Рис. 6.10. Нумерация квантов второго разбиения
Аналогично получаем кванты любого разбиения с номером k.
Гиперкуб Dm, рекурсивно квантованный k раз, называется дискретным пространством k–го разбиения и обозначается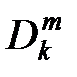 
.
В частности при m = 1 получаем k раз квантованный единичный интервал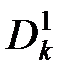 
.
Если в каждом разбиении число частей, на которые делится квант предыдущего разбиения из 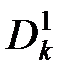, выбрать равным 2m, то при любом k количество квантов в 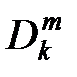и 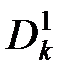совпадают, и каждое из них равно 2m k.
Кванты k – го разбиения пространства 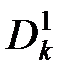, полученные из одного кванта (k – 1) – го разбиения нумеруются слева направо индексом i k, i k = 0, 1, ..., 2m – 1 и обозначаются q(i1, i2, ..., i k).
Сопоставив кванты d и q с одинаковыми наборами индексов (i1, i2, ..., i k) получим взаимно однозначное отображение
j к: 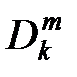Ю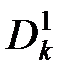
или для отдельных квантов:
j k: [d(i1, i2, ..., ik)] = q(i1, i2, ..., i к).
Если для каждого конкретного номера разбиения k считать все точки, входящие в один квант k–го разбиения, неразличимыми, то образом произвольной точки xОDm при отображении j к можно считать любую точку кванта
q(i1, i2, ..., ik) = j k [d(i1, i2, ..., ik)]
при условии
x Оd(i1, i2, ..., i k).
Для определённости всем точкам кванта приписываются координаты его центра, поэтому j k (х) есть координаты центра кванта q(i1, i2, ..., iк) и, наоборот, каждой точке у ОD1 ставится в соответствие точка j –1k (у) – центр кванта
d(i1, i2, ..., i k)О .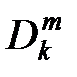
Впишем исходные данные для обучающих выборок в дискретное пространство размерности m с номером разбиения k, пронормировав предварительно значения каждого показателя с учётом допустимых преобразований данной шкалы к интервалу [0,1).
Используя рекурсивное отображение
j k: 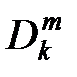Ю ,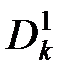
построим на единичном полуинтервале [0,1) образы всех объектов из ОВ.
Общий подход к построению решающего правила состоит в разбиении 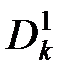на системы отрезков
{Si1}, {Si2}, ..., {SiG}, (i = 1, 2, ...., ig)
в соответствии с расположением в 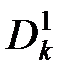объектов ОВ, так чтобы
.
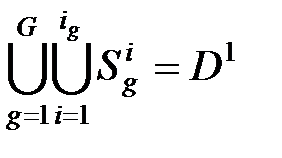Тогда для принятия решения о принадлежности распознаваемого объекта достаточно отобразить этот объект в 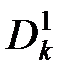и определить, в какую систему отрезков {Si k} входит этот образ.
Пусть ОВ для первого класса есть выборка из генеральной совокупности с плотностью f(x), xОDm.
Оценим значение плотности в произвольной точке xО 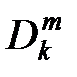, используя координаты образов объектов ОВ в .
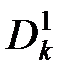В качестве оценки f(x) возьмём величину частоты попадания объектов ОВ в некоторую окрестность VО 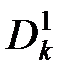точки
y = j k (х): f(y|Si1) = М1/(n1L),
где М1 – число объектов первого класса, попавших в V;
L – длина окрестности V, L = mes(V);
n1 – общее число объектов первого класса в ОВ.
Предлагаемая оценка сходится к f(x) при n1 Ю Ґ.
Аналогичным образом могут быть получены оценки плотностей распределения и для остальных распознаваемых классов.
В этом случае решающее правило в D1 определяется множеством точек yОD1, в которых выполняется условие равенства функций плотности распределения различных классов.
В Dm этому множеству соответствует гиперповерхность, разделяющая классы.
Она оптимальна в отношении минимума ошибки классификации, т.к. является множеством точек, в которых выполняется условие равенства многомерных функций плотности распределения.
Таким образом, решающее правило состоит в приписывании распознаваемому объекту номера того класса, образов объектов ОВ которого больше всего на отрезке длины L, т.к. при любой длине окрестности L приведённая выше оценка пропорциональна числу объектов данного класса.
С учётом того что ОФПР неразличима для точек y, принадлежащих одному кванту k–го разбиения, решающее правило в D1 определяется уже не множеством точек, а объединением множества квантов k–го разбиения, в которых совпадают ОФПР различных классов, и множества границ квантов, на которых происходит изменение отношения "больше–меньше" между оценками.
В Dm этому объединению будет соответствовать некоторая область, являющаяся аппроксимацией разделяющей гиперповерхности, причём уровень дробления пространства даёт различную точность аппроксимации этой гиперповерхности.
Окончательно получаем следующее правило: классифицируемый объект, попавший в квант i k, приписывается к тому классу, объектов ОВ которого больше в этом кванте данного разбиения.
Решение об окончательной классификации принимается по совокупности всех локальных решений (на каждом уровне разбиения).
Если решение о классификации для некоторого объекта не может быть принято на уровне (шаге) разбиения k, то рассматривается возможность принятия решения на уровне k – 1 и т.д., до тех пор, пока объект не будет приписан к одному из возможных классов.
Если ни на одном разбиении классификация объекта не может быть осуществлена, то решение принимается по ближайшему на интервале [0,1) объекту из ОВ (рис. 6.11).
Рис. 6.11. Принятие решения о классификации на интервале [0,1)
Дата: 2019-03-05, просмотров: 794.
