При использовании построенной модели для прогнозирования делается предположение о сохранении в период прогнозирования существовавших ранее взаимосвязей переменных. Для прогнозирования зависимой переменной на τ шагов вперёд необходимо знать прогнозные значения всех входящих в неё факторов 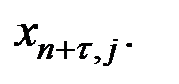
Их оценки могут быть получены на основе экстраполяционных моделей или заданы пользователем (экспертно). Эти оценки подставляются в модель и получаются прогнозные оценки.
Для линейной модели множественной регрессии доверительный интервал рассчитывается следующим образом:
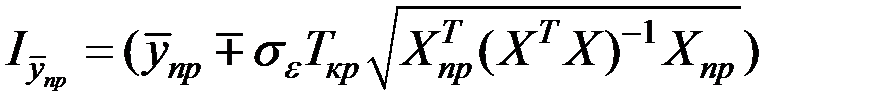 .
.
Здесь
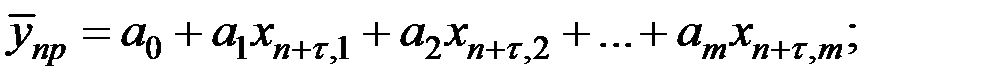
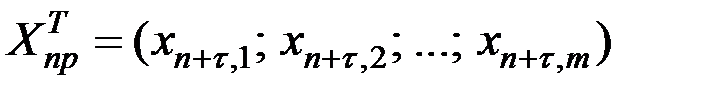 .
.
Пример 5.6. Имеются 10 наблюдений за тремя показателями 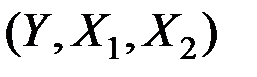 :
:
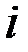
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
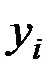
| 11 | 21 | 22 | 15 | 10 | 12 | 13 | 9 | 12 | 16 |
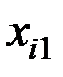
| 15 | 20 | 23 | 18 | 16 | 17 | 18 | 19 | 16 | 24 |
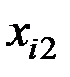
| 6 | 9 | 10 | 7 | 8 | 9 | 7 | 5 | 6 | 8 |
Получить и исследовать уравнение линейной множественной регрессии.
Решение. Вычислим числовые характеристики исследуемых показателей:
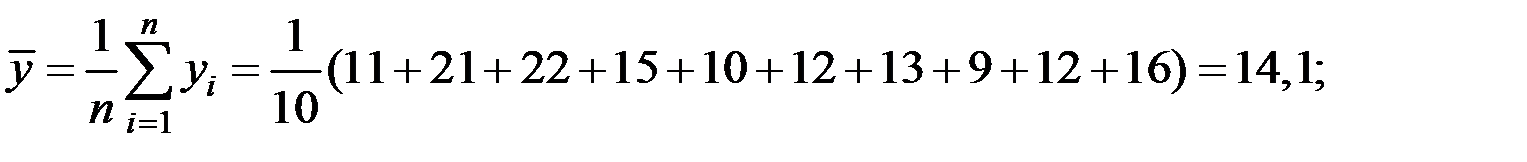
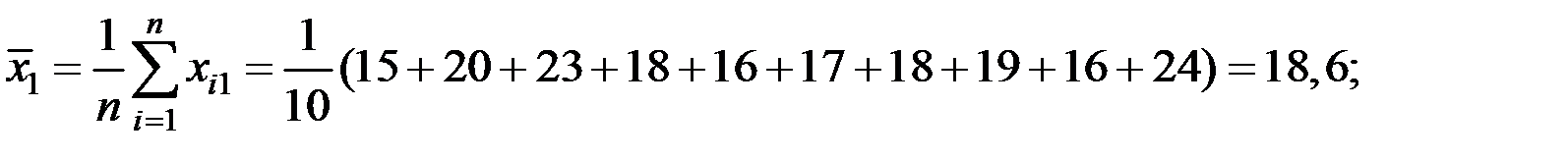
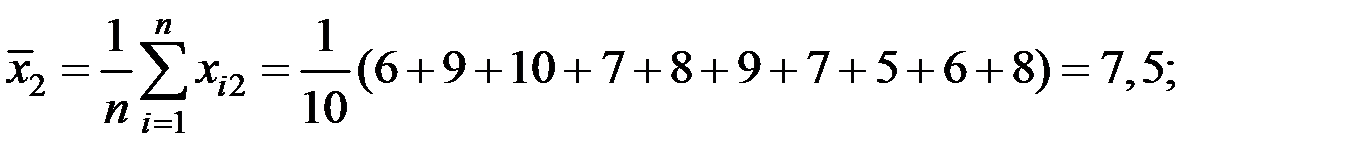
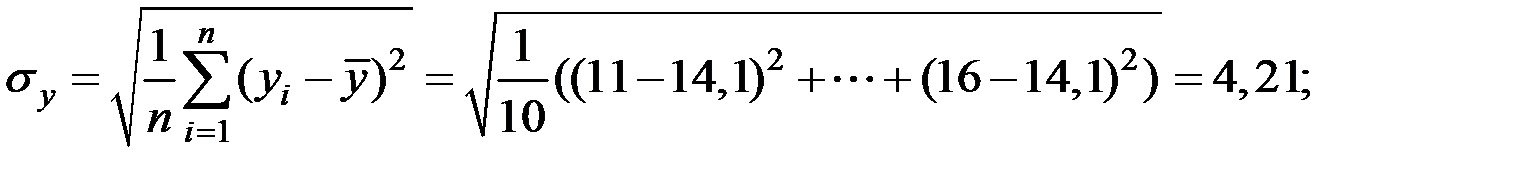
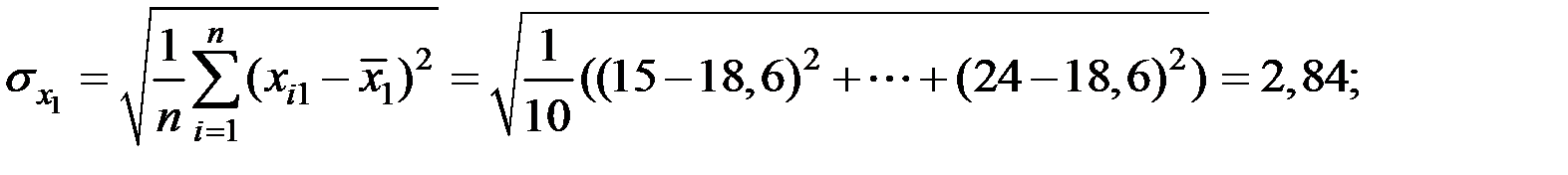
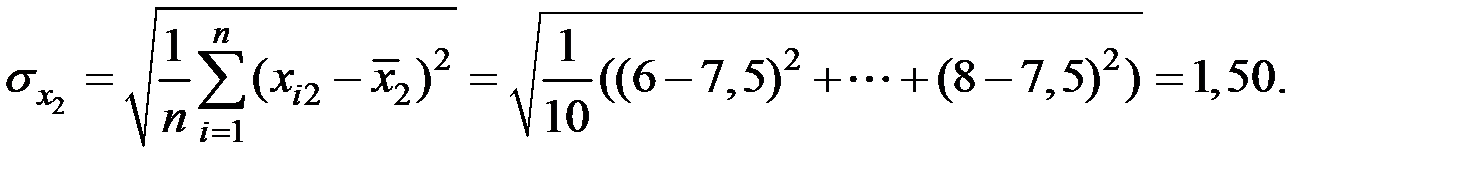
Вычислим параметры модели регрессии в матричном виде.
Имеем матрицы:
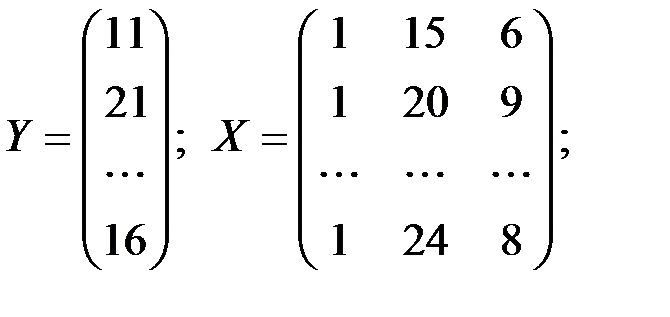
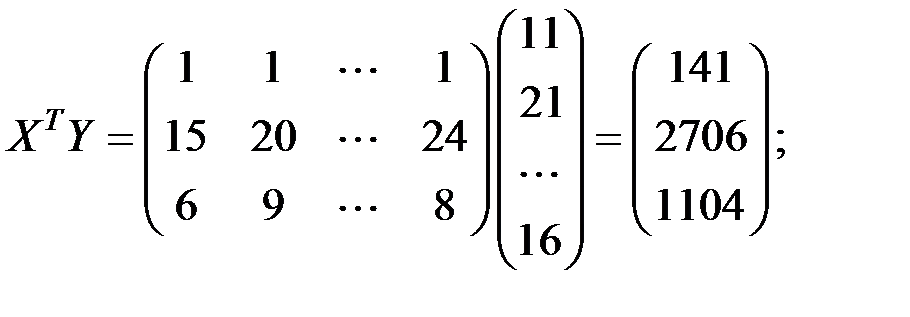
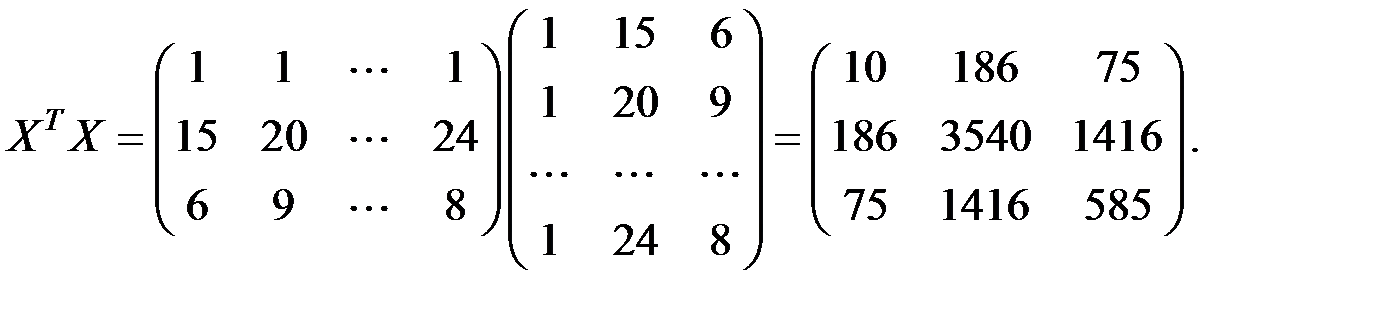
Обратную матрицу 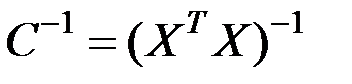 определим по формуле
определим по формуле
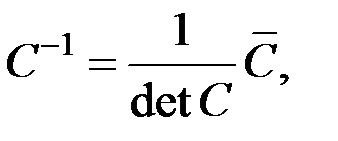
где 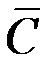 − матрица алгебраических дополнений элементов
− матрица алгебраических дополнений элементов 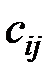 матрицы
матрицы 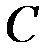
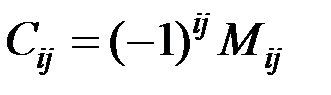 ,
,
где 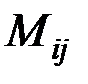 − минор элемента
− минор элемента 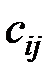 , т.е. определитель порядка
, т.е. определитель порядка 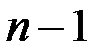 , полученный из матрицы
, полученный из матрицы 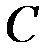 вычёркиванием
вычёркиванием  –ой строки и
–ой строки и  –го столбца.
–го столбца.
Получим: 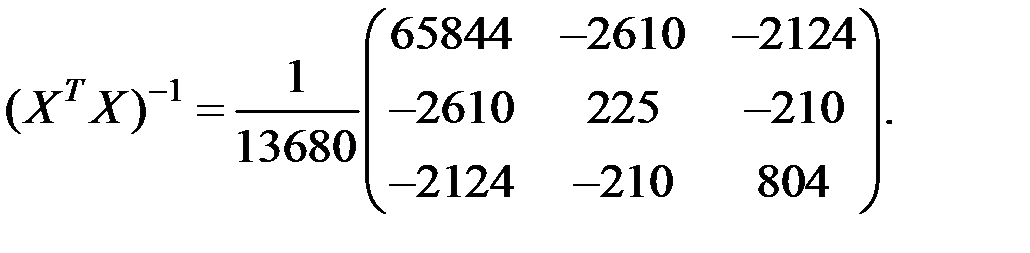
Тогда
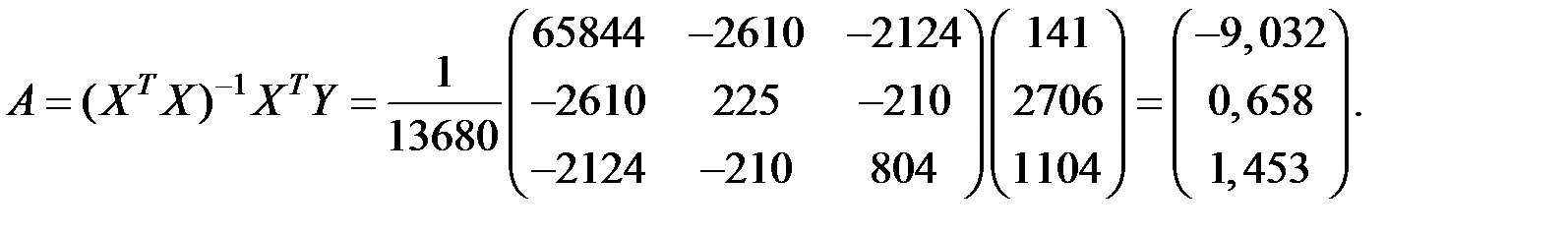
Уравнение множественной регрессии имеет вид:
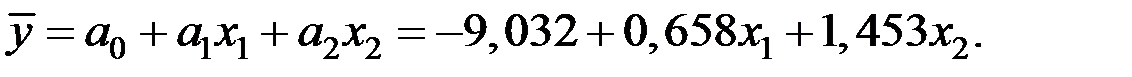
Для сравнения влияния каждой независимой переменной 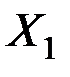 и
и 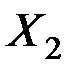 на
на 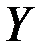 вычислим коэффициенты эластичности.
вычислим коэффициенты эластичности.
Коэффициенты эластичности составят величины:
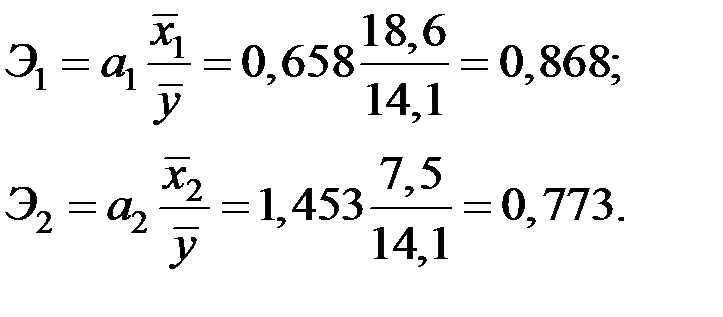
Увеличение переменных 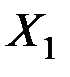 и
и 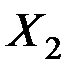 на 1% от своих средних значений приводит в среднем к увеличению
на 1% от своих средних значений приводит в среднем к увеличению 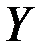 соответственно на 0,868% и 0,773%.
соответственно на 0,868% и 0,773%.
Для сравнения влияния переменных 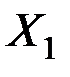 и
и 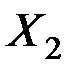 на
на 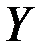 вычислим стандартизированные коэффициенты регрессии:
вычислим стандартизированные коэффициенты регрессии:
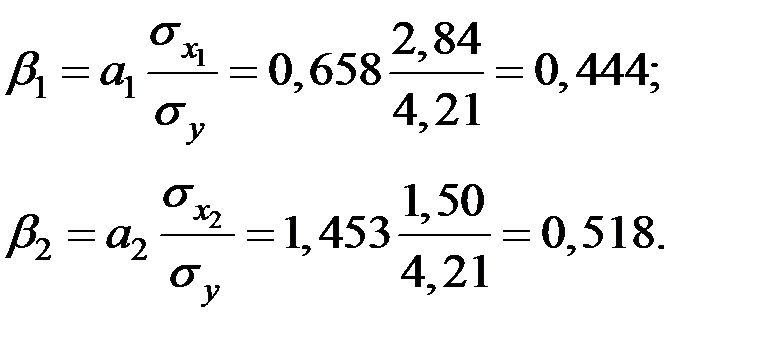
Увеличение показателя 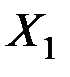 только на одно значение
только на одно значение 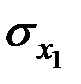 увеличивает в среднем показатель
увеличивает в среднем показатель 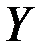 на
на 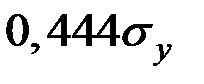 .
.
Аналогично, увеличение 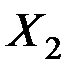 на значение
на значение 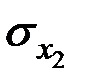 увеличивает
увеличивает 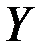 на
на 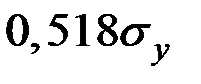 .
.
Долю влияния фактора в суммарном влиянии всех факторов оценим по величине дельта–коэффициентов ( 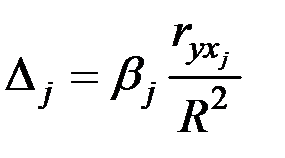 ):
):
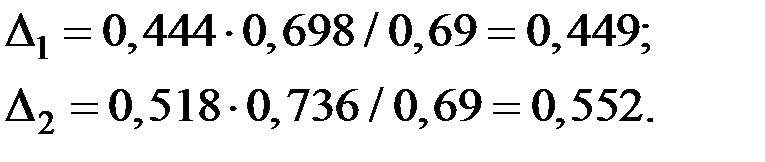
Проверим значимость модели множественной регрессии по 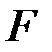 − критерию.
− критерию. 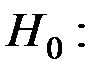 уравнение не значимо.
уравнение не значимо.
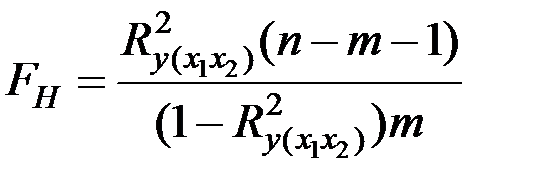 ,
,
где 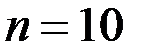 − количество наблюдений,
− количество наблюдений,
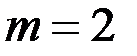 − количество показателей.
− количество показателей.
Вычислим коэффициент детерминации модели по соотношению:
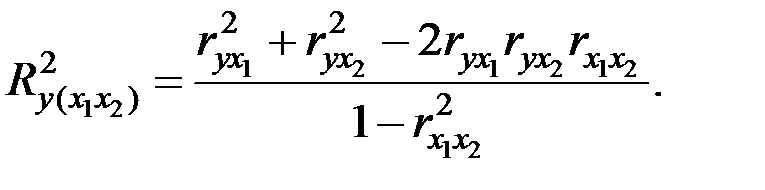
Парные коэффициенты корреляции при этом имеют следующие значения:
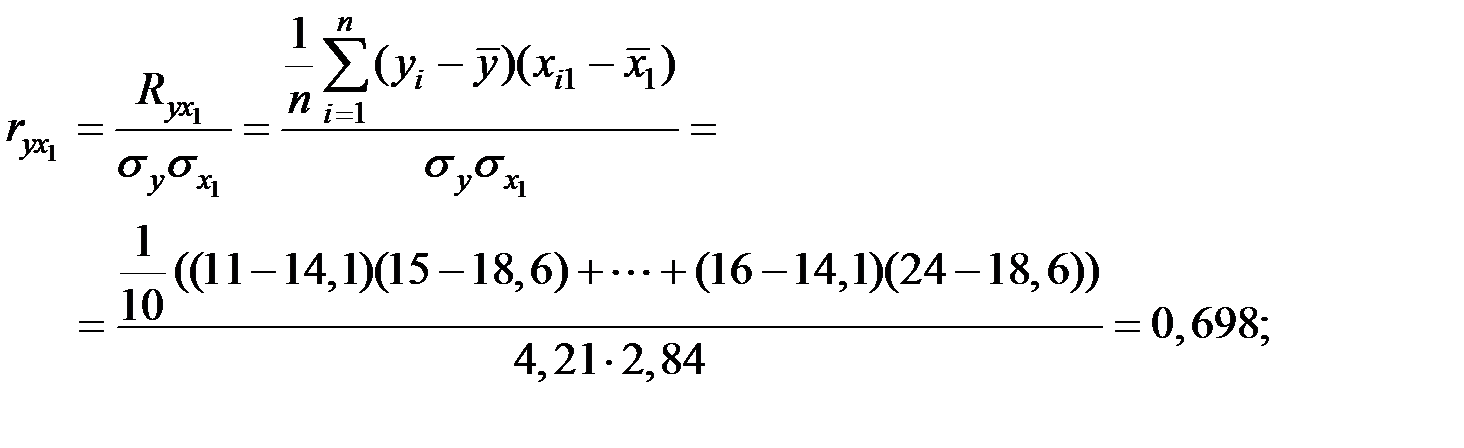
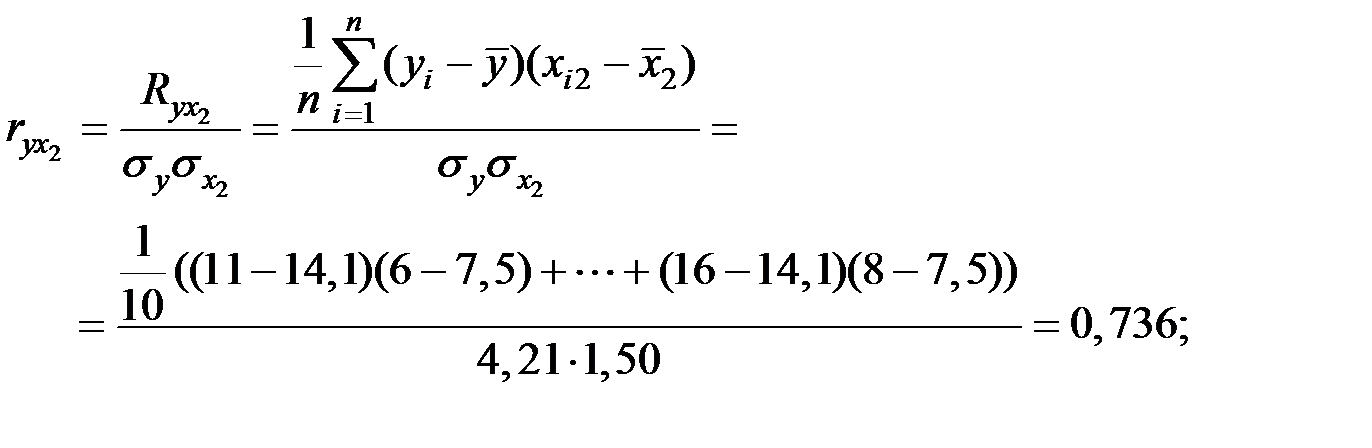
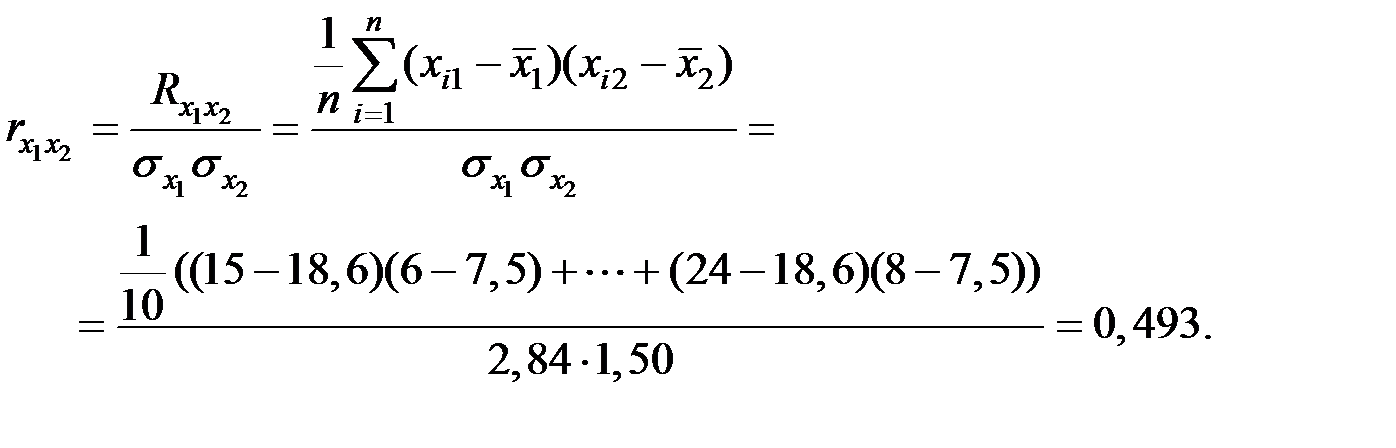
Тогда получаем:
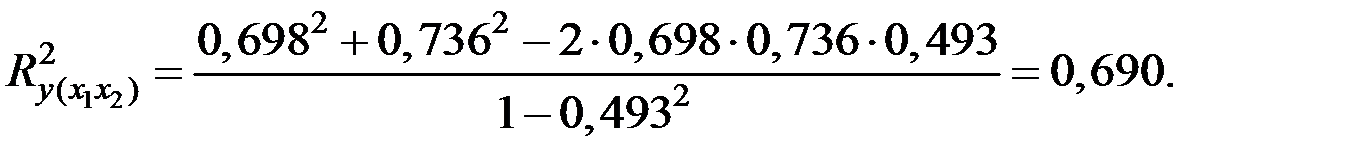
Вычислим наблюдаемое значение критерия.
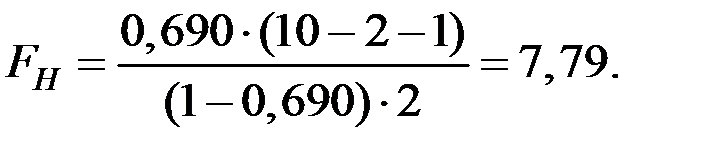
По таблице 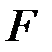 − распределения найдём критическую точку
− распределения найдём критическую точку
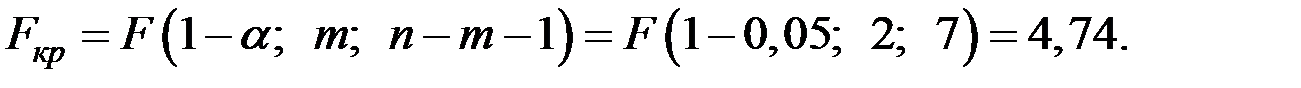
Так как 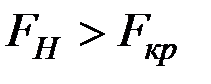 , то есть все основания отвергнуть гипотезу
, то есть все основания отвергнуть гипотезу 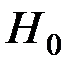 , т.е. модель множественной регрессии значима при уровне значимости
, т.е. модель множественной регрессии значима при уровне значимости 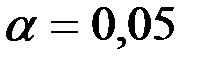 .
.
Проверим на значимость коэффициенты 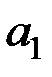 и
и 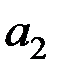 с помощью
с помощью 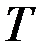 − критерия Стьюдента.
− критерия Стьюдента.
Имеем 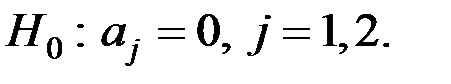
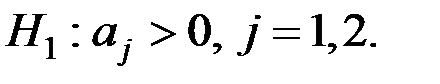
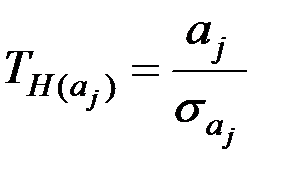 ,
,
где 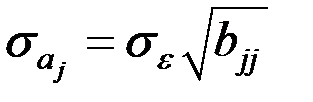 ,
, 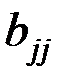 − диагональные элемента матрицы
− диагональные элемента матрицы 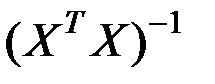 ,
,
Вычислим дисперсию остатков модели по соотношению

Точность модели (средняя ошибка)
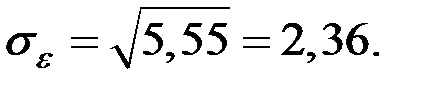
Тогда:
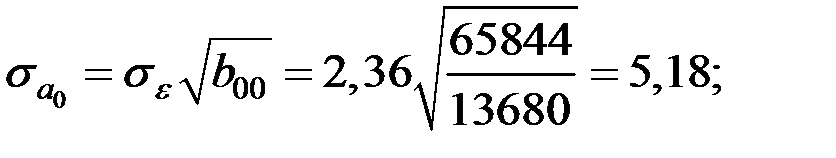
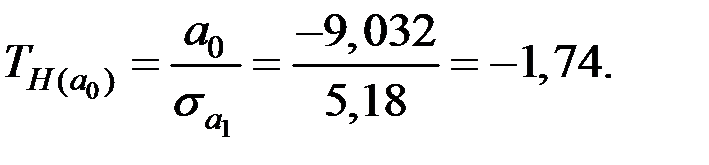
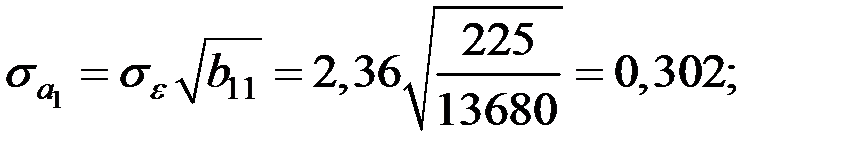
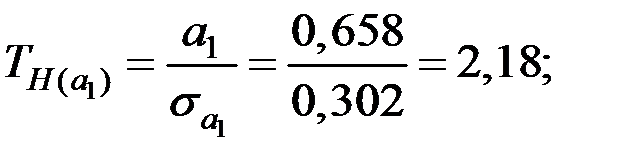
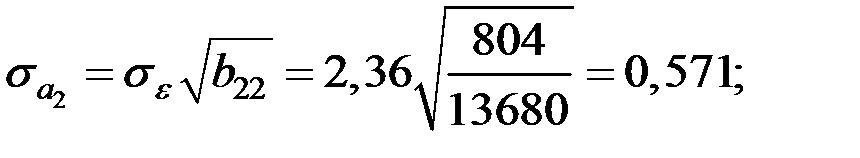
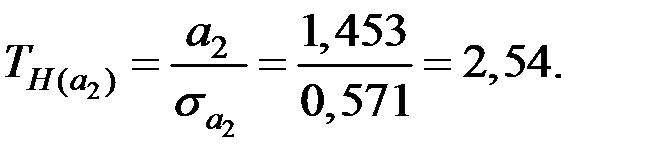
По таблице квантилей  −распределения Стьюдента найдём критическую точку:
−распределения Стьюдента найдём критическую точку: 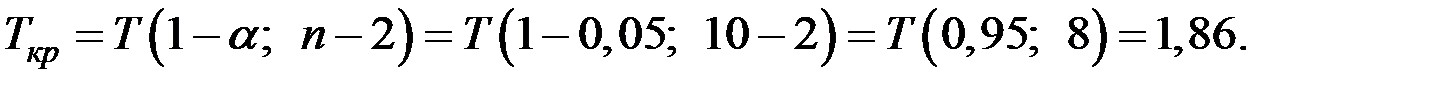
Так как 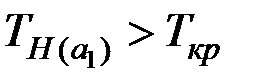 и
и 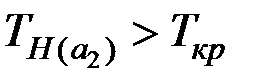 , то гипотезу
, то гипотезу 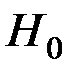 отвергаем, т.е. коэффициенты
отвергаем, т.е. коэффициенты 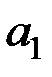 и
и 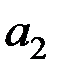 значимы,
значимы, 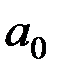 – не значим.
– не значим.
Точность модели можно оценить средней относительной ошибкой.
Промежуточные расчёты сведём в таблицу:
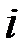
| 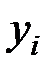
| 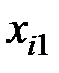
| 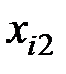
| 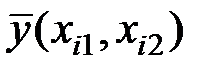
|
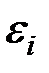
| 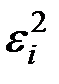
| 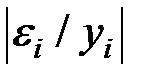
|
| 1 | 11 | 15 | 6 | 9,556 | 1,444 | 2,085 | 0,131 |
| 2 | 21 | 20 | 9 | 17,205 | 3,795 | 14,402 | 0,181 |
| 3 | 22 | 23 | 10 | 20,632 | 1,368 | 1,871 | 0,062 |
| 4 | 15 | 18 | 7 | 12,983 | 2,017 | 4,068 | 0,134 |
| 5 | 10 | 16 | 8 | 13,120 | –3,120 | 9,734 | 0,312 |
| 6 | 12 | 17 | 9 | 15,231 | –3,231 | 10,439 | 0,269 |
| 7 | 13 | 18 | 7 | 12,983 | 0,017 | 0,0003 | 0,001 |
| 8 | 9 | 19 | 5 | 10,735 | –1,735 | 3,010 | 0,193 |
| 9 | 12 | 16 | 6 | 10,214 | 1,786 | 3,190 | 0,149 |
| 10 | 16 | 24 | 8 | 18,384 | –2,384 | 5,683 | 0,149 |
| Итого: | 54,482 | 1,582 |
Тогда исходя из расчётов в таблице, получим:
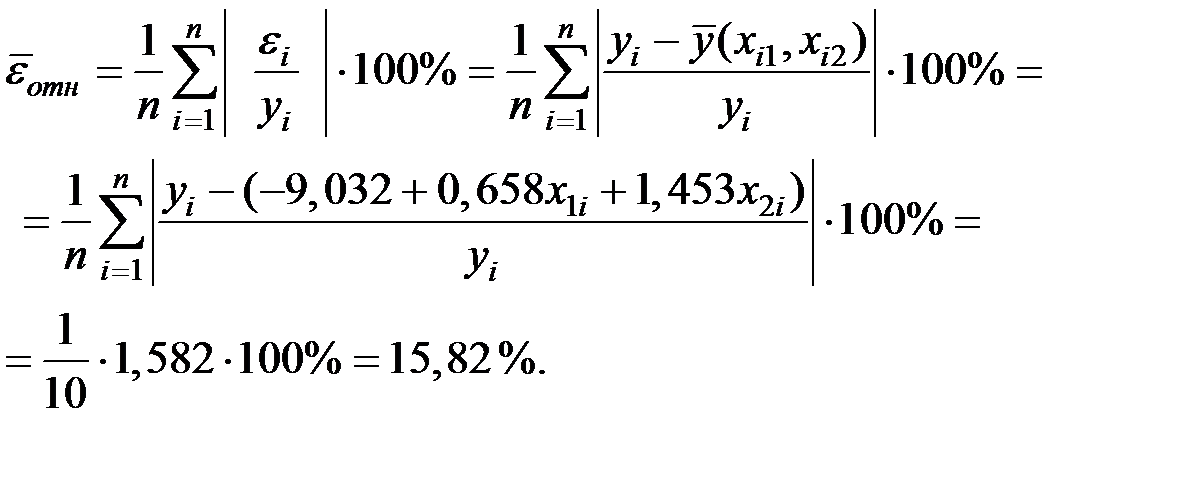
В среднем расчётные значения  для линейной модели отличаются от фактических значений на 15,82%.
для линейной модели отличаются от фактических значений на 15,82%.
Абсолютная ошибка при этом 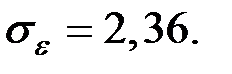
Пример 5.8. Имеются 12 наблюдений за тремя показателями:
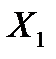
| 64 | 57 | 65 | 51 | 56 | 58 | 63 | 54 | 59 | 67 | 55 | 60 |
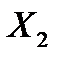
| 63 | 80 | 79 | 64 | 73 | 81 | 70 | 66 | 76 | 68 | 78 | 69 |
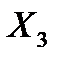
| 18 | 9 | 10 | 15 | 17 | 11 | 12 | 7 | 20 | 14 | 8 | 16 |
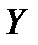
| 262 | 206 | 233 | 208 | 242 | 222 | 231 | 170 | 272 | 254 | 230 | 245 |
Используя пакет SPSS для обработки статистических данных получить уравнение множественной линейной регрессии и проанализировать качество полученной модели.
Решение. Построим уравнение в виде
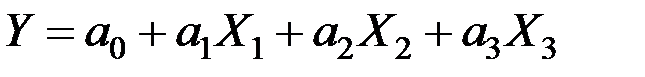 .
.
Вывод основных результатов выглядит следующим образом:






Основные числовые характеристики исследуемых показателей будут следующие: 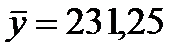 ;
; 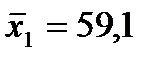 ;
; 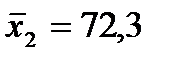 ;
; 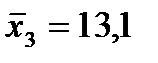 ;
;
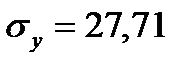 ;
; 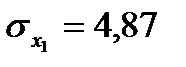 ;
; 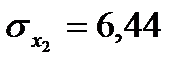 ;
; 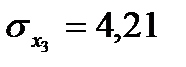 .
.
Параметры модели регрессии представлены в таблице «Coefficients».
Таким образом уравнение множественной регрессии имеет вид:
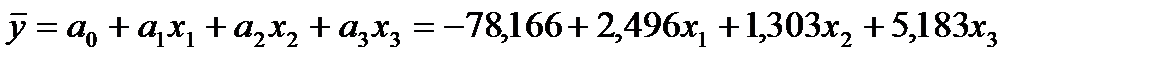 .
.
Для сравнения влияния каждой независимой переменной вычислим стандартизированные коэффициенты регрессии:
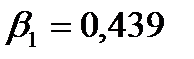 ;
; 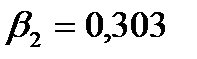 ;
; 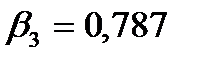 .
.
Увеличение показателя 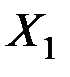 только на одно значение
только на одно значение 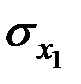 увеличивает в среднем показатель
увеличивает в среднем показатель 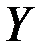 на
на 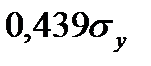 .
.
Аналогично, увеличение 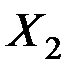 на значение
на значение 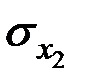 увеличивает
увеличивает 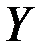 на
на 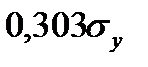 . Увеличение
. Увеличение 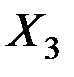 на
на 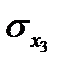 увеличивает
увеличивает 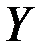 на
на 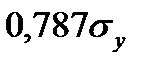 .
.
Коэффициенты эластичности составят величины:
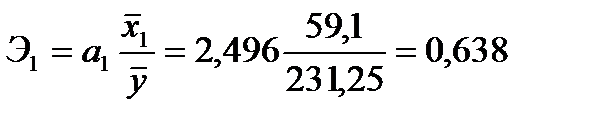 ;
;
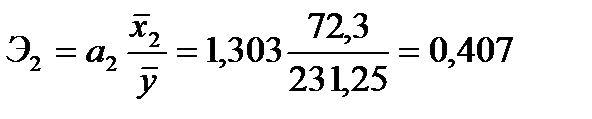 ;
;
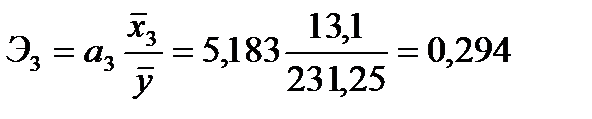 .
.
Увеличение переменных 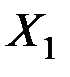 ,
, 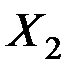 и
и 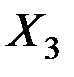 на 1% от своих средних значений приводит в среднем к увеличению
на 1% от своих средних значений приводит в среднем к увеличению 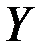 соответственно на 0,638%, 0,407% и 0,294%.
соответственно на 0,638%, 0,407% и 0,294%.
Проверим значимость модель множественной регрессии по 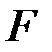 − критерию.
− критерию. 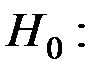 уравнение не значимо.
уравнение не значимо.
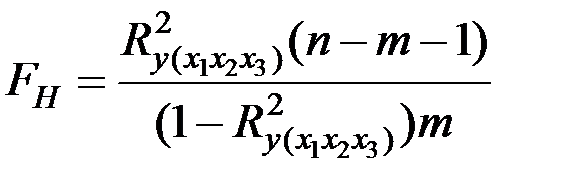 ,
,
где 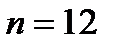 − количество наблюдений,
− количество наблюдений, 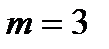 − количество показателей.
− количество показателей.
Коэффициент детерминации модели 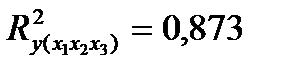 .
.
Наблюдаемое значение критерия 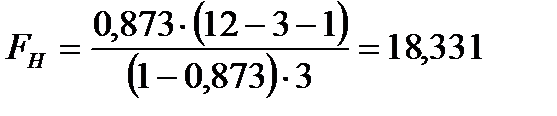 .
.
Отметим, что вычисления в пакете SPSS 13 дают то же значение
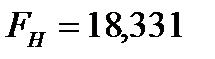 .
.
По таблице 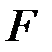 −распределения найдём критическую точку
−распределения найдём критическую точку
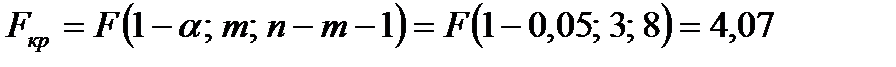 .
.
Так как 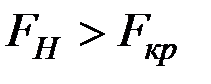 , то есть все основания отвергнуть гипотезу
, то есть все основания отвергнуть гипотезу 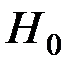 , т.е. модель регрессии значима при уровне значимости
, т.е. модель регрессии значима при уровне значимости 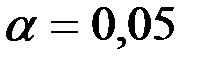 .
.
Проверим на значимость коэффициенты 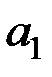 ,
, 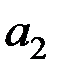 и
и 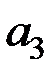 с помощью
с помощью 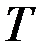 − критерия Стьюдента.
− критерия Стьюдента.
Имеем 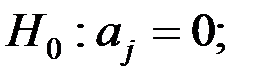
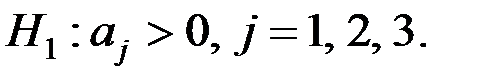
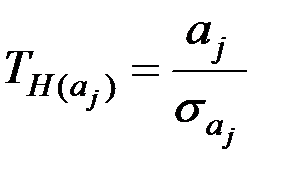 ,
,
где 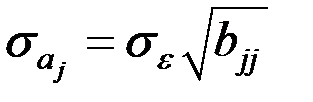 ,
, 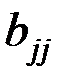 − диагональные элемента матрицы
− диагональные элемента матрицы 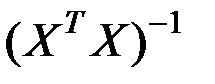 .
.
Вычислим дисперсию остатков модели по соотношению
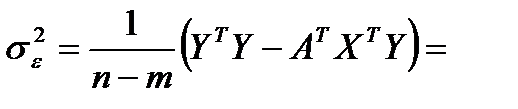
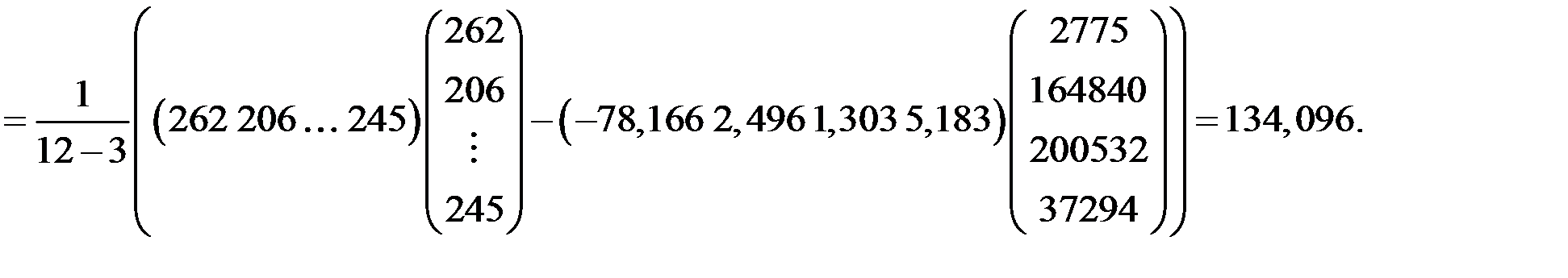
Средняя ошибка (точность) модели
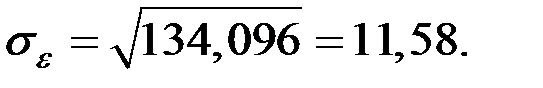
Тогда:
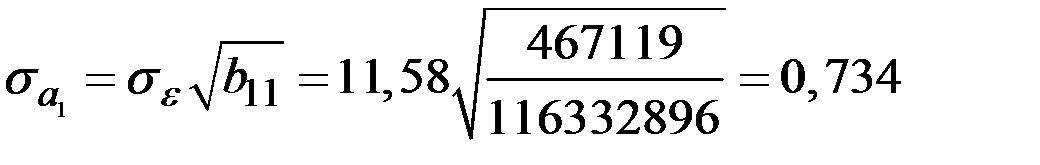 ;
; 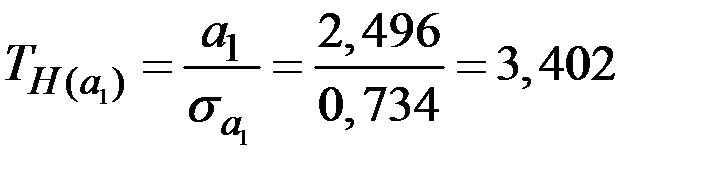 ;
;
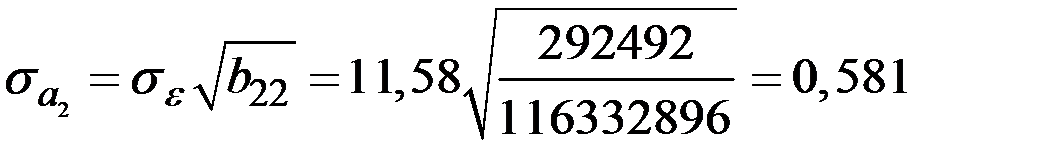 ;
; 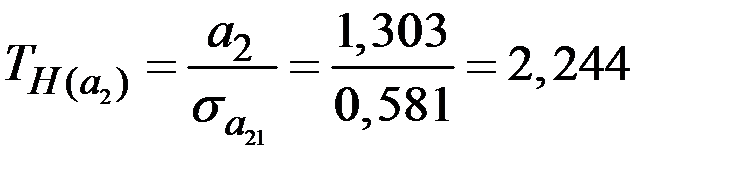 ;
;
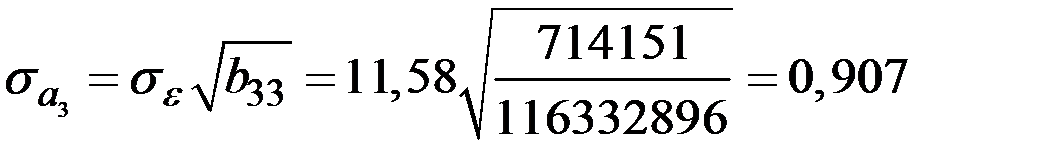 ;
; 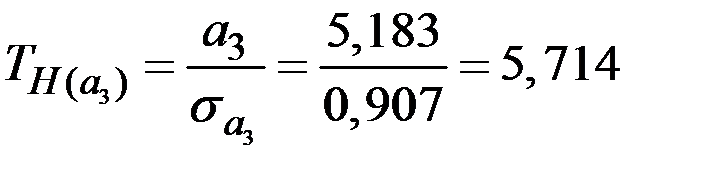 .
.
По таблице квантилей 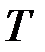 − распределения Стьюдента найдём критическую точку.
− распределения Стьюдента найдём критическую точку.
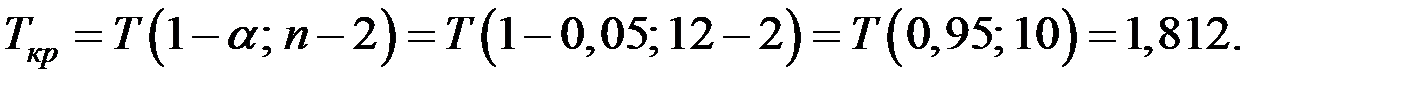
Так как 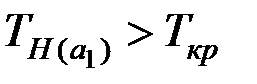 ,
, 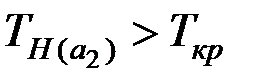 ,
, 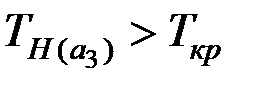 , то есть основания отвергнуть гипотезу
, то есть основания отвергнуть гипотезу 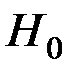 , т.е. все коэффициенты
, т.е. все коэффициенты 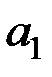 ,
, 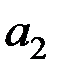 ,
, 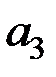 значимы.
значимы.
Контрольные вопросы к главе 5
1. В чём различие между корреляционной и функциональной связью?
2. Какие основные проблемы и каким образом решает исследователь при изучении регрессионных зависимостей?
3. Как проверяются гипотезы в регрессионном анализе?
4. Что характеризуют коэффициенты регрессии?
5. Как подходить к отбору факторов для включения их в уравнение множественной регрессии?
6. Какая существует связь между линейным коэффициентом корреляции и коэффициентами регрессии?
7. Каким образом оценить точность полученной модели регрессии?
8. Какими критериями пользуются при оценке качества построенной регрессионной модели?
9. Как строятся доверительные интервалы регрессионной модели?
10. Может ли регрессия нелинейная по параметрам быть приведена к линейному виду?
11. Что такое функциональная, стохастическая и статистическая связи между показателями?
12. Как осуществляется прогноз по регрессионной модели?
13. Поясните методику использования метода наименьших квадратов при построении регрессионной модели.
ЗАДАНИЕ 5.1. По имеющимся данным (табл. 5.2) получить уравнение линейной регрессии 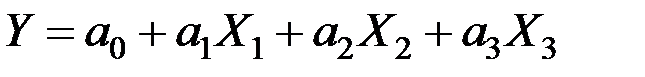 и проанализировать качество полученной модели. При выполнении данного задания целесообразно использовать какой–либо статистический пакет по обработке данных.
и проанализировать качество полученной модели. При выполнении данного задания целесообразно использовать какой–либо статистический пакет по обработке данных.
Таблица 5.2
Варианты задания для многомерного регрессионного анализа
| № вар. | Значения показателей | ||||||||||||
|
1 | 
| 3,1 | 3,4 | 2,8 | 2,9 | 3 | 2,7 | 3,2 | 3,1 | 3,5 | 4 | 2,6 | 3,4 |

| 15 | 12 | 13 | 11 | 18 | 20 | 18 | 20 | 14 | 13 | 10 | 12 | |

| 0,6 | 0,4 | 0,6 | 0,5 | 0,8 | 1 | 1,3 | 0,9 | 0,4 | 0,3 | 0,6 | 0,8 | |

| 13,5 | 16,2 | 14,6 | 15,9 | 13 | 11,5 | 18,4 | 11,3 | 14,1 | 16,8 | 16 | 20 | |
|
2 | 
| 3 | 3,5 | 4,6 | 3,2 | 4,3 | 3,4 | 3,9 | 3,1 | 3,5 | 4,7 | 4,1 | 3,3 |

| 0,1 | 0,3 | 0,8 | 0,2 | 0,1 | 0,3 | 0,5 | 0,3 | 0,1 | 0,9 | 0,6 | 0,7 | |

| 1,5 | 1,3 | 1,8 | 1,3 | 1,7 | 1,5 | 1,1 | 1,4 | 1,9 | 1,4 | 1,2 | 1,7 | |

| 1,5 | 4,3 | 10,1 | 3,1 | 5,4 | 4,2 | 7,1 | 3,2 | 2,2 | 11,9 | 8,3 | 5,2 | |
|
3 | 
| 1,4 | 1,7 | 1,3 | 1,4 | 1,3 | 1,1 | 1,7 | 1,2 | 1,6 | 1,4 | 1,2 | 1,5 |

| 16 | 9 | 16 | 8 | 10 | 15 | 8 | 16 | 11 | 15 | 8 | 12 | |

| 0,3 | 0,8 | 0,2 | 0,1 | 0,3 | 0,5 | 0,3 | 0,7 | 0,4 | 0,7 | 0,9 | 0,6 | |

| 10,1 | 5,8 | 9,3 | 1,3 | 3,4 | 9,1 | 2,6 | 11,2 | 5,9 | 10,1 | 4,2 | 7,3 | |
|
4 | 
| 23 | 32 | 26 | 29 | 20 | 29 | 23 | 26 | 34 | 24 | 36 | 29 |

| 8 | 6 | 5 | 9 | 5 | 8 | 6 | 5 | 9 | 6 | 5 | 7 | |

| 38 | 34 | 41 | 44 | 37 | 43 | 36 | 39 | 45 | 37 | 41 | 37 | |

| 114 | 91 | 136 | 128 | 133 | 124 | 118 | 129 | 117 | 125 | 119 | 107 | |
|
5 | 
| 91 | 122 | 110 | 93 | 125 | 109 | 113 | 95 | 120 | 97 | 121 | 103 |

| 438 | 422 | 423 | 424 | 410 | 439 | 413 | 430 | 432 | 419 | 437 | 420 | |

| 204 | 219 | 231 | 206 | 222 | 218 | 207 | 223 | 233 | 211 | 216 | 228 | |

| 960 | 841 | 621 | 854 | 740 | 901 | 888 | 691 | 666 | 777 | 987 | 604 | |
|
6 | 
| 16 | 18 | 20 | 17 | 18 | 16 | 19 | 20 | 18 | 21 | 19 | 16 |

| 0,3 | 0,4 | 0,6 | 0,5 | 0,8 | 0,6 | 0,1 | 0,9 | 0,4 | 0,3 | 0,6 | 0,8 | |

| 9,4 | 8,8 | 9,3 | 8,3 | 9,2 | 8,9 | 8,5 | 9,4 | 9,5 | 8,6 | 8,9 | 9 | |

| 0,2 | 3,5 | 5,1 | 3,8 | 4 | 2 | 4,1 | 5,7 | 2,2 | 6,2 | 5,3 | 2,4 | |
|
7 | 
| 0,79 | 0,86 | 0,94 | 0,85 | 0,95 | 0,81 | 0,88 | 0,91 | 0,83 | 0,96 | 0,84 | 0,89 |

| 3,03 | 3,22 | 3,33 | 3,05 | 3,07 | 3,19 | 3,34 | 3,09 | 3,41 | 3,12 | 3,15 | 3,37 | |

| 1,19 | 0,99 | 1,26 | 0,97 | 1,36 | 1,41 | 1,04 | 1,43 | 1,39 | 1,29 | 1,07 | 1,14 | |

| 1,69 | 3,05 | 2,34 | 2,77 | 1,55 | 1,18 | 3,15 | 1,18 | 1,75 | 1,96 | 2,54 | 2,84 | |
|
8 | 
| 3,3 | 3,1 | 2,8 | 2,9 | 3 | 2,7 | 3,6 | 3,1 | 3,5 | 4 | 2,6 | 3,4 |

| 8,8 | 9,5 | 8,5 | 8,9 | 8,6 | 8,1 | 9,5 | 9,1 | 8,3 | 8,7 | 8,9 | 8,3 | |

| 3,8 | 3,1 | 4 | 3,7 | 3,4 | 3,9 | 3,5 | 3,2 | 3,8 | 4 | 3,9 | 3,3 | |

| 9,3 | 14 | 5,5 | 8,3 | 10 | 4,7 | 14 | 13,2 | 9 | 10,4 | 5,9 | 12,3 | |
|
9 | 
| 3,5 | 3,2 | 3,1 | 3,5 | 4 | 2,6 | 3,4 | 2,9 | 3,7 | 3,3 | 2,6 | 3,4 |

| 14 | 13 | 10 | 12 | 13 | 16 | 17 | 20 | 14 | 13 | 19 | 12 | |

| 0,9 | 0,6 | 0,7 | 0,5 | 0,8 | 1 | 1,3 | 0,9 | 0,9 | 1 | 1,2 | 0,8 | |

| 19,9 | 15 | 19,3 | 17,1 | 21 | 14 | 20,6 | 10,5 | 20,5 | 20,7 | 13 | 19,8 | |
|
10 | 
| 0,59 | 0,71 | 0,79 | 0,61 | 0,69 | 0,76 | 0,57 | 0,65 | 0,77 | 0,62 | 0,78 | 0,67 |

| 0,03 | 0,15 | 0,13 | 0,21 | 0,06 | 0,16 | 0,07 | 0,13 | 0,18 | 0,08 | 0,23 | 0,09 | |

| 1,28 | 1,22 | 1,29 | 1,26 | 1,01 | 1,27 | 1,32 | 1,03 | 1,33 | 1,09 | 1,17 | 1,19 | |

| 26,1 | 28,8 | 30,1 | 28,7 | 23,8 | 29,7 | 27,4 | 24,8 | 30,7 | 24,3 | 29,6 | 26,1 | |
|
11 | 
| 1,2 | 1,6 | 1,4 | 1,9 | 1,5 | 1,8 | 1,2 | 1,3 | 1,7 | 1,4 | 1,2 | 1,5 |

| 15 | 8 | 16 | 11 | 15 | 8 | 12 | 13 | 13 | 14 | 8 | 12 | |

| 0,7 | 0,4 | 0,7 | 0,9 | 0,6 | 0,7 | 0,9 | 0,1 | 0,4 | 0,7 | 0,9 | 0,6 | |

| 10,4 | 2,9 | 11,4 | 8,5 | 10 | 4,4 | 8 | 6,3 | 8,1 | 9,3 | 4 | 7,4 | |
|
12 | 
| 3,5 | 3,7 | 3,2 | 3,1 | 3,9 | 3,7 | 3,8 | 3,1 | 3,4 | 3,9 | 3,1 | 3,6 |

| 0,3 | 0,1 | 0,5 | 0,6 | 0,7 | 0,1 | 0,4 | 0,7 | 0,2 | 0,4 | 0,3 | 0,7 | |

| 1,4 | 1,1 | 1,5 | 1,1 | 1,7 | 1,2 | 1,2 | 1,3 | 1,9 | 1,8 | 1,6 | 1,3 | |

| 5,7 | 4,3 | 6,8 | 5,9 | 8,5 | 4,7 | 6,2 | 6,8 | 7 | 7,9 | 6 | 7,3 | |
|
13 | 
| 20 | 32 | 26 | 35 | 20 | 30 | 23 | 27 | 37 | 24 | 39 | 29 |

| 15 | 14 | 18 | 16 | 11 | 15 | 17 | 12 | 18 | 13 | 19 | 14 | |

| 35 | 39 | 35 | 45 | 42 | 38 | 34 | 41 | 44 | 37 | 43 | 36 | |

| 77 | 78 | 48 | 80 | 125 | 69 | 56 | 89 | 63 | 85 | 49 | 65 | |
|
14 | 
| 20 | 28 | 14 | 29 | 16 | 33 | 23 | 30 | 34 | 25 | 32 | 27 |

| 41 | 57 | 49 | 42 | 59 | 55 | 44 | 53 | 58 | 47 | 54 | 48 | |

| 14 | 11 | 19 | 15 | 12 | 16 | 19 | 12 | 17 | 13 | 15 | 18 | |

| 87 | 109 | 103 | 117 | 81 | 150 | 127 | 115 | 166 | 100 | 137 | 143 | |
|
15 | 
| 12,1 | 10,4 | 11,6 | 12,6 | 10,6 | 11,4 | 11,9 | 10,9 | 12,8 | 12 | 11 | 11,3 |

| 7,4 | 8,2 | 9 | 7,6 | 8,8 | 8,3 | 7,7 | 9,1 | 7,8 | 8,4 | 8,2 | 8,8 | |

| 3,1 | 4,6 | 4,3 | 5,3 | 3,8 | 5,1 | 3,9 | 4,6 | 4 | 3,7 | 4,2 | 4 | |

| 87 | 82 | 90 | 92 | 84 | 88 | 87 | 87,4 | 92,4 | 90 | 85 | 87,9 | |
|
16 | 
| 9,7 | 8,9 | 9,6 | 8,1 | 9,9 | 9,7 | 9,2 | 8,3 | 9,4 | 8,4 | 9,4 | 8,6 |

| 13,3 | 13,6 | 13,8 | 14,4 | 14 | 14,6 | 13,9 | 14,7 | 14,1 | 13,4 | 14,3 | 13,4 | |

| 22,5 | 21 | 22 | 20 | 21,5 | 20,5 | 23 | 21,5 | 20,5 | 22 | 20 | 23,5 | |

| 41,6 | 42,1 | 40,4 | 42,3 | 38,1 | 36,6 | 46 | 46,7 | 37,6 | 46,4 | 37 | 48 | |
|
17 | 
| 3,4 | 3,2 | 3,6 | 3,9 | 3,7 | 3,1 | 3,9 | 3,7 | 3,8 | 3,1 | 3,9 | 3,4 |

| 0,3 | 0,5 | 0,6 | 0,8 | 0,1 | 0,4 | 0,7 | 0,8 | 0,4 | 0,2 | 0,7 | 0,3 | |

| 1,4 | 1,1 | 1,4 | 1,9 | 1,4 | 1,2 | 1,6 | 1,3 | 1,9 | 1,7 | 1,9 | 1,4 | |

| 5,7 | 5,4 | 7 | 10 | 5,3 | 5,3 | 8,5 | 7,8 | 8 | 6 | 9,3 | 5,5 | |
|
18 | 
| 16 | 13 | 10 | 20 | 19 | 14 | 11 | 17 | 15 | 12 | 18 | 13 |

| 7 | 11 | 6 | 3 | 5 | 9 | 3 | 8 | 6 | 5 | 4 | 8 | |

| 3 | 4 | 4 | 2 | 9 | 2 | 1 | 3 | 1 | 7 | 5 | 6 | |

| 7 | 8 | 14 | 3 | 20 | 3 | 10 | 5 | 3 | 22 | 15 | 17 | |
|
19 | 
| 18 | 9 | 10 | 15 | 17 | 11 | 12 | 7 | 20 | 14 | 8 | 16 |

| 63 | 80 | 79 | 64 | 73 | 81 | 70 | 66 | 76 | 68 | 78 | 69 | |

| 23 | 28 | 15 | 29 | 16 | 33 | 24 | 30 | 34 | 27 | 32 | 29 | |

| 150 | 173 | 98 | 183 | 119 | 209 | 147 | 167 | 240 | 172 | 191 | 194 | |
|
20 | 
| 3,6 | 4,6 | 4,3 | 5,3 | 3,8 | 4,9 | 3,9 | 4,6 | 4,1 | 3,8 | 4,5 | 4 |

| 7,6 | 8,2 | 9 | 7,9 | 9,1 | 8,3 | 7,7 | 9,8 | 7,8 | 8,9 | 9 | 8,8 | |

| 17,5 | 19,6 | 19,4 | 17,6 | 19,9 | 18 | 18,3 | 18,3 | 19,4 | 17,4 | 18,9 | 19 | |

| 60 | 68 | 68,8 | 68,4 | 67 | 68,4 | 61,9 | 71,1 | 64,3 | 64,1 | 70 | 66,1 | |
|
21 | 
| 7,4 | 8,2 | 9 | 7,6 | 8,8 | 8,3 | 7,7 | 9,1 | 7,8 | 8,4 | 7,9 | 9,1 |

| 13,9 | 14,7 | 14,1 | 13,4 | 14,3 | 13,4 | 13,9 | 14,9 | 14 | 13,9 | 14,6 | 14,7 | |

| 11 | 12 | 17 | 20 | 14 | 8 | 16 | 17 | 15 | 14 | 16 | 19 | |

| 18,1 | 18,9 | 29 | 45,4 | 21,3 | 4,9 | 32,5 | 29,3 | 29 | 22,4 | 33,1 | 35,2 | |
|
22 | 
| 10,5 | 9,3 | 9,7 | 9,2 | 10,1 | 9,4 | 10,3 | 9,1 | 9,4 | 10,3 | 9,2 | 10,2 |

| 2 | 2,8 | 2,6 | 2,9 | 2,1 | 3,1 | 2,6 | 2,4 | 2,7 | 3,1 | 2,5 | 2,7 | |

| 5,1 | 6,5 | 5,9 | 6,3 | 5,8 | 6,5 | 5,4 | 6,6 | 6 | 5,6 | 6,2 | 5,7 | |

| 29,1 | 39,6 | 34,4 | 35,5 | 36,6 | 36,1 | 28,5 | 43,1 | 34,7 | 27,7 | 38,3 | 31 | |
|
23 | 
| 21,3 | 22,9 | 22,4 | 23,1 | 21,3 | 22,4 | 21,4 | 23,4 | 22,6 | 21,5 | 22,8 | 20,8 |

| 32,4 | 32,8 | 30,9 | 33 | 32,1 | 31,4 | 30,1 | 31,8 | 30,4 | 33,2 | 31,9 | 30,5 | |

| 10,3 | 11,9 | 11,1 | 11,8 | 10,1 | 11,4 | 11,3 | 10,8 | 11,4 | 10,4 | 11,7 | 10,6 | |

| 50,3 | 52,3 | 45,4 | 52,9 | 48,1 | 50 | 49,1 | 41,2 | 46,6 | 52,5 | 49,9 | 48,1 | |
|
24 | 
| 4,5 | 4,1 | 4,6 | 4,1 | 4,2 | 4,6 | 4,2 | 4,3 | 4,8 | 4,4 | 4,5 | 4,5 |

| 0,3 | 0,5 | 0,3 | 0,7 | 0,4 | 0,7 | 0,9 | 0,6 | 0,7 | 0,9 | 0,1 | 0,3 | |

| 1,4 | 1,1 | 1,4 | 1,9 | 1,4 | 1,2 | 1,6 | 1,3 | 1,9 | 1,7 | 1,9 | 1,4 | |

| 7 | 6,3 | 7,1 | 9,6 | 6,8 | 8,2 | 10 | 7,6 | 10,3 | 10,1 | 7,6 | 6,6 | |
|
25 | 
| 64 | 57 | 65 | 51 | 56 | 58 | 63 | 54 | 59 | 67 | 55 | 60 |

| 63 | 80 | 79 | 64 | 73 | 81 | 70 | 66 | 76 | 68 | 78 | 69 | |

| 18 | 9 | 10 | 15 | 17 | 11 | 12 | 7 | 20 | 14 | 8 | 16 | |

| 262 | 206 | 233 | 208 | 242 | 222 | 231 | 170 | 272 | 254 | 190 | 245 | |
|
26 | 
| 3,6 | 3,5 | 4 | 2,6 | 3,4 | 2,9 | 3,7 | 3,3 | 4,1 | 3,9 | 4,6 | 3,2 |

| 10,6 | 11,4 | 11,9 | 10,9 | 12,8 | 13 | 11,4 | 10,9 | 13,1 | 11,8 | 11,3 | 12,5 | |

| 18,3 | 19,6 | 19,4 | 20,4 | 19,9 | 20,6 | 18,3 | 18,3 | 19,4 | 20,1 | 18,9 | 20,3 | |

| 69 | 72 | 77,1 | 67,1 | 76 | 75,1 | 72 | 68,9 | 82,2 | 78 | 76,8 | 74,8 | |
|
27 | 
| 23 | 32 | 26 | 29 | 20 | 29 | 23 | 26 | 34 | 24 | 36 | 29 |

| 14 | 12 | 15 | 13 | 11 | 16 | 11 | 16 | 14 | 12 | 13 | 15 | |

| 93 | 73 | 92 | 84 | 95 | 75 | 96 | 79 | 90 | 81 | 99 | 83 | |

| 304 | 220 | 296 | 263 | 333 | 212 | 334 | 239 | 272 | 266 | 300 | 244 | |
|
28 | 
| 10,5 | 11,3 | 11,7 | 11,2 | 10,9 | 11,4 | 10,3 | 11,1 | 11,4 | 10,3 | 11,2 | 10,2 |

| 3,6 | 3,2 | 4,9 | 4,6 | 3,8 | 3,2 | 4,7 | 3,9 | 3,4 | 4 | 3,5 | 4,3 | |

| 7,1 | 6,6 | 6 | 6,8 | 6,9 | 7,6 | 7 | 6,4 | 7,2 | 6,7 | 7,3 | 7,1 | |

| 39,6 | 36,3 | 17,2 | 27,5 | 34,4 | 45,3 | 29,9 | 28,6 | 39,9 | 31,7 | 41,3 | 33,7 | |
ЗАДАНИЕ 5.2. Имеются наблюдения за двумя показателями (см. варианты заданий). Исследовать взаимосвязь этих показателей с использованием ЭВМ. Требуется: 1) вычислить основные характеристики показателей (среднее значение, дисперсию, среднее квадратическое отклонение); 2) оценить тесноту взаимосвязи показателей, вычислив их коэффициент корреляции; 3) вычислить коэффициенты регрессионного уравнения; 4) оценить качество выполненного корреляционного и регрессионного анализа (проверить значимость коэффициента корреляции, адекватность и точность уравнения регрессии); 5) проанализировать полученные результаты.
Исходные данные к заданию 5.2:
| № вар | Исследуемые показатели | Значения показателей | |||||||
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 | ||
| 1 | Х1 , Х3 | 10,3 | 21,4 | 34,9 | 30,8 | 41,4 | 61,5 | 50,8 | 47,9 |
| 2 | Х2 , Х4 | 11,2 | 23,5 | 36,2 | 31,9 | 40,2 | 62,2 | 51,9 | 42,5 |
| 3 | Х3 , Х5 | 10,9 | 22,6 | 37,0 | 36,5 | 40,3 | 62,9 | 55,5 | 44,8 |
| 4 | Х4 , Х6 | 11,4 | 21,9 | 36,1 | 34,8 | 39,4 | 63,1 | 54,8 | 46,2 |
| 5 | Х5 , Х7 | 12,0 | 19,6 | 38,3 | 35,3 | 38,6 | 63,7 | 55,3 | 48,3 |
| 6 | Х6 , Х8 | 11,5 | 20,0 | 39,4 | 34,9 | 37,9 | 63,5 | 57,9 | 42,2 |
| 7 | Х1 , Х8 | 12,2 | 19,7 | 40,2 | 36,2 | 36,5 | 63,9 | 58,2 | 51,6 |
| 8 | Х2 , Х7 | 12,9 | 18,4 | 40,3 | 37,0 | 34,8 | 64,2 | 59,0 | 55,4 |
| 9 | Х3 , Х6 | 13,1 | 20,5 | 41,9 | 36,1 | 35,3 | 64,6 | 60,1 | 52,3 |
| 10 | Х4 , Х5 | 13,7 | 18,7 | 42,9 | 33,3 | 34,9 | 65,0 | 61,4 | 54,6 |
| 11 | Х1 , Х2 | 14,5 | 19,3 | 42,5 | 39,4 | 33,2 | 65,3 | 63,5 | 54,7 |
| 12 | Х2 , Х3 | 13,9 | 17,4 | 44,8 | 36,2 | 32,0 | 65,3 | 62,6 | 55,6 |
| 13 | Х3 , Х4 | 14,2 | 16,4 | 46,2 | 40,3 | 31,9 | 66,1 | 66,9 | 59,1 |
| 14 | Х4 , Х 8 | 14,6 | 18,9 | 48,3 | 41,9 | 30,5 | 67,9 | 69,6 | 51,0 |
| 15 | Х5 , Х6 | 15,0 | 16,2 | 49,9 | 47,9 | 29,5 | 66,4 | 72,9 | 54,3 |
| 16 | Х 6 , Х7 | 15,3 | 17,1 | 47,9 | 42,5 | 29,2 | 68,4 | 78,5 | 61,3 |
| 17 | Х7 , Х8 | 16,1 | 15,8 | 49,5 | 44,8 | 28,9 | 69,5 | 79,8 | 62,9 |
| 18 | Х8 , Х2 | 15,9 | 16,6 | 49,8 | 46,2 | 27,1 | 62,6 | 80,2 | 64,1 |
| 19 | Х7 , Х1 | 16,4 | 15,5 | 51,2 | 48,3 | 27,7 | 61,9 | 81,3 | 65,3 |
| 20 | Х6 , Х3 | 17,2 | 14,9 | 51,3 | 42,2 | 26,5 | 69,6 | 82,2 | 68,6 |
| 21 | Х1 , Х7 | 16,8 | 14,3 | 52,2 | 51,6 | 25,9 | 70,0 | 88,6 | 67,1 |
| 22 | Х2 , Х6 | 17,5 | 15,8 | 51,6 | 55,4 | 24,2 | 69,7 | 88,4 | 61,2 |
| 23 | Х3 , Х5 | 17,8 | 13,6 | 55,4 | 52,3 | 24,6 | 69,8 | 92,3 | 63,4 |
| 24 | Х4 , Х8 | 18,2 | 14,2 | 52,3 | 54,6 | 23,0 | 71,3 | 94,6 | 69,8 |
| 25 | Х3 , Х8 | 17,6 | 13,8 | 54,6 | 54,7 | 22,3 | 72,1 | 94,7 | 71,3 |
| 26 | Х5 , Х8 | 18,3 | 13,1 | 54,7 | 55,6 | 21,3 | 72,5 | 95,6 | 77,1 |
| 27 | Х6 , Х1 | 18,4 | 12,6 | 61,3 | 59,1 | 21,1 | 74,3 | 96,1 | 78,5 |
| 28 | Х5 , Х1 | 19,5 | 12,4 | 62,9 | 51,0 | 19,9 | 76,6 | 97,0 | 74,3 |
| 29 | Х4 , Х1 | 18,9 | 11,5 | 64,1 | 54,3 | 18,4 | 76,5 | 98,3 | 76,6 |
| 30 | Х7 , Х2 | 19,4 | 13,5 | 65,3 | 61,2 | 17,2 | 77,2 | 99,2 | 79,5 |
ЗАДАНИЕ 5.3. По имеющимся статистическим данным оценить и исследовать взаимосвязь между двумя показателями. Требуется:
1. Вычислить основные числовые характеристики каждой исследуемой переменной: математические ожидания, дисперсии, средние квадратические отклонения.
2. По имеющейся корреляционной таблице определить значение коэффициента корреляции двух показателей.
3. Получить уравнения регрессии и построить их графики.
4. Вычислить ожидаемое (прогнозное) значение одной величины при значении другой, равном математическому ожиданию соответствующей величины плюс два её средних квадратических отклонения.
5. Проанализировать полученные результаты.
ВАРИАНТЫ ЗАДАНИЯ
1. Зависимость между затратами на маркетинг и месячной прибылью фирмы
| Затраты на маркетинг, тыс.р. | Прибыль фирмы, млн. р. | ||||
| 2,0–2,2 | 2,2–2,4 | 2,4–2,6 | 2,6–2,8 | 2,8–3,0 | |
| 10 – 20 | 4 | – | – | – | – |
| 20 – 30 | 3 | 8 | 7 | – | – |
| 30 – 40 | – | 9 | 8 | 3 | 3 |
| 40 – 50 | – | 3 | 4 | 12 | 21 |
| Более 50 | – | – | 6 | 17 | 19 |
2. Взаимосвязь фондов и величиной валовой продукции предприятий
| Объём валовой | Годовая стоимость основных фондов, тыс. руб. | ||||
| продукции, тыс. руб. | До 80 | 80 – 100 | 100–120 | 120–140 | более 140 |
| До 50 | 6 | – | – | – | – |
| 50 – 70 | 2 | 3 | – | – | – |
| 70 – 90 | 5 | 6 | 2 | – | – |
| Более 90 | – | – | 4 | 3 | 11 |
3. Зависимость между затратами на рекламу и доходом фирмы
| Затраты на рекламу, тыс.р. | Доход, тыс. р. | ||||
| 100–150 | 150–200 | 200–250 | 250–300 | 300–350 | |
| 5 – 10 | 9 | – | – | 3 | – |
| 10 – 15 | 12 | 4 | 2 | 6 | 2 |
| 15 – 20 | 16 | 8 | 12 | 1 | 1 |
| 20 – 25 | – | 3 | 6 | 13 | 7 |
4. Распределение сотрудников по стажу и выполненному объёму работ
| Стаж работы, лет | Объём работы за год, тыс. р. | |||||
| 18–20 | 20–22 | 22–24 | 24–26 | 26–28 | 28–30 | |
| 0 – 5 | 17 | – | – | – | – | – |
| 5 – 10 | 6 | 3 | 1 | 4 | – | 3 |
| 10 – 15 | 4 | 5 | 7 | 8 | 1 | – |
| 15 – 20 | – | 8 | 6 | 2 | 8 | 1 |
| 20 – 25 | – | – | 3 | – | 9 | 20 |
5. Распределение производительности труда и объёма товарооборота
| Товарооборот на душу | Производительность труда, тыс. р/чел. | ||||
| населения, тыс. руб. | 15–20 | 20–25 | 25–30 | 30–35 | 35–40 |
| 0,7 – 0,9 | 18 | 1 | – | – | – |
| 0,9 – 1,1 | 4 | 12 | 23 | 1 | – |
| 1,1 – 1,3 | 3 | 7 | 16 | 13 | 6 |
| 1,3 – 1,5 | – | – | 2 | 17 | 14 |
6. Зависимость между рентабельностью собственных средств предприятия
и процентной ставкой за кредит
| Рентабельность, % | Процентная ставка, % | |||||
| 10–12 | 12–14 | 14–16 | 16–18 | 18–20 | 20–22 | |
| 18 – 20 | – | – | 2 | 1 | 3 | 4 |
| 20 – 22 | 2 | 3 | 9 | 2 | 2 | 1 |
| 22 – 24 | 7 | 6 | 4 | 1 | – | – |
| 24 – 26 | 3 | 1 | – | – | – | – |
7. Простои оборудования и себестоимость продукции за месяц
| Простои, ч. | Себестоимость, тыс. р. | ||||
| 5–5,2 | 5,2–5,4 | 5,4–5,6 | 5,6–5,8 | 5,8–6,0 | |
| 50 – 60 | 5 | 1 | – | 1 | – |
| 60 – 70 | 2 | 8 | 2 | 2 | 1 |
| 70 – 80 | 1 | 3 | 9 | 6 | 7 |
| 80 – 90 | – | – | 4 | 5 | 9 |
8. Распределение жилищного фонда на душу населения
и производительности труда в городах области (региона)
Жилищный фонд (  ) )
| Производительность труда, тыс. р/чел | ||||
| 14–18 | 18–22 | 22–26 | 26–30 | 30–34 | |
| Менее 9 | 2 | 1 | – | 2 | – |
| 9 – 12 | 9 | 7 | 3 | – | 1 |
| 12 – 15 | 4 | 14 | 7 | 1 | 2 |
| 15 – 18 | – | 3 | 18 | 13 | 3 |
| Более 18 | – | – | 2 | 2 | 6 |
9. Зависимость между затратами на НИР и себестоимостью продукции
| Затраты на НИР, тыс. р. | Себестоимость, тыс. р. | ||||
| 2,0–2,2 | 2,2–2,4 | 2,4–2,6 | 2,6–2,8 | 2,8–3,0 | |
| 10 – 20 | – | 6 | 1 | 4 | 9 |
| 20 – 30 | 3 | 12 | 17 | 8 | 2 |
| 30 – 40 | 8 | 19 | 13 | 13 | 3 |
| Более 40 | 14 | 16 | 4 | – | – |
10. Распределение населения по возрасту и количеству безработных
| Возраст, лет | Количество безработных, % | ||||
| 2,0–2,2 | 2,2–2,4 | 2,4–2,6 | 2,6–2,8 | 2,8–3,0 | |
| 20 – 30 | 12 | 2 | – | – | 1 |
| 30 – 40 | 3 | 16 | 6 | 2 | 3 |
| 40 – 50 | 4 | 5 | 12 | 3 | 15 |
| Более 50 | – | 1 | 9 | 18 | 28 |
11. Взаимосвязь объёма производства и затрат на управление фирмами
| Объем производства, | Затраты на управление, тыс. р/год | ||||
| млн. р/год | 50–60 | 60–70 | 70–80 | 80–90 | 90–100 |
| 6 | 8 | 2 | – | – | – |
| 6 – 7 | 2 | 4 | 6 | 3 | 4 |
| 7 – 8 | 1 | 7 | 10 | 8 | 6 |
| Более 8 | – | 2 | 4 | 7 | 12 |
12. Зависимость между экономической рентабельностью предприятия
и затратами на восстановление основных производственных фондов
| Рентабельность, % | Затраты на восстановление ОПФ, тыс. р. | ||||
| 2,0–2,2 | 2,2–2,4 | 2,4–2,6 | 2,6–2,8 | 2,8–3,0 | |
| 12 – 14 | 2 | 1 | 4 | 1 | 8 |
| 14 – 16 | 3 | 2 | 12 | 6 | 3 |
| 16 – 18 | 4 | 9 | 7 | 3 | 1 |
| 18 – 20 | 10 | 4 | 5 | 2 | – |
13. Взаимосвязь скорости движения автомобиля и расходом горючего
| Скорость движения, км/ч | Расход горючего на 100 км пути, л | ||||
| 7–8 | 8–9 | 9–10 | 10–11 | более 11 | |
| До 50 | 3 | – | – | 3 | 5 |
| 50 – 70 | 2 | 3 | 7 | 4 | – |
| 70 – 90 | 5 | 13 | 2 | – | – |
| 90 – 110 | 7 | 8 | 18 | 2 | – |
| Более 110 | – | – | 4 | 5 | 17 |
14. Распределение предприятий по величине собственных и заёмных средств
| Заёмные средства, | Собственные средства, тыс. р. | ||||
| тыс. р. | 250–300 | 300–350 | 350–400 | 400–450 | 450–500 |
| До 50 | – | 1 | 2 | 10 | 17 |
| 50 – 100 | 4 | 8 | 13 | 39 | 8 |
| 100 – 150 | 12 | 9 | 6 | 5 | 3 |
| 150 – 200 | 13 | 4 | 2 | – | – |
15. Распределение рабочих по стажу работы и месячной заработной плате
| Стаж работы, лет | Заработная плата, долл./мес. | ||||
| 130–160 | 160–190 | 190–210 | 210–240 | 240–270 | |
| До 10 | 14 | 7 | 4 | – | – |
| 10 – 15 | 1 | 16 | 12 | 5 | – |
| 15 – 20 | – | – | 3 | 10 | 19 |
| Более 20 | – | – | – | 18 | 39 |
16. Зависимость между количеством внесённых удобрений и урожайностью
| Количество удобрений, | Урожайность, ц/га | ||||
| ц/га | 20–22 | 22–24 | 24–26 | 26–28 | 28–30 |
| До 1 | 18 | – | – | 1 | 7 |
| 1 – 2 | 8 | 9 | 2 | 3 | 10 |
| 2 – 3 | 2 | 3 | 17 | 12 | 24 |
| 3 – 4 | 1 | – | 9 | 7 | 11 |
17. Распределение фирм по величине фондов и себестоимости продукции
| Основные фонды, млн. р | Себестоимость единицы продукции, р. | ||||
| 30–34 | 34–38 | 38–42 | 42–46 | 46–50 | |
| До 60 | – | – | – | – | 4 |
| 60 – 70 | – | 4 | 1 | 4 | 16 |
| 70 – 80 | 13 | 12 | 6 | 19 | 24 |
| 80 – 100 | 35 | 13 | 18 | 15 | – |
| Более 100 | 51 | 15 | 12 | 7 | – |
18. Зависимость между месячной прибылью фирмы и количеством
нарушений технологического процесса производства
| Количество нарушений | Месячная прибыль, тыс. р. | ||||
| технологического процесса | 200–300 | 300–400 | 400–500 | 500–600 | 600–700 |
| До 4 | – | – | 2 | 3 | 13 |
| 4 – 8 | 1 | 4 | 2 | 12 | 9 |
| 8 – 12 | 8 | 9 | 7 | – | 1 |
| Более 12 | 10 | – | – | – | – |
19. Зависимость между месячными затратами на рекламу и доходом фирмы
| Затраты на рекламу, тыс. р. | Доход, тыс. р. | ||||
| 100–150 | 150–200 | 200–250 | 250–300 | 300–350 | |
| До 10 | 9 | – | – | 1 | – |
| 10 – 15 | 12 | 4 | 2 | 6 | 2 |
| 15 – 20 | 16 | 8 | 12 | 8 | 9 |
| 20 – 25 | – | 3 | 6 | 13 | 7 |
20. Распределение сотрудников фирмы по стажу работы и выполненному
за год объёму работ
| Стаж, лет | Объём работы, тыс. р. | |||||
| 18–20 | 20–22 | 22–24 | 24–26 | 26–28 | 28–30 | |
| 0 – 5 | 3 | – | – | – | 6 | – |
| 5 – 10 | 15 | 3 | 1 | 4 | 2 | 3 |
| 10 – 15 | 4 | 15 | 27 | 8 | 1 | 12 |
| 15 – 20 | – | 8 | 16 | 2 | 22 | 16 |
| 20 – 25 | – | – | 3 | – | – | 30 |
21. Распределение магазинов по торговой площади и ежедневной выручкой
| Торговая площадь, | Ежедневная выручка, тыс. руб. | |||||
| (кв. метры) | 2–4 | 4–6 | 6–8 | 8–10 | 10–12 | более 12 |
| 10 – 30 | 2 | 2 | – | – | – | – |
| 30 – 50 | 6 | 3 | 3 | – | – | – |
| 50 – 70 | 4 | 8 | 6 | 1 | 2 | 1 |
| 70 – 90 | – | 4 | 7 | 2 | 4 | 8 |
| Более 90 | – | – | – | 2 | 3 | 10 |
22. Зависимость между рентабельностью собственных средств предприятия и средним износом оборудования
| Износ оборудования, | Рентабельность, % | |||||
| % | 10–12 | 12–14 | 14–16 | 16–18 | 18–20 | 20–22 |
| До 20 | – | – | 2 | 1 | 23 | 8 |
| 20–40 | 2 | 13 | 20 | 7 | 2 | 1 |
| 40–60 | 14 | 16 | 3 | 4 | – | – |
| Более 60 | 13 | 1 | – | – | – | – |
23. Простои оборудования и себестоимость продукции предприятия за месяц
| Простои, ч. | Себестоимость, тыс. р. | ||||
| 5–5,2 | 5,2–5,4 | 5,4–5,6 | 5,6–5,8 | 5,8–6,0 | |
| До 20 | 5 | 1 | – | – | – |
| 20 – 40 | 2 | 8 | 2 | 2 | 9 |
| 40 – 60 | 1 | 13 | 19 | 6 | 7 |
| 60 – 80 | – | – | 4 | 5 | 23 |
| Более 80 | – | – | 1 | 15 | 9 |
24. Зависимость между рентабельностью собственных средств предприятия и величиной заёмных средств
| Рентабельность, % | Заёмные средства, тыс. р. | ||||
| 200–300 | 300–400 | 400–500 | 500–600 | 600–700 | |
| 18 – 20 | – | – | 1 | 1 | 13 |
| 20 – 22 | 1 | 4 | 2 | 12 | 9 |
| 22 – 24 | 3 | 9 | 7 | 4 | 1 |
| 24 – 26 | 10 | 2 | – | – | – |
25. Распределение производительности труда и объёма товарооборота на душу населения
| Товарооборот, тыс. р. | Производительность труда, тыс. р/чел. | ||||
| 15–20 | 20–25 | 25–30 | 30–35 | 35–40 | |
| 0,7 – 0,9 | 2 | 1 | – | – | – |
| 0,9 – 1,1 | 4 | 5 | 3 | 1 | – |
| 1,1 – 1,3 | 3 | 7 | 6 | 5 | 6 |
| 1,3 – 1,5 | – | – | 2 | 7 | 3 |
| 1,5 – 1,7 | – | – | – | 6 | 5 |
МНОГОМЕРНЫЕ МЕТОДЫ АНАЛИЗА
Дата: 2019-03-05, просмотров: 712.