Экстраполяция - это метод научного исследования, который основан на распространении прошлых и настоящих тенденций, закономерностей, связей на будущее развитие объекта прогнозирования. К методам экстраполяции относятся метод скользящей средней, метод экспоненциального сглаживания, метод наименьших квадратов.

Метод экспоненциального сглаживания наиболее эффективен при разработке краткосрочных и среднесрочных прогнозов. Он приемлем при прогнозировании только на один период вперед. Его основные достоинства простота процедуры вычислений и возможность учета весов исходной информации.

 Рабочая формула метода экспоненциального сглаживания:

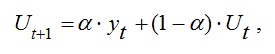где t – период, предшествующий прогнозному; t+1 – прогнозный период; Ut+1 - прогнозируемый показатель; α - параметр сглаживания; Уt - фактическое значение исследуемого показателя за период, предшествующий прогнозному; Ut - экспоненциально взвешенная средняя для периода, предшествующего прогнозному.

При прогнозировании данным методом возникает два затруднения:

- выбор значения параметра сглаживания α;

- определение начального значения Uo.

1) От величины α зависит, как быстро снижается вес влияния предшествующих наблюдений. Чем больше α, тем меньше сказывается влияние предшествующих лет. Если значение α близко к единице, то это приводит к учету при прогнозе в основном влияния лишь последних наблюдений. Если значение α близко к нулю, то веса, по которым взвешиваются уровни временного ряда, убывают медленно, т.е. при прогнозе учитываются все (или почти все) прошлые наблюдения.

Таким образом, если есть уверенность, что начальные условия, на основании которых разрабатывается прогноз, достоверны, следует использовать небольшую величину параметра сглаживания (α→0). Когда параметр сглаживания мал, то исследуемая функция ведет себя как средняя из большого числа прошлых уровней. Если нет достаточной уверенности в начальных условиях прогнозирования, то следует использовать большую величину α, что приведет к учету при прогнозе в основном влияния последних наблюдений.

Точного метода для выбора оптимальной величины параметра сглаживания α нет. В отдельных случаях автор данного метода профессор Браун предлагал определять величину α, исходя из длины интервала сглаживания. При этом α вычисляется по формуле:

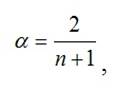где n – число наблюдений, входящих в интервал сглаживания.

2) Задача выбора Uo (экспоненциально взвешенного среднего начального) решается следующими способами:

- если есть данные о развитии явления в прошлом, то можно воспользоваться средней арифметической и приравнять к ней Uo;

- если таких сведений нет, то в качестве Uo используют исходное первое значение базы прогноза У1.

Также можно воспользоваться экспертными оценками.

Отметим, что при изучении экономических временных рядов и прогнозировании экономических процессов метод экспоненциального сглаживания не всегда «срабатывает». Это обусловлено тем, что экономические временные ряды бывают слишком короткими (15-20 наблюдений), и в случае, когда темпы роста и прироста велики, данный метод не «успевает» отразить все изменения.

Пример применения метода экспоненциального сглаживания для разработки прогноза

Задача. Имеются данные, характеризующие уровень безработицы в регионе, %

• Постройте прогноз уровня безработицы в регионе на ноябрь, декабрь, январь месяцы, используя методы: скользящей средней, экспоненциального сглаживания, наименьших квадратов.
• Рассчитайте ошибки полученных прогнозов при использовании каждого метода.
• Сравните полученные результаты, сделайте выводы.