Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается .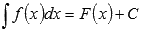

Выражение 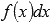называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).

Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.

На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).

1.
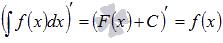
Производная результата интегрирования равна подынтегральной функции.

2.
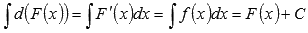
Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.

3. 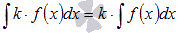, где k – произвольная константа.
Коэффициент можно выносить за знак неопределенного интеграла.

4.
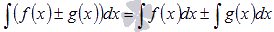
Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.

Промежуточные равенства первого и второго свойств неопределенного интеграла приведены для пояснения.

Для доказательства третьего и четвертого свойств достаточно найти производные от правых частей равенств:

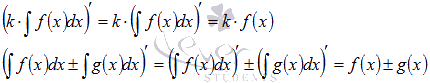
Эти производные равны подынтегральным функциям, что и является доказательством в силу первого свойства. Оно же используется в последних переходах.

Таким образом, задача интегрирования является обратной задаче дифференцирования, причем между этими задачами очень тесная связь:

· первое свойство позволяет проводить проверку интегрирования. Чтобы проверить правильность выполненного интегрирования достаточно вычислить производную полученного результата. Если полученная в результате дифференцирования функция окажется равной подынтегральной функции, то это будет означать, что интегрирование проведено верно;

· второе свойство неопределенного интеграла позволяет по известному дифференциалу функции найти ее первообразную. На этом свойстве основано непосредственное вычисление неопределенных интегралов.

Рассмотрим пример.

Пример.

Найти первообразную функции 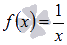, значение которой равно единице при х = 1.

Решение.

Мы знаем из дифференциального исчисления, что 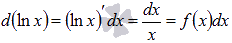(достаточно заглянуть в таблицу производных основных элементарных функций). Таким образом, 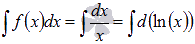. По второму свойству 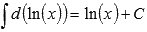. То есть, имеем множество первообразных 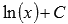. При х = 1 получим значение 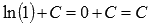. По условию, это значение должно быть равно единице, следовательно, С = 1. Искомая первообразная примет вид .

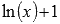Пример.

Найти неопределенный интеграл 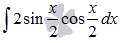и результат проверить дифференцированием.

Решение.

По формуле синуса двойного угла из тригонометрии 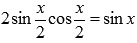, поэтому

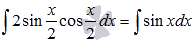
Из таблицы производных для тригонометрических функций имеем

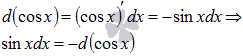
То есть,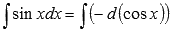

По третьему свойству неопределенного интеграла можем записать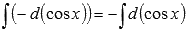

Обращаясь ко второму свойству, получим .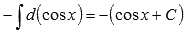

Следовательно,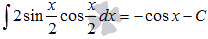

Проверка.

Для проверки результата продифференцируем полученное выражение:

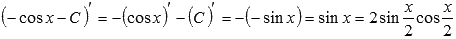
В итоге получили подынтегральную функцию, значит, интегрирование выполнено правильно. В последнем переходе была использована формула синуса двойного угла.