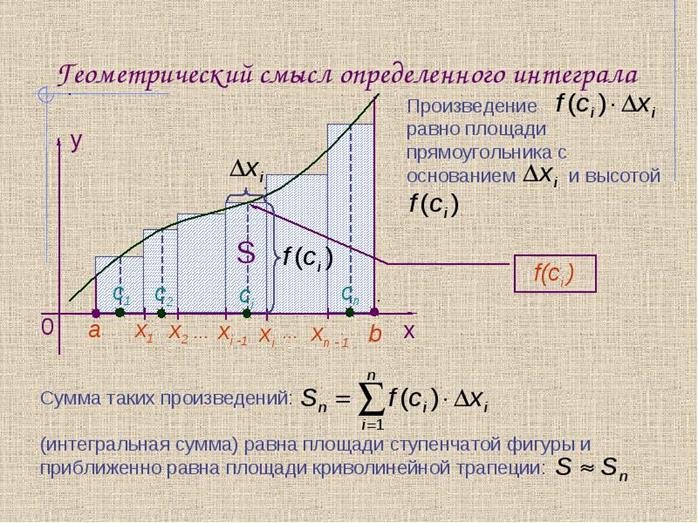
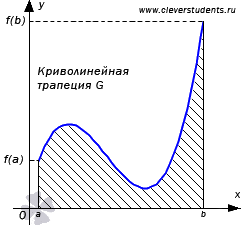
Пусть функция y = f(x) непрерывна на отрезке [a; b] и не меняет знак на нем (то есть, неотрицательная или неположительная). Фигуру G, ограниченную линиями y = f(x), y = 0, x = a и x = b, называют криволинейной трапецией. Обозначим ее площадь S(G).

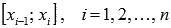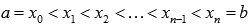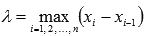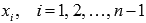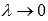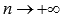Подойдем к задаче вычисления площади криволинейной трапеции следующим образом. В разделе квадрируемые фигуры мы выяснили, что криволинейная трапеция является квадрируемой фигурой. Если разбить отрезок [a; b] на n частей точками и обозначить , а точки выбирать так, чтобы при , то фигуры, соответствующие нижней и верхней суммам Дарбу, можно считать входящей P и объемлющей Q многоугольными фигурами для G.

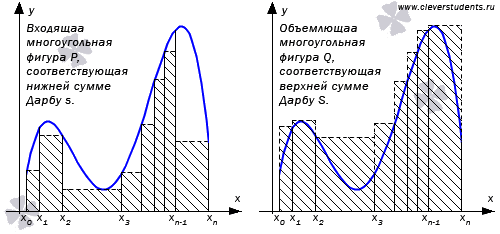
Таким образом, 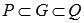и при увеличении количества точек разбиения n, мы придем к неравенству 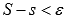, где 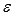- сколь угодно малое положительное число, а sи S – нижняя и верхняя суммы Дарбу для данного разбиения отрезка [a; b]. В другой записи 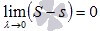. Следовательно, обратившись к понятию определенного интеграла Дарбу, получаем .

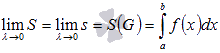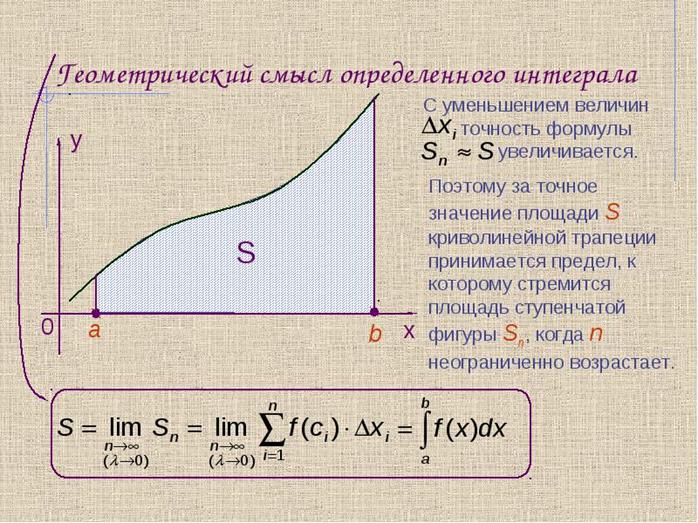
Последнее равенство означает, что определенный интеграл для непрерывной и неотрицательной функции y = f(x) представляет собой в геометрическом смысле площадь соответствующей криволинейной трапеции. В этом и состоит геометрический смысл определенного интеграла.

То есть, вычислив определенный интеграл , мы найдем площадь фигуры, ограниченной линиями y = f(x), y = 0, x = a и x = b.

Замечание.

Если функция y = f(x) неположительная на отрезке [a; b], то площадь криволинейной трапеции может быть найдена как .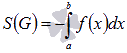

Пример.

Вычислить площадь фигуры, ограниченной линиями .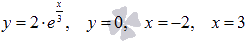

Решение.

Построим фигуру на плоскости: прямая y = 0 совпадает с осью абсцисс, прямые x = -2 и x = 3 параллельны оси ординат, а кривая 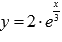может быть построена с помощью геометрических преобразований графика функции .

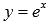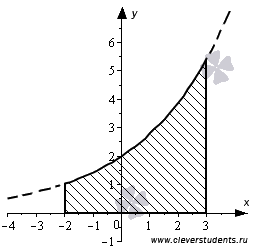
Таким образом, нам требуется найти площадь криволинейной трапеции. Геометрический смысл определенного интеграла нам указывает на то, что искомая площадь выражается определенным интегралом. Следовательно, 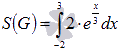. Этот определенный интеграл можно вычислить по формуле Ньютона-Лейбница:

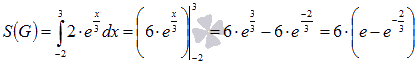
Замечание.

При нахождении площадей криволинейных трапеций совсем не обязательно сначала строить эту фигуру. Если Вы знаете, что функция y = f(x) неотрицательная на отрезке [a; b] (как в нашем примере) или неположительная, то можно сразу применять формулы 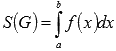или .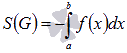

Пример.

Вычислить площадь фигуры, ограниченной линиями .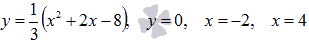

Решение.

Построим эту фигуру. Прямая y = 0 совпадает с осью Ox, прямые x = -2 и x = 4параллельны оси Oy, а графиком функции 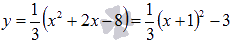является парабола с вершиной в точке (-1; -3) ветви которой направлены вверх. Найдем точки пересечения этой параболы с осью абсцисс:

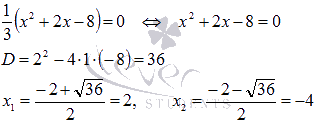
Следовательно, эта парабола пересекает ось абсцисс в точках (-4; 0) и (2; 0).

Таким образом, наша фигура G имеет следующий вид.

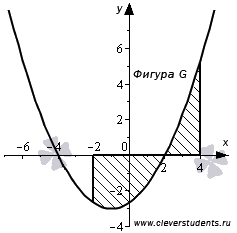
Эта фигура не является криволинейной трапецией, так как функция 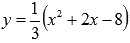меняет знак на отрезке [-2; 4].

Как же быть в этом случае? Очень просто. Фигуру G можно представить в виде объединения двух криволинейных трапеций 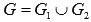и по свойству аддитивности площади .

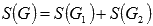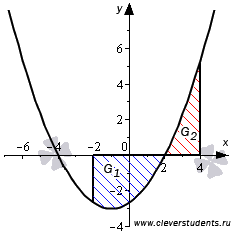
На отрезке [2; 4] график параболы находится в неотрицательной области, поэтому 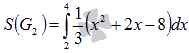. На отрезке [-2; 2] функция 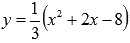неположительная, следовательно, в силу замечания к геометрическому смыслу определенного интеграла, имеем 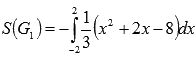. Осталось вычислить определенные интегралы по формуле Ньютона-Лейбница:

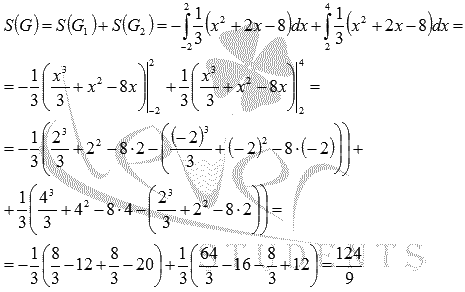
Обратите внимание на то, что нельзя находить площадь этой фигуры как .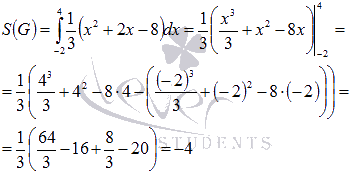

В нашем примере полученное таким образом значение представляет собой разность .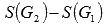

Фигуры, ограниченные линиями y = c, y = d, x = 0 и x = g(y), где функция x = g(y)непрерывна и не меняет знак на отрезке [c; d], также являются криволинейными трапециями.

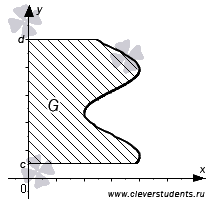
Геометрический смысл определенного интеграла 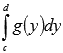состоит в том, что его значение равно площади криволинейной трапеции для непрерывной и неотрицательной функции x=g(y) на отрезке [c;d]. Также справедливо 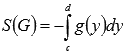для непрерывной и неположительной функции x=g(y) на отрезке [c;d].

Пример.

Вычислить площадь фигуры, ограниченной осью ординат и линиями .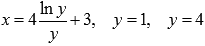

Решение.

Построить график функции 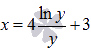не очень легко. Попробуем обойтись без этого. Эта функция определена для всех положительных значений аргумента y. Оценим значения функции на отрезке [1; 4]. Из свойств основных элементарных функций мы знаем, что функция натурального логарифма является возрастающей на всей своей области определения. Более того, на отрезке [1; 4] она неотрицательна, то есть, 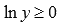. Выражение 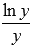на отрезке [1; 4] также будет неотрицательным, так как знаменатель является положительным числом на этом отрезке. Из этого можно заключить, что функция 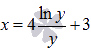является положительной на интервале [1; 4]. Поэтому фигура в этом примере является криволинейной трапецией, и ее площадь мы будем искать как .

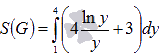Осталось вычислить определенный интеграл, для чего найдем одну из первообразных функции 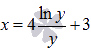и применим формулу Ньютона-Лейбница:

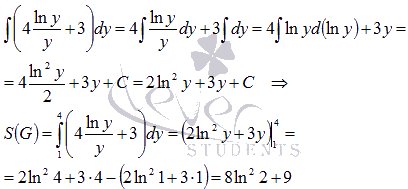
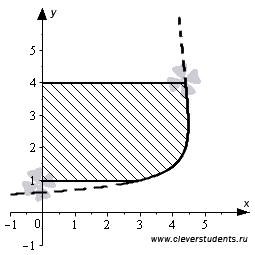
Для наглядности все же приведем чертеж.

Подведем итог.

Мы выяснили геометрический смысл определенного интеграла и обнаружили его связь с площадью криволинейной трапеции. Таким образом, мы получили возможность находить площади и более сложных фигур, которые можно представить объединением криволинейных трапеций.