Решение систем линейных уравнений методом гаусса
Понятие метода Гаусса
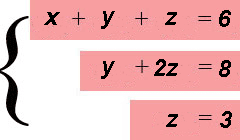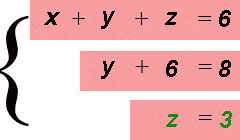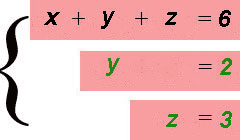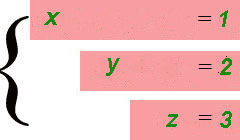
Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в следующем. При помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной (то же самое, что треугольной или ступенчатой) или близкой к трапециевидной (прямой ход метода Гаусса, далее - просто прямой ход). Пример такой системы и её решения - на рисунке сверху.
В такой системе последнее уравнение содержит только одну переменную и её значение можно однозначно найти. Затем значение этой переменной подставляют в предыдущее уравнение (обратный ход метода Гаусса, далее - просто обратный ход), из которого находят предыдущую переменную, и так далее.
В трапециевидной (треугольной) системе, как видим, третье уравнение уже не содержит переменных y и x, а второе уравнение - переменной x.
После того, как матрица системы приняла трапециевидную форму, уже не представляет труда разобраться в вопросе о совместности системы, определить число решений и найти сами решения.
Преимущества метода:
- при решении систем линейных уравнений с числом уравнений и неизвестных более трёх метод Гаусса не такой громоздкий, как метод Крамера, поскольку при решении методом Гаусса необходимо меньше вычислений;
- методом Гаусса можно решать неопределённые системы линейных уравнений, то есть, имеющие общее решение (и мы разберём их на этом уроке), а, используя метод Крамера, можно лишь констатировать, что система неопределённа;
- можно решать системы линейных уравнений, в которых число неизвестных не равно числу уравнений (также разберём их на этом уроке);
- метод основан на элементарных (школьных) методах - методе подстановки неизвестных и методе сложения уравнений, которых мы коснулись в соответствующей статье.
Кроме того, метод Гаусса является основой одного из методов нахождения обратной матрицы.
Чтобы все прониклись простотой, с которой решаются трапециевидные (треугольные, ступенчатые) системы линейных уравнений, приведём решение такой системы с применением обратного хода. Быстрое решение этой системы было показано на картинке в начале урока.
Пример 1. Решить систему линейных уравнений, применяя обратный ход:
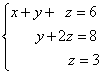
Решение. В данной трапециевидной системе переменная z однозначно находится из третьего уравнения. Подставляем её значение во второе уравнение и получаем значение переменой y:
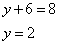
Теперь нам известны значения уже двух переменных - z и y. Подставляем их в первое уравнение и получаем значение переменной x:

Из предыдущих шагов выписываем решение системы уравнений:
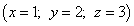
Чтобы получить такую трапециевидную систему линейных уравнений, которую мы решили очень просто, требуется применять прямой ход, связанный с элементарными преобразованиями системы линейных уравнений. Это также не очень сложно.
Пример 3. Решить систему линейных уравнений методом Гаусса:
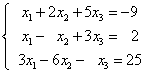
Решение. Подвергаем преобразованиям расширенную матрицу системы:
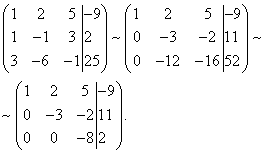
Таким образом, приходим к следующей системе уравнений:
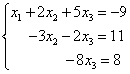
Эта система имеет единственное решение:
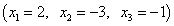
Формулы Крамера
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.
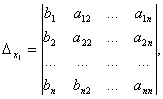
Определение. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается  (дельта).
(дельта).
Определители 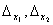
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
 ;
;
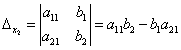 .
.
Формулы Крамера для нахождения неизвестных:
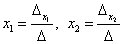 .
.
Найти значения  и
и 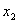 возможно только при условии, если
возможно только при условии, если
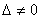 .
.
Этот вывод следует из следующей теоремы.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
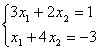 . (2)
. (2)
Согласно теореме Крамера имеем:
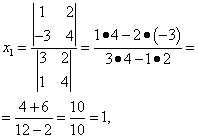
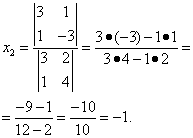
Итак, решение системы (2):
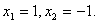
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.
Примеры решения систем линейных уравнений методом Крамера
Пусть дана система
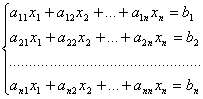 .
.
На основании теоремы Крамера
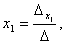
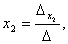
………….
 ,
,
где
 -
-
определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:


Уравнение прямой в отрезках
Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим: 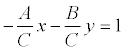 или
или
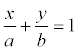 , где
, где
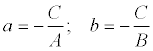
Геометрический смысл коэффициентов в том, что коэффициент аявляется координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.
Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.
С = 1,  , а = -1, b = 1.
, а = -1, b = 1.
Нормальное уравнение прямой
Если обе части уравнения Ах + Ву + С = 0 умножить на число 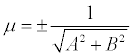 , которое называется нормирующем множителем , то получим
, которое называется нормирующем множителем , то получим
xcosφ + ysinφ - p = 0 –
нормальное уравнение прямой. Знак ± нормирующего множителя надо выбирать так, чтобы μ * С < 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.
Пример. Дано общее уравнение прямой 12х – 5у – 65 = 0. Требуется написать различные типы уравнений этой прямой.
уравнение этой прямой в отрезках: 
уравнение этой прямой с угловым коэффициентом: (делим на 5)
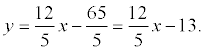
нормальное уравнение прямой:
 ; cos φ = 12/13; sin φ= -5/13; p = 5.
; cos φ = 12/13; sin φ= -5/13; p = 5.
Cледует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые, параллельные осям или проходящие через начало координат.
Пример. Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного этими отрезками равна 8 см 2 .
Решение. Уравнение прямой имеет вид: 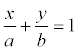 , ab /2 = 8; ab=16; a=4, a=-4. a = -4 < 0 не подходит по условию задачи. Итого:
, ab /2 = 8; ab=16; a=4, a=-4. a = -4 < 0 не подходит по условию задачи. Итого: 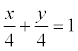 или х + у – 4 = 0.
или х + у – 4 = 0.
Пример. Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат.
Решение. Уравнение прямой имеет вид: 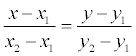 , где х 1 = у 1 = 0; x2 = -2; y2 = -3.
, где х 1 = у 1 = 0; x2 = -2; y2 = -3. 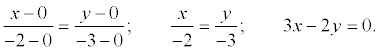
Общее уравнение плоскости.
Приведем формулировку теоремы, которая дает нам вид уравнения плоскости.
Теорема.
Всякое уравнение вида 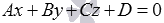 , где A, B, C и D – некоторые действительные числа, причем А, В и C одновременно не равны нулю, определяет плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве, и всякая плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве может быть задана уравнением вида
, где A, B, C и D – некоторые действительные числа, причем А, В и C одновременно не равны нулю, определяет плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве, и всякая плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве может быть задана уравнением вида 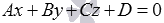 .
.
Уравнение 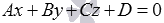 называется общим уравнением плоскости в пространстве. Если не придавать числам А, В, С и D конкретных значений, то общее уравнение плоскости называют уравнением плоскости в общем виде.
называется общим уравнением плоскости в пространстве. Если не придавать числам А, В, С и D конкретных значений, то общее уравнение плоскости называют уравнением плоскости в общем виде.
Следует заметить, что уравнение вида 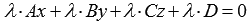 , где
, где 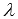 - некоторое действительное число, отличное от нуля, будет определять ту же самую плоскость, так как равенства
- некоторое действительное число, отличное от нуля, будет определять ту же самую плоскость, так как равенства 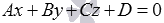 и
и 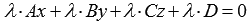 эквивалентны. К примеру, общие уравнения плоскости
эквивалентны. К примеру, общие уравнения плоскости 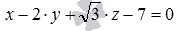 и
и 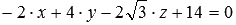 задают одну и ту же плоскость, так как им удовлетворяют координаты одних и тех же точек трехмерного пространства.
задают одну и ту же плоскость, так как им удовлетворяют координаты одних и тех же точек трехмерного пространства.
Немного поясним смысл озвученной теоремы. В прямоугольной системе координат Oxyz каждой плоскости соответствует ее уравнение общего вида 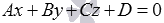 , а каждому уравнению
, а каждому уравнению 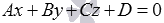 соответствует плоскость в заданной прямоугольной системе координат трехмерного пространства. Другими словами, плоскость и ее общее уравнение неразделимы.
соответствует плоскость в заданной прямоугольной системе координат трехмерного пространства. Другими словами, плоскость и ее общее уравнение неразделимы.
Если все коэффициенты А, В, С и D в общем уравнении плоскости 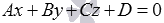 отличны от нуля, то оно называется полным. В противном случае, общее уравнение плоскости называется неполным.
отличны от нуля, то оно называется полным. В противном случае, общее уравнение плоскости называется неполным.
Замечание.
Предел функции f(x) при 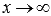 бесконечен, если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции является бесконечно большой положительной или бесконечно большой отрицательной. Обозначается
бесконечен, если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции является бесконечно большой положительной или бесконечно большой отрицательной. Обозначается 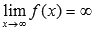 .
.
Пример.
Используя определение предела при 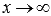 доказать равенство
доказать равенство 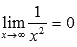 .
.
Решение.
Запишем последовательность значений функции  для бесконечно большой положительной последовательности значений аргумента
для бесконечно большой положительной последовательности значений аргумента 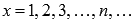 .
.
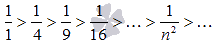
Очевидно, что члены этой последовательности монотонно убывают к нулю.
Графическая иллюстрация.
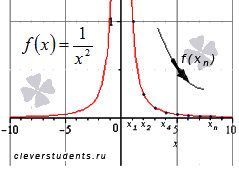
Теперь запишем последовательность значений функции  для бесконечно большой отрицательной последовательности значений аргумента
для бесконечно большой отрицательной последовательности значений аргумента 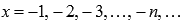 .
.
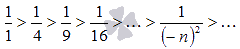
Члены этой последовательности также монотонно убывают к нулю, что доказывает исходное равенство.
Графическая иллюстрация.
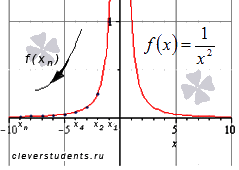
Пример.
Найти предел 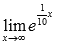
Решение.
Запишем последовательность значений функции  для бесконечно большой положительной последовательности значений аргумента. К примеру, возьмем
для бесконечно большой положительной последовательности значений аргумента. К примеру, возьмем 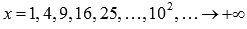 .
.
Последовательность значений функции при этом будет (синие точки на графике)
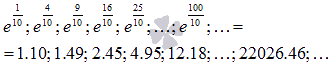
Очевидно, что эта последовательность является бесконечно большой положительной, следовательно, 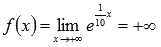
А сейчас запишем последовательность значений функции  для бесконечно большой отрицательной последовательности значений аргумента. К примеру, возьмем
для бесконечно большой отрицательной последовательности значений аргумента. К примеру, возьмем  .
.
Последовательность значений функции при этом будет (зеленые точки на графике)

Очевидно, что эта последовательность сходится к нулю, следовательно, 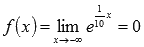
Графическая иллюстрация
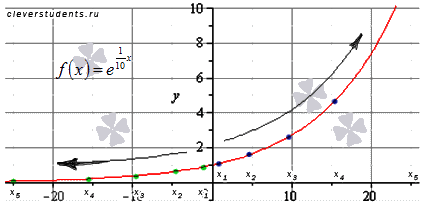
Ответ:
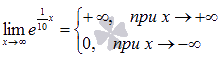
Сейчас поговорим о существовании и нахождении предела функции в точке. Все основывается на определении односторонних пределов. Без вычисления односторонних пределов не обойтись при нахождении вертикальных асимптот графика функции.
Определение (нахождение предела функции слева).
Число В называется пределом функции f(x) слева при 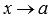 , если для любой сходящейся к а последовательности аргументов функции
, если для любой сходящейся к а последовательности аргументов функции  , значения которых остаются меньше а (
, значения которых остаются меньше а (  ), последовательность значений этой функции сходится к В.
), последовательность значений этой функции сходится к В.
Обозначается 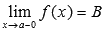 .
.
Определение (нахождение предела функции справа).
Число В называется пределом функции f(x) справа при 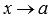 , если для любой сходящейся к а последовательности аргументов функции
, если для любой сходящейся к а последовательности аргументов функции  , значения которых остаются больше а (
, значения которых остаются больше а ( 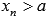 ), последовательность значений этой функции сходится к В.
), последовательность значений этой функции сходится к В.
Обозначается 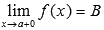 .
.
Определение (существование предела функции в точке).
Предел функции f(x) в точке а существует, если существуют пределы слева и справа а и они равны между собой.
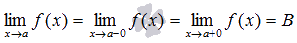
Замечание.
Предел функции f(x) в точке а бесконечен, если пределы слева и справа абесконечны.
Поясним эти определения на примере.
Пример.
Доказать существование конечного предела функции 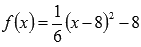 в точке
в точке 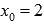 . Найти его значение.
. Найти его значение.
Решение.
Будем отталкиваться от определения существования предела функции в точке.
Во-первых, покажем существование предела слева. Для этого возьмем последовательность аргументов  , сходящуюся к
, сходящуюся к 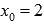 , причем
, причем 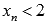 . Примером такой последовательности может являться
. Примером такой последовательности может являться
Соответствующая последовательность значений функции будет иметь вид
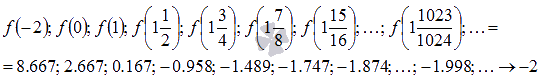
На рисунке соответствующие значения показаны зелеными точками.
Легко видеть, что эта последовательность сходится к -2, поэтому 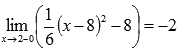 .
.
Во-вторых, покажем существование предела справа. Для этого возьмем последовательность аргументов  , сходящуюся к
, сходящуюся к 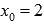 , причем
, причем 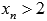 . Примером такой последовательности может являться
. Примером такой последовательности может являться
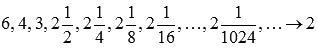
Соответствующая последовательность значений функции будет иметь вид
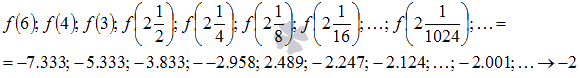
На рисунке соответствующие значения показаны синими точками.
Легко видеть, что эта последовательность также сходится к -2, поэтому 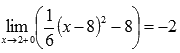 .
.
Этим мы показали, что пределы слева и справа равны, следовательно, по определению существует предел функции 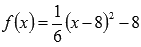 в точке
в точке 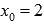 , причем
, причем 
Графическая иллюстрация.

Следствие.
ЗНАЧЕНИЕ ПРЕДЕЛА ФУНКЦИИ В ТОЧКАХ НЕПРЕРЫВНОСТИ СОВПАДАЕТ СО ЗНАЧЕНИЕМ ФУНКЦИИ В ЭТИХ ТОЧКАХ.
Пример.
Доказать непрерывность функции 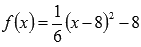 в точке
в точке 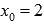 .
.
Решение.
Во-первых, покажем существование предела слева. Для этого возьмем последовательность аргументов  , сходящуюся к
, сходящуюся к 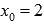 , причем
, причем 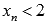 . Примером такой последовательности может являться
. Примером такой последовательности может являться
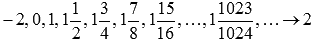
Соответствующая последовательность значений функции будет иметь вид
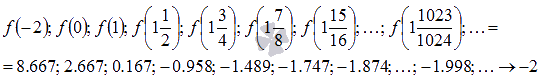
На рисунке соответствующие значения показаны зелеными точками.
Легко видеть, что эта последовательность сходится к -2, поэтому 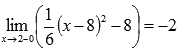 .
.
Во-вторых, покажем существование предела справа. Для этого возьмем последовательность аргументов  , сходящуюся к
, сходящуюся к 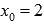 , причем
, причем 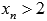 . Примером такой последовательности может являться
. Примером такой последовательности может являться
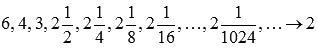
Соответствующая последовательность значений функции будет иметь вид
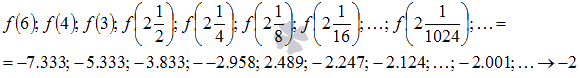
На рисунке соответствующие значения показаны синими точками.
Легко видеть, что эта последовательность также сходится к -2, поэтому 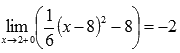 .
.
Этим мы показали, что пределы слева и справа равны, следовательно, существует предел функции 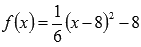 в точке
в точке 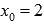 , причем
, причем 
Вычислив значение функции в точке 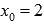 можно говорить о выполнении равенства
можно говорить о выполнении равенства 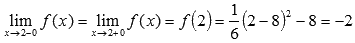 , это доказывает непрерывность исходной функции в точке.
, это доказывает непрерывность исходной функции в точке.
Графическая иллюстрация.

Определение устранимого разрыва первого рода.
В точке 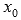 функция имеет устранимый разрыв первого рода, если предел слева равен пределу справа, но они не равны значению функции в точке ,то есть
функция имеет устранимый разрыв первого рода, если предел слева равен пределу справа, но они не равны значению функции в точке ,то есть 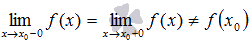 .
.
Пример.
Найти точки разрыва функции и определить их тип 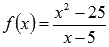 .
.
Решение.
Находим область определения функции:
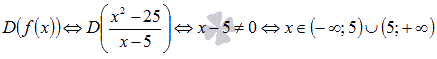
Точкой разрыва нашей функции может быть только граничная точка области определения, то есть  . Проверим функцию на непрерывность в этой точке.
. Проверим функцию на непрерывность в этой точке.
На области определения выражение 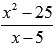 можно упростить:
можно упростить:
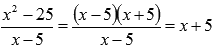
Находим пределы слева и справа. Так как функция 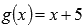 непрерывна при любом действительном х, то
непрерывна при любом действительном х, то

Следовательно, пределы слева и справа равны, а сама функция 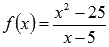 в точке
в точке  не определена, поэтому, в точке
не определена, поэтому, в точке  функция имеет устранимый разрыв первого рода.
функция имеет устранимый разрыв первого рода.
Определение неустранимого разрыва первого рода (точка скачка функции).
В точке 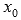 функция имеет неустранимый разрыв первого рода, если пределы слева и справа НЕ равны, то есть
функция имеет неустранимый разрыв первого рода, если пределы слева и справа НЕ равны, то есть 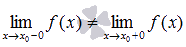 . Точку
. Точку 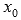 в этом случае называют точкой скачка функции.
в этом случае называют точкой скачка функции.
Пример.
Исследовать кусочно-непрерывную функцию  на непрерывность, определить вид точек разрыва, сделать чертеж.
на непрерывность, определить вид точек разрыва, сделать чертеж.
Решение.
Разрывы могут быть лишь в точках 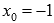 или
или  .
.
Найдем пределы слева и справа от этих точек, а также значения исходной функции в этих точках.
Слева от точки 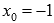 наша функция есть
наша функция есть 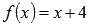 и в силу непрерывности линейной функции
и в силу непрерывности линейной функции 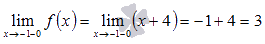 .
.
В самой точке 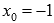 наша функция есть
наша функция есть 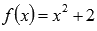 , поэтому
, поэтому 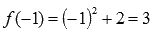 .
.
На промежутке 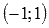 наша функция есть
наша функция есть 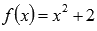 и в силу непрерывности квадратичной функции
и в силу непрерывности квадратичной функции

В точке  наша функция есть
наша функция есть  , поэтому
, поэтому 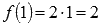 .
.
Справа от  наша функция есть
наша функция есть  и в силу непрерывности линейной функции
и в силу непрерывности линейной функции
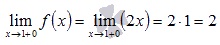
В итоге имеем:
· 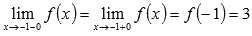 следовательно, в точке
следовательно, в точке 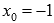 исходная кусочная функция непрерывна,
исходная кусочная функция непрерывна,
· 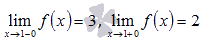 , то есть
, то есть 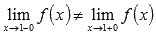 , следовательно, в точке
, следовательно, в точке  неустранимый разрыв первого рода (скачок).
неустранимый разрыв первого рода (скачок).
Графическая иллюстрация.

Определение разрыва второго рода (бесконечный разрыв).
В точке 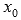 функция имеет разрыв второго рода, если либо предел слева
функция имеет разрыв второго рода, если либо предел слева  , либо предел справа
, либо предел справа 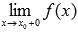 , не существует или бесконечен.
, не существует или бесконечен.
Пример.
Исследовать функцию 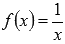 на непрерывность, определить вид точек разрыва, сделать чертеж.
на непрерывность, определить вид точек разрыва, сделать чертеж.
Решение.
Областю определения функции является интервал 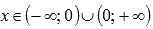 .
.
Найдем пределы функции слева и справа от точки 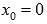 .
.
Рассмотрим произвольную последовательность значений аргумента, сходящуюся к 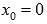 слева. Например,
слева. Например,  и соответствующую ей последовательность значений функции
и соответствующую ей последовательность значений функции
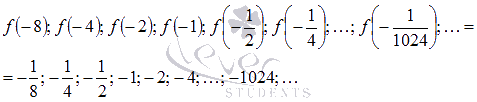
Легко показать, что эта последовательность бесконечно большая отрицательная, поэтому, 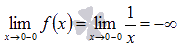 .
.
Рассмотрим произвольную последовательность значений аргумента, сходящуюся к 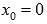 справа. Например,
справа. Например, 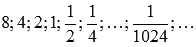 и соответствующую ей последовательность значений функции
и соответствующую ей последовательность значений функции
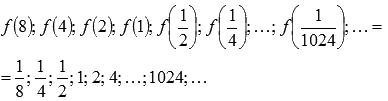
Легко показать, что эта последовательность бесконечно большая положительная, поэтому, 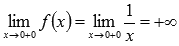 .
.
Следовательно, в точке 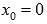 функция имеет разрыв второго рода.
функция имеет разрыв второго рода.
Графическая иллюстрация.

Пример 5.1.
Найти область определения функции 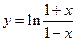 .
.
Решение. Выражение, стоящее в правой части равенства, имеет смысл, если аргумент натурального логарифма больше нуля, а знаменатель дроби не равен нулю. То есть
 и
и 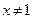 .
.
Исследуя левую часть неравенства можно построить интервалы ее положительного и отрицательного значений.
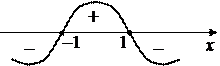
|
Из рисунка видно, что областью решений неравенства является интервал (–1; 1). Следовательно, область определения исходной функции: x 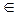 (–1; 1).
(–1; 1).
На отрезке

На первом рисунке функция принимает наибольшее (max y) и наименьшее (min y) значения в стационарных точках, находящихся внутри отрезка [-6;6].
Рассмотрим случай, изображенный на втором рисунке. Изменим отрезок на [1;6]. В этом примере наименьшее значение функции достигается в стационарной точке, а наибольшее - в точке с абсциссой, соответствующей правой границе интервала.
На рисунке №3 граничные точки отрезка [-3;2] являются абсциссами точек, соответствующих наибольшему и наименьшему значению функции.
На открытом интервале
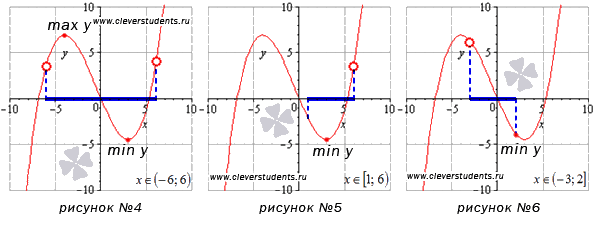
На четвертом рисунке функция принимает наибольшее (max y) и наименьшее (min y) значения в стационарных точках, находящихся внутри открытого интервала (-6;6).
На интервале [1;6) наименьшее значение функции достигается в стационарной точке, а про наибольшее значение мы ничего сказать не можем. Если бы точка x=6была частью интервала, тогда при этом значении функция принимала бы наибольшее значение. Этот пример изображен на рисунке №5.
На рисунке №6 наименьшее значение функции достигается в правой границе интервала (-3;2], о наибольшем значении никаких выводов сделать нельзя.
На бесконечности

В примере, представленном на седьмом рисунке, функция принимает наибольшее значение (max y) в стационарной точке с абсциссой x=1, а наименьшее значение (min y) достигается на правой границе интервала. На минус бесконечности значения функции асимптотически приближаются к y=3.
На интервале 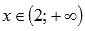 функция не достигает ни наименьшего, ни наибольшего значения. При стремлении к x=2 справа значения функции стремятся к минус бесконечности (прямая x=2 является вертикальной асимптотой), а при стремлении абсциссы к плюс бесконечности, значения функции асимптотически приближаются к y=3. Графическая иллюстрация этого примера приведена на рисунке №8
функция не достигает ни наименьшего, ни наибольшего значения. При стремлении к x=2 справа значения функции стремятся к минус бесконечности (прямая x=2 является вертикальной асимптотой), а при стремлении абсциссы к плюс бесконечности, значения функции асимптотически приближаются к y=3. Графическая иллюстрация этого примера приведена на рисунке №8
Алгоритм нахождения наибольшего и наименьшего значения непрерывной функции на отрезке [a;b].
Запишем алгоритм, позволяющий находить наибольшее и наименьшее значение функции на отрезке.
1. Находим область определения функции и проверяем, содержится ли в ней весь отрезок [a;b].
2. Находим все точки, в которых не существует первая производная и которые содержатся в отрезке [a;b] (обычно такие точки встечаются у функций с аргументом под знаком модуля и у степенных функций с дробно-рациональным показателем). Если таких точек нет, то переходим к следующему пункту.
3. Определяем все стационарные точки, попадающие в отрезок [a;b]. Для этого, находим производную функции, приравниваем ее к нулю, решаем полученное уравнение и выбираем подходящие корни. Если стационарных точек нет или ни одна из них не попадает в отрезок, то переходим к следующему пункту.
4. Вычисляем значения функции в отобранных стационарных точках (если такие имеются), в точках, в которых не существует первая производная (если такие имеются), а также при x=a и x=b.
5. Из полученных значений функции выбираем наибольшее и наименьшее - они и будут искомыми наибольшим и наименьшим значениями функции соответственно.
Разберем алгоритм при решении примера на нахождение наибольшего и наименьшего значения функции на отрезке.
Пример.
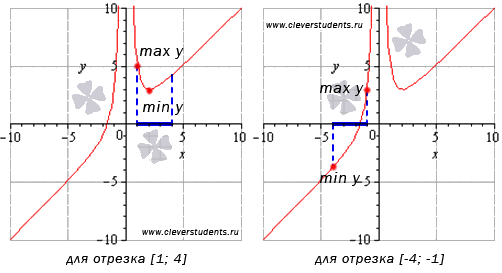
Найти наибольшее и наименьшее значение функции 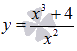
· на отрезке [1;4];
· на отрезке [-4;-1].
Решение.
Областью определения функции является все множество действительных чисел, за исключением нуля, то есть 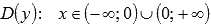 . Оба отрезка попадают в область определения.
. Оба отрезка попадают в область определения.
Находим производную функции по правилу дифференцирования дроби:
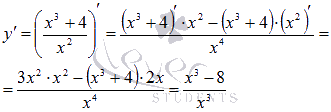
Очевидно, производная функции существует во всех точках отрезков [1;4] и [-4;-1].
Стационарные точки определим из уравнения 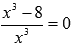 . Единственным действительным корнем является x=2. Эта стационарная точка попадает в первый отрезок [1;4].
. Единственным действительным корнем является x=2. Эта стационарная точка попадает в первый отрезок [1;4].
Для первого случая вычисляем значения функции на концах отрезка и в стационарной точке, то есть при x=1, x=2 и x=4:
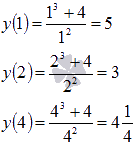
Следовательно, наибольшее значение функции 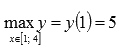 достигается при x=1, а наименьшее значение
достигается при x=1, а наименьшее значение 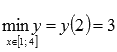 – при x=2.
– при x=2.
Для второго случая вычисляем значения функции лишь на концах отрезка [-4;-1] (так как он не содержит ни одной стационарной точки):

Следовательно, 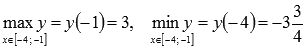 .
.
Графическая иллюстрация.
К началу страницы
Алгоритм нахождения наибольшего и наименьшего значения непрерывной функции на открытом или бесконечном интервале X.
Прежде чем ознакомиться с алгоритмом нахождения наибольшего и наименьшего значения функции на открытом или бесконечном интервале рекомендуем повторить определения одностороннего предела и предела на бесконечности, а также способы нахождения пределов.
1. Проверяем, является ли интервал X подмножеством области определения функции.
2. Находим все точки, в которых не существует первая производная и которые содержатся в интервале X (обычно такие точки встечаются у функций с аргументом под знаком модуля и у степенных функций с дробно-рациональным показателем). Если таких точек нет, то переходим к следующему пункту.
3. Определяем все стационарные точки, попадающие в промежуток X. Для этого приравниваем производную функции к нулю, решаем полученное уравнение и выбираем подходящие корни.
Если стационарных точек нет или ни одна из них не попадает в интервал, то переходим к следующему пункту.
4. Вычисляем значения функции в стационарных точках и точках, в которых не существует первая производная функции (если такие точки есть).
Дальнейшие действия зависят от интервала X.
Если интервал X имеет вид:
o [a;b), то вычисляем значение функции в точке x=a и односторонний предел  ;
;
o (a;b], то вычисляем значение функции в точке x=b и односторонний предел  ;
;
o (a;b), то вычисляем односторонние пределы  ;
;
o 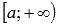 , то вычисляем значение функции в точке x=a и предел на плюс бесконечности
, то вычисляем значение функции в точке x=a и предел на плюс бесконечности 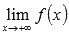 ;
;
o 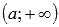 , то вычисляем односторонний предел
, то вычисляем односторонний предел  и предел на плюс бесконечности
и предел на плюс бесконечности 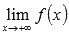 ;
;
o 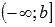 , то вычисляем значение функции в точке x=b и предел на минус бесконечности
, то вычисляем значение функции в точке x=b и предел на минус бесконечности 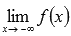 ;
;
o 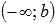 , то вычисляем односторонний предел
, то вычисляем односторонний предел  и предел на минус бесконечности
и предел на минус бесконечности 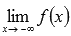 ;
;
o 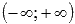 , то вычисляем пределы на плюс и минус бесконечности
, то вычисляем пределы на плюс и минус бесконечности 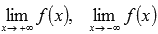 .
.
5. Делаем выводы, отталкиваясь от полученных значений функции и пределов. Здесь может быть масса вариантов. К примеру, если односторонний предел равен минус бесконечности (плюс бесконечности), то о наименьшем (наибольшем) значении функции ничего сказать нельзя для данного интервала. Ниже разобраны несколько типичных примеров. Надеемся подробные описания их решения помогут Вам усвоить тему. Рекомендуем вернуться к рисункам с №4 до №8 из первого раздела этой статьи.
Пример.
Найти наибольшее и наименьшее значение функции 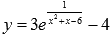 на интервалах:
на интервалах:
1. 
2. 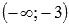
3. (-3;1]
4. (-3;2)
5. [1;2)
6. 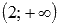
7. 
Решение.
Начнем с области определения функции. Квадратный трехчлен в знаменателе дроби не должен обращаться в ноль:
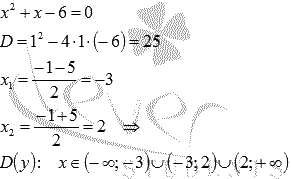
Легко проверить, что все интервалы из условия задачи принадлежат области определения функции.
Продифференцируем функцию:
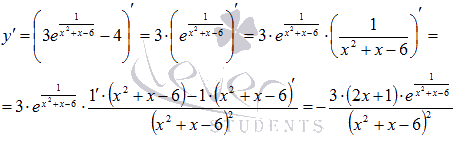
Очевидно, производная существует на всей области определения функции.
Найдем стационарные точки. Производная обращается в ноль при 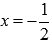 . Эта стационарная точка попадает в интервалы (-3;1] и (-3;2).
. Эта стационарная точка попадает в интервалы (-3;1] и (-3;2).
1. Для первого промежутка  вычисляем значение функции при x=-4 и предел на минус бесконечности:
вычисляем значение функции при x=-4 и предел на минус бесконечности:
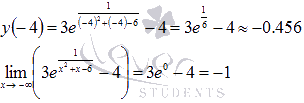
Так как 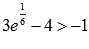 , то
, то 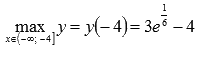 , а о наименьшем значении функции выводов сделать нельзя. Можно лишь утверждать, что значения функции ограничены снизу значением -1 (на минус бесконечности значения функции асимптотически приближаются к прямой y=-1).
, а о наименьшем значении функции выводов сделать нельзя. Можно лишь утверждать, что значения функции ограничены снизу значением -1 (на минус бесконечности значения функции асимптотически приближаются к прямой y=-1).
2. Второй интервал 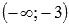 интересен тем, что не содержит ни одной стационарной точки и ни одна из его границ не является строгой. В этом случае мы не сможем найти ни наибольшего, ни наименьшего значения функции. Вычислив предел на минус бесконечности и при стремлении аргумента к минус трем слева, мы лишь сможем определить интервал значений функции:
интересен тем, что не содержит ни одной стационарной точки и ни одна из его границ не является строгой. В этом случае мы не сможем найти ни наибольшего, ни наименьшего значения функции. Вычислив предел на минус бесконечности и при стремлении аргумента к минус трем слева, мы лишь сможем определить интервал значений функции:
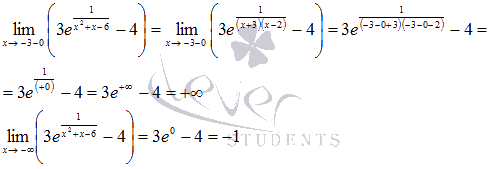
Следовательно, значения функции находятся в интервале  при xиз промежутка
при xиз промежутка 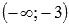 .
.
3. Для третьего промежутка (-3;1] вычислим значение функции в стационарной точке 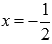 и при x=1, а также односторонний предел, при стремлении аргумента к -3 справа:
и при x=1, а также односторонний предел, при стремлении аргумента к -3 справа:
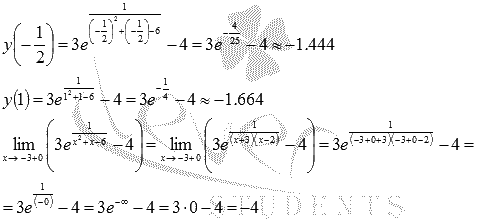
Следовательно, наибольшее значение на этом интервале функция принимает в стационарной точке  , наименьшее значение функции мы вычислить не можем, но значения функции ограничены снизу величиной -4.
, наименьшее значение функции мы вычислить не можем, но значения функции ограничены снизу величиной -4.
4. Для интервала (-3;2) воспользуемся результатами из предыдущего пункта и еще вычислим односторонний предел при стремлении к двойке слева:
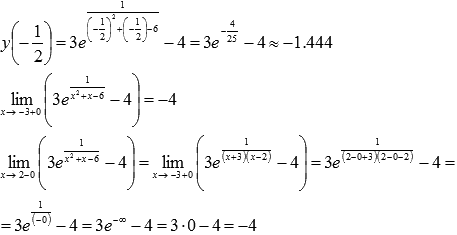
Поэтому 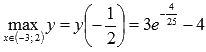 , наименьшее значение определить нет возможности, значения функции ограничены снизу величиной -4.
, наименьшее значение определить нет возможности, значения функции ограничены снизу величиной -4.
5. Результаты предыдущих двух пунктов позволяют утверждать, что на интервале [1;2) наибольшее значение 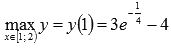 функция принимает при x=1, наименьшее значение найти нельзя, значения функции ограничены снизу величиной -4.
функция принимает при x=1, наименьшее значение найти нельзя, значения функции ограничены снизу величиной -4.
6. На промежутке  функция не достигает ни наибольшего, ни наименьшего значения.
функция не достигает ни наибольшего, ни наименьшего значения.
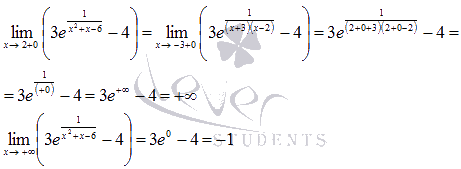
То есть, на этом интервале функция принимает значения из промежутка  .
.
7. Вычислив значение функции при x=4, можно утверждать, что 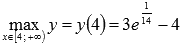 и на плюс бесконечности функция асимптотически приближается к прямой y=-1.
и на плюс бесконечности функция асимптотически приближается к прямой y=-1.
А теперь можно сопоставить полученные в каждом пункте результаты с графиком функции. Синими пунктирными линиями обозначены асимптоты.
Графическая иллюстрация.
Часть графика функции на интервале выпуклости изображена синим цветом, на интервале вогнутости – красным цветом.
Сейчас рассмотрим пример, когда область определения второй производной не совпадает с областью определения функции. В этом случае, как мы уже отмечали, точки области определения, в которых не существует конечная вторая производная, следует включать в интервалы выпуклости и (или) вогнутости.
Пример.
Найти промежутки выпуклости и вогнутости графика функции 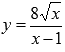 .
.
Решение.
Начнем с области определения функции:
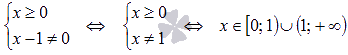
Найдем вторую производную:
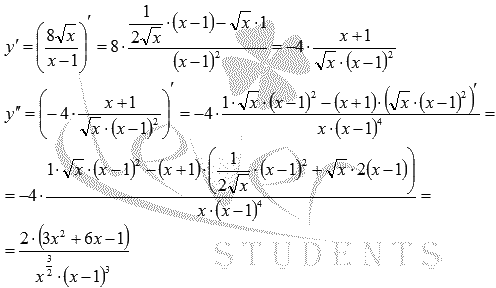
Областью определения второй производной является множество 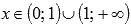 . Как видите, x=0 принадлежит области определения исходной функции, но не принадлежит области определения второй производной. Не забывайте про эту точку, ее нужно будет включить в интервал выпуклости и (или) вогнутости.
. Как видите, x=0 принадлежит области определения исходной функции, но не принадлежит области определения второй производной. Не забывайте про эту точку, ее нужно будет включить в интервал выпуклости и (или) вогнутости.
Теперь решаем неравенства 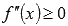 и
и 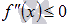 на области определения исходной функции. Применим метод интервалов. Числитель выражения
на области определения исходной функции. Применим метод интервалов. Числитель выражения 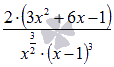 обращается в ноль при
обращается в ноль при 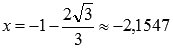 или
или 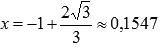 , знаменатель – при x = 0 или x = 1. Схематично наносим эти точки на числовую прямую и выясняем знак выражения на каждом из интервалов, входящих в область определения исходной функции (она показана заштрихованной областью на нижней числовой прямой). При положительном значении ставим знак «плюс», при отрицательном – знак «минус».
, знаменатель – при x = 0 или x = 1. Схематично наносим эти точки на числовую прямую и выясняем знак выражения на каждом из интервалов, входящих в область определения исходной функции (она показана заштрихованной областью на нижней числовой прямой). При положительном значении ставим знак «плюс», при отрицательном – знак «минус».
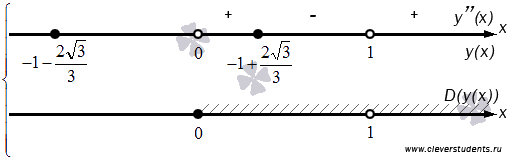
Таким образом,

и

Следовательно, включив точку x=0, получаем ответ.
При  график функции имеет выпуклость направленную вниз, при
график функции имеет выпуклость направленную вниз, при  - выпуклость направленную вверх.
- выпуклость направленную вверх.
Графическая иллюстрация.
Часть графика функции на интервале выпуклости изображена синим цветом, на интервалах вогнутости – красным цветом, черной пунктирной прямой является вертикальная асимптота.
К началу страницы
Графическая иллюстрация.
Часть графика функции на интервале выпуклости изображена синим цветом, на интервалах вогнутости – красным цветом, точки перегиба показаны черными точками.
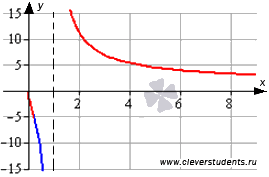
Пример.
Найдите абсциссы всех точек перегиба графика функции 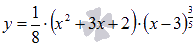 .
.
Решение.
Областью определения данной функции является все множество действительных чисел.
Найдем производную.
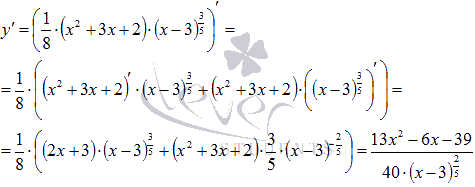
Первая производная, в отличии от исходной функции, не определена при x=3. Но 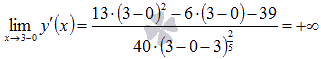 и
и 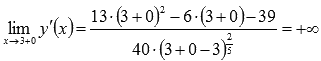 . Следовательно, в точке с абсциссой x=3существует вертикальная касательная к графику исходной функции. Таким образом, x=3 может быть абсциссой точки перегиба графика функции.
. Следовательно, в точке с абсциссой x=3существует вертикальная касательная к графику исходной функции. Таким образом, x=3 может быть абсциссой точки перегиба графика функции.
Находим вторую производную, область ее определения и точки, в которых она обращается в ноль:
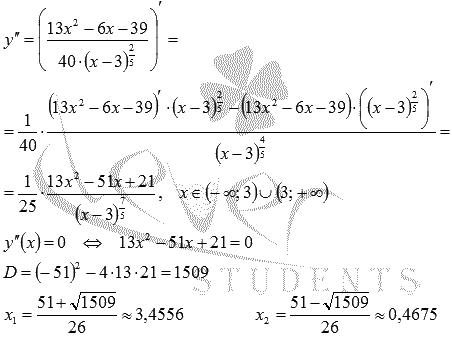
Получили еще две возможные абсциссы точек перегиба. Отмечаем все три точки на числовой прямой и определяем знак второй производной на каждом из полученных интервалов.
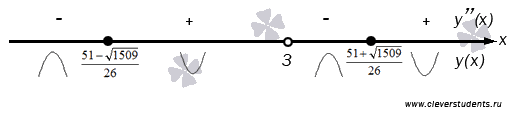
Вторая производная меняет знак, проходя через каждую из точек, следовательно, все они являются абсциссами точек перегиба.
Графическая иллюстрация.
Части графика функции на интервалах выпуклости изображены синим цветом, на интервалах вогнутости – красным цветом, точки перегиба показаны черными точками.
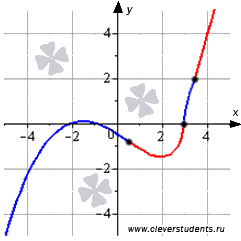
Первое достаточное условие перегиба графика функции позволяет определять точки перегиба и не требуют существования второй производной в них. Поэтому, первое достаточное условие можно считать универсальным и самым используемым.
Сейчас сформулируем еще два достаточных условия перегиба, но они применимы лишь при существовании конечной производной в точке перегиба до некоторого порядка.
Графическая иллюстрация.
Часть графика функции на интервале выпуклости изображена синим цветом, на интервале вогнутости – красным цветом, точка перегиба показана черной точкой.
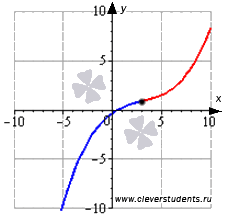
Графическая иллюстрация.
Часть графика функции на интервале выпуклости изображена синим цветом, на интервале вогнутости – красным цветом, точка перегиба показана черной точкой.
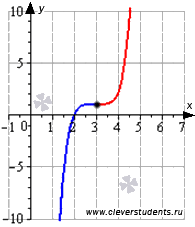
Асимптоты кривой

Прямая называется асимптотой кривой y = f (x), если расстояние от точки М кривой до этой прямой стремится к нулю при удалении точки М вдоль кривой в бесконечность от начала координат (рис. 1.7).
Рис. 1.7
Различают вертикальные и наклонные асимптоты. Вертикальная асимптота имеет уравнение вида x = x0 и является прямой, параллельной оси Оy. Наклонная асимптота имеет уравнение вида y = k x + b. В частном случае при k = 0 асимптота называется горизонтальной, так как ее уравнение y = bесть прямая, параллельная оси Ох.
В  ертикальные асимптоты.
ертикальные асимптоты.
Пусть дана кривая y = f (x). Для нахождения вертикальной асимптоты этой кривой находят точки ее бесконечного разрыва (точки разрыва второго рода).
Если, например,
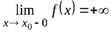 и
и  ,
,
то прямая x = x0 ─ вертикальная асимптота кривой y = f (x) (рис. 1.8).
Наклонные и горизонтальные асимптоты.
Пусть задана кривая y = f (x). Для нахождения наклонной асимптоты, уравнение которой y = k x + b, находят коэффициенты k и b, вычисляя пределы: 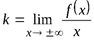 ,
,  . Эти пределы вычисляются отдельно для случаев
. Эти пределы вычисляются отдельно для случаев 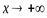 и
и  . Если хотя бы один из пределов для вычисленияk и bравен ∞ или не существует, то кривая наклонных и горизонтальных асимптот не имеет.
. Если хотя бы один из пределов для вычисленияk и bравен ∞ или не существует, то кривая наклонных и горизонтальных асимптот не имеет.
В частном случае, когда k = 0, а b ─ конечное число, кривая имеет горизонтальную асимптоту, уравнение которой y = b.
Пример. Найти асимптоты кривой 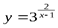 .
.
Решение. Функция 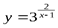 определена на всем множестве действительных чиселR, кроме точки x = 1. Определим характер разрыва, для чего вычислим пределы функции при x → 1 слева (x < 1) и справа (x > 1):
определена на всем множестве действительных чиселR, кроме точки x = 1. Определим характер разрыва, для чего вычислим пределы функции при x → 1 слева (x < 1) и справа (x > 1):
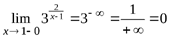 ,
, 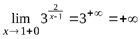 .
.
Так как один из пределов бесконечен, то x = 1 является точкой разрыва второго рода, и, следовательно, кривая имеет вертикальную асимптоту x = 1.
Определим, имеет ли кривая наклонную или горизонтальную асимптоту. Для этого вычисляем соответствующие пределы:
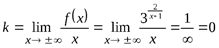
 ,
, 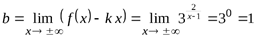 Уравнение асимптотыy = k x + b принимает вид y = 1 (горизонтальная асимптота).
Уравнение асимптотыy = k x + b принимает вид y = 1 (горизонтальная асимптота).
С
Рис. 1.9
хематический график функции представлен на рис. 1.9.
1.14. Схема полного исследования функции и построение ее графика
Литература: [3], гл. V, § 11
[5], Ч.1, гл. 6, § 6.6
1. Находим область определения функции.
2. Устанавливаем четность, нечетность функции, периодичность. Находим характерные точки, например, точки пересечения с осями координат.
3.Находим точки разрыва функции, определяем их характер. При наличии точек разрыва второго рода (точек бесконечного разрыва) устанавливаем наличие вертикальных асимптот графика функции.
4. Находим производную функции, критические точки, промежутки монотонности, точки экстремума и значения функции в этих точках.
5. Находим вторую производную функции, интервалы выпуклости и вогнутости кривой и точки перегиба графика функции.
6.Устанавливаем наличие у исследуемой кривой наклонных и горизонтальных асимптот.
7. По полученным данным строим график функции.
Замечание. Если функция является четной или нечетной, то исследование проводят не на всей числовой оси, а на промежутке [0, +∞). Затем график продолжают симметрично относительно оси ординат на промежуток (-∞, 0), если функция четная, и относительно центра системы координат, если функция нечетная.
Если функция периодическая, то ее график строят для одного периода, а затем периодически продолжают на всю числовую ось.
Пример. Провести полное исследование функции 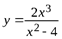 и построить ее график.
и построить ее график.
Решение.
1. Функция определена и непрерывна на всей числовой оси, кроме точек x = ± 2.
2. Функция нечетная, так как для нее выполняется условие 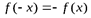 . Поэтому достаточно провести исследование на промежутке [0, +∞).
. Поэтому достаточно провести исследование на промежутке [0, +∞).
3. В промежутке [0, +∞) имеется одна точка разрыва x = 2. Исследуем характер точки разрыва, для чего вычислим следующие пределы:
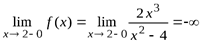 ,
, 
Так как односторонние пределы бесконечные, то прямая x = 2 является вертикальной асимптотой.
4. Находим первую производную:
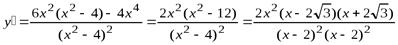 .
.
Находим критические точки на промежутке [0, +∞):  ,
,  . В точке
. В точке 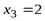 производная не существует, но эта точка не является критической, так как функция в ней не определена.
производная не существует, но эта точка не является критической, так как функция в ней не определена.
5. Находим вторую производную:
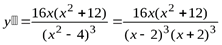 .
.
Вторая производная на промежутке [0, +∞) обращается в ноль в точке x1 = 0 и не существует в точке x3 = 2, которая не входит в область определения функции.
По полученным данным строим таблицу:
| x | 0 | (0, 2) | 2 | (2, 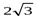 ) )
| 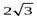
| 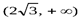
|

| 0 | − | Не существует | – | 0 | + |
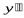
| 0 | − | Не существует | + | + | + |
| y | 0 | 
| Не существует | 
| min
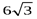
| 
|
В первой строке таблицы указаны интервалы, на которые критические точки и точки, где вторая производная равна нулю или не существует, разбивают промежуток [0, +∞). Во второй строке указан знак первой производной в этих интервалах, в третьей − знак второй производной. В четвертой строке условно изображено возрастание или убывание функции на промежутке (по знаку первой производной), и выпуклость или вогнутость кривой (по знаку второй производной).
6. Ищем наклонную асимптоту:
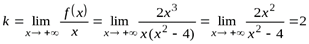 ,
,
 .
.
Кривая на промежутке [0, +∞) имеет наклонную асимптоту 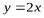 .
.
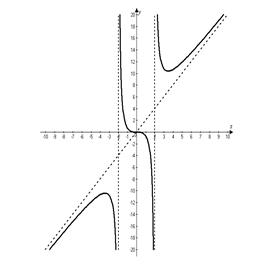
Строим вертикальную x = 2 и наклонную y = 2x асимптоты, а затем по данным таблицы строим график исследуемой функции на промежутке [0, +∞), который затем продолжаем на промежуток (-∞, 0) симметрично относительно центра системы координат.
15. понятие первообразной и неопределенного интеграла таблица неопределенных интегралов

Определение первообразной.
Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство  для любого х из заданного промежутка.
для любого х из заданного промежутка.
Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство 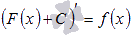 . Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
. Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
Проверка.
Для проверки результата продифференцируем полученное выражение:
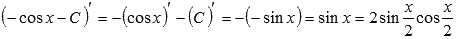
В итоге получили подынтегральную функцию, значит, интегрирование выполнено правильно. В последнем переходе была использована формула синуса двойного угла.
Интегрирование по частям.
Интегрирование по частям основано на представлении подынтегрального выражения в виде произведения 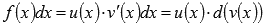 и последующем применении формулы
и последующем применении формулы 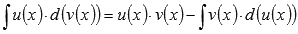 . Этот метод является очень мощным инструментом интегрирования. В зависимости от подынтегральной функции, метод интегрирования по частям иногда приходится применять несколько раз подряд до получения результата. Для примера найдем множество первообразных функции арктангенс.
. Этот метод является очень мощным инструментом интегрирования. В зависимости от подынтегральной функции, метод интегрирования по частям иногда приходится применять несколько раз подряд до получения результата. Для примера найдем множество первообразных функции арктангенс.
Пример.
Вычислить неопределенный интеграл 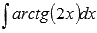 .
.
Решение.
Пусть 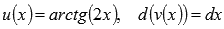 , тогда
, тогда
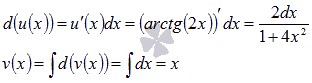
Следует отметить, что при нахождении функции v(x) не прибавляют произвольную постоянную С.
Теперь применяем формулу интегрирования по частям:
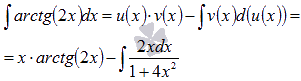
Последний интеграл вычислим по методу подведения под знак дифференциала.
Так как  , то
, то 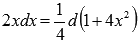 . Поэтому
. Поэтому 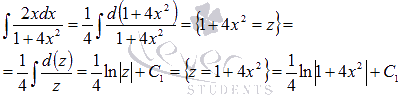
Следовательно,

где 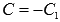 .
.
Ответ:
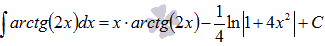 .
.
Основные трудности при интегрировании по частям порождает выбор: какую часть подынтегрального выражения брать за функцию u(x), а какую за дифференциал d(v(x)). Однако существует ряд стандартных рекомендаций, с которыми рекомендуем ознакомиться в разделе интегрирование по частям.
Замечание.
Если функция y = f(x) неположительная на отрезке [a; b], то площадь криволинейной трапеции может быть найдена как 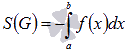 .
.
Пример.
Вычислить площадь фигуры, ограниченной линиями 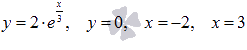 .
.
Решение.
Построим фигуру на плоскости: прямая y = 0 совпадает с осью абсцисс, прямые x = -2 и x = 3 параллельны оси ординат, а кривая 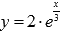 может быть построена с помощью геометрических преобразований графика функции
может быть построена с помощью геометрических преобразований графика функции 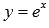 .
.

Таким образом, нам требуется найти площадь криволинейной трапеции. Геометрический смысл определенного интеграла нам указывает на то, что искомая площадь выражается определенным интегралом. Следовательно, 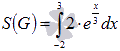 . Этот определенный интеграл можно вычислить по формуле Ньютона-Лейбница:
. Этот определенный интеграл можно вычислить по формуле Ньютона-Лейбница:
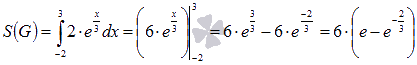
Замечание.
При нахождении площадей криволинейных трапеций совсем не обязательно сначала строить эту фигуру. Если Вы знаете, что функция y = f(x) неотрицательная на отрезке [a; b] (как в нашем примере) или неположительная, то можно сразу применять формулы 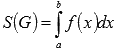 или
или 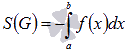 .
.
Пример.
Вычислить площадь фигуры, ограниченной линиями  .
.
Решение.
Построим эту фигуру. Прямая y = 0 совпадает с осью Ox, прямые x = -2 и x = 4параллельны оси Oy, а графиком функции 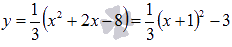 является парабола с вершиной в точке (-1; -3) ветви которой направлены вверх. Найдем точки пересечения этой параболы с осью абсцисс:
является парабола с вершиной в точке (-1; -3) ветви которой направлены вверх. Найдем точки пересечения этой параболы с осью абсцисс:
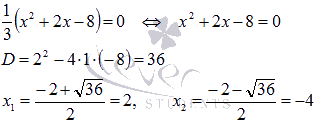
Следовательно, эта парабола пересекает ось абсцисс в точках (-4; 0) и (2; 0).
Таким образом, наша фигура G имеет следующий вид.

Эта фигура не является криволинейной трапецией, так как функция 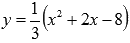 меняет знак на отрезке [-2; 4].
меняет знак на отрезке [-2; 4].
Как же быть в этом случае? Очень просто. Фигуру G можно представить в виде объединения двух криволинейных трапеций 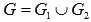 и по свойству аддитивности площади
и по свойству аддитивности площади  .
.
На отрезке [2; 4] график параболы находится в неотрицательной области, поэтому 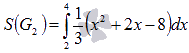 . На отрезке [-2; 2] функция
. На отрезке [-2; 2] функция 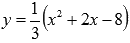 неположительная, следовательно, в силу замечания к геометрическому смыслу определенного интеграла, имеем
неположительная, следовательно, в силу замечания к геометрическому смыслу определенного интеграла, имеем 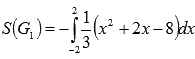 . Осталось вычислить определенные интегралы по формуле Ньютона-Лейбница:
. Осталось вычислить определенные интегралы по формуле Ньютона-Лейбница:
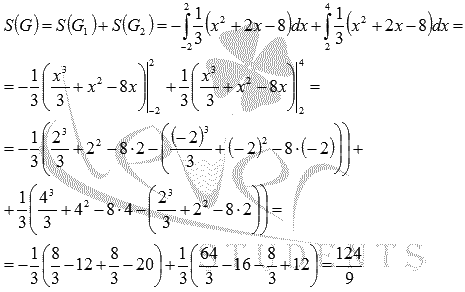
Обратите внимание на то, что нельзя находить площадь этой фигуры как 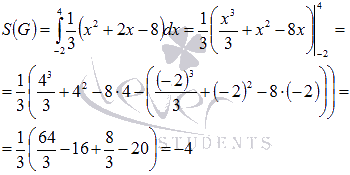 .
.
В нашем примере полученное таким образом значение представляет собой разность 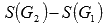 .
.
Фигуры, ограниченные линиями y = c, y = d, x = 0 и x = g(y), где функция x = g(y)непрерывна и не меняет знак на отрезке [c; d], также являются криволинейными трапециями.
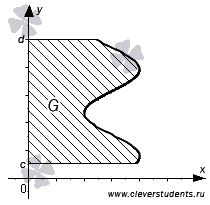
Геометрический смысл определенного интеграла  состоит в том, что его значение равно площади криволинейной трапеции для непрерывной и неотрицательной функции x=g(y) на отрезке [c;d]. Также справедливо
состоит в том, что его значение равно площади криволинейной трапеции для непрерывной и неотрицательной функции x=g(y) на отрезке [c;d]. Также справедливо 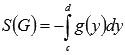 для непрерывной и неположительной функции x=g(y) на отрезке [c;d].
для непрерывной и неположительной функции x=g(y) на отрезке [c;d].
Пример.
Вычислить площадь фигуры, ограниченной осью ординат и линиями 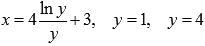 .
.
Решение.
Построить график функции 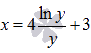 не очень легко. Попробуем обойтись без этого. Эта функция определена для всех положительных значений аргумента y. Оценим значения функции на отрезке [1; 4]. Из свойств основных элементарных функций мы знаем, что функция натурального логарифма является возрастающей на всей своей области определения. Более того, на отрезке [1; 4] она неотрицательна, то есть,
не очень легко. Попробуем обойтись без этого. Эта функция определена для всех положительных значений аргумента y. Оценим значения функции на отрезке [1; 4]. Из свойств основных элементарных функций мы знаем, что функция натурального логарифма является возрастающей на всей своей области определения. Более того, на отрезке [1; 4] она неотрицательна, то есть, 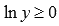 . Выражение
. Выражение  на отрезке [1; 4] также будет неотрицательным, так как знаменатель является положительным числом на этом отрезке. Из этого можно заключить, что функция
на отрезке [1; 4] также будет неотрицательным, так как знаменатель является положительным числом на этом отрезке. Из этого можно заключить, что функция 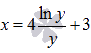 является положительной на интервале [1; 4]. Поэтому фигура в этом примере является криволинейной трапецией, и ее площадь мы будем искать как
является положительной на интервале [1; 4]. Поэтому фигура в этом примере является криволинейной трапецией, и ее площадь мы будем искать как 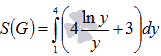 .
.
Осталось вычислить определенный интеграл, для чего найдем одну из первообразных функции 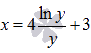 и применим формулу Ньютона-Лейбница:
и применим формулу Ньютона-Лейбница:
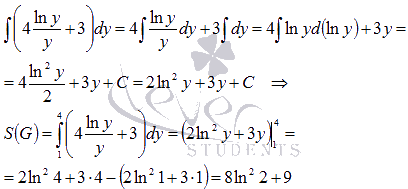
Для наглядности все же приведем чертеж.
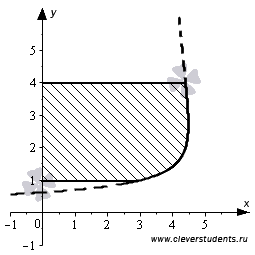
Подведем итог.
Мы выяснили геометрический смысл определенного интеграла и обнаружили его связь с площадью криволинейной трапеции. Таким образом, мы получили возможность находить площади и более сложных фигур, которые можно представить объединением криволинейных трапеций.
Формула Ньютона-Лейбница
Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.
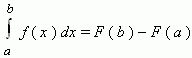
Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x) , вычислить ее значения в точках a и b и найти разность F(b) – F(a).
При выводе формулы интегрирования по частям было получено равенство u dv = d (uv) – v du. Проинтегрировав его в пределах от a до b и учитывая теорему 4 параграфа этой статьи о свойствах определённого интеграла, получим
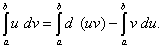
Как это следует из теоремы 2 параграфа о свойствах неопределённого интеграла, первый член в правой части равен разности значений произведения uv при верхнем и нижнем пределах интегрирования. Записав эту разность кратко в виде
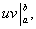
получаем формулу интегрирования по частям для вычисления определенного интеграла:
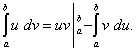 (49)
(49)
Пример 6. Вычислить определённый интеграл
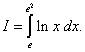
Решение. Интегрируем по частям, полагая u = ln x, dv = dx; тогда du = (1/x)dx, v = x. По формуле (49) находим

Найти определённый интеграл по частям самостоятельно, а затем посмотреть решение
Пример 7. Найти определённый интеграл
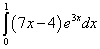 .
.
Правильное решение и ответ.
Пример 8. Найти определённый интеграл
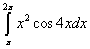 .
.
Правильное решение и ответ.
Перейдём к вычислению определённого интеграла методом замены переменной. пусть

где, по определению, F(x) – первообразная для f(x). Если в подынтегральном выражении произвести замену переменной
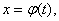
то в соответствии с формулой (16) можно записать
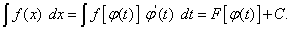
В этом выражении
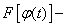
первообразная функция для
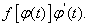
В самом деле, её производная, согласно правилу дифференцирования сложной функции, равна
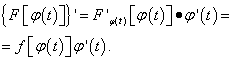
Пусть α и β – значения переменной t , при которых функция
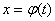
принимает соответственно значения aи b, т.е.
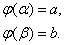
Тогда
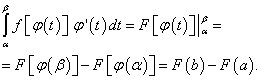
Но, согласно формуле Ньютона-Лейбница, разность F(b) – F(a) есть
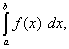
поскольку F(x) – первообразная для f(x).
Итак,
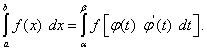 (50)
(50)
Это и есть формула перехода к новой переменной под знаком определённого интеграла. С её помощью определённый интеграл
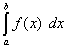
после замены переменной
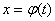
преобразуется в определённый интеграл относительно новой переменной t. При этом старые пределы интегрирования a и b заменяются новыми пределами  и
и  . Чтобы найти новые пределы, нужно в уравнение
. Чтобы найти новые пределы, нужно в уравнение
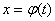
поставить значения x = aи x = b, т.е. решить уравнения
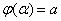
и
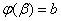
относительно  и
и  . После нахождения новых пределов интегрирования вычисление определённого интеграла сводится к применению формулы Ньютона-Лейбница к интегралу от новой переменной t. В первообразной функции, которая получается в результате нахождения интеграла, возвращаться к старой переменной нет необходимости.
. После нахождения новых пределов интегрирования вычисление определённого интеграла сводится к применению формулы Ньютона-Лейбница к интегралу от новой переменной t. В первообразной функции, которая получается в результате нахождения интеграла, возвращаться к старой переменной нет необходимости.
При вычислении определённого интеграла методом замены переменной часто бывает удобно выражать не старую переменную как функцию новой, а, наоборот, новую – как функцию старой.
Пример 9. Вычислить определённый интеграл
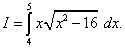
Решение. Произведём замену переменной, полагая
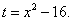
Тогда dt = 2x dx, откуда x dx = (1/2) dt, и подынтегральное выражение преобразуется так:
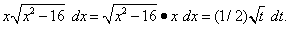
Найдём новые пределы интегрирования. Подстановка значений x = 4 и x = 5 в уравнение
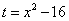
даёт
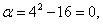
а
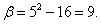
Используя теперь формулу (50), получим

После замены переменной мы не возвращались к старой переменной, а применили формулу Ньютона-Лейбница к полученной первообразной.
Формула Ньютона-Лейбница
Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.
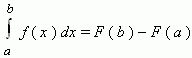
Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x) , вычислить ее значения в точках a и b и найти разность F(b) – F(a).
Примеры решения задач
Пример 1. Найти полный дифференциал функции 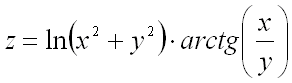 .
.
Решение.
Полным дифференциалом 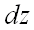 функции
функции 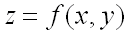 называется линейная (относительно
называется линейная (относительно 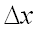 и
и  ) часть полного приращения функции:
) часть полного приращения функции: 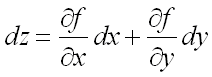 .
.
Следовательно, для выполнения задания достаточно найти частные производные первого порядка от функции и подставить их в вышеприведенную формулу.
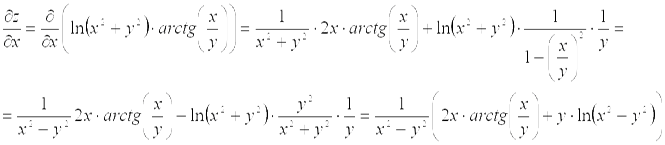
Здесь и ниже использовалось правило дифференцирования произведения двух функций и правило дифференцирования сложной функции одной переменной.
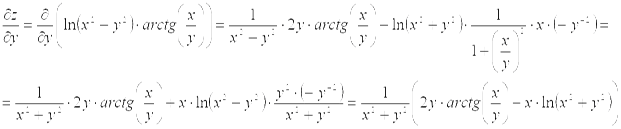
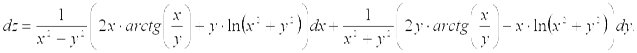
Ответ: 
Пример №1
Найти наибольшее и наименьшее значения функции z=x2+2xy−y2−4x в замкнутой области, ограниченной линиями x=3, y=0 и y=x+1.
Решение
Будем следовать указанному выше алгоритму, но для начала разберёмся с чертежом заданной области, которую обозначим буквой D. Нам заданы уравнения трёх прямых, кои эту область ограничивают. Прямая x=3проходит через точку (3;0) параллельно оси ординат (оси Oy). Прямая y=0 – это уравнение оси абсцисс (оси Ox). Ну, а для построения прямой y=x+1 найдём две точки, через которые и проведём данную прямую. Можно, конечно, подставить вместо x парочку произвольных значений. Например, подставляя x=10, получим: y=x+1=10+1=11. Мы нашли точку (10;11), лежащую на прямой y=x+1. Однако лучше отыщем те точки, в которых прямая y=x+1 пересекается с линиями x=3 и y=0. Почему это лучше? Потому, что мы одним выстрелом уложим пару зайцев: получим две точки для построения прямой y=x+1 и заодно выясним, в каких точках эта прямая пересекает иные линии, ограничивающие заданную область. Прямая y=x+1пересекает прямую x=3 в точке (3;4), а прямую y=0 – в точке (−1;0). Дабы не загромождать ход решения вспомогательными пояснениями, то вопрос о получении этих двух точек вынесу в примечание.
Как были получены точки (3;4) и (−1;0)? показать\скрыть
Всё готово для построения чертежа, который будет иметь такой вид:
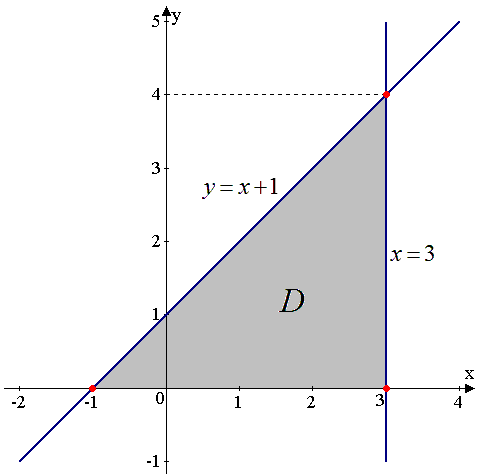
Вот теперь перейдём к первому шагу алгоритма. Найдём частные производные первого порядка:
∂z∂x=2x+2y−4;∂z∂y=2x−2y.
Заметьте, что найденные производные первого порядка существуют для всех значений x и y. Т.е. нету точек, в которых хотя бы одна производная не существует. Попробуем отыскать точки, в которых обе частные производные равны нулю (стационарные точки):
{2x+2y−4=0;2x−2y=0.{x+y=2;x−y=0.
Мы получили систему линейных алгебраических уравнений. Для решения таких систем можно применить, например, метод Крамера. Однако в данном случае можно поступить попроще. Из второго уравнения имеем: y=x. Подставляя y=x в первое уравнение, получим: x+x=2, 2x=2, x=1. Так как x=1, то y=x=1. Итак, (1;1) – единственная стационарная точка функции z.
Однако недостаточно просто найти стационарные точки. Нужно выбрать те из них, которые принадлежат области D. В нашем случае точка (1;1) принадлежит этой области. Обозначим эту точку как M1(1;1). Вычислим значение функции в этой точке:
z1=z(M1)=12+2⋅1⋅1−12−4⋅1=−2.
А почему точка (1;1) принадлежит области D? показать\скрыть
Теперь настал черёд исследовать поведение функции на границе области, т.е. переходим ко второму шагу алгоритма. Начнём с прямой y=0.
Прямая y=0 (ось абсцисс) ограничивает область D при условии −1≤x≤3. Подставим y=0 в заданную функцию z(x,y)=x2+2xy−y2−4x. Полученную в результате подстановки функцию одной переменной x обозначим как f1(x):
f1(x)=z(x,0)=x2+2x⋅0−02−4x=x2−4x.
Теперь для функции f1(x) нужно найти наибольшее и наименьшее значения на отрезке −1≤x≤3. Отыщем производную этой функции и приравняем её к нулю:
f′1(x)=2x−4;2x−4=0;x=2.
Значение x=2 принадлежит отрезку −1≤x≤3, поэтому к списку точек добавим ещё и M2(2;0). Кроме того, вычислим значения функции z на концах отрезка −1≤x≤3, т.е. в точках M3(−1;0) и M4(3;0). Кстати, если бы точка M2 не принадлежала рассматриваемому отрезку, то, разумеется, значение функции z в ней вычислять не было бы надобности.
Итак, вычислим значения функции z в точках M2, M3, M4. Можно, конечно, подставлять координаты данных точек в исходное выражение z=x2+2xy−y2−4x. Например, для точки M2 получим:
z2=z(M2)=22+2⋅2⋅0−02−4⋅2=−4.
Однако вычисления можно немного упростить. Для этого стоит вспомнить, что на отрезке M3M4 имеем z(x,y)=f1(x). Распишу это подробно:
z2=z(M2)=z(2,0)=f1(2)=22−4⋅2=−4;z3=z(M3)=z(−1,0)=f1(−1)=(−1)2−4⋅(−1)=5;z4=z(M4)=z(3,0)=f1(3)=32−4⋅3=−3.
Разумеется, что в столь подробных записях обычно нет нужды, и все вычисления в дальнейшем станем записывать покороче:
z2=f1(2)=22−4⋅2=−4;z3=f1(−1)=(−1)2−4⋅(−1)=5;z4=f1(3)=32−4⋅3=−3.
Теперь обратимся к прямой x=3. Эта прямая ограничивает область D при условии 0≤y≤4. Подставим x=3 в заданную функцию z. В результате такой подстановки мы получим функцию f2(y):
f2(y)=z(3,y)=32+2⋅3⋅y−y2−4⋅3=−y2+6y−3.
Для функции f2(y) нужно найти наибольшее и наименьшее значения на отрезке 0≤y≤4. Отыщем производную этой функции и приравняем её к нулю:
f′2(y)=−2y+6;−2y+6=0;y=3.
Значение y=3 принадлежит отрезку 0≤y≤4, поэтому к найденным ранее точкам добавим ещё и M5(3;3). Кроме того, нужно вычислить значение функции z в точках на концах отрезка 0≤y≤4, т.е. в точках M4(3;0) и M6(3;4). В точке M4(3;0) мы уже вычисляли значение z. Вычислим значение функции z в точках M5 и M6. Напомню, что на отрезке M4M6 имеем z(x,y)=f2(y), поэтому:
z5=f2(3)=−32+6⋅3−3=6;z6=f2(4)=−42+6⋅4−3=5.
И, наконец, рассмотрим последнюю границу области D, т.е. прямую y=x+1. Эта прямая ограничивает область D при условии −1≤x≤3. Подставляя y=x+1 в функцию z, будем иметь:
f3(x)=z(x,x+1)=x2+2x⋅(x+1)−(x+1)2−4x=2x2−4x−1.
Вновь мы получили функцию одной переменной x. И вновь нужно найти наибольшее и наименьшее значения этой функции на отрезке −1≤x≤3. Отыщем производную функции f3(x) и приравняем её к нулю:
f′3(x)=4x−4;4x−4=0;x=1.
Значение x=1 принадлежит отрезку −1≤x≤3. Если x=1, то y=x+1=2. Добавим к списку точек ещё и M7(1;2) и выясним, чему равно значение функции z в этой точке. Точки на концах отрезка −1≤x≤3, т.е. точки M3(−1;0) и M6(3;4), были рассмотрены ранее, значение функции в них мы уже находили.
z7=f3(1)=2⋅12−4⋅1−1=−3.
Второй шаг решения закончен. Мы получили семь значений:
z1=−2;z2=−4;z3=5;z4=−3;z5=6;z6=5;z7=−3.
Обратимся к третьему шагу алгоритма. Выбирая наибольшее и наименьшее значения из тех чисел, что были получены в третьем пункте, будем иметь:
zmin=−4;zmax=6.
Задача решена, осталось лишь записать ответ.
Ответ: zmin=−4;zmax=6.
Примеры нахождения производной по направлению
Пример 1. Найти производную функции 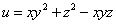 в точке M0(1; 2; 3) по направлению вектора
в точке M0(1; 2; 3) по направлению вектора 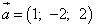 .
.
Решение. Найдём частные производные функции в точке M0:

Найдём направляющие косинусы, пользуясь определением скалярного произведения векторов:
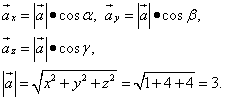
Следовательно,
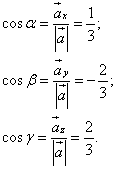
Теперь можем найти производную по направлению данной функции по её формуле:
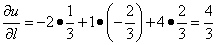
Нет времени вникать в решение? Можно заказать работу!
А сейчас - домашнее задание. В нём дана функция не трёх, а лишь двух переменных, но несколько иначе задан направляющий вектор. Так что придётся вновь повторить векторную алгебру.
Пример 2. Найти производную функции 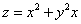 в точке M0(1; 2) по направлению вектора
в точке M0(1; 2) по направлению вектора 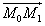 , где M1 - точка с координатами (3; 0).
, где M1 - точка с координатами (3; 0).
Посмотреть правильное решение и ответ.
Вектор, задающий направление производной, может быть дан и в такой форме, как в следующем примере - в виде разложения по ортам координатных осей, но эта хорошо знакомая тема из самого начала векторной алгебры.
Пример 3. Найти производную функции 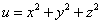 в точке M0(1; 1; 1) по направлению вектора
в точке M0(1; 1; 1) по направлению вектора 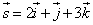 .
.
Решение. Найдём направляющие косинусы вектора
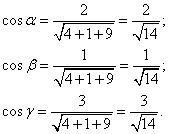
Найдём частные производные функции в точке M0:
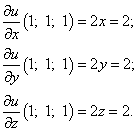
Следовательно, можем найти производную по направлению данной функции по её формуле:
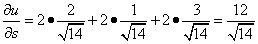 .
.
Градиент функции
Градиент функции нескольких переменных в точке M0 характеризует направление максимального роста этой функции в точке M0 и величину этого максимального роста.
Как найти градиент?
Нужно определить вектор, проекциями которого на оси координат являются значения частных производных 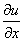 ,
,  ,
, 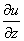 этой функции в соответствующей точке:
этой функции в соответствующей точке:
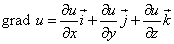 .
.
То есть, должно получиться представление вектора по ортам координатных осей, в котором на каждый орт умножается соответствующая его оси частная производная.
Для градиента функции двух переменных формула короче:
 .
.
Пример 4. Найти градиент функции 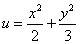 в точке M0(2; 4;).
в точке M0(2; 4;).
Решение. Найдём частные производные функции в точке M0:

Следовательно, можем записать искомый градиент данной функции:
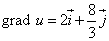 .
.
Площадь плоской фигуры
Если f (x,y) = 1 в интеграле 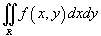 , то двойной интеграл равен площади области интегрирования R.
, то двойной интеграл равен площади области интегрирования R.
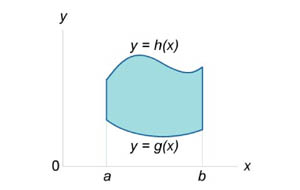
Площадь области типа I (элементарной относительно оси Оy) (рисунок 1) выражается через повторный интеграл в виде
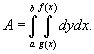
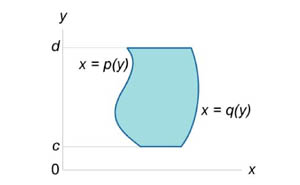
Аналогично, площадь области типа II (элементарной относительно оси Оx) (рисунок 2) описывается формулой
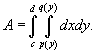
| 
| |
| Рис.1 | Рис.2 |
Объем тела
Если f (x,y) > 0 в области интегрирования R, то объем цилиндрического тела с основанием R, ограниченного сверху поверхностью z = f (x,y), выражается формулой
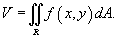
В случае, когда R является областью типа I, ограниченной линиями 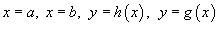 , объем тела равен
, объем тела равен
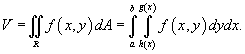
Для области R типа II, ограниченной графиками функций 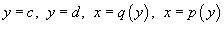 , объем соответственно равен
, объем соответственно равен

Если в области R выполняется неравенство 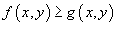 , то объем цилиндрического тела между поверхностями z1 = f (x,y) и z2 = g (x,y) с основанием R равен
, то объем цилиндрического тела между поверхностями z1 = f (x,y) и z2 = g (x,y) с основанием R равен

Площадь поверхности
Предположим, что поверхность задана функцией z = f (x,y), имеющей область определения R. Тогда площадь такой поверхности над областью z определяется формулой
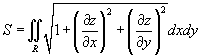
при условии, что частные производные 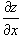 и
и 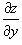 непрерывны всюду в области R.
непрерывны всюду в области R.
Пример
Вычислить площадь области R, ограниченной линиями  .
.
Решение.
Сначала определим точки пересечения двух заданных линий.
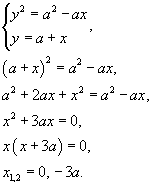
Следовательно, координаты точек пересечения равны

Область R представлена на рисунке 5 выше. Будем рассматривать ее как область типа II. Для вычисления площади преобразуем уравнения границ:
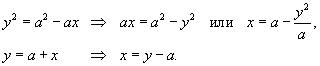
Получаем
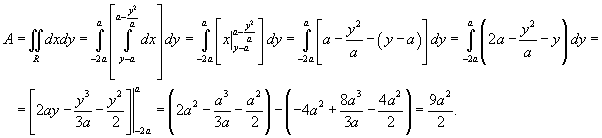
Моменты инерции пластины
Момент инерции пластины относительно оси Ox выражается формулой
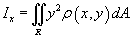
Аналогично вычисляется момент инерции пластины относительно оси Oy :
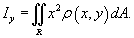
Полярный момент инерции пластины равен
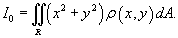
Заряд пластины
Предположим, что электрический заряд распределен по области R в плоскости Oxy и его плотность распределения задана функцией 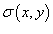 . Тогда полный заряд пластины Q определяется выражением
. Тогда полный заряд пластины Q определяется выражением

Среднее значение функции
Приведем также формулу дял расчета среднего значения некоторой распределенной величины. Пусть f (x,y) является непрерывной функцией в замкнутой области R в плоскости Oxy. Среднее значение функции μ функции f (x,y) в области R определяется формулой
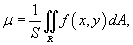
где  − площадь области интегрирования R.
− площадь области интегрирования R.
Пример
Вычислить моменты инерции треугольника, ограниченного прямыми 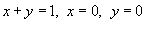 (рисунок 2) и имеющего плотность
(рисунок 2) и имеющего плотность  .
.
Решение.
Найдем момент инерции пластины относительно оси Ox.
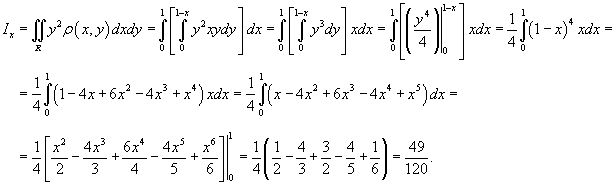
Аналогично вычислим момент инерции относительно оси Oy.
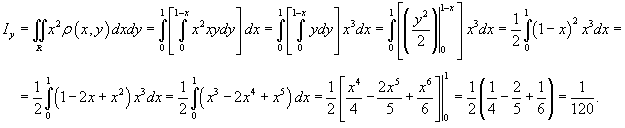
Длина кривой
Пусть C является гладкой, кусочно-непрерывной кривой, которая описывается вектором 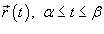 . Длина данной кривой выражается следующим криволинейным интегралом
. Длина данной кривой выражается следующим криволинейным интегралом
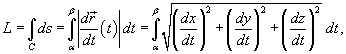
где 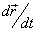 − производная, а
− производная, а 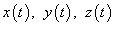 − компоненты векторной функции
− компоненты векторной функции 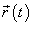 .
.
Если кривая C задана в плоскости, то ее длина выражается формулой
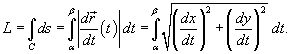
Если кривая C представляет собой график заданной явно, непрерывной и дифференцируемой функции 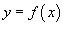 в плоскости Oxy, то длина такой кривой вычисляется по формуле
в плоскости Oxy, то длина такой кривой вычисляется по формуле
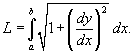
Наконец, если кривая C задана в полярных координатах уравнением 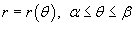 , и функция
, и функция  является непрерывной и дифференцируемой в интервале
является непрерывной и дифференцируемой в интервале 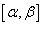 , то длина кривой определяется выражением
, то длина кривой определяется выражением
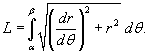
Масса кривой
Предположим, что кусок проволоки описывается некоторой пространственной кривой C. Пусть масса распределена вдоль этой кривой с плотностью ρ (x,y,z). Тогда общая масса кривой выражается через криволинейный интеграл первого рода
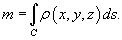
Если кривая C задана в параметрическом виде с помощью векторной функции 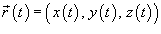 , то ее масса описывается формулой
, то ее масса описывается формулой
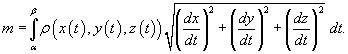
В случае плоской кривой, заданной в плоскости Oxy, масса определяется как
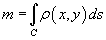
или в параметрической форме
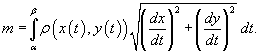
Работа поля
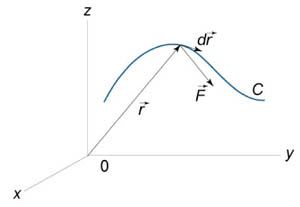
Работа при перемещении тела в силовом поле  вдоль кривой C выражается через криволинейный интеграл второго рода
вдоль кривой C выражается через криволинейный интеграл второго рода
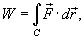
где  − сила, действующая на тело,
− сила, действующая на тело,  − единичный касательный вектор (рисунок 1). Обозначение
− единичный касательный вектор (рисунок 1). Обозначение  означает скалярное произведение векторов
означает скалярное произведение векторов  и
и  .
.
Заметим, что силовое поле  не обязательно является причиной движения тела. Тело может двигаться под действием другой силы. В таком случае работа силы
не обязательно является причиной движения тела. Тело может двигаться под действием другой силы. В таком случае работа силы  иногда может оказаться отрицательной.
иногда может оказаться отрицательной.
Если векторное поля задано в координатной форме в виде
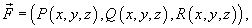
то работа поля вычисляется по формуле
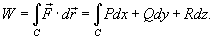
В частном случае, когда тело двигается вдоль плоской кривой C в плоскости Oxy, справедлива формула
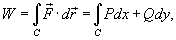
Где 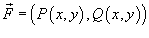
Если траектория движения C определена через параметр t (t часто означает время), то формула для вычисления работы принимает вид
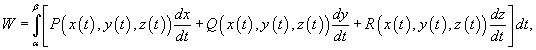
где t изменяется в интервале от α до β. Если векторное поле  потенциально, то работа по перемещению тела из точки A в точку B выражается формулой
потенциально, то работа по перемещению тела из точки A в точку B выражается формулой
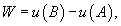 где
где  − потенциал поля.
− потенциал поля.
| 
| |
| Рис.1 | Рис.2 |
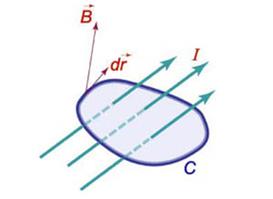
Закон Ампера
Криволинейный интеграл от магнитного поля с индукцией  вдоль замкнутого контура C пропорционален полному току, протекающему через область, ограниченную контуром C (рисунок 2). Это выражается формулой
вдоль замкнутого контура C пропорционален полному току, протекающему через область, ограниченную контуром C (рисунок 2). Это выражается формулой

где 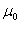 - магнитная проницаемость ваккуума, равная
- магнитная проницаемость ваккуума, равная 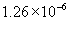 Н/м.
Н/м.
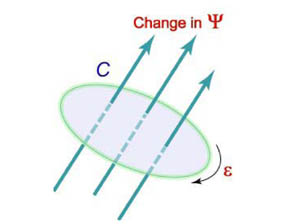
Закон Фарадея
Электродвижущая сила ε, наведенная в замкнутом контуре C, равна скорости изменения магнитного потока ψ, проходящего через данный контур (рисунок 3).
|
| Рис.3 |

Пример
Определить массу проволоки, имеющей форму отрезка от точки A(1,1) до B(2,4). Масса распределена вдоль отрезка с плотностью 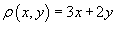 .
.
Решение. Составим сначала параметрическое уравнение прямой AB. 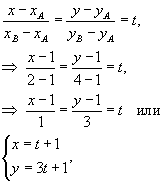
где параметр t изменяется в интервале [0,1]. Тогда масса проволоки равна
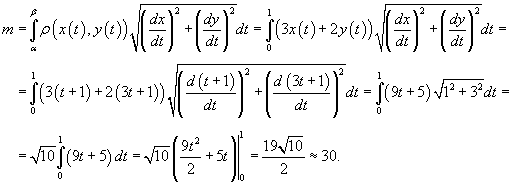
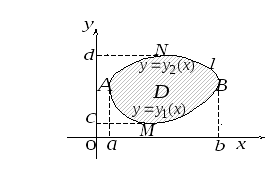
Формула грина
Формула Грина устанавливает связь между двойным интегралом по области  и криволинейным интегралом по контуру
и криволинейным интегралом по контуру  , ограничивающему эту область. Будем считать, что область
, ограничивающему эту область. Будем считать, что область 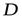 является стандартной в направлении каждой координатной оси и снизу ограничена графиком функции
является стандартной в направлении каждой координатной оси и снизу ограничена графиком функции 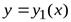 (дугой
(дугой  ), сверху — графиком функции
), сверху — графиком функции 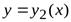 (дугой
(дугой  ), которые вместе составляют замкнутый контур
), которые вместе составляют замкнутый контур  .
.
Пусть в области  и на ее границе
и на ее границе  заданы функции
заданы функции 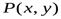 и
и 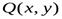 непрерывные вместе со своими частными производными
непрерывные вместе со своими частными производными 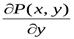 ,
, 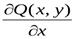 ,тогда
,тогда
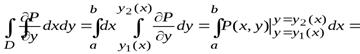
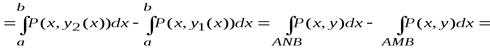
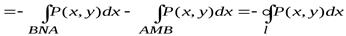 ,
,
где обход контура  совершается в положительном направлении, т. е. против часовой стрелки (область
совершается в положительном направлении, т. е. против часовой стрелки (область 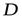 остается слева). Следовательно,
остается слева). Следовательно,
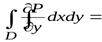
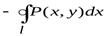 . (1)
. (1)
Аналогично получаем
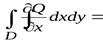
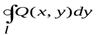 , (2)
, (2)
где обход контура 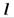 также совершается в положительном направлении.
также совершается в положительном направлении.
Вычитая почленно (1) из (2), получаем формулу Грина
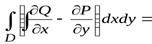
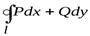 .
.
Замечание 1.Если обход контура 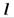 совершается в отрицательном направлении, т. е. по часовой стрелке (область
совершается в отрицательном направлении, т. е. по часовой стрелке (область 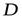 остается справа), то формула Грина принимает вид
остается справа), то формула Грина принимает вид
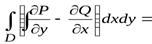
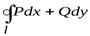 .
.
Замечание 2.Формула Грина дает возможность вычислять площадь области с помощью криволинейного интеграла. Действительно, если 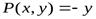 ,
, 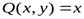 , то формула Грина перепишется так:
, то формула Грина перепишется так:
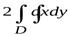
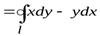 ,
,
откуда
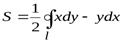 , (3)
, (3)
где обход контура  совершается против часовой стрелки.
совершается против часовой стрелки.
Пример. Определить с помощью криволинейного интеграла площадь, ограниченную эллипсом с полуосями  и
и  .
.
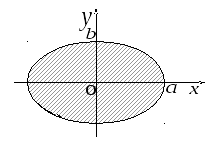
Решение.Запишем параметрические уравнения эллипса
 .
.
Тогда
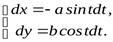
И по формуле (3) получим
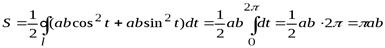 .
.
Теорема 1
Для того, чтобы интеграл ∫AB∪Pdx+Qdy∫AB∪Pdx+Qdy не зависел от формы пути, соединяющего точки A A и B B , необходимо и достаточно, чтобы интеграл по любому замкнутому контуру был равен нулю.
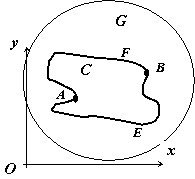
Доказательство
Необходимость . Пусть C=AEBFA∪C=AEBFA∪ - произвольный замкнутый контур, лежащий в области GG, A A и B B - произвольные точки этого контура.
Так как, по условию, ∫AEB∪Pdx+Qdy=∫AFB∪Pdx+Qdy∫AEB∪Pdx+Qdy=∫AFB∪Pdx+Qdy, то ∫AEB∪Pdx+Qdy=−∫BFA∪Pdx+Qdy⇒∫AEB∪Pdx+Qdy+∫BFA∪Pdx+Qdy=0⇒∮СPdx+Qdy=0∫AEB∪Pdx+Qdy=−∫BFA∪Pdx+Qdy⇒∫AEB∪Pdx+Qdy+∫BFA∪Pdx+Qdy=0⇒∮СPdx+Qdy=0.
Достаточность . Пусть для любого контура C⊂GC⊂G выполняется ∮CPdx+Qdy=0∮CPdx+Qdy=0. Пусть ∀A∈G∀A∈G, ∀B∈G∀B∈G - произвольные точки, AEB∪AEB∪ и AFB∪AFB∪ - две различных кривых, соединяющих эти точки. AEBFA∪AEBFA∪ - замкнутый контур, поэтому ∮AEBFA∪Pdx+Qdy=0⇒∮AEB∪Pdx+Qdy++∮BFA∪Pdx+Qdy=0⇒∮AEB∪Pdx+Qdy−∮AFB∪Pdx+Qdy=0⇒∫AEB∪Pdx+Qdy=∫AFB∪Pdx+Qdy∮AEBFA∪Pdx+Qdy=0⇒∮AEB∪Pdx+Qdy++∮BFA∪Pdx+Qdy=0⇒∮AEB∪Pdx+Qdy−∮AFB∪Pdx+Qdy=0⇒∫AEB∪Pdx+Qdy=∫AFB∪Pdx+Qdy,
что и требовалось доказать.
Теорема 2
Для того, чтобы интеграл ∮CPdx+Qdy∮CPdx+Qdy по любому контуру C C был равен нулю, необходимо и достаточно, чтобы функции P,QP,Q и их частные производные были непрерывны, и выполнялось условие ∂Q∂x=∂P∂y∂Q∂x=∂P∂y.
Доказательство
Необходимость . От противного. Пусть для ∀C⊂G∀C⊂G выполняется ∮CPdx+Qdy=0∮CPdx+Qdy=0, но существует точка M0∈GM0∈G такая, что (∂Q∂x−∂P∂y)(M0)≠0(∂Q∂x−∂P∂y)(M0)≠0.
Предположим для определённости, что (∂Q∂x−∂P∂y)(M0)=s>0(∂Q∂x−∂P∂y)(M0)=s>0. Так как разность ∂Q∂x−∂P∂y∂Q∂x−∂P∂y непрерывна, существует окрестность точки M0M0 такая, что (∂Q∂x−∂P∂y)>s/2(∂Q∂x−∂P∂y)>s/2.
Выберем контур C C , целиком лежащий в этой окрестности. Если D D - область ограниченная этим контуром, то, по формуле Грина, ∮СP(x,y)dx+Q(x,y)dy=∬D(∂Q∂x−∂P∂y)dxdy∮СP(x,y)dx+Q(x,y)dy=∬D(∂Q∂x−∂P∂y)dxdy.
Но, по теореме об интегрировании неравенств, ∬D(∂Q∂x−∂P∂y)dxdy>s2⋅S(D)>0∬D(∂Q∂x−∂P∂y)dxdy>s2⋅S(D)>0 { S(D)S(D) - площадь области D D } , т.е. ∮CPdx+Qdy>0∮CPdx+Qdy>0, что противоречит условиям теоремы. Следовательно, в любой точке M0∈GM0∈G выполняется условие ∂Q∂x=∂P∂y∂Q∂x=∂P∂y.
Достаточность . Если в любой точке M0∈GM0∈G выполняется условие ∂Q∂x=∂P∂y∂Q∂x=∂P∂y, то для любого контура C C
∮CP(x,y)dx+Q(x,y)dy=∬D(∂Q∂x−∂P∂y)dxdy=0∮CP(x,y)dx+Q(x,y)dy=∬D(∂Q∂x−∂P∂y)dxdy=0 { D D - область ограниченная контуром C C } .
Таким образом, для того, чтобы криволинейный интеграл ∫AB∪Pdx+Qdy∫AB∪Pdx+Qdy не зависел от формы пути, соединяющего начальную и конечную точки { или, что то же самое, интеграл по любому замкнутому контуру был равен нулю } , требуется выполнение двух условий:
- Контур и ограниченная им область лежат в некоторой односвязной области, в которой
- P,QP,Q и их частные производные непрерывны и ∂Q∂x=∂P∂y∂Q∂x=∂P∂y.
Отметим существенность первого условия. Так, для интеграла ∫AB∪ydx−xdyx2+y2∫AB∪ydx−xdyx2+y2 второе условие выполняется: ∂Q∂x=∂P∂y=x2−y2(x2+y2)2∂Q∂x=∂P∂y=x2−y2(x2+y2)2, в то же время интеграл по окружности радиуса R R не равен нулю: ∫x2+y2=R2ydx−xdyx2+y2=∣∣∣x=Rcost,y=Rsint0⩽t⩽2π∣∣∣=−∫02π(sin2t+cos2t)dt=−2π∫x2+y2=R2ydx−xdyx2+y2=|x=Rcost,y=Rsint0⩽t⩽2π|=−∫02π(sin2t+cos2t)dt=−2π
Причина - функции P P и Q Q непрерывны всюду, кроме начала координат; удаление точки из плоскости лишает её свойства односвязности.
решение систем линейных уравнений методом гаусса
Понятие метода Гаусса
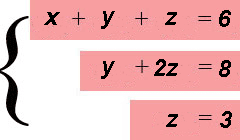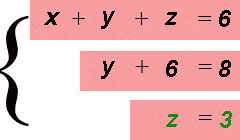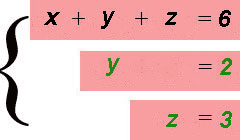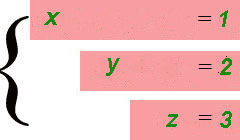
Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в следующем. При помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной (то же самое, что треугольной или ступенчатой) или близкой к трапециевидной (прямой ход метода Гаусса, далее - просто прямой ход). Пример такой системы и её решения - на рисунке сверху.
В такой системе последнее уравнение содержит только одну переменную и её значение можно однозначно найти. Затем значение этой переменной подставляют в предыдущее уравнение (обратный ход метода Гаусса, далее - просто обратный ход), из которого находят предыдущую переменную, и так далее.
В трапециевидной (треугольной) системе, как видим, третье уравнение уже не содержит переменных y и x, а второе уравнение - переменной x.
После того, как матрица системы приняла трапециевидную форму, уже не представляет труда разобраться в вопросе о совместности системы, определить число решений и найти сами решения.
Преимущества метода:
- при решении систем линейных уравнений с числом уравнений и неизвестных более трёх метод Гаусса не такой громоздкий, как метод Крамера, поскольку при решении методом Гаусса необходимо меньше вычислений;
- методом Гаусса можно решать неопределённые системы линейных уравнений, то есть, имеющие общее решение (и мы разберём их на этом уроке), а, используя метод Крамера, можно лишь констатировать, что система неопределённа;
- можно решать системы линейных уравнений, в которых число неизвестных не равно числу уравнений (также разберём их на этом уроке);
- метод основан на элементарных (школьных) методах - методе подстановки неизвестных и методе сложения уравнений, которых мы коснулись в соответствующей статье.
Кроме того, метод Гаусса является основой одного из методов нахождения обратной матрицы.
Чтобы все прониклись простотой, с которой решаются трапециевидные (треугольные, ступенчатые) системы линейных уравнений, приведём решение такой системы с применением обратного хода. Быстрое решение этой системы было показано на картинке в начале урока.
Пример 1. Решить систему линейных уравнений, применяя обратный ход:
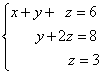
Решение. В данной трапециевидной системе переменная z однозначно находится из третьего уравнения. Подставляем её значение во второе уравнение и получаем значение переменой y:
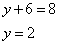
Теперь нам известны значения уже двух переменных - z и y. Подставляем их в первое уравнение и получаем значение переменной x:

Из предыдущих шагов выписываем решение системы уравнений:
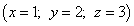
Чтобы получить такую трапециевидную систему линейных уравнений, которую мы решили очень просто, требуется применять прямой ход, связанный с элементарными преобразованиями системы линейных уравнений. Это также не очень сложно.
Пример 3. Решить систему линейных уравнений методом Гаусса:
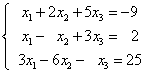
Решение. Подвергаем преобразованиям расширенную матрицу системы:
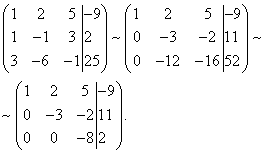
Таким образом, приходим к следующей системе уравнений:
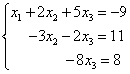
Эта система имеет единственное решение:
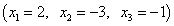
Дата: 2019-03-05, просмотров: 448.